6.16: Difracción de rayos X y reglas de selección

Difracción de rayos X

La última vez discutimos cómo generar\(\mathrm{x}\) -rayos; ahora, hablemos de una aplicación que juega un papel importante en la caracterización de materiales. La difracción de rayos X es una herramienta que nos permite sondear la estructura cristalina de una muestra. Vamos a recorrer el proceso:

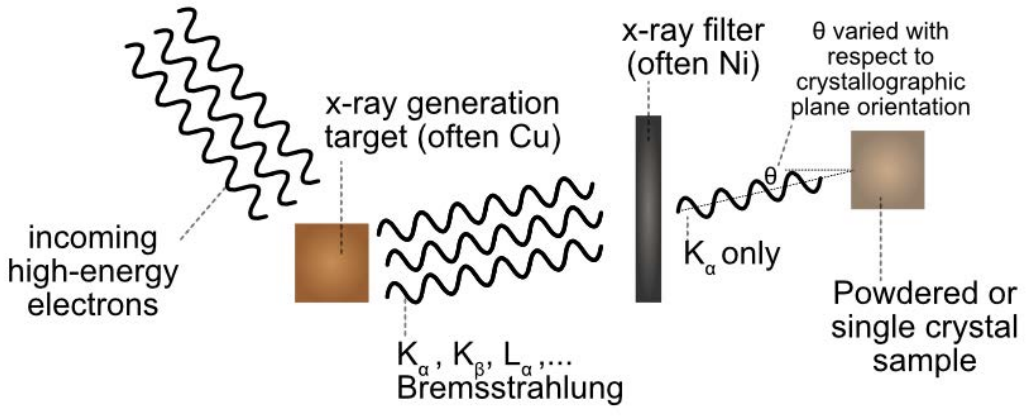
Primero, necesitamos generar\(\mathrm{x}\) -rays: este proceso se muestra a la izquierda. Como discutimos, al disparar electrones de alta energía a un objetivo hecho de átomos pesados (el cobre es una elección común), se generan tanto\(\mathrm{x}\) rayos característicos como Bremsstrahlung. Luego, bombardeando una muestra desconocida con los\(\mathrm{x}\) rayos, y midiendo la luz dispersada en función del ángulo incidente, podemos sondear el espaciamiento interplanar que existe dentro del cristal. Sin embargo, recordemos que la condición de Bragg depende de la longitud de onda: para hacer esto realmente de manera efectiva, solo queremos mantener una banda estrecha de longitudes de onda. Esto se logra empleando un filtro, eliminando todo excepto los\(\mathrm{K}_{\alpha}\)\(\mathrm{x}\) -rayos, por ejemplo.

Después de todo eso, lo que realmente se mide en un experimento de XRD es la intensidad\(\mathrm{x}\) de los rayos dispersos en función del ángulo incidente. Un espectro XRD típico se ve así:

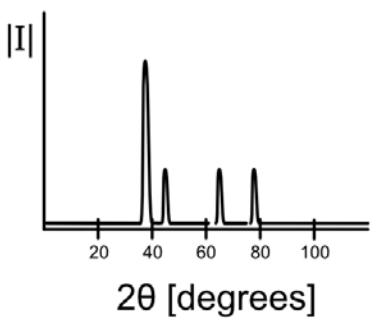
Aquí se representa la intensidad/recuentos\(\mathrm{x}\) de rayos en un detector en función de\(2\theta\), o el doble del ángulo incidente. Es útil utilizar la siguiente tabla para traducir una gráfica XRD a una estructura/elemento de cristal:

\ (\ begin {array} {c|c|c|c|c|c|c}
\ texto {pico #} & 2\ theta &\ theta &\ sin ^2\ theta &\ texto {normalizado} &\ texto {entero} &\ texto {plano}
\\ hline &\ texto {de} &\ fila izquierda\ veces\ dfrac {1} {2} &\ texto {calculadora} &\ texto { dividir todo} &\ texto {multiplicar} &\\
&\ texto {gráfico} & & &\ fila izquierda\ texto {por} &\ fila izquierda\ texto {por} & h^2+k^2+l^2=\
& & & & &\ begin {array} {c}
\\ fila izquierda\
\ texto {más pequeño de}\\
\ text {un entero}
\ end {array} &\ text {(a menudo} 2\ text {o} 3\ text {)} &\ left tarrow
\ end {array}\)

Reglas de selección

Como discutimos en la conferencia, podemos aplicar reglas de selección para determinar qué tipo de estructura cristalina tiene una muestra. Para cada una de las celosías de Bravais, las reglas de selección nos dicen qué planos tienen dispersión coherente y cuáles no:

Cristal cúbico	Planos permitidos (\(\mathrm{hkl}\))	Aviones prohibidos (\(\mathrm{hkl}\))
\(\mathrm{SC}\)	\ (\ mathrm {hkl}\)) ">cualquier\(\mathrm{h,k,l}\)	\ (\ mathrm {hkl}\)) ">ninguno
\(\mathrm{BCC}\)	\ (\ mathrm {hkl}\)) "> número\(\mathrm{h}+\mathrm{k}+\mathrm{l} = \) par	\ (\ mathrm {hkl}\)) "> número\(\mathrm{h}+\mathrm{k}+\mathrm{l} = \) impar
\(\mathrm{FCC}\)	\ (\ mathrm {hkl}\)) "> \(\mathrm{h,k,l}\)todo incluso \(\mathrm{h,k,l}\)todo impar	\ (\ mathrm {hkl}\)) ">\(\mathrm{h,k,l}\) mixto par e impar

Ejemplo: Utilice el siguiente espectro XRD para determinar el elemento que se investigó. Es\(\mathrm{BCC}\) o bien\(\mathrm{FCC}\). Se utilizó\(K_{\alpha}\) radiación de cobre, la cual tiene una longitud de onda de 1.54 Angstroms.

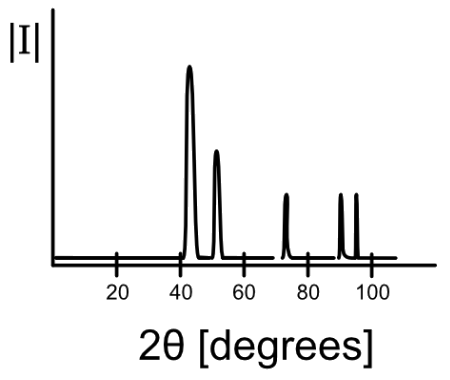
\ (\ begin {array} {c|c}
\ text {Peak #} & 2\ theta\\ hline
\ hline\ hline 1 & 44.51\\
2 & 51.90\\
3 & 76.45\\
4 & 93.02\\
5 & 98.50
\ end {array}\)

Se nos da una gráfica y los valores de\(2\theta\), así que a continuación construyamos el gráfico como se describió anteriormente. Se dan las dos primeras columnas, y podemos calcular rápidamente las dos siguientes:

\ (\ begin {array} {c|c|c|c|c|c}
\ text {pico #} & 2\ theta &\ theta &\ theta &\ sin ^2\ theta &\ texto {normalizado} &\ texto {entero} &\ texto {plano}\
\ hline 1 & 44.51 & 22.25 & 0.1434 & & & & &\
2 & 51.90 & 25.95 & amp; 0.1915 & & & &\
3 & 76.45 & 38.23 & 0.3829 & & & & & &\
4 & 93.02 & 46.51 & 0.5263 & & & & &\
5 & 98.50 & 49.25 & 0.5739 & & & & &
\ end {matriz}\)

Para la siguiente columna, valores normalizados, simplemente dividimos todos los valores en la\(\sin ^2 \theta\) columna por el\(s m a l l e s t\) valor en la\(\sin ^2 \theta\) columna,\(0.1434\).

\ (\ begin {array} {c|c|c|c|c|c|c}
\ texto {pico #} & 2\ theta &\ theta &\ sin ^2\ theta &\ texto {normalizado} &\ texto {entero} &\ texto {plano}\
\ hline 1 & 44.51 & 22.25 & 0.1434 & 1 & & &\\
2 & 51.90 & 25.95 & amp; 0.1915 & 1.33 & &\\
3 & 76.45 & 38.23 & 0.3829 & 2.66 & & &\\
4 & 93.02 & 46.51 & 0.5263 & 3.65 & &\\
5 & 98.50 & 49.25 & 0.5739 & 4 & &
\ end {array}\)

Al observar los valores en la columna normalizada, parecen ser aproximadamente factores de\(\frac{1}{3}\). Para crear enteros, intentemos multiplicar cada uno por 3.

\ (\ begin {array} {c|c|c|c|c|c|c}
\ texto {pico #} & 2\ theta &\ theta &\ sin ^2\ theta &\ texto {normalizado} &\ texto {entero} &\ texto {plano}\
\ hline 1 & 44.51 & 22.25 & 0.1434 & 1 & 3 &\\
2 & 51.90 & 25.95 & 0.1915 & 1.33 & 4 &\\
3 & 76.45 & 38.23 & 0.3829 & 2.66 & 8 &\\
4 & 93.02 & 46.51 & 0.5263 & 3.65 & 11 &\\
5 & 98.50 & 49.25 & 0.5739 & 4 & 12 &
\ end {array}\)

Genial, ¡esto creó enteros! Los enteros en esta columna deben ser la suma de\(h^2, k^2\), y\(l^2\) que forman un plano particular. Intentemos emparejar algunos aviones:

\ (\ begin {array} {c|c|c|c|c|c|c}
\ texto {pico #} & 2\ theta &\ theta &\ sin ^2\ theta &\ texto {normalizado} &\ texto {entero} &\ texto {plano}\
\ hline 1 & 44.51 & 22.25 & 0.1434 & 1 & 3 & (111)\\
2 & 51.90 & 25.95 & 0.1915 & 1.33 & 4 & (200)\\
3 & 76.45 & 38.23 & 0.3829 & 2.66 & 8 & (220)\\
4 & 93.02 & 46.51 & 0.5263 & 3.65 & 11 & (311)\\
5 & 98.50 & 49.25 & 0.5739 & 4 & 12 & (222)
\ end {array}\)

Se necesita un poco de tiempo para desarrollar la intuición en cuanto a cómo combinar los cuadrados de tres números para formar enteros, pero viene con la práctica. Por ahora, puedes verificar que estos (\(\mathrm{hkl}\)) planos realmente generan los enteros en la columna vecina. También tenga en cuenta que cualquier miembro de una familia plana podría generar el entero en cuestión: ¡está bien elegir cualquier plano dentro de esa familia! Por ejemplo, los planos (200), (020) y (002) satisfacen todos\(h^2+k^2+l^2=4\), por lo que cualquiera funcionaría allí.

A continuación, debemos revisar las reglas de selección. Vemos que para cada uno de los planos, los valores de\(\mathrm{h}, \mathrm{k}\), y\(\mathrm{l}\) son todos impares o todos pares. Además el plano (111) está prohibido para los cristales de BCC, ya que\(1+1+1=3\), lo cual es impar. ¡Podemos concluir que esta debe ser una estructura FCC!

Por último, tenemos que averiguar qué elemento FCC es. Podemos combinar algunos viejos principios para resolver esto. Sabemos que la condición de Bragg es

\(\lambda=2 d_{h k l} \sin \theta\)

donde\(\theta\) corresponde a uno de los picos anteriores, que significan interferencia constructiva. Recordemos también que el espaciado interplanar viene dado por

\(d_{h k l}=\dfrac{a}{\sqrt{h^2+k^2+l^2}}\)

Al enchufar una de las entradas de la tabla anterior, podemos averiguar cuál es la constante de celosía. Vamos a usar\(\theta=25.95\) grados y el plano (200):

\ begin {reunió}
a=d_ {h k l}\ sqrt {h^2+k^2+l^2}\\
a=\ dfrac {\ lambda} {2\ sin\ theta}\ sqrt {h^2+k^2+l^2}\\
a=\ dfrac {1.54\ AA} {2 *\ sin\ izquierda (25.95^ {\ circ} derecha)}\ sqrt {2^2+0^2+0^2} =3.52\ AA
\ end {reunidos}

Mirando la tabla periódica, ¡un elemento FCC con parámetro de celosía alrededor\(3.52 \AA\) es níquel!