1.3: Las Formas de las Moléculas (Teoría VSEPR) e Hibridación Orbital

La teoría de la repulsión de pares de electrones de concha de valencia (VSEPR) es una forma sencilla y útil de predecir y racionalizar las formas de las moléculas. La teoría se basa en la idea de minimizar la repulsión electrostática entre pares de electrones, como propuso por primera vez Sidgwick y Powell en 1940, ^[9] luego se generalizó por Gillespie y Nyholm en 1957, ^[10] y luego se aplicó ampliamente a lo largo de los 50 años intermedios. ^[11]

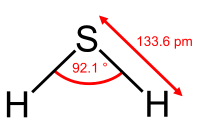
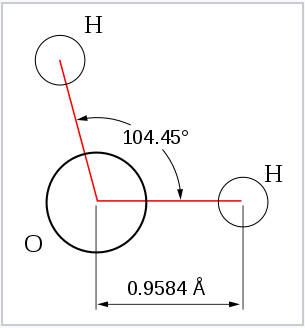
Geometría de la molécula de agua

Para usar el modelo VSEPR, se inicia con la imagen de puntos de Lewis para determinar el número de pares solitarios y dominios de unión alrededor de un átomo central. Debido a que VSEPR considera todos los dominios de enlace por igual (es decir, un enlace sencillo, un doble enlace y un medio enlace todos cuentan como un dominio de electrones), se puede usar una estructura octeto o hipervalente, siempre que el número de pares solitarios (que debería ser el mismo en ambos) se calcule correctamente. Por ejemplo, ya sea en la estructura hipervalente u octeto del ion I ₃ ^- anterior, hay tres pares solitarios en el átomo I central y dos dominios de enlace. Luego seguimos estos pasos para obtener la geometría electrónica:

• Determinar el número de pares solitarios en el átomo central en la molécula y agregar el número de átomos unidos (también conocido como dominios de enlace)
• Este número (el número estérico) define la forma electrónica de la molécula minimizando la repulsión. Por ejemplo, un número estérico de tres da una forma electrónica plana trigonal.
• Los ángulos entre dominios de electrones están determinados principalmente por la geometría electrónica (por ejemplo, 109.5° para un número estérico de 4, lo que implica que la forma electrónica es un tetraedro)
• Estos ángulos son ajustados por la jerarquía de repulsiones: (par solitario - par solitario) > (par solitario - enlace) > (enlace - enlace)

La geometría molecular se deduce de la geometría electrónica considerando que los pares solitarios están presentes pero invisibles. Los métodos más utilizados para determinar la estructura molecular (difracción de rayos X, difracción de neutrones y difracción de electrones) tienen dificultades para ver pares solitarios, pero pueden determinar con precisión la longitud de los enlaces entre los átomos y los ángulos de enlace.

La siguiente tabla da ejemplos de formas electrónicas y moleculares para números estéricos entre 2 y 9. La mayoría de las veces nos preocupan las moléculas que tienen números estéricos entre 2 y 6.

Pares de electrones de unión	Pares solitarios	Dominios de electrones (Steric #)	Forma	Ángulo de unión ideal (ángulo de unión de ejemplo)	Ejemplo	Imagen
2	0	2	lineal	180°	CO 2
3	0	3	plano trigonal	120°	BF 3
2	1	3	doblada	120° (119°)	SO 2
4	0	4	tetraédrico	109.5°	CH 4
3	1	4	piramidal trigonal	109.5° (107°)	NH 3
2	2	4	doblada	109.5° (104.5°)	H 2 O
5	0	5	bipiramidal trigonal	90°, 120°, 180°	PCl 5
4	1	5	oscilación	180°, 120°, 90° (173.1°, 101.6°)	SF 4
3	2	5	En forma de T	90°, 180° (87.5°, < 180°)	CLF 3
2	3	5	lineal	180°	XeF 2
6	0	6	octaédrico	90°, 180°	SF 6
5	1	6	cuadrado piramidal	90° (84.8°), 180°	BrF 5
4	2	6	plano cuadrado	90°, 180°	XeF 4
7	0	7	pentagonal bipiramidal	90°, 72°, 180°	SI 7
6	1	7	piramidal pentagonal	72°, 90°, 144°	XeoF 5 ^−
5	2	7	pentagonal plano	72°, 144°	XeF 5 ^−
8	0	8	antiprismático cuadrado		xEF 8 ^2−
9	0	9	Trigonal Trigonal Trimatic		ReH 9 ^2−

De la Tabla, vemos que algunas de las moléculas mostradas como ejemplos tienen ángulos de unión que se apartan de la geometría electrónica ideal. Por ejemplo, el ángulo de enlace H-N-H en amoníaco es 107°, y el ángulo H-O-H en agua es 104.5°. Esto lo podemos racionalizar en términos de la última regla anterior. El par solitario en amoníaco repele los electrones en los enlaces N-H más de lo que se repelen entre sí. Esta repulsión de pares solitarios ejerce una influencia aún más estérica en el caso del agua, donde hay dos pares solitarios. De manera similar, el ángulo axial F-S-F en la molécula de “balanceo” SF ₄ es de unos pocos grados menos de 180° debido a la repulsión del par solitario en la molécula.

Isómeros geométricos

Para algunas moléculas de la Tabla, observamos que hay más de una forma posible que satisfaga las reglas VSEPR. Por ejemplo, la molécula xEF ₂ tiene un número estérico de cinco y una geometría bipiramidal trigonal. Existen tres posibles estereoisómeros: uno en el que los átomos F ocupan sitios axiales, dando como resultado una molécula lineal, uno en el que los átomos F ocupan un sitio ecuatorial y otro axial (dando como resultado un ángulo de enlace de 90°), y uno en el que los átomos F están ambos en sitios ecuatoriales, con un ángulo de enlace F-Xe-F de 120°.

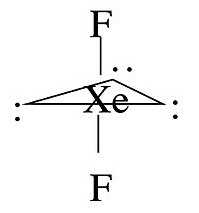
La geometría observada de xEF ₂ es lineal, la cual puede racionalizarse considerando los orbitales que se utilizan para hacer enlaces (o pares solitarios) en las posiciones axial y ecuatorial. Hay cuatro orbitales disponibles, s, p _x, p _y, y p _z. Si elegimos el eje z como dirección axial, podemos ver que los orbitales p _x y p _y se encuentran en el plano ecuatorial. Suponemos que el orbital esférico s es compartido equitativamente por los cinco dominios de electrones de la molécula, los dos enlaces axiales comparten el orbital _pz y los tres enlaces ecuatoriales comparten los orbitales p _{x y p y}. Luego podemos calcular los órdenes de enlace a los átomos F axiales y ecuatoriales de la siguiente manera:

\(axial: \: \frac{1}{5} + \frac{1}{2}p_{z} = 0.7 \: bond (formal \: charge = -0.3)\)

\(equatorial: \: \frac{1}{5}s + \frac{1}{3} p_{x} + \frac{1}{3} p_{y} = 0.867 \:bond (formal \: charge = -0.122)\)

Debido a que el flúor es más electronegativo que un par solitario, prefiere el sitio axial donde tendrá una carga formal más negativa. En general, por este razonamiento, los pares solitarios y los ligandos electropositivos como CH ₃ siempre preferirán los sitios ecuatoriales en la geometría bipiramidal trigonal. Los ligandos electronegativos como el F siempre irán a los sitios axiales.

En el caso del anión BrF ₄ ^-, que es isoelectrónico con xEF ₄ en la Tabla, la geometría electrónica es octaédrica y hay dos posibles isómeros en los que los dos pares solitarios son cis o trans entre sí. En este caso, la repulsión de par solitario - par solitario domina y obtenemos la disposición trans de pares solitarios, dando una geometría molecular plana cuadrada.

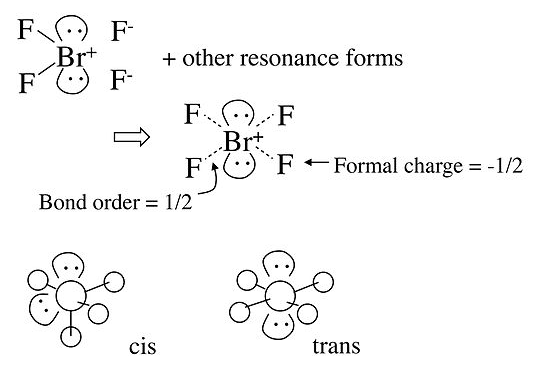
Hibridación orbital

La observación de moléculas en las diversas formas electrónicas mostradas anteriormente está, al principio, en conflicto con nuestra imagen de orbitales atómicos. Para un átomo como el oxígeno, sabemos que el orbital 2s es esférico, y que los orbitales 2p _x, 2p _y, y 2p _z tienen forma de mancuerna y apuntan a lo largo de los ejes cartesianos. La molécula de agua contiene dos átomos de hidrógeno unidos al oxígeno no en un ángulo de 90°, sino en un ángulo de 104.5°. Dadas las orientaciones relativas de los orbitales atómicos, ¿cómo llegamos a ángulos entre dominios de electrones de 104.5°, 120°, y así sucesivamente? Para entender esto necesitaremos aprender un poco sobre la mecánica cuántica de los electrones en átomos y moléculas.

Los orbitales atómicos ψ representan soluciones a la ecuación de onda de Schrödinger,

\[E \psi = \hat{H} \psi\]

Aquí E es la energía de un electrón en la órbita, y\(\hat{H}\) es el operador hamiltoniano.

Por analogía con la mecánica clásica, el hamiltoniano se expresa comúnmente como la suma de operadores correspondientes a las energías cinéticas y potenciales de un sistema en la forma

\[\hat{H} = \hat{T} + \hat{V}\]

dónde\( \hat{V} = V(\mathbf{r} , t)\) está la energía potencial, y

\[ \hat{T} = \frac{\mathbf{\hat{p} \cdot \hat{p}}}{2m} = \frac{\hat{p}^{2}}{2m}= -\frac{\hbar ^{2}}{2m} \nabla ^{2} ,\]

es el operador de energía cinética en el que m es la masa de la partícula y el operador de impulso es:

\[ \hat{p} = -i \mathbf{\hbar} \nabla , \textrm{where} \nabla = \frac{\delta}{\delta x} + \frac{\delta}{\delta y} + \frac{\delta}{\delta z}\]

Aquí\(\mathbf{\hbar}\) está h/2π, donde h es la constante de Planck, y el operador laplaciano ² es:

\[ \nabla^{2} = \frac{\delta ^{2}}{\delta x^{2}} + \frac{\delta ^{2}}{\delta y^{2}} + \frac{\delta ^{2}}{\delta z^{2}}\]

Aunque esta no es la definición técnica del hamiltoniano en la mecánica clásica, es la forma que más comúnmente toma en la mecánica cuántica. Combinando estos juntos produce la forma familiar utilizada en la ecuación de Schrödinger:

\[\hat{H} = \hat{T} + \hat{V} = \frac{\mathbf{\hat{p} \cdot \hat{p}}}{2m} + V(\mathbf{r}, t) = - \frac{\mathbf{\hbar ^{2}}}{2m}\nabla^{2} + V(\mathbf{r}, t)\]

Para átomos similares a hidrógeno (un electrón), la ecuación de Schrödinger se puede escribir como:

\[E \psi = -\frac{\mathbf{\hbar ^ {2}}}{2\mu} \nabla^{2} \psi - \frac{Ze^{2}}{4\pi \epsilon_{0}r} \psi\]

donde Z es la carga nuclear, e es la carga de electrones, y r es la posición del electrón. El término potencial radial en el lado derecho de la ecuación se debe a la interacción Coulomb, es decir, la atracción electrostática entre el núcleo y el electrón, en la que ε ₀ es la constante dieléctrica (permitividad del espacio libre) y

\[ \mu = \frac{m_{e}m_{n}}{m_{e} + m_{n}}\]

es la masa reducida de 2 cuerpos del núcleo de masa m _n y el electrón de masa m _e. A una buena aproximación, µ ≈ m _e.

Erwin Schrödinger como joven científico

Esta es la ecuación que Erwin Schrödinger derivó en 1926 para resolver para las energías y formas de los orbitales atómicos s, p, d y f en átomos similares a hidrógeno. Fue un enorme salto conceptual tanto para la física como para la química porque no sólo explicaba los niveles de energía cuantificados del átomo de hidrógeno, sino que también proporcionaba la base teórica para la regla del octeto y la disposición de los elementos en la tabla periódica.

La ecuación de Schrödinger se puede utilizar para describir sistemas químicos que son más complicados que el átomo de hidrógeno (por ejemplo, átomos de múltiples electrones, moléculas, cristales infinitos y la dinámica de esos sistemas) si sustituimos la función energética potencial apropiada V (r, t) por la hamiltoniana. La matemática se vuelve más complicada y la ecuación debe resolverse numéricamente en esos casos, así que para nuestros propósitos nos quedaremos con el caso más simple de átomos invariantes en el tiempo, de un electrón, similares a hidrógeno.

Sin entrar en demasiados detalles sobre la ecuación de Schrödinger, podemos señalar algunas de sus propiedades más importantes:

\[E \psi = -\frac{\mathbf{\hbar ^ {2}}}{2\mu} \nabla^{2} \psi - \frac{Ze^{2}}{4\pi \epsilon_{0}r} \psi\]

• La ecuación deriva del hecho de que la energía total (E) es la suma de la energía cinética (KE) y la energía potencial (PE). Estas tres cantidades se representan matemáticamente como operadores en la ecuación.
• En el lado izquierdo de la ecuación, el operador de energía total (E) es un escalar que se multiplica por la función wavefunction ψ. ψ es una función de las coordenadas espaciales (x, y, z) y está relacionado con la probabilidad de que el electrón esté en ese punto en el espacio.
• El primer término en el lado derecho de la ecuación representa la energía cinética (KE). El operador de energía cinética es proporcional a ² (el operador Laplaciano) que toma la segunda derivada (con respecto a tres coordenadas espaciales) de ψ. Así, la ecuación de Schrödinger es una ecuación diferencial.
• El segundo término en el lado derecho de la ecuación representa el potencial Coulomb (PE), es decir, la energía atractiva entre el núcleo cargado positivamente y el electrón cargado negativamente.
• Las soluciones a la ecuación de Schrödinger son un conjunto de energías E (que son cantidades escalares) y ondulaciones (también conocidas como orbitales atómicos) ψ, que son funciones de las coordenadas espaciales. A veces verá las energías referidas como valores propios y los orbitales como funciones propias, porque matemáticamente la ecuación de Schrödinger es una ecuación de función propia - valor propio. Aunque ψ es una función de las coordenadas, E no lo es. Entonces un electrón en un orbital de 2p _z tiene la misma energía total E (= PE + KE) sin importar dónde se encuentre en el espacio.
• Estos valores E y sus funciones de onda asociadas ψ se catalogan de acuerdo con sus números cuánticos n, l y m _l. Es decir, hay muchas soluciones a la ecuación diferencial, y cada solución (ψ (xyz) y E) tiene un conjunto único de números cuánticos. Algunos conjuntos de orbitales son degenerados, lo que significa que tienen la misma energía (por ejemplo, 2p _x, 2p _y y 2p _z).
• _{Las soluciones ψ (xyz) a la ecuación de Schrödinger (por ejemplo, los orbitales 1s, 2s, 2p x, 2p y y 2p z) representan amplitudes de probabilidad para encontrar el electrón en un punto particular (x, y, z) en el espacio.} Una amplitud de probabilidad puede tener signo + o -. Por lo general, representamos los diferentes signos mediante sombreado o por signos + y - en los dos lóbulos de una órbita 2p.
• El cuadrado de la amplitud de probabilidad, ψ ², es siempre un número positivo y representa la probabilidad de encontrar el electrón en un punto x, y, z en el espacio. Debido a que la probabilidad total de encontrar el electrón en alguna parte es 1, la función de onda debe normalizarse para que la integral de ψ ² sobre las coordenadas espaciales (de -∞ a +∞) sea 1.
• Las soluciones a la ecuación de Schrödinger son ortogonales, lo que significa que el producto de cualquiera de dos (integrado en todo el espacio) es cero. Por ejemplo, el producto de los orbitales 2s y 2p _x, integrados sobre las coordenadas espaciales de -∞ a +∞, es cero.

Las formas de los primeros cinco orbitales atómicos: 1s, 2s, 2p x, 2p y, y 2p z. Los colores denotan el signo de la función de onda.

La hibridación orbital implica hacer combinaciones lineales de los orbitales atómicos que son soluciones a la ecuación de Schrödinger. Matemáticamente, esto se justifica al reconocer que la ecuación de Schrödinger es una ecuación diferencial lineal. Como tal, cualquier suma de soluciones a la ecuación de Schrödinger también es una solución válida. Sin embargo, seguimos imponiendo la restricción de que nuestros orbitales híbridos deben ser ortogonales y normalizados.

Reglas para la hibridación orbital:

• Sumar y restar orbitales atómicos para obtener orbitales híbridos.
• Sacamos el mismo número de orbitales que colocamos.
• La energía de un orbital híbrido es el promedio ponderado de los orbitales atómicos que lo componen.
• Los coeficientes están determinados por las restricciones de que los orbitales híbridos deben ser ortogonales y normalizados.

Para la hibridación sp, como en la molécula BeF _{2 o CO 2}, hacemos dos combinaciones lineales de los orbitales 2s y 2p _z (asignando z como eje del enlace Be-F):

\[ \psi_{1} = \frac{1}{\sqrt{2}}(2s) + \frac{1}{\sqrt{2}}(2p_{z})\]

\[ \psi_{2} = \frac{1}{\sqrt{2}}(2s) - \frac{1}{\sqrt{2}}(2p_{z})\]

Aquí simplemente hemos sumado y restado los orbitales 2s y 2pz; lo dejamos como un ejercicio para que el estudiante interesado demuestre que ambos orbitales están normalizados (i.e.,\(\int \psi_{1}^{2} d\tau = \int \psi_{2}^{2}d\tau = 1\)) y ortogonales (i.e.,\( \int \psi_{1} \psi_{2} d \tau =0\)).

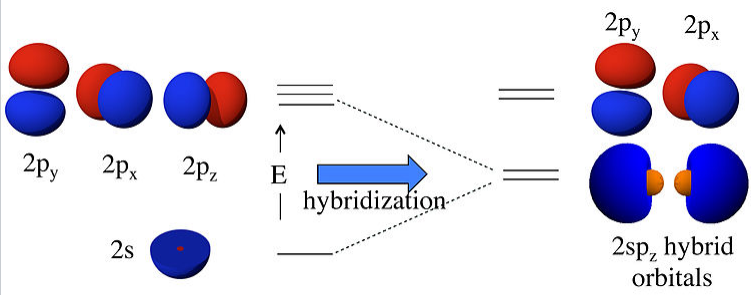
Lo que esto significa físicamente se explica en la siguiente figura. Al combinar los orbitales 2s y 2p _z hemos creado dos nuevos orbitales con grandes lóbulos (alta probabilidad de electrones) apuntando a lo largo del eje z. Estos dos orbitales son degenerados y tienen una energía que está a medio camino entre la energía de los orbitales 2s y 2p _z.

Las combinaciones lineales de los orbitales atómicos 2s y 2p z forman dos híbridos de 2sp z. Los orbitales 2p x y 2p y permanecen inalterados.

Para un átomo de Be aislado, que tiene dos electrones de valencia, el estado de energía más bajo tendría dos electrones emparejados por espín en el orbital 2s. Sin embargo, estos electrones no estarían disponibles para la unión. Al promover estos electrones a los orbitales híbridos degenerados de 2sp _z, se desaparean y se preparan para unirse a los átomos F en BeF ₂. Esto ocurrirá si la energía de vinculación (en el estado promovido) excede a la energía de promoción. La energía de unión global, es decir, la energía liberada al combinar un átomo Be en su estado fundamental con dos átomos F, es la diferencia entre las energías de enlace y promoción.

De manera similar podemos construir híbridos sp ² (por ejemplo, para la molécula BF ₃ o el anión ^NO ₃) a partir de un orbitales atómicos 2s y dos 2p. Tomando el plano de la molécula como plano xy, obtenemos tres orbitales híbridos a 120° entre sí. Los tres híbridos son:

\[\psi_{1} = \frac{1}{\sqrt{3}}(2s) + \frac{\sqrt{2}}{\sqrt{3}}(2p_{x})\]

\[\psi_{2}= \frac{1}{\sqrt{3}}(2s) - \frac{1}{\sqrt{6}}(2p_{x}) + \frac{1}{\sqrt{2}}(2p_{y})\]

\[\psi_{3}= \frac{1}{\sqrt{3}}(2s) - \frac{1}{\sqrt{6}}(2p_{x}) -\frac{1}{\sqrt{2}}(2p_{y})\]

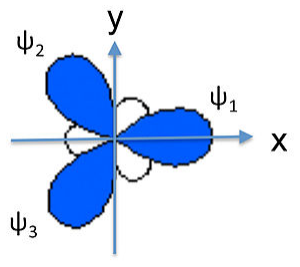
Estos orbitales vuelven a ser degenerados y su energía es el promedio ponderado de las energías de los orbitales atómicos 2s, 2p _x, _{y 2p y}.

Finalmente, para hacer un híbrido sp ³, como en CH ₄, H ₂ O, etc., combinamos los cuatro orbitales atómicos para hacer cuatro híbridos degenerados:

\[\psi_{1} = \frac{1}{2}(2s + 2p_{x} + 2p_{y} + 2p_{z})\]

\[\psi_{2} = \frac{1}{2}(2s - 2p_{x} - 2p_{y} + 2p_{z})\]

\[\psi_{3} = \frac{1}{2}(2s + 2p_{x} - 2p_{y} - 2p_{z})\]

\[\psi_{4} = \frac{1}{2}(2s - 2p_{x} + 2p_{y} - 2p_{z})\]

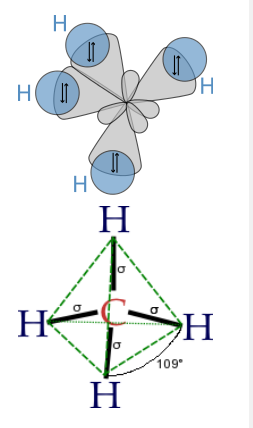
Los lóbulos de los orbitales híbridos sp ³ apuntan hacia los vértices de un tetraedro (o esquinas alternas de un cubo), consistentes con el ángulo de enlace tetraédrico en CH ₄ y los ángulos casi tetraédricos en NH ₃ y H ₂ O. De igual manera, podemos demostrar que podemos construir la forma electrónica bipiramidal trigonal haciendo híbridos sp y sp ², y la geometría octaédrica a partir de tres conjuntos de híbridos sp. El cuadro que surge de esto es que los orbitales atómicos pueden hibridarse según lo requiera la forma que mejor minimice las repulsiones de pares de electrones.

Curiosamente, sin embargo, los ángulos de enlace en PH ₃, H ₂ S y H ₂ Se están cerca de 90°, lo que sugiere que P, S y Se utilizan principalmente sus orbitales p para unirse a H en estas moléculas. Esto es consistente con el hecho de que la diferencia de energía entre los orbitales s y p se mantiene aproximadamente constante bajando por la tabla periódica, pero la energía del enlace disminuye a medida que los electrones de valencia se alejan más lejos del núcleo. En los compuestos de elementos en las filas 3, 4 y 5 de la tabla periódica, existe una tendencia decreciente a utilizar híbridos orbitales s-p en la unión. Para estos elementos más pesados, la energía de unión no es suficiente para compensar la energía necesaria para promover los electrones s a orbitales híbridos s-p.