2.11: Cadenas y anillos de sistemas conjugados con π

Etileno: El sistema π es análogo al enlace σen H ₂

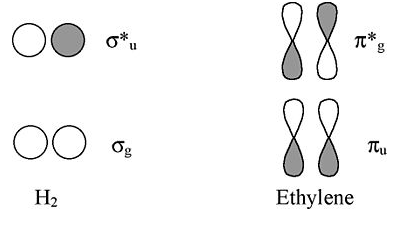
Vistos desde arriba o abajo, los orbitales π de etileno se parecen a los orbitales H ₂ σ. Así podemos mapear soluciones de cadenas y anillos de átomos de H a cadenas y anillos de orbitales π-orbitales (como hicimos para el caso de tres orbitales de O ₃).

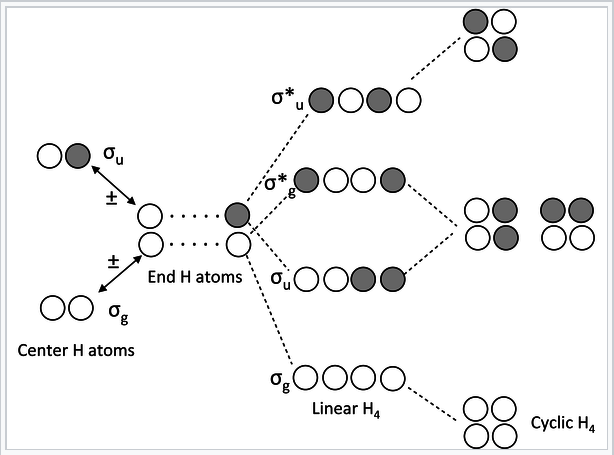
Cadenas y anillos de cuatro átomos de H o π-orbitales (H ₄ o butadieno):

Diagrama MO para H4 o butadieno

Algunas notas sobre este diagrama MO:

• En la forma lineal de la molécula, la combinación de AO hace una escalera de niveles de energía uniformemente espaciados que alternan g — u — g — u... Cada orbital sucesivo tiene un nodo más. Esta es una regla general para cadenas lineales de orbitales σ o π con números pares de átomos.

• En la forma cíclica de la molécula, hay un orbital no degenerado en la parte inferior, uno en la parte superior, y una escalera de orbitales doblemente degenerados en el medio. Esta es también una regla general para moléculas cíclicas con números pares de átomos. Este es el origen de la regla 4n+2 para los aromáticos.

• H ₄ tiene cuatro electrones de valencia, y por analogía el butadieno tiene cuatro electrones π. Estos electrones llenan los dos MO más bajos en la forma lineal de la molécula, correspondientes a dos enlaces p conjugados en butadieno (H ₂ C=CH-CH=CH ₂).

• En la forma cíclica de la molécula, los orbitales degenerados están ocupados individualmente. La molécula puede romper la degeneración (y disminuir su energía) distorsionándose a un rectángulo arrugado. Esta es una regla general para las moléculas cíclicas antiaromáticas (regla 4n). Así, el ciclobutadieno debe ser antiaromático y tener dos enlaces simples y dos dobles que no se deslocalizan por resonancia.

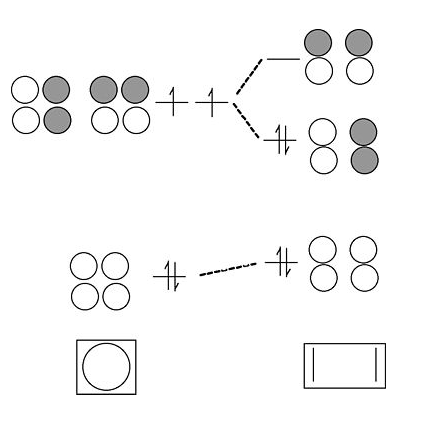
El ciclobutadieno es en realidad una molécula muy inestable porque polimeriza para aliviar la tensión del anillo. Los derivados de la molécula con impedimento esterico tienen la estructura rectangular plegada predicha por la teoría MO.

Orbitales π-benceno:

¿Cómo se obtiene de una cadena de 4 átomos a 6 átomos?

Por analogía al proceso que solíamos pasar de una cadena de 2 átomos a una cadena de 4 átomos, ahora pasamos de 4 a 6. Comenzamos con los orbitales de la cadena de 4 átomos, que forman una escalera de orbitales g y u. Después hacemos combinaciones g y u de los dos átomos que estamos agregando en los extremos. Al combinar g's con g's y u's con u's, terminamos con las soluciones para una cadena de 6 átomos. El cierre de estos orbitales en un bucle nos da los orbitales moleculares π de la molécula de benceno. El resultado son tres bonos π, como esperábamos. El benceno se ajusta a la regla 4n+2 (n=2) y por lo tanto es aromático.

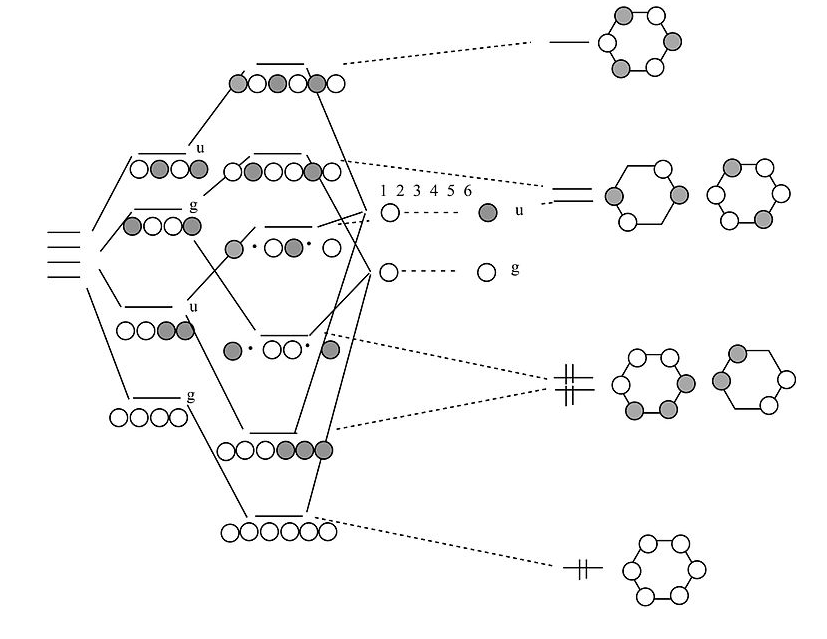
Aquí hemos utilizado la analogía isolobular para construir diagramas MO para sistemas de enlace π, como etileno y benceno, a partir de combinaciones de orbitales s. Se plantea la interesante pregunta de si la regla aromática 4n+2 podría aplicarse a los sistemas s-orbitales, es decir, si tres moléculas de H ₂ podrían juntarse para formar una molécula aromática H ₆. De hecho, estudios recientes de hidrógeno bajo presiones ultra altas en una celda de yunque de diamante muestran que tales estructuras sí se forman. Existe una fase sólida de hidrógeno que contiene láminas de anillos distorsionados de seis miembros, análogas a la red 2D completamente conectada de anillos de seis miembros que se encuentran en grafito o grafeno. ^[6]

Ahora debería ser evidente a partir de nuestra construcción de diagramas MO para moléculas de cuatro y seis orbitales que podemos seguir agregando orbitales atómicos para hacer cadenas y anillos de 8, 10, 12... átomos. En cada caso, los orbitales g y u forman una escalera de MO. En el peldaño inferior de la escalera de una cadena N-atómica, no hay nodos en el MO, y agregamos un nodo por cada peldaño hasta llegar a la cima, donde hay N-1 nodos. Otra forma de decir esto es que la longitud de onda de un electrón en orbital x, contando desde el fondo (1,2,3... x,... N), es 2nA/x, donde a es la distancia entre átomos. Encontraremos en los Capítulos 6 y 10 que podemos aprender mucho sobre las propiedades electrónicas de los metales y semiconductores a partir de este modelo, utilizando la cadena infinita de átomos como modelo para el cristal.