5.2: Recuento de electrones en complejos de metales de transición

Última actualización
Guardar como PDF

Page ID: 72345

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Los orbitales d son los orbitales fronterizos (HOMO y LUMO) de los complejos de metales de transición. Muchas de las propiedades importantes de los complejos -su forma, color, magnetismo y reactividad- dependen de la ocupación electrónica de los orbitales d del metal. Para entender y racionalizar estas propiedades es importante saber contar los electrones d.

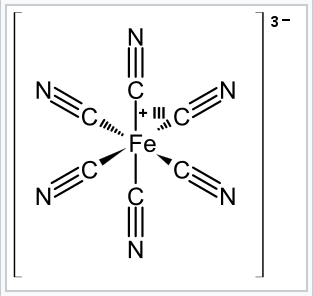
Debido a que los metales de transición son generalmente menos electronegativos que los átomos en los ligandos (C, N, O, Cl, P...) que forman el enlace metal-ligando, nuestra convención es asignar ambos electrones en el enlace al ligando. Por ejemplo, en el complejo ferricianuro [Fe (CN) ₆] ^3-, si el ligando de cianuro mantiene ambos electrones se formula como CN ^-. Por diferencia, el hierro debe ser Fe ³⁺ porque las cargas (3 ⁺ + 6 (1 ^-)) deben sumar a la carga general -3 en el complejo.

El siguiente paso es determinar cuántos electrones d tiene el ion Fe ³⁺. La regla es contar todos los electrones de valencia del hierro como electrones d. El hierro está en el grupo 8, entonces

grupo 8 - 3+ carga = d ⁵ (o 3d ⁵)

8 - 3 = 5

Estructura del anión ferricianuro octaédrico. Debido a que la carga general del complejo es 3-, el Fe se encuentra en el estado de oxidación +3 y su recuento de electrones es 3d ⁵.

El mismo procedimiento se puede aplicar a cualquier complejo de metal de transición. Por ejemplo, considere el complejo [Cu (NH ₃) ₄] ²⁺. Debido a que el amoníaco es un ligando neutro, el Cu se encuentra en el estado de oxidación 2+. El cobre (II), en el grupo 11 de la tabla periódica tiene 11 electrones en su caparazón de valencia, menos dos, dejándolo con 9 electrones d (3d ⁹). En el complejo neutro [Rh (OH) ₃ (H ₂ O) ₃], Rh está en el estado de oxidación +3 y está en el grupo 9, por lo que el recuento de electrones es 4d ⁶. El zinc (II) en el grupo 12 tendría 10 electrones d en [Zn (NH ₃) ₄] ²⁺, una capa completa, y el manganeso (VII) tiene cero electrones d en MnO ₄ ^-. Níquel carbonilo, Ni (CO) ₄, contiene el ligando neutro de CO y Ni en el estado de oxidación cero. Dado que Ni está en el grupo 10, contamos los electrones en Ni como 3d ¹⁰.

Una fuente frecuente de confusión sobre el conteo de electrones es el destino de los electrones s en el metal. Por ejemplo, nuestras reglas de conteo de electrones predicen que Ti es 3d ¹ en el complejo octaédrico [Ti (H ₂ O) ₆] ³⁺. Pero la configuración electrónica de un átomo de Ti libre, según el principio Aufbau, es 4s ² 3d ². ¿Por qué es el Ti ³⁺ ion 3d ¹ y no 4s ¹? De igual manera, ¿por qué asignamos Mn ²⁺ como 3d ⁵ en lugar de 4s ² 3d ³? La respuesta corta es que los orbitales metálicos son más altos en energía en un complejo metálico que en el átomo libre porque tienen carácter antienlace. Justificaremos esta afirmación con un diagrama MO en la Sección 5.2.

Método de Clasificación de Enlace Covalente (CBC). Si bien la regla de conteo de electrones que hemos desarrollado anteriormente es útil y funciona de manera confiable para todo tipo de complejos, la asignación de todos los electrones compartidos en el complejo a los ligandos no siempre representa la verdadera imagen de unión. Esta imagen sería más precisa en el caso de ligandos que son mucho más electronegativos que el metal. Pero de hecho, hay todo tipo de ligandos, incluyendo aquellos como H, alquilo, ciclopentadienuro, y otros donde el metal y ligando tienen electronegatividad comparable. En esos casos, especialmente con metales de transición tardíos que son relativamente electropositivos, debemos considerar el enlace metal-ligando como covalente. El método CBC, también denominado notación LXZ, fue introducido en 1995 por M. L. H. Green ^[2] para describir mejor los diferentes tipos de enlaces metal-ligando. Las imágenes orbitales moleculares a continuación resumen la diferencia entre los ligandos L, X y Z. ^[3] De estos, L y X son los tipos más comunes.

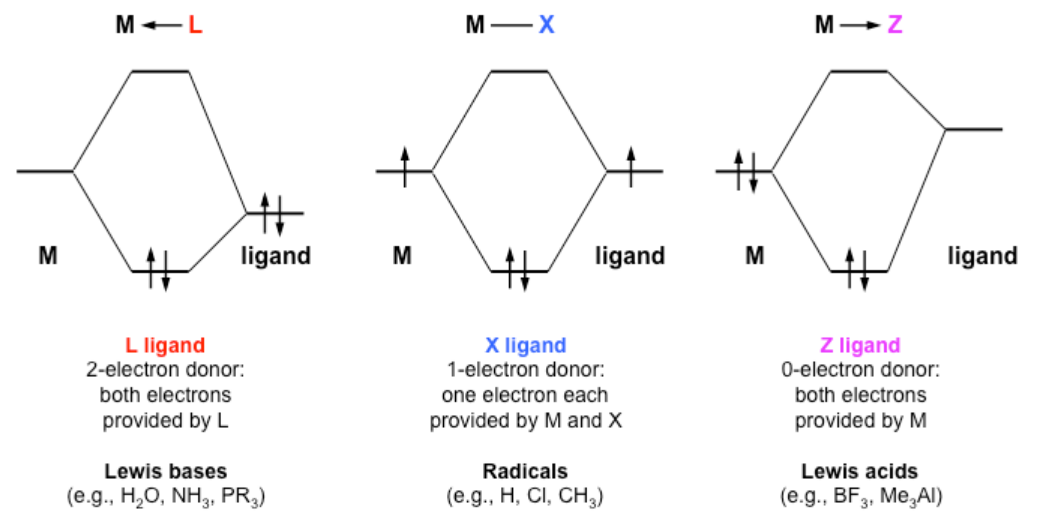
Los ligandos tipo L son bases de Lewis que donan dos electrones al centro metálico independientemente del método de conteo de electrones que se utilice. Estos electrones pueden provenir de pares solitarios, donantes pi o sigma. Los enlaces formados entre estos ligandos y el metal son enlaces covalentes dativos, que también se conocen como enlaces coordinados. Ejemplos de este tipo de ligando incluyen CO, PR ₃, NH ₃, H ₂ O, carbenos (=CRR') y alquenos.

Los ligandos tipo X son aquellos que donan un electrón al metal y aceptan un electrón del metal cuando se usa el método de conteo de electrones con ligandos neutros, o donan dos electrones al metal cuando se usa el método de conteo de electrones por pares donantes. ^[4] Independientemente de que se considere neutro o aniónico, estos ligandos producen enlaces covalentes normales. Algunos ejemplos de este tipo de ligando son H, CH ₃, halógenos y NO (doblado).

Los ligandos de tipo Z son aquellos que aceptan dos electrones del centro metálico en oposición a la donación que ocurre con los otros dos tipos de ligandos. Sin embargo, estos ligandos también forman enlaces covalentes dativos como el tipo L. Este tipo de ligando no se suele utilizar, ya que en ciertas situaciones puede escribirse en términos de L y X. Por ejemplo, si un ligando Z va acompañado de un tipo L, se puede escribir como X ₂. Ejemplos de estos ligandos son ácidos de Lewis, tales como BR ₃.

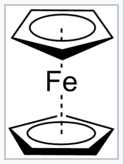
Ferroceno

Algunos ligandos multidentados pueden actuar como una combinación de tipos de ligandos. Un ejemplo famoso es el ligando ciclopentadienilo (o Cp), C ₅ H ₅. Clasificaríamos este ligando neutro como [L ₂ X], con las dos funcionalidades L correspondientes a los dos fragmentos “olefínicos” mientras que la funcionalidad X corresponde al carbono “radical” CH en el anillo. La adición de un electrón hace que el anión Cp ^-, que tiene seis electrones pi y es así plano y aromático. ^{En el complejo de ferroceno, Cp ₂ Fe, utilizando el método de conteo de pares donantes “estándar” podemos considerar a los dos ligandos Cp como cada uno poseyendo seis electrones pi, y por diferencia Fe está en el estado de oxidación +2.} El ion Fe ²⁺ es d ⁶. Así, el átomo de hierro en el complejo (independientemente del método de conteo) tiene 6+6+6=18 electrones en su entorno de coordinación, que es un recuento de electrones particularmente estable para los complejos de metales de transición.