5.3: Teoría del Campo Cristalino

La teoría del campo cristalino es uno de los modelos más simples para explicar las estructuras y propiedades de los complejos de metales de transición. La teoría se basa en la electrostática de la interacción metal-ligando, por lo que sus resultados son solo aproximados en los casos en que el enlace metal-ligando es sustancialmente covalente. Pero debido a que el modelo hace un uso efectivo de la simetría molecular, puede ser sorprendentemente preciso al describir el magnetismo, los colores, la estructura y la estabilidad relativa de los complejos metálicos.

Considerar un ion metálico cargado positivamente como Fe ³⁺ en el “campo” de seis ligandos cargados negativamente, como CN ^-. Hay dos términos energéticos que debemos considerar. La primera es la atracción electrostática entre el metal y los ligandos, que es inversamente proporcional a la distancia entre ellos:

\[E_{elec} = \frac{1}{4\pi\varepsilon_{0}} \sum_{ligands} \frac{q_{M}q_{L}}{r_{ML}}\]

El segundo término es la repulsión que surge del principio de exclusión Pauli cuando se agrega un tercer electrón a un orbital lleno. No hay lugar para que este tercer electrón vaya excepto a un orbital antienlace de mayor energía. Esta es la situación cuando un par solitario de ligandos se acerca a un metal ocupado d-orbital:

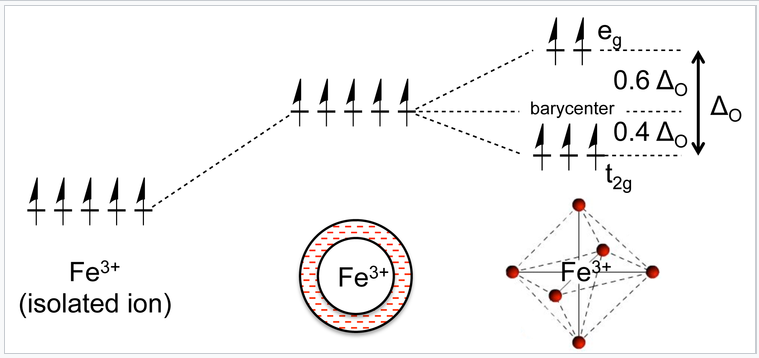
Ahora consideremos el efecto de estos términos atractivos y repulsivos a medida que se juntan el ion metálico y los ligandos. Esto lo hacemos en dos pasos, primero formando una “esfera” ligando alrededor del metal y luego moviendo los seis ligandos a los vértices de un octaedro. Inicialmente los cinco orbitales d son degenerados, es decir, tienen la misma energía por simetría. En el primer paso, la interacción antiadhesión impulsa la energía de los orbitales, pero permanecen degenerados. En el segundo paso, los orbitales d se dividieron en dos clases de simetría, un conjunto triplemente degenerado de menor energía (los orbitales t _2g) y un conjunto doblemente degenerado de mayor energía (los orbitales e _g).

Un ion Fe ^3+ tiene cinco electrones d, uno en cada uno de los cinco orbitales d. En un campo de ligando esférico, la energía de los electrones en estos orbitales aumenta debido a la interacción repulsiva con los pares solitarios del ligando. Los orbitales se dividen en dos niveles de energía cuando los ligandos ocupan los vértices de un octaedro, pero la energía promedio sigue siendo la misma.

A la diferencia de energía entre los orbitales e _g y t _2g se le da el símbolo Δ _O, donde la “O” significa “octaédrico”. Veremos que esta energía de división es sensible al grado de superposición orbital y por lo tanto depende tanto del metal como del ligando. En relación con la energía del punto medio (el baricentro), los orbitales t _2g se estabilizan por 2/5 Δ _O y los orbitales e _g se desestabilizan por 3/5 Δ _O en un complejo octaédrico.

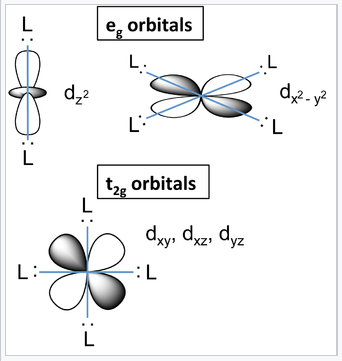
d-orbitales y su orientación con relación a ligandos en un complejo octaédrico.

¿Qué causa que los orbitales d se dividan en dos conjuntos? Recordemos que los orbitales d tienen una orientación específica con respecto a los ejes cartesianos. Los lóbulos de los orbitales d _xy, d _xz y d _yz (los orbitales t _2g) se encuentran en los planos xy-, xz- e yz, respectivamente. Estos tres orbitales d tienen nodos a lo largo de las direcciones x, y y z. Los orbitales que contienen los pares solitarios del ligando están orientados a lo largo de estos ejes y por lo tanto tienen un solapamiento cero con los orbitales metálicos t _2g. Es fácil ver que estos tres orbitales d deben ser degenerados por la simetría. Por otro lado, los lóbulos de los orbitales d _{z ²} y d _{x ² -y ²} (los orbitales e _g) apuntan directamente a lo largo de los ejes de unión y tienen un fuerte solapamiento con los orbitales del ligando. Si bien es menos intuitivamente obvio, estos orbitales también son degenerados por la simetría y tienen carácter antiadherentes.

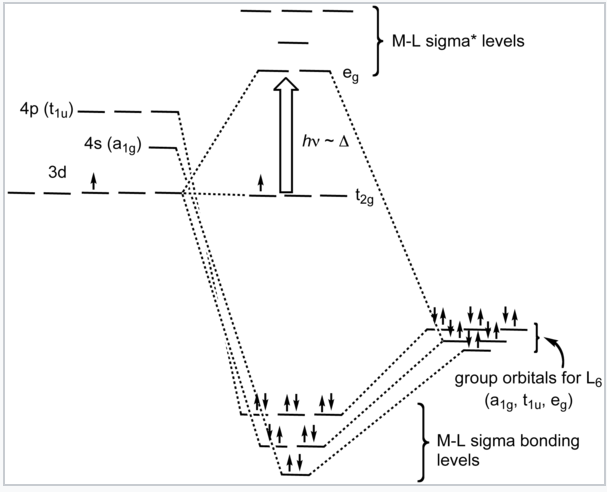
Es informativo comparar los resultados de la teoría de campos cristalinos y la teoría orbital molecular (también llamada teoría de campo de ligandos en este contexto) para un complejo octaédrico de metal de transición. Los diagramas de nivel de energía a continuación hacen esta comparación para el ion octaédrico d ¹ [Ti (H ₂ O) ₆] ³⁺. En la siguiente imagen MO, los orbitales fronterizos se derivan de los orbitales d metálicos. El conjunto inferior de t _2g, que contiene un electrón, no se une por simetría, y los orbitales e _g son antiadherentes. El metal 4s orbital, que tiene una simetría _1g, hace una combinación de unión de baja energía que está centrada en ligando, y una combinación antiunión que está centrada en metal y por encima de los niveles de e _g. Esta es la razón por la que nuestras reglas de conteo de electrones d no necesitan considerar el metal 4s orbital. El mensaje importante para llevar a casa es que la teoría de campos cristalinos y la teoría MO dan resultados muy similares para los orbitales fronterizos de los complejos de metales de transición.

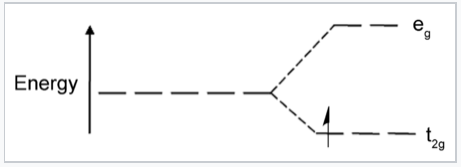
Diagrama de energía de campo cristalino para el complejo octaédrico d ^1 [Ti (H 2 O) 6] ^3+.

Diagrama ligando-campo para el complejo octaédrico [Ti (H 2 O) 6] ^3+.