5.8: Efecto Jahn-Teller
- Page ID
- 72294
El efecto Jahn-Teller, a veces también conocido como distorsión Jahn-Teller, describe la distorsión geométrica de moléculas e iones que está asociada con ciertas configuraciones de electrones. Este efecto electrónico lleva el nombre de Hermann Arthur Jahn y Edward Teller, quienes demostraron, usando la teoría de grupos, que las moléculas orbitalmente degeneradas no pueden ser estables. [15] El teorema de Jahn-Teller establece esencialmente que cualquier molécula no lineal con un estado básico electrónico espacialmente degenerado sufrirá una distorsión geométrica que elimina esa degeneración, porque la distorsión disminuye la energía general de la molécula.
|
Distorsión Jahn-Teller de un complejo octaédrico d 9 de metal de transición. La distorsión tetragonal alarga los enlaces a lo largo del eje z a medida que los enlaces en el plano x-y se vuelven más cortos. Este cambio disminuye la energía general, debido a que los dos electrones en el orbital d z2 bajan de energía a medida que sube el electrón en el orbital d x2-y2. |
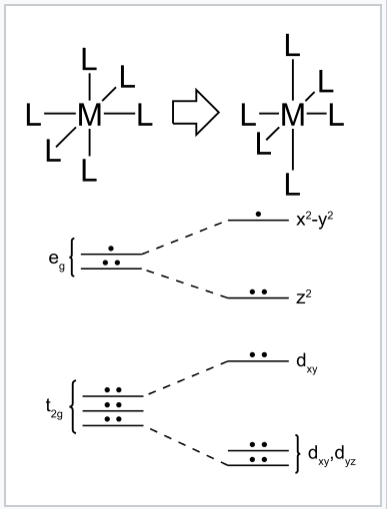
Podemos entender este efecto en el contexto de los complejos metálicos octaédricos considerando configuraciones de electrones d en las que el conjunto orbital e g contiene uno o tres electrones. Los más comunes de estos son alto giro d 4 (por ejemplo, CrF 2), giro bajo d 7 (por ejemplo, NaNIO 2) y d 9 (por ejemplo, Cu 2+). Si el complejo puede distorsionarse para romper la simetría, entonces uno de los orbitales (antes) degenerados e g bajará en energía y el otro subirá. Más electrones ocuparán el orbital inferior que el superior, resultando en una disminución general de la energía electrónica. Una distorsión similar puede ocurrir en complejos tetraédricos cuando los orbitales t 2 están parcialmente llenos. Se dice que tales distorsiones geométricas que bajan la energía electrónica son impulsadas electrónicamente. Distorsiones similares impulsadas electrónicamente ocurren en compuestos de cadena unidimensionales, donde se llaman distorsiones de Peierls, y en láminas unidas bidimensionalmente, donde se llaman ondas de densidad de carga.
El efecto Jahn-Teller se encuentra con mayor frecuencia en los complejos octaédricos, especialmente en los complejos de cobre (II) de seis coordenadas. [16] La configuración electrónica d 9 de este ion da tres electrones en los dos orbitales e g degenerados, lo que lleva a un estado básico electrónico doblemente degenerado. Dichos complejos se distorsionan a lo largo de uno de los cuatro ejes moleculares (siempre etiquetados como eje z), lo que tiene el efecto de eliminar las degeneraciones orbitales y electrónicas y disminuir la energía general. La distorsión normalmente toma la forma de alargar los enlaces a los ligandos que se encuentran a lo largo del eje z, pero ocasionalmente ocurre como un acortamiento de estos enlaces (el teorema de Jahn-Teller no predice la dirección de la distorsión, solo la presencia de una geometría inestable). Cuando se produce tal elongación, el efecto es disminuir la repulsión electrostática entre el par de electrones en el ligando básico de Lewis y cualquier electrón en orbitales con un componente z, disminuyendo así la energía del complejo. Si se esperara que el complejo no distorsionado tuviera un centro de inversión, éste se conserva después de la distorsión.
|
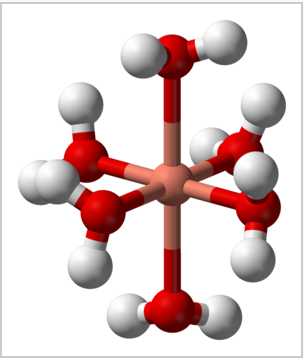
El efecto Jahn-Teller es responsable de la distorsión tetragonal del ion complejo hexaacuacopper (II), [Cu (OH 2) 6] 2+, que de otro modo podría poseer geometría octaédrica. Las dos distancias axiales Cu−O son 2.38 Å, mientras que las cuatro distancias ecuatoriales Cu−O son ~1.95 Å. |
En los complejos octaédricos, el efecto Jahn-Teller es más pronunciado cuando un número impar de electrones ocupa los orbitales e g. Esta situación surge en complejos con las configuraciones d 9, complejos d 7 de bajo giro o d 4 de alto giro, todos los cuales tienen estados básicos doblemente degenerados. En tales compuestos los orbitales e g involucrados en la degeneración apuntan directamente a los ligandos, por lo que la distorsión puede resultar en una gran estabilización energética. Estrictamente hablando, el efecto también ocurre cuando hay una degeneración debido a los electrones en los orbitales t 2g (es decir, configuraciones como d 1 o d 2, ambas de las cuales son triplicamente degeneradas). En tales casos, sin embargo, el efecto es mucho menos notable, debido a que hay una disminución mucho menor de la repulsión al tomar ligandos más lejos de los orbitales t 2g, que no apuntan directamente a los ligandos (ver la tabla a continuación). Lo mismo ocurre en los complejos tetraédricos (por ejemplo, manganato: la distorsión es muy sutil porque hay menos estabilización que ganar porque los ligandos no están apuntando directamente a los orbitales.
Los efectos esperados para la coordinación octaédrica se dan en la siguiente tabla:
| Número de electrones d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Spin alto/bajo | HS | LS | HS | LS | HS | LS | HS | LS | ||||||
| Fuerza del efecto J-T | w | w | s | w | w | w | w | s | s | |||||
w: débil efecto Jahn-Teller (t 2g orbitales ocupados de manera desigual)
s: fuerte efecto Jahn-Teller esperado (e g orbitales ocupados de manera desigual)
en blanco: no se espera ningún efecto Jahn—Teller.
El efecto Jahn-Teller se manifiesta en los espectros de absorbancia UV-VIS de algunos compuestos, donde a menudo causa división de bandas. Es fácilmente evidente en las estructuras de muchos complejos de cobre (II). [17] Se puede obtener información adicional detallada sobre la anisotropía de dichos complejos y la naturaleza de la unión del ligando a partir de la estructura fina de los espectros de resonancia de espín electrónico a baja temperatura.
|
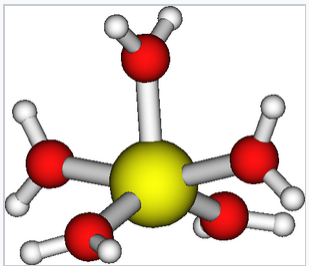
El ion Cu (II) también puede coordinar cinco moléculas de agua en una pirámide cuadrada alargada con cuatro enlaces Cu-Oeq (2x1.98 Å y 2x1.95 Å) y un enlace Cu-Oax largo (2.35 Å). Los cuatro ligandos ecuatoriales están distorsionados a partir del plano ecuatorial medio ± 17°. |