5.9: Complejos Tetraédricos

Última actualización
Guardar como PDF

Page ID: 72357

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Los complejos tetraédricos se forman con iones de metales de transición tardíos (Co ^²⁺, Cu ²⁺, Zn ^{2+, Cd 2+}) y algunos metales de transición tempranos (Ti ⁴⁺, Mn ²⁺), especialmente en situaciones donde los ligandos son grandes. En estos casos, el ion metálico pequeño no puede acomodar fácilmente un número de coordinación superior a cuatro. Ejemplos de iones y moléculas tetraédales son [COCl ₄] ^2-, [MnCl ₄] ^2-, y TiX ₄ (X = halógeno). También se observa coordinación tetraédrica en algunos oxo-aniones como [FeO _{4] 4} ^-, que existe como aniones discretos en las sales Na ₄ FeO ₄ y Sr ₂ FeO ₄, y en los óxidos neutros RuO ₄ y OSo ₄. Los complejos carbonílicos metálicos Ni (CO) ₄ y Co (CO) ₄] ^- también son tetraédricos.

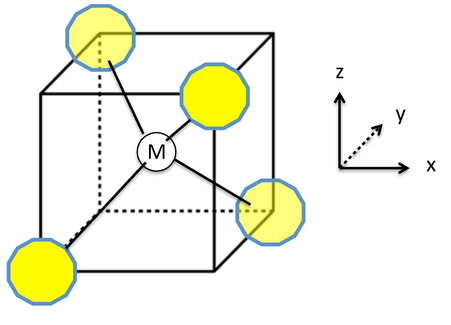
Una molécula de tetraedro con sus vértices conectados a un cubo. Una pequeña gráfica a la derecha del cubo indica el ángulo recto.

La división de los orbitales d en un campo cristalino tetraédrico se puede entender conectando los vértices de un tetraedro para formar un cubo, como se muestra en la imagen de la izquierda. Los enlaces tetraédricos M-L se encuentran a lo largo de las diagonales del cuerpo del cubo. Los orbitales d _z 2 y d _x 2 _-y 2 apuntan a lo largo de los ejes cartesianos, es decir, hacia las caras del cubo, y tienen el menor contacto con los pares solitarios del ligando. Por lo tanto estos dos orbitales forman un conjunto e de baja energía, doblemente degenerado. Los orbitales d _xy, d _yz y d _xz apuntan a los bordes del cubo y forman un conjunto t ₂ triplicamente degenerado. Mientras que los orbitales t ₂ tienen más solapamiento con los orbitales ligando que el conjunto e, siguen interactuando débilmente en comparación con los orbitales e _g de un complejo octaédrico.

El diagrama de energía del campo cristalino resultante se muestra a la derecha. La energía de división, Δ _t, es aproximadamente 4/9 la división de un complejo octaédrico formado con los mismos ligandos. Para los elementos 3d, Δ _t es así pequeño en comparación con la energía de emparejamiento y sus complejos tetraédricos son siempre de alto espín. Tenga en cuenta que hemos bajado el subíndice “g” porque el tetraedro no tiene un centro de simetría.

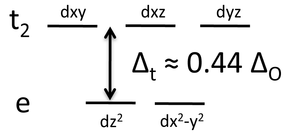
Un diagrama de energía con dos niveles. T 2 en la parte superior con 3 orbitales: d x y, d x z, y d y z. E en la parte inferior con dos niveles de energía: d z cuadrado y d x cuadrado - y cuadrado. La energía de división entre ellos, delta t, es aproximadamente 0.44.

Los complejos tetraédricos suelen tener colores vibrantes porque carecen del centro de simetría que prohíbe una transición d-d*. Debido a que se permite la transición de baja energía, estos complejos normalmente absorben en el rango visible y tienen coeficientes de extinción que son 1-2 órdenes de magnitud mayores que los de los complejos octaédricos correspondientes. Una ilustración de este efecto se puede ver en Drierite, que contiene partículas de sulfato de calcio anhidro incoloro (yeso) que absorbe la humedad de los gases. El colorante indicador en Drierite es cloruro de cobalto (II), que es un rosa claro cuando está húmedo (octaédrico) y azul profundo cuando está seco (tetraédrico). La reacción de hidratación reversible es:

\[\ce{Co[CoCl4] + 12H2O -> 2 Co(H2O)6Cl2}\]

(azul profundo, CoCl tetraédrico ₄ ^2-) (rosa claro, octaédrico [Co (H ₂ O) ₆] ²⁺)

Dos platillos con complejos de cobalto y sus correspondientes diagramas de energía. La izquierda es tetraédrica y tiene rocas azules y blancas. Siete electrones en un diagrama de alta energía de espín con tres orbitales t 2 y dos orbitales e. La derecha es octaédrica y tiene rocas blancas y moradas. Diagrama de alta energía de giro con dos orbitales t 2 y tres orbitales e.