6.2: Celdas unitarias y estructuras cristalinas

Última actualización
Guardar como PDF

Page ID: 71954

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

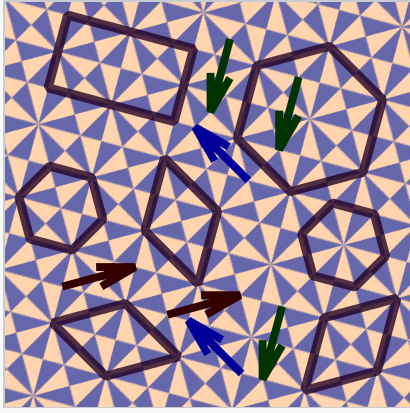
Se puede pensar en los cristales como patrones repetitivos, al igual que el papel tapiz o los azulejos del baño, pero en tres dimensiones. La unidad repetitiva fundamental del cristal se llama celda unitaria. Es una forma tridimensional que se puede repetir una y otra vez mediante traslaciones unitarias para llenar el espacio (y dejar espacios mínimos) en la estructura. Algunas posibles celdas unitarias se muestran en el patrón de mosaico a la derecha, junto con flechas que indican vectores de traducción unitaria. En tres dimensiones, las celdas unitarias hexagonales o rómbicas de este patrón serían reemplazadas por cajas tridimensionales que se apilarían juntas para llenar todo el espacio. Como se muestra en la figura, el origen de la celda unitaria es arbitrario. El mismo conjunto de cajas llenará todo el espacio sin importar dónde definamos el origen de la celosía. Veremos que los metales puros suelen tener estructuras cristalinas muy simples con celdas unitarias cúbicas o hexagonales. Sin embargo, las estructuras cristalinas de las aleaciones pueden ser bastante complicadas.

Al considerar las estructuras cristalinas de metales y aleaciones, no es suficiente pensar en cada átomo y sus ligandos vecinos como un sistema aislado. En cambio, piense en todo el cristal metálico como una red de átomos conectados por un mar de electrones de valencia compartidos. Los electrones están deslocalizados porque no hay suficientes de ellos para llenar cada “enlace” entre átomos con un par de electrones. Por ejemplo, en las estructuras cristalinas de los metales del bloque s y del bloque p, cada átomo tiene 8 o 12 vecinos más cercanos, pero el número máximo de electrones s + p es 8. Así, no hay suficientes para poner dos electrones entre cada par de átomos. Los metales de transición también pueden usar sus orbitales d en la unión, pero de nuevo nunca hay suficientes electrones para llenar completamente todos los “enlaces”.

Tres hexágonos, tres diamantes y un rectángulo encima de un patrón de triángulo púrpura y naranja. Dos flechas rojas en la misma dirección, tres flechas verdes en la misma dirección y dos flechas azules en la misma dirección indican puntos de celosía.

Posibles celdas unitarias en un patrón de teselas periódico. Las flechas conectan puntos traslacionalmente equivalentes (puntos de celosía) en el patrón.

Los átomos en una red metálica se disponen en un cierto patrón que se puede representar como una estructura de caja 3D conocida como la celda unitaria que se repite en todo el metal.

Cúbico Simple	Centrada Cuerpo Cúbico	Centrada Cara Cúbica	Cierre Hexagonal Embalado

1 átomo/celda	2 átomos/celda	4 átomos/celda	2 átomos/celda

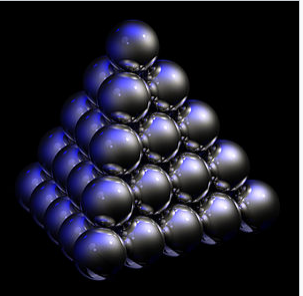
Los átomos metálicos se pueden aproximar como esferas, y por lo tanto no son 100% eficientes en el empaque, de la misma manera que una pila de balas de cañón tiene algunos espacios vacíos entre las bolas. Diferentes celdas unitarias tienen diferentes eficiencias de empaque. El número de átomos que se incluye en la celda unitaria solo incluye las fracciones de átomos dentro de la caja. Los átomos en las esquinas de la celda unitaria cuentan como 1/8 de un átomo, los átomos en una cara cuentan como ½, un átomo en el centro cuenta como un átomo completo. Usando esto, calculemos el número de átomos en una celda unitaria cúbica simple, una celda unitaria cúbica centrada en la cara (fcc) y una celda unitaria cúbica centrada en el cuerpo (bcc).

Cúbico Simple:

8 átomos de esquina × 1/8 = 1 átomo/celda. El empaque en esta estructura no es eficiente (52%) y por lo tanto este tipo de estructura es muy raro para metales.

Centrada en el cuerpo cúbico, bcc:

(8 átomos de esquina × 1/8) + (1 átomo central × 1) = 2 átomos/celda. El empaque es más eficiente (68%) y la estructura es común para metales alcalinos y metales de transición temprana. Aleaciones como el latón (CuZn) también adoptan estas estructuras.

Centrada en la cara cúbica, fcc (también llamado Cubic Close Packed, ccp):

(8 átomos de esquina × 1/8) + (6 átomos faciales × ½) = 4 átomos/celda. Esta estructura, junto con su relativo hexagonal (hcp), tiene el empaque más eficiente (74%). Muchos metales adoptan la estructura fcc o hcp.

Empaquetado con cierre hexagonal, hcp:

Al igual que la estructura fcc, la densidad de empaque de hcp es de 74%.

La celda unitaria de un metal bcc contiene dos átomos.

Cálculo de la fracción de empaque. Las fracciones de empaquetamiento de las estructuras cristalinas mostradas anteriormente se pueden calcular dividiendo el volumen de los átomos en la celda por el volumen de la propia celda. El volumen de los átomos en la celda es igual al número de átomos/celda multiplicado por el volumen de una esfera, (4/3) πr ³. El volumen de las celdas cúbicas se encuentra al cubicar la longitud lateral. Como ejemplo, calculemos la eficiencia de empaque de una celda unitaria cúbica simple. Como vimos anteriormente en la sección, una celda unitaria cúbica simple contiene un átomo. La longitud lateral de la celda unitaria cúbica simple es 2r, ya que los centros de cada átomo ocupan las esquinas de la celda unitaria.

\[\textrm{Packing efficiency} = \frac{(1 \: atom) \times (\frac{4}{3}) \pi r^{3}}{(2r)^{3}}= 0.523\]

El mismo método se puede aplicar a estructuras bcc y fcc.

Balas de cañón apiladas en una pirámide. La base es un cuadrado de cinco por cinco, luego una capa de cuatro por cuatro, una capa de tres por tres, una capa de dos por dos, y una bala de cañón en la parte superior.

Pila cúbica de balas de cañón centradas en la cara.