6.5: Adhesión en Metales

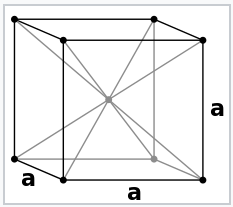
La descripción de pares de electrones de los enlaces químicos, que fue la base de la regla del octeto para los compuestos del bloque p, se descompone para los metales. Esto se ilustra bien con el metal Na, cuya estructura se muestra a la izquierda. Na tiene muy pocos electrones de valencia para hacer enlaces de pares de electrones entre cada par de átomos. Podríamos pensar en la celda unitaria de Na como que tiene ocho estructuras de resonancia sin enlace en las que solo un enlace Na-Na por celda contiene un par de electrones.

El metal de sodio cristaliza en la estructura cúbica centrada en el cuerpo, en la que cada átomo tiene ocho vecinos más cercanos. Dado que la configuración electrónica de Na es [Ar] 3s ^1, solo hay dos electrones de valencia por celda unitaria que se comparten entre ocho enlaces Na-Na. Esto significa que el orden de unión Na-Na es 1/8 en metal Na.

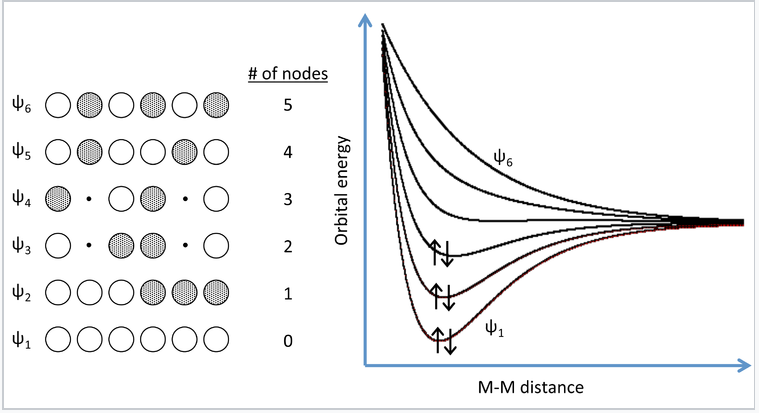
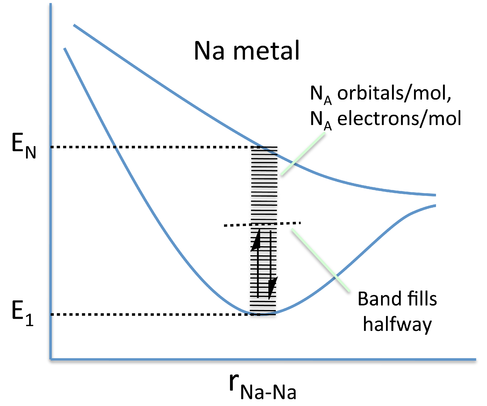
Una manera más realista de describir la unión en metales es a través de la teoría de bandas. La evolución de las bandas de energía en sólidos a partir de la teoría simple de MO (Capítulo 2) se ilustra a la derecha para una cadena de seis átomos de Na, cada uno de los cuales tiene un orbital de valencia 3s y aporta un electrón de valencia. En general, n orbitales atómicos (en este caso los seis orbitales Na 3s) generarán n orbitales moleculares con n-1 posibles nodos. En el Capítulo 2, mostramos que el gráfico de energía versus distancia internuclear para un sistema de dos átomos de hidrógeno tiene un bajo nivel de energía y un alto nivel de energía correspondientes a los orbitales moleculares de enlace y antienlace, respectivamente. Estos dos niveles de energía estaban bien separados entre sí, y los dos electrones en H ₂ prefieren energéticamente el nivel de energía más bajo. Si se introducen más átomos en el sistema, habrá una serie de niveles adicionales entre los niveles de energía más bajos y más altos.

Imagen MO para una cadena lineal de seis átomos de Na. Tres de los seis MO pueden acomodar los seis electrones de valencia. Agregar más átomos a la cadena hace más orbitales moleculares de energía intermedia, que eventualmente se funden en una banda continua de orbitales. Para Na, la banda 3s siempre está medio llena porque cada MO puede acomodar dos electrones.

En teoría de bandas, la cadena atómica se extrapola a un número muy grande -del orden de 10 ²² átomos en un cristal- de manera que las diferentes combinaciones de orbitales enlazantes y antiligantes crean “bandas” de posibles estados energéticos para el metal. En el lenguaje de la física, este enfoque de construir las bandas a partir de orbitales atómicos discretos se denomina aproximación “vinculante”. El número de átomos es tan grande que las energías pueden pensarse como un continuo en lugar de una serie de niveles distintos. Un metal sólo llenará parcialmente esta banda, ya que hay menos electrones de valencia de los que hay estados energéticos para llenar. En el caso del Na metal, esto da como resultado una banda de 3s medio llena.

Modelo de electrones casi libres

En los metales, los electrones de valencia se deslocalizan sobre muchos átomos. La energía total de cada electrón viene dada por la suma de su energía cinética y potencial:

E = KE + PE

E ≈ p ² /2m + V

donde p es el momento del electrón (una cantidad vectorial), m es su masa, y V es un potencial promedio que el electrón siente de los núcleos positivos de los átomos. Este potencial mantiene los electrones de valencia en el cristal pero, en el modelo de electrones libres, es esencialmente uniforme a través del cristal.

Longitud de onda y número de onda de electrones

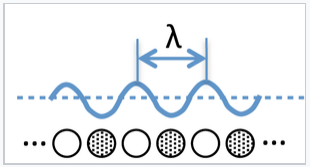
¿Cuáles son las consecuencias de este modelo para la teoría de bandas? Para una hipotética cadena infinita (es decir, un cristal 1D) de átomos de Na, los orbitales moleculares en la parte inferior de la banda 3s se unen completamente y la longitud de onda de los electrones (2x la distancia entre nodos) en estos orbitales es muy larga. En la parte superior de la banda, el orbital más alto es completamente antienlace y la longitud de onda es 2 veces la distancia entre átomos (2a), ya que hay un nodo por átomo. Recuerde que la longitud de onda de un electrón (λ) es inversamente proporcional a su impulso p, según la relación de Broglie λ = h/p.

Para un electrón (casi) libre, la energía cinética se puede expresar en términos de su longitud de onda, usando KE = p ^2/2m y la relación de Broglie:

\[KE=\frac{p^{2}}{2m} = \frac{h^{2}}{2m\lambda ^ {2}}\]

Podemos pensar en la longitud de onda de un electrón en un orbital molecular como el doble de la distancia entre nodos. Si hay átomos de N en una cadena lineal, la longitud de onda del n-ésimo orbital viene dada por λ = 2nA/n, donde a es la distancia entre átomos.

En este punto, es conveniente definir el número de onda del electrón como k, que tiene unidades de longitud inversa y es inversamente proporcional a λ. k también es directamente proporcional al impulso p. Al igual que p, k es una cantidad vectorial. En un cristal 1D, k puede ser positiva o negativa, correspondiente a un electrón que se mueve hacia la izquierda o derecha a lo largo de la cadena.

\[k = \frac{2\pi}{\lambda} = \frac{2\pi p}{h} \: \: \textrm{where h is Planck's constant}\]

La propiedad más importante de k es que es directamente proporcional al número de nodos n en un orbital molecular dentro de la banda. Para un cristal 1D de átomos de sodio que contiene N celdas unitarias, cada una separada por una distancia a, un orbital molecular con n nodos tiene una longitud de onda λ = 2nA/n y el número de onda k = πN/Na. Podemos ver a partir de esta definición que k = 0 en la parte inferior de la banda (donde λ es infinito) y k = π/a en la parte superior de la banda donde el MO contiene N nodos y λ = 2a.

Energías de orbitales en un cristal metálico

Los electrones con longitudes de onda largas no “sienten” los átomos individuales en la red y así se comportan como si estuvieran casi libres (pero confinados al cristal). Cerca de la parte inferior de la banda, la energía electrónica aumenta parabólicamente con el número de nodos (KE ∝ n ²), ya que el impulso p es directamente proporcional a n. Debido a que p también es directamente proporcional a k, podemos escribir:

\[KE= \frac{p^{2}}{2m} = \frac{h^{2}k^{2}}{8\pi ^ {2}m}\]

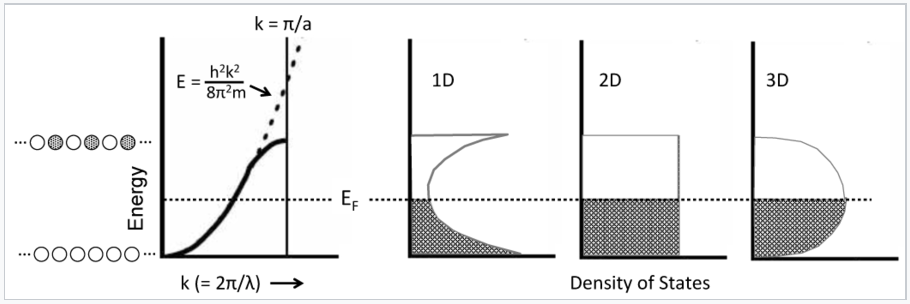
Esta relación parabólica se sigue siempre y cuando la longitud de onda del electrón sea larga en comparación con la distancia entre los átomos. Cerca de la parte superior de la banda, la longitud de onda se acorta y los electrones comienzan a sentir los núcleos atómicos cargados positivamente. En particular, los electrones prefieren tener los máximos en sus ondulaciones alineadas con los núcleos atómicos, que es la situación más favorable electrostáticamente. La atracción electrón-átomo disminuye la energía y hace que la curva E vs. k se desvíe del comportamiento parabólico de un electrón “libre” como se muestra en la siguiente figura.

Densidad de Estados (DOS)

La densidad de estados se define como el número de orbitales por unidad de energía dentro de una banda. Debido a la relación parabólica entre E y k, la densidad de estados para un cristal metálico 1D es mayor cerca de la parte inferior y superior de la banda de energía donde la pendiente de la curva E vs. k es la más cercana a cero. La forma de la curva DOS es diferente en cristales de mayor dimensionalidad como se muestra en la figura de la izquierda, porque estadísticamente hay más formas de hacer un orbital con N/2 nodos que con cero o N nodos. La situación es análoga a los números que puedes hacer rodando dados. Con un dado, los números 1-6 tienen igual probabilidad. No obstante, con dos dados sólo hay una manera de hacer un dos (ojos de serpiente) o un doce (vagones), pero muchas formas de hacer un siete (¡un ganador!).

Los electrones en los metales siguen una curva de dispersión parabólica, donde la energía aumenta con el cuadrado del número de onda, k. Cerca de la parte superior de la banda, la curva de dispersión se desvía de la línea de puntos parabólica. Debido a que hay un MO por cada valor de k, el número de orbitales por unidad de energía (la densidad de estados, DOS) es mayor en la parte inferior y superior de la banda para una cadena 1D de átomos. La densidad de estados es constante con la energía para un cristal 2D, y tiene un máximo en el medio de la banda para un cristal 3D. A baja temperatura, todos los MOs por debajo del nivel de Fermi E F están ocupados, y todos los MOs por encima de él están vacíos.

Si bien la mayor parte del tiempo hablaremos de cristales 3D que tienen su DOS máximo cerca de la mitad de la banda de energía, hay ejemplos de sistemas cuasi-1D, como los nanotubos de carbono. Los nanotubos metálicos de carbono tienen fuertes bandas de absorción óptica que corresponden a transiciones entre las dos regiones de alto DOS (las singularidades de van Hove) cerca de la parte inferior y superior de las bandas.

Los nanotubos de carbono de pared simple con quiralidad “sillón” son metálicos y tienen bandas de absorción afiladas características en el infrarrojo. La Prof. Millie Dresselhaus (abajo) realizó investigaciones fundamentales sobre las propiedades electrónicas de los nanotubos de carbono y otros conductores de baja dimensión.

Metales, semiconductores y aisladores

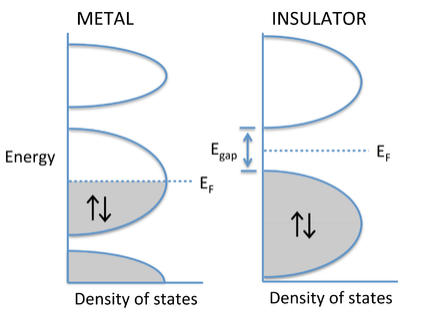
El grado en que se llenan las bandas determina si un sólido cristalino es un metal, semiconductor o aislante. Si los orbitales moleculares más altos ocupados se encuentran dentro de una banda -es decir, si el nivel de Fermi E _F corta a través de una banda de orbitales- entonces los electrones son libres de cambiar su velocidad y dirección en un campo eléctrico y el sólido es metálico. Sin embargo, si el sólido contiene apenas suficientes electrones para llenar completamente una banda, y el siguiente conjunto más alto de orbitales moleculares está vacío, entonces es un semiconductor o aislante. En este caso, existe un hueco de energía entre las bandas llenadas y vacías, las cuales se denominan bandas de valencia y conducción, respectivamente. Aunque la distinción es algo arbitraria, los materiales con una gran brecha (> 3 eV) se denominan aislantes, y aquellos con huecos más pequeños se denominan semiconductores. Aprenderemos más sobre las propiedades de los semiconductores en el Capítulo 10.

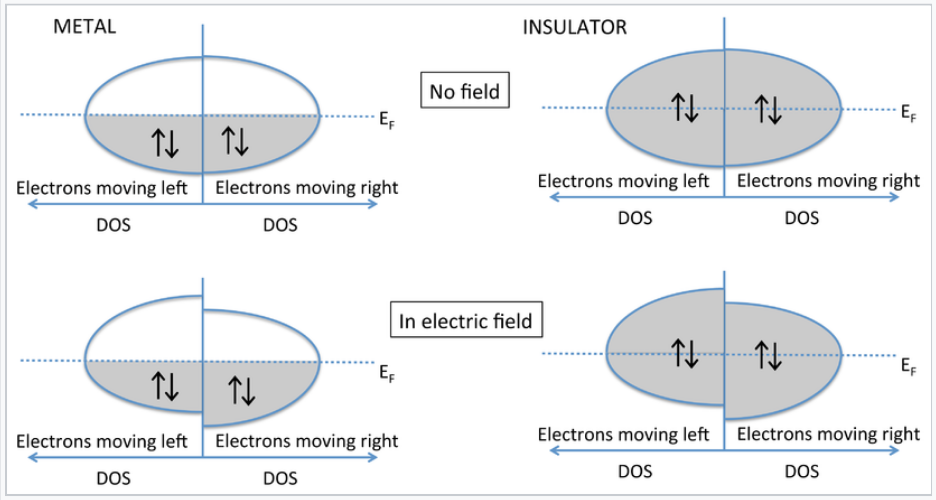
¿Por qué los aislantes no conducen electricidad? El diagrama de energía vs. DOS a continuación muestra lo que sucede cuando se aplica un campo eléctrico a un metal o un aislante. En este caso hemos cambiado el diagrama para mostrar explícitamente las energías de los electrones que se mueven a izquierda y derecha. Estas energías son las mismas en ausencia de un campo eléctrico. Una vez que aplicamos un campo (por ejemplo, poniendo un voltaje a través de un cable metálico), los electrones que se mueven en la dirección del campo tienen menor energía que los que se mueven en la dirección opuesta. En el caso del metal, las poblaciones de electrones que se mueven con y contra el campo eléctrico son diferentes, y hay un flujo neto de corriente. Tenga en cuenta que esto sólo puede suceder cuando el nivel Fermi corta a través de una banda parcialmente llena. Con un semiconductor o aislante, la banda de valencia se llena y la banda de conducción está vacía. La aplicación de un campo eléctrico cambia las energías de los electrones que viajan con y contra el campo, pero debido a que la banda está llena, el mismo número va en ambas direcciones y no hay flujo neto de corriente.

Diagramas E vs DOS que comparan el comportamiento de metales y aislantes en un campo eléctrico aplicado.

Obsérvese que en esta imagen, todos los orbitales moleculares se extienden por todo el cristal. Los electrones de valencia están deslocalizados, incluso en el caso de un semiconductor o aislante. Sin embargo, no puede haber movimiento neto de electrones a menos que la banda esté parcialmente llena.