6.6: Conducción en Metales

En los metales, los electrones de valencia están en orbitales moleculares que se extienden por toda la red cristalina. Como aprenderemos en el Capítulo 7, los metales son casi siempre cristalinos y los granos cristalinos individuales suelen ser de tamaño micrón. Esto significa que la extensión espacial de los orbitales es muy grande en comparación con el tamaño de los átomos o la celda unitaria. El diagrama de la izquierda muestra una gráfica genérica de energía electrónica vs. densidad de estados para un metal como Na, Cu o Ag. En estos casos, hay N orbitales para N electrones, y cada orbital puede acomodar dos electrones. Por lo tanto, el nivel Fermi, que corresponde a la energía del MO ocupado más alto a temperatura cero, se encuentra en algún lugar en la mitad de la banda de orbitales. El espaciamiento del nivel de energía entre orbitales es muy pequeño en comparación con la energía térmica kT, por lo que podemos pensar en los orbitales como formando una banda continua.

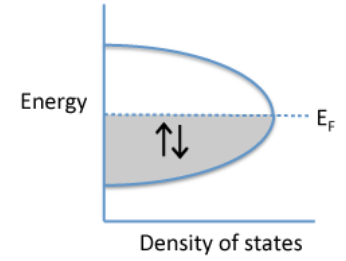
Clásicamente, si los electrones en esta banda fueran libres para ser excitados térmicamente, esperaríamos que tuvieran un calor específico de 3R por mol de electrones. Sin embargo, experimentalmente observamos que C _p es solo de aproximadamente 0.02 R por mol. Esto sugiere que solo alrededor del 1% de los electrones en el metal pueden excitarse térmicamente a temperatura ambiente. Sin embargo, esencialmente todos los electrones de valencia son libres de moverse en el cristal y contribuir a la conducción eléctrica. Para entender esta aparente paradoja, necesitamos recordar que los electrones existen en niveles de energía cuantificados.

Debido a la cuantificación, los electrones en los metales tienen una distribución de energías Fermi-Dirac. En esta distribución, la mayoría de los electrones son espin-pareados, aunque los electrones individuales en estos pares pueden estar bastante separados ya que los orbitales se extienden por todo el cristal. Un número relativamente pequeño de electrones en la cima del mar de Fermi están desapareados por excitación térmica. Este es el origen del paramagnetismo Pauli de los metales.

¿Qué tan rápido viajan los electrones en un metal típico? Debido a la forma de campana de la curva E vs DOS, la mayoría de los electrones tienen E ≈ E _F. En el punto medio de energía (E _F) de la banda, los MO tienen un nodo por cada dos átomos. Podemos calcular la longitud de onda de Broglie como el doble de la distancia entre nodos y así:

λ = 4a en el punto medio de la banda.

donde a es el espaciado interatómico. Dado que un valor típico de a es aproximadamente 2 Å, se obtiene la longitud de onda de Broglie λ ≈ 8 Å.

Usando la relación de Broglie p = h/λ, podemos escribir:

\[\mathbf{p = \frac{h}{\lambda} = m_{e}v_{F}}\]

donde m _e es la masa del electrón y v _F es la velocidad de los electrones con energía E _F.

Resolviendo para\(V_{F} = \frac{h}{m_{e}\lambda}\) que obtengamos\(\mathbf{v_{F}} = \frac{(6.62 \times 10^{-34} J s)}{(9.1 \times 10^{-31} kg)(8 \times 10^{-10}m)} = \mathbf{1.0 \times 10^{6} m/s}\)

Los valores experimentales de v _F son 1.07 x 10 ⁶ y 1.39 x 10 ⁶ m/s para Na y Ag, respectivamente, por lo que nuestras aproximaciones son bastante buenas.

¿Qué tan rápido se mueven los electrones en los metales? De verdad, muy rápido!! ¡1,000,000 metros por segundo! Esto es aproximadamente 1/300 la velocidad de la luz, y alrededor de 3000 veces la velocidad del sonido en el aire (3 x 10 ² m/s).

Sin embargo, la velocidad de deriva de los electrones en los metales -la velocidad a la que los electrones se mueven en el campo eléctrico aplicado- es bastante lenta, del orden de 0.0001 m/s, o .01 cm/s Puede superar fácilmente a un electrón que deriva en un metal, incluso si ha estado bebiendo toda la noche y se ha reducido personalmente a un rastreo muy lento.

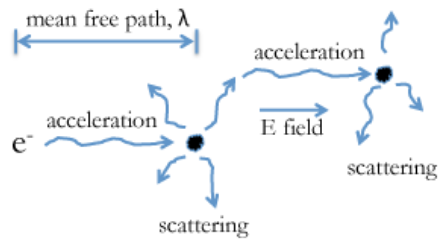
Para comprender la gran disparidad entre la velocidad Fermi y la velocidad de deriva de los electrones en los metales, necesitamos considerar una imagen para la dispersión de electrones, y su aceleración en un campo eléctrico, como se muestra a la izquierda. Si aplicamos un voltaje a través de un metal (por ejemplo, un cable metálico), los electrones se someten a un campo eléctrico E, que es el voltaje dividido por la longitud del cable. Este campo eléctrico ejerce una fuerza sobre el electrón, provocando que se acelere. Sin embargo, el electrón es frecuentemente disperso, principalmente por fonones (vibraciones de celosía). Cada vez que el electrón se dispersa su aceleración comienza de nuevo. El tiempo entre eventos de dispersión es τ y la distancia que viajan los electrones entre eventos de dispersión es la ruta libre media, λ. (Tenga en cuenta que esto NO es la misma λ que la longitud de onda de Broglie, ¡solo que desafortunadamente tienen el mismo símbolo!)

Podemos escribir la fuerza sobre el electrón como:

\[\mathbf{F = eE = m_{e}a = \frac{m_{e}v_{drift}}{\tau}}\]

En esta ecuación, a es la aceleración en el campo eléctrico, m _e es la masa, y v _deriva es la velocidad de deriva del electrón.

Experimentalmente, la trayectoria libre media se obtiene típicamente midiendo el tiempo de dispersión. Para un electrón en metal Cu a 300 K, el tiempo de dispersión τ es de aproximadamente 2 x 10 ^-14 s. A partir de esto podemos calcular la trayectoria libre media como:

\[\mathbf{\lambda = v_{avg}\tau \approx v_{F}\tau} = (1 \times 10^{6} m/s)(2 \times 10^{-14}) = \mathbf{40 nm}\]

La trayectoria libre media (40 nm = 400 Å) es bastante larga en comparación con el espaciamiento interatómico (2 Å). Para ponerlo en perspectiva, si el espaciamiento interatómico se escalara a la longitud de un balón de fútbol (0.3 m), el camino libre medio sería superior a la mitad de la longitud del campo de fútbol (60 m). Así, un electrón recorre un camino bastante largo entre eventos de dispersión y apenas nota la estructura atómica del metal en el que viaja.

Para resumir, los electrones están viajando en metales a la velocidad Fermi v _F, que es muy, muy rápida (10 ⁶ m/s), pero el flujo de electrones es el mismo en todas las direcciones. Es decir, no van a ninguna parte rápido. En un campo eléctrico, se superpone una velocidad de deriva muy pequeña pero direccional sobre este rápido movimiento aleatorio de electrones de valencia.

Para los metales ordinarios, la trayectoria libre media de un electrón de valencia (λ) es bastante larga en relación con el espaciamiento interatómico, representado en esta analogía como la longitud de un balón de fútbol.

Podemos calcular la velocidad de deriva de los electrones como la aceleración en el campo eléctrico multiplicada por el tiempo de dispersión:

A partir de F = ma, obtenemos la aceleración (a) como:

\[\mathbf{a = \frac{F}{m_{e}} = \frac{eE}{m_{e}}}\]

Y así,

\[\mathbf{v_{drift} = a\tau = \frac{eE\tau}{m_{e}}}\]

Si dividimos ambos lados de esta ecuación por la magnitud del campo eléctrico (E), obtenemos la movilidad (μ):

\[\mathbf{\mu=\frac{v_{drift}}{E}= \frac{e\tau}{m_{e}}}\]

μ tiene unidades de velocidad/campo = cm/s/V/cm = cm ² /Vs

Una consecuencia importante del cálculo de la _deriva v es la Ley de Ohm, V = iR. De las ecuaciones anteriores, podemos ver que la velocidad de deriva aumenta linealmente con el campo eléctrico aplicado. La velocidad de deriva (cm/s) es proporcional a la corriente (i, coul/s), y el campo eléctrico (E, V/cm) es proporcional a la tensión (V):

\[\mathbf{Current \: (i) = nev_{drift} \times area}\]

\[\mathbf{Voltage \: (V) = E \times length}\]

Aquí n es la densidad de los electrones de valencia (#/cm ³) y e es la carga del electrón (coul). Combinando estas ecuaciones con nuestra ecuación para v _drift obtenemos:

\[V = i(\frac{m_{e}}{ne^{2}\tau})\frac({length}{area}) = iR\]

Así, V = iR, donde R es la combinación de los dos términos entre paréntesis. El primero de ellos es la resistividad\(\rho\), y el segundo es un factor geométrico.

La conductividad (σ) de un metal, que es la inversa de\(\rho\), es proporcional a μ, que a su vez es proporcional a τ (y λ):

\[\mathbf{\sigma = ne\mu = \frac{ne^{2}\tau}{m_{e}}}\]

Podemos usar esta ecuación para calcular la conductividad de un metal específico (Cu), para lo cual n = 8.5 x 10 ²² cm ^-3 y τ = 2 x 10 ^-14 s. Poniendo los números para m _{e y e}, obtenemos σ = 7 x 10 ⁵ Ω ^{-1 cm -1} cm ^-1 para Cu, en buena acuerdo con el valor medido (6 x 10 ⁵ Ω ^-1 cm ^-1).