9.6: Descubrimiento de compuestos de gases nobles

Última actualización
Guardar como PDF

Page ID: 72181

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

En 1962 en la Universidad de Columbia Británica, Neil Bartlett estaba trabajando con el potente oxidante PtF ₆ y, debido a una fuga accidental en su línea de vacío, notó la reacción del compuesto con O ₂ para generar un sólido con fórmula “PtF ₆ O ₂”. La fórmula sugería Pt en el estado de oxidación +10, lo cual fue claramente irrazonable porque se sabía que PtF ₆ era un oxidante más potente que el flúor molecular (F ₂) o el oxígeno molecular (O ₂). Bartlett notó que el patrón de difracción de rayos X en polvo del compuesto fue similar al de Cs ⁺ AsF ₆ ^-, una sal con la estructura CsCl en la que los iones octaédricos AsF ₆ ^- ocupan los sitios de iones cloruro. Esto llevó a Bartlett a proponer una formulación de O ₂ ⁺ PtF ₆ ^- para su nuevo compuesto. ^[6] Los datos de susceptibilidad magnética confirmaron posteriormente la presencia del catión paramagnético O ₂ ⁺, el cual (ver Capítulo 2) tiene un orden de enlace de 2.5. Esta formulación implica que PtF ₆ era un agente oxidante lo suficientemente fuerte como para oxidar el oxígeno molecular.

Pero ¿qué tan fuerte es un oxidante PtF ₆? Su afinidad electrónica podría estimarse usando un ciclo Born-Haber, llenando la energía reticular de O ₂ ⁺ PtF ₆ ^- por medio de la fórmula de Kapustinskii:

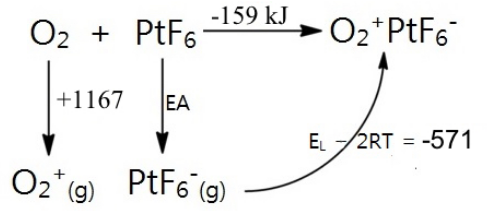
La afinidad electrónica (EA) para PtF ₆ se puede calcular como EA = -159 - 1167 + 571 = -751 kJ/mol. Para ponerlo en perspectiva, esto es 417 kJ/mol más exotérmico que la afinidad electrónica del flúor atómico (334 kJ). ¡PtF ₆ fue, con mucho, el oxidante más fuerte que se había hecho nunca!

Cristales de difluoruro de xenón (XeF ₂), el cual se elabora por fotólisis de una mezcla gaseosa de Xe y F ₂. XeF ₂ se utiliza como agente de ataque selectivo para SiO ₂ en ciertos procesos de fabricación microelectrónica. Antes de que Neil Bartlett descubriera el primer compuesto de xenón en 1962, se creía que los elementos del grupo VIII (He, Ne, Ar, Kr, Xe) no podían formar compuestos químicos. Desde entonces, los químicos han descubierto una rica familia de compuestos de gases nobles que contienen Xe, Kr o Ar.

Bartlett reconoció que Xe tiene energía de ionización de +1170 kJ, que está muy cerca de la energía de ionización de O ₂. Dado que Xe ⁺ debe ser aproximadamente del mismo tamaño que O ₂ ⁺, la energía reticular debe ser aproximadamente la misma con Xe ⁺ en el sitio catiónico de la estructura O ₂ ⁺ PtF ₆ ^-. Dado que todos los demás términos en el ciclo Born-Haber para la reacción de Xe con PtF ₆ son los mismos, Bartlett concluyó que Xe ⁺ PtF ₆ ^-, como O ₂ ⁺ PtF ₆ ^-, debería ser un compuesto estable. Compró una botella de conferencia de gas xenón y reaccionó los dos compuestos, produciendo un sólido naranja. ^[7] Si bien el producto inicialmente formado en la reacción puede ser de hecho Xe ⁺ PtF ₆ ^-, el radical libre Xe ⁺ es un potente ácido de Lewis y reacciona más con el exceso de PtF ₆. El producto final de la reacción se formula [XeF ⁺] [Pt ₂ F ₁₁ ^-], una sal que contiene Xe en el estado de oxidación +2 y Pt en el estado de oxidación +5. Este fue un descubrimiento importante porque destrozó la noción dogmática, que derivaba de la regla del octeto, de que los elementos del grupo VIII no podían formar vínculos con otros elementos. El nombre de este grupo se cambió de los “gases inertes” a los “gases nobles”. Posteriormente, se sintetizaron y caracterizaron muchos compuestos de Xe y algunos de Kr e incluso Ar (que es mucho más difícil de oxidar).