1.8:Sistemas cíclicos N-dimensionales

Última actualización
Guardar como PDF

Page ID: 74682

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Esta conferencia proporcionará una derivación de las funciones propias de LCAO y los valores propios de N número total de orbitales en una disposición cíclica. El problema se ilustra a continuación:

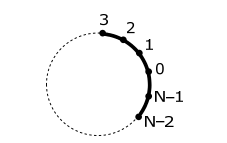
Hay dos derivaciones a este problema.

Derivación polinomial

El determinante de Hückel viene dado por,

\ [D_ {N} (x) =\ izquierda|\ begin {array} {ccccccccc}
x & 1 & & & & & & & & & & & &\
1 & & & & & & & & & & & &
&\\ & 1 & x &\ ddots & & & & & &
&\\ & 1 &\ ddots &\ ddots & & & &\ &
& &\ ddots &\ ddots &\ ddots &\ ddots & & & &
& &\ ddots &\ ddots &\ ddots &\ ddots &\ ddots
&\ ddots &\ ddots &\ ddots &\\ ddots &\\
& & ; & & & &\ ddots & x & 1\\
& & & & & & & & & 1 & x
\ end {matriz}\ derecha|=0\]

donde

\[ x=\frac{\alpha-E}{\beta}\]

De una expansión de Laplace se encuentra,

D _N (x) = xD _n _-1 (x) - D _N-2 (x)

Dónde

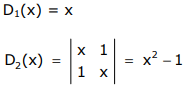
Con estos parámetros definidos, se puede obtener la forma polinómica de D _N (x) para cualquier valor de N,

D ₃ (x) = xD ₂ (x) — D ₁ (x) = x (x ² —1) — x = x (x ² —2)

D ₄ (x) = xD ₃ (x) — D ₂ (x) = x ² (x ² —2) — (x ² —1)

\[ \vdots \nonumber \]

y así sucesivamente

La expansión de DN (x) tiene como solución,

\[ x={-2}\cos \dfrac{2\pi}{N}j (j= 0, 1, 2, 3...N-1) \nonumber \]

y sustituyendo x,

\[ E = \alpha + 2\beta\cos \dfrac{2\pi}{N}j (j= 0, 1, 2, 3...N-1) \nonumber \]

Derivación de onda estacionaria

Un enfoque alternativo para resolver este problema es expresar la función de onda directamente en una coordenada angular, θ

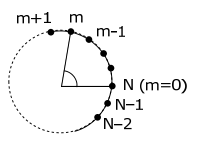
Para una onda estacionaria de λ alrededor del perímetro de un círculo de circunferencia c,

\[ \psi_j = \sin \dfrac{c}{\lambda} \theta \nonumber \]

La solución a la función de onda debe ser de valor único. Se debe obtener una sola solución para ψ a cada 2nπ o en términos analíticos,

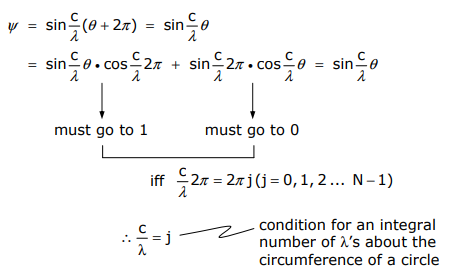
Así, la amplitud de$ψ_j$ at átomo m es, (donde c/λ = j y θ = (2π/N) m)

\[ \psi_{j}(m) = \sin{2m\pi}{N}j (j= 0, 1, 2, 3...N-1) \nonumber \]

Dentro del contexto del método LCAO, ψ _j puede reescribirse como una combinación lineal en φ _m con coeficientes _cjm. Así, la amplitud de ψ _j a m es equivalente al coeficiente de φ _m en la expansión LCAO,

\[ \psi_{j} = \displaystyle \sum_{k=1}^N C_{jm\phi m} \]

Dónde

\[C_{jm} = \sin{2\pi m}{N}j (j= 0, 1, 2, 3...N-1) \nonumber \]

La energía de cada MO, ψ _j, puede determinarse a partir de una solución de la ecuación de Schrödinger,

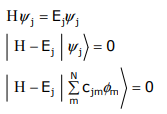
La energía del orbital φ _m se obtiene por izquierda—multiplicando por φ _m,

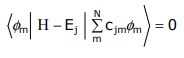
pero se impone la condición de Hückel; los únicos términos que se conservan son los que involucran φ _m, φ _m ₊₁ y φ _m _-1. Ampliando,

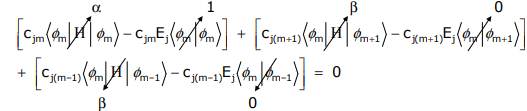
Evaluando las integrales,

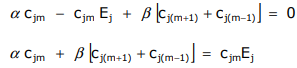
Sustituyendo por c _jm,

\[ \alpha \sin \dfrac{2\pi m}{N}j + \beta \left( \sin \dfrac{2\pi (m+1)}{N}j + \sin \dfrac{2\pi (m-1)}{N}j \right) = E_{j} \sin \dfrac{2\pi m}{N}j \nonumber \]

\[ \alpha + \dfrac{ \beta \left( \sin \dfrac{2\pi (m+1)}{N}j + \sin \dfrac{2\pi (m-1)}{N}j \right)}{ \sin \dfrac{2\pi m}{N}j} = E_{j} \nonumber \]

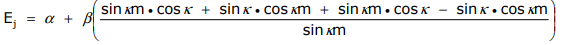
\[ E_{j} = \alpha + 2\beta \cos k \nonumber \]

\[ E_{j} = \alpha + 2\beta \cos \dfrac{2\pi}{N}j (j= 0, 1, 2, 3...N-1) \nonumber \]

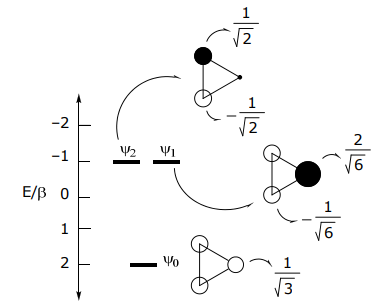
Veamos el sistema cíclico más simple, N = 3

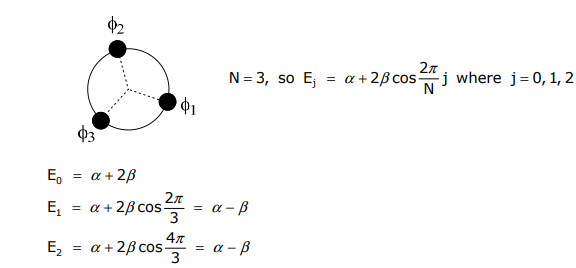
Continuando con nuestro enfoque (LCAO) y usando Ej para resolver para la función propia, encontramos...

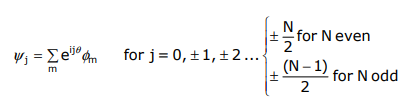
Usando la expresión general para ψ j, las funciones propias son:

\[ \psi_{0} = e^{i(0)0} \phi_{1} + e^{i(0) \dfrac{2\pi}{3}} \phi_{2} + e^{i(0) \dfrac{4\pi}{3}} \phi_{3} \nonumber \]

\[ \psi_{1} = e^{i(1)0} \phi_{1} + e^{i(1) \dfrac{2\pi}{3}} \phi_{2} + e^{i(1) \dfrac{4\pi}{3}} \phi_{3} \nonumber \]

\[ \psi_{-1} = e^{i(-1)0} \phi_{1} + e^{i(-1) \dfrac{2\pi}{3}} \phi_{2} + e^{i(-1) \dfrac{4\pi}{3}} \phi_{3} \nonumber \]

Obtención de componentes reales de las funciones de onda y normalización,

$$
\ begin {array} {ll}
\ psi_ {0} =\ phi_ {1} +\ phi_ {2} +\ phi_ {3}\ rightarrow &\ psi_ {0} =\ frac {1} {\ sqrt {3}}\ left (\ phi_ {1} +\ phi_ {2} +\ phi_ {3}\ derecha)\
\ psi_ {+1} +\ psi_ {-1} =2\ phi_ {1} -\ phi_ {2} -\ phi_ {3}\ fila derecha &\ psi_ {1} =\ frac {1} {\ sqrt {6}}\ izquierda (2\ phi_ {1} -\ phi_ {2} -\ phi _ {3}\ derecha)\
\ psi_ {+1} -\ psi_ {-1} =\ phi_ {2} -\ phi_ {3}\ fila derecha &\ psi_ {2} =\ frac {1} {\ sqrt {2}}\ izquierda (\ phi_ {2} -\ phi_ {3}\ derecha)
\ end {array}
\]

Resumiendo en un diagrama MO donde α se establece igual a 0,