1.12: Complejos Octaédricos ML6-Sigma

Última actualización
Guardar como PDF

Page ID: 74690

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Un complejo octaédrico comprende un ión metálico central y seis ligandos terminales. Si los ligandos son exclusivamente donadores σ, entonces el conjunto de bases para los ligandos se define de la siguiente manera:

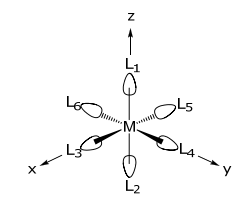
Los ligandos que se mueven tras la aplicación de una operación, R, no pueden contribuir al elemento de matriz diagonal de la representación. Dado que el enlace σ está a lo largo del eje internuclear que conecta el ligando y el metal, las propiedades de transformación del ligando son correspondientes a las del enlace M—L σ. Además, un enlace σ no tiene cambio de fase dentro del eje internuclear, de ahí que el enlace solo pueda transformarse en sí mismo (+1) o en otro ligando (0).

\ begin {array} {c|cccccccccc}
\ mathrm {O} _ {\ mathrm {h}} &\ mathrm {E} &\ mathrm {8C} _ {3} & 6\ mathrm {C} _ {2} & 6\ mathrm {C} _ {4} & 3\ mathrm {C} _ {2}\ left (=\ mathrm {C} _ {4} {} ^ {2}\ derecha) &\ mathrm {i} & 6\ mathrm {~S} _ {4} & 8\ mathrm {~S} _ {6} & 3\ sigma_ {\ mathrm {h}} & 6\ sigma_ {\ mathrm {d}}\
\ hline\ Gamma_ {\ mathrm {L}\ sigma} & 6 & 0 & 0 & 2 & 0 & 0 & 0 & 0 & 0 & 4 & 2
\ end {array}

\[\Gamma_{\mathrm{L} \sigma}=\mathrm{a}_{1 \mathrm{~g}}+\mathrm{t}_{1 \mathrm{u}}+\mathrm{e}_{\mathrm{g}}\]

Ahora es necesario determinar las SALC del conjunto de bases Lσ. Tres métodos diferentes entregarán las SALC.

Método 1

Como hemos hecho anteriormente, las SALC de Lσ se pueden determinar utilizando el operador de proyección. Obsérvese que el ligando que se mezcla en O _h se retiene en el subgrupo rotacional puro, O. Puede así caer de O _h → O, ahorrando así 24 operaciones.

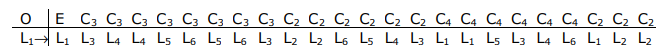
La representación irreducible A ₁ es totalmente simétrica. De ahí que la proyección sea simplemente la suma de las transformaciones de ligandos anteriores.

P ^{A ₁} (L1) ~ 4 (L1 + L2 + L3 + L4 + L5 + L6)

y normalizar los rendimientos,

\ (
\ psi_ {a_ {19}} =\ frac {1} {\ sqrt {6}}\ left (\ mathrm {~L} _ {1} +\ mathrm {L} _ {2} +\ mathrm {L} _ {3} +\ mathrm {L} _ {4} +\ mathrm {L} _ {5} +\ mathrm {L} _ {6}\ right)\)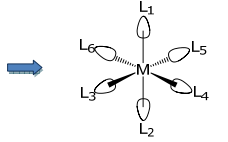
La aplicación del operador de proyección para la representación irreducible E proporciona las SALC E _g.

\ (\ comenzar {alineado}
P^ {E}\ izquierda (L_ {1}\ derecha) &\ fila derecha\ izquierda (2 L_ {1} -L_ {3} -L_ {4} -L_ {4} -L_ {5} -L_ {6} -L_ {5} -L_ {6} -L_ {3} +2 L_ {1} +2 L_ {2} +2 L_ {2} +2 L_ {2} +2 L_ {2} +2 L_ {2} +2 L_ {2} +2 L_ {2} +2}\ derecha)\\
&\ fila derecha\ izquierda (4 L_ {1} +4 L_ {2} -2 L_ {3} -2 L_ {4} -2 L_ {5} -2 L_ {6}\ derecha)
\ final {alineado}\)

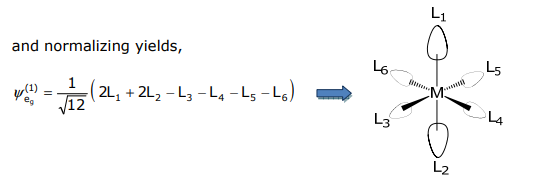
Pero E _g es una representación doblemente degenerada, y por lo tanto hay otra SALC. Como es obvio desde arriba, el operador de proyección sólo produce una de las dos SALC. ¿Cómo obtenemos el otro?

Método 2

El procedimiento de ortogonalización de Schmidt puede extraer las SALC de una combinación lineal no ortogonal de una base apropiada. Supongamos que tenemos un SALC, v ₁, entonces existe un v ₂ que cumple con la siguiente condición,

v ₂ = a v ₁ + u

donde u es la combinación lineal no ortogonal. Multiplicar la ecuación anterior por v ₁ da,

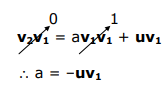
¿Cuál es la naturaleza de u? Considere usar el operador de proyección en L ₃ en lugar de L ₁,

\[\mathrm{P}^{\mathrm{e}_{9}}\left(\mathrm{~L}_{3}\right)=\frac{1}{\sqrt{12}}\left(2 \mathrm{~L}_{3}+2 \mathrm{~L}_{5}-\mathrm{L}_{1}-\mathrm{L}_{2}-\mathrm{L}_{4}-\mathrm{L}_{6}\right)\]

Tenga en cuenta que esto no arroja ninguna nueva información, es decir, los orbitales atómicos en un eje son el doble de eso y están desfasados de los orbitales atómicos en el plano ecuatorial. Sin embargo, esta nueva función de onda no es ψ _eg ⁽²⁾ porque no es ortogonal a ψ _eg ⁽¹⁾.

Así, la proyección debe producir una función de onda que sea una combinación lineal de ψ _eg ⁽¹⁾ y ψ _eg ⁽²⁾, es decir, la función de onda obtenida de la proyección es una u viable. Aplicando el procedimiento de ortogonalización de Schmidt,

\ [\ begin {alineado}
a &=-\ mathbf {u v} _ {1} =-\ izquierda\ langle\ frac {1} {\ sqrt {12}}\ izquierda (2 L_ {3} +2 L_ {5} -L_ {1} -L_ {2} -L_ {4} -L_ {6}\ derecha)\ mediados\ frac {1} {\ sqrt {12}}\ izquierda (2 L_ {1} +2 L_ {2} -L_ {3} -L_ {4} -L_ {5} -L_ {6}\ derecha)\ derecha\ rangle\\
&=-\ frac {1} {12} [-6] =+\ frac {1} {2}
\ end { alineado}\]

entonces,

\ [\ begin {alineado}
\ mathbf {v} _ {2} &=\ frac {1} {2}\ frac {1} {\ sqrt {12}}\ izquierda (2 L_ {1} +2 L_ {2} -L_ {3} -L_ {4} -L_ {5} -L_ {6}\ derecha) +\ frac {1} {\ sqrt {12}}\ izquierda (2 L_ {3} +2 L_ {5} -L_ {1} -L_ {2} -L_ {4} -L_ {6}\ derecha)\\
&=\ frac {1} {\ sqrt {12}}\ izquierda [\ izquierda (\ frac {3} {2} L_ {3} +\ frac {3} {2} L_ {5} derecha) -\ left ( \ frac {3} {2} L_ {4} +\ frac {3} {2} L_ {6}\ derecha)\ derecha]\ aprox\ izquierda (L_ {3} +L_ {5}\ derecha) -\ izquierda (L_ {4} +L_ {6}\ derecha)
\ final {alineado}\]

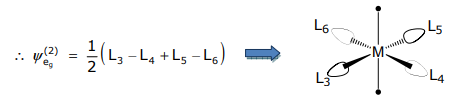
ψ _eg ⁽²⁾ es ortogonal a ψ _eg ⁽¹⁾, así es el otro SALC.

Ahora se deben determinar las SALC T _1g. El operador de proyección rinde,

_{P ^{T ₁} (L ₁) → (3L ₁ — L ₂ — L ₂ — L ₆ — L ₅ — L ₄ — L ₃ + L 1 + L ₁ + L ₅ + L ₃ + L ₄ + L 6 — L ₆ — L} ₁ — L ₁ — L ₂)

P ^{T ₁} (L ₁) ~ 3 (L ₁ — L ₂)

y normalizar los rendimientos,

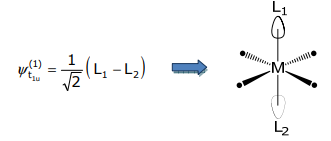
Aplicando el método de ortogonalización de Schmidt,

$$
\ mathrm {P} ^ {\ mathrm {T} _ {1}}\ izquierda (\ mathrm {~L} _ {3}\ derecha)\ sim 3\ izquierda (\ mathrm {~L} _ {3} -\ mathrm {L} _ _ {5}\ derecha)\ derecha)\ derecha\ psi_ {\ mathrm {t} _ {\ mathrm {lu}} = frac {1} {\ sqrt {2}}\ izquierda (\ mathrm {~L} _ {3} -\ mathrm {L} _ _ {5}\ derecha)
\]

Esta función de onda es ortogonal a ψ _{^t 1u} ⁽¹⁾, de ahí que sea probablemente una SALC. Puede probarlo mediante t1u aplicando el proceso de ortogonalización de Schmidt y configurando esto para que sea u. Resolviendo para a,

$$
\ begin {aligned}
a &=-\ mathbf {u}\ mathbf {v} _ {1} =-\ izquierda\ langle\ frac {1} {\ sqrt {2}}\ izquierda (\ mathrm {~L} _ {1} -\ mathrm {L} _ _ {2}\ derecha)\ mid\ frac {1} {\ sqrt {2}}\ izquierda (\ mathrm {~L} _ {3} -\ mathrm {L} _ {5}\ derecha)\ derecha\ rangle\\
&=-\ frac {1} {2} (0) =0
\ end {alineado}
\]

$$
v_ {2} =a v_ {1} +u=0\ cdot\ frac {1} {\ sqrt {2}}\ izquierda (L_ {1} -L_ {2}\ derecha) +\ frac {1} {\ sqrt {2}}\ izquierda (L_ {3} -L_ {5}\ derecha)
\]

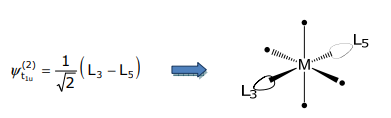
entonces, como se sospechaba, se trata de una SALC. Y el tercer SALC de simetría T _1u es el par (L ₄, L ₆).

Método 3

Para aquellas SALC con simetrías que son las mismas que los orbitales s, p o d, pueden adaptar la simetría del conjunto de ligandos a la simetría de los orbitales metálicos.

Considera el orbital dz2, que se define con mayor precisión como 2z ² — x ² — y ². Así, el coeficiente del eje z es el doble que el de x e y y desfasado con x e y, por lo tanto, los ligandos en el eje z, L ₁ y L ₂, deben ser el doble que y de signo opuesto a los ligandos ecuatoriales, L ₃, L ₄, L ₅, L ₆. Esto conduce naturalmente a,

$$
\ begin {alineado}
&\ psi_ {\ mathrm {e} _ {9}} ^ {(1)}\ approx 2\ mathrm {~L} _ {1} +2\ mathrm {~L} _ {2} -\ mathrm {L} _ {3} -\ mathrm {L} _ {4} -\ mathrm {L} _ {5} -\ mathrm {L} _ {6}\\
&\ psi_ {\ mathrm {e} _ {9}} ^ {(1)} =\ frac {1} {\ sqrt {12}}\ left (2\ mathrm {~L} _ _ {1} +2\ mathrm {~L} _ {2} -\ mathrm {L} _ {3} -\ mathrm {L} _ {4} -\ mathrm {L} _ {5} -\ mathrm {L} _ _ {6}\ derecha)
\ final {alineado}
\]

El otro SALC de este conjunto degenerado viene dado por d _{x ²} _{—y ²}, que no tiene coeficiente sobre z, y x e y coeficientes que son iguales pero de signo opuesto. Por simetría coincidente con la órbita,

$$
\ begin {alineado}
&\ psi_ {\ mathrm {e} _ {9}} ^ {(2)}\ approx\ mathrm {L} _ {3} -\ mathrm {L} _ {4} +\ mathrm {L} _ {5} -\ mathrm {L} _ _ {6}\
&\ psi_ {\ mathrm {e} _ {9}} ^ (2)} =\ frac {1} {2}\ izquierda (\ mathrm {~L} _ {3} -\ mathrm {L} _ {4} +\ mathrm {L} _ {5} -\ mathrm {L} _ _ {6}\ derecha)
\ end {alineado}
\]

Las otras SALC siguen su ejemplo.

El conjunto _t-2g d-orbital (es decir, d _xy, d _xz, d _yz) es de simetría incorrecta para interactuar con el conjunto de ligandos Lσ y, por lo tanto, no se une. Esto se puede ver a partir de la imagen orbital. Los orbitales Lσ se dirigen entre los lóbulos de los t _2g d-orbitales,

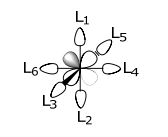
Solo los orbitales metálicos y las SALC de la misma simetría pueden superponerse. En el caso del complejo octaédrico ML ₆ σ-complejo,

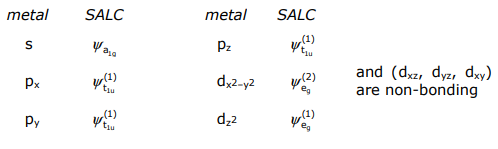
Teniendo en cuenta las consideraciones anteriores de ΔE _ML _{y S ML}, el diagrama MO para M (Lσ) ₆ se construye con Co (NH ₃) ₆ ³⁺ como modelo,

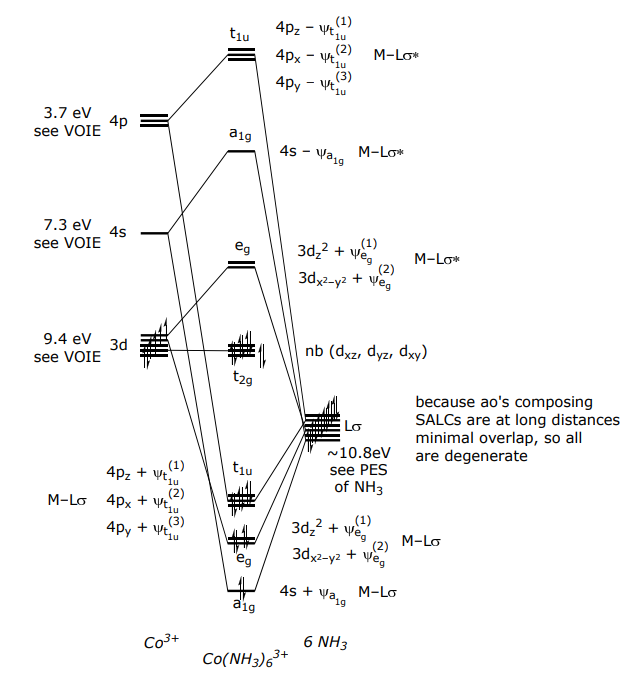
Las energías de interacción ε _σ y ε _σ _* (es decir, los elementos de la matriz fuera de la diagonal, _HML) son menores que la diferencia en las energías de los orbitales atómicos de metal y ligando (es decir, los elementos de la matriz diagonal, H _MM y H _LL), por lo que molecular los orbitales permanecen dentro de sus “zonas” energéticas.