2.2.1: Partícula en una Caja
- Page ID
- 81223
La partícula en la caja es un modelo que puede ilustrar cómo funciona una ecuación de onda. Aunque no representa una situación real, podemos limitar nuestro modelo a una sola dimensión (la dimensión x, por ejemplo) de tal manera que la ecuación de Schrödinger se simplifica significativamente. A pesar de ser poco realista, esta simplificación es bastante útil para comprender la ecuación de Schrödinger.
El modelo de una partícula en una caja
La partícula en la caja es una situación hipotética con una partícula atrapada en una “caja” unidimensional. No nos colguemos en el hecho de que el objeto común llamado “caja” suele ser un objeto con tres dimensiones en lugar de una sola dimensión. Y tampoco nos colguemos de la palabra “partícula”. Esta es una partícula que tiene propiedades de una onda... así que es diferente a la partícula macroscópica que probablemente estés imaginando. Esta “caja” es más como una línea, o un eje x; es solo un espacio unidimensional en el que queda atrapada una onda de partículas.
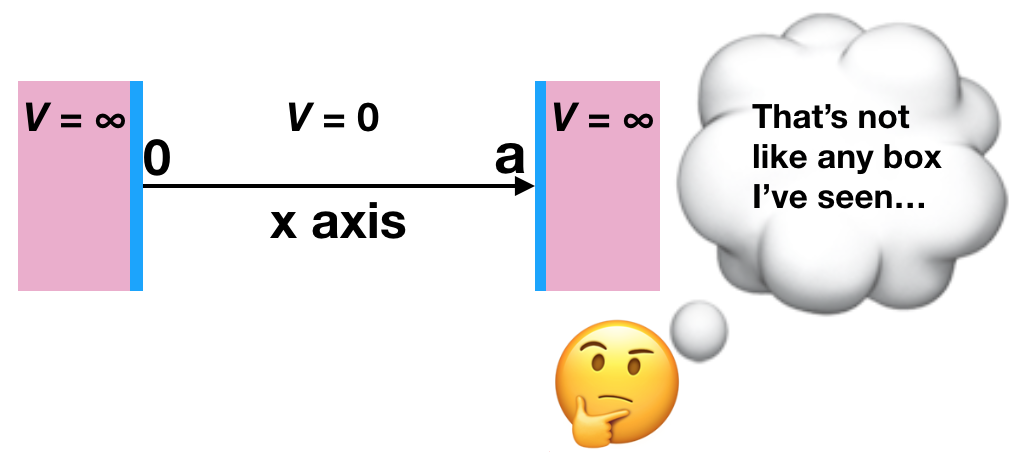
La onda de partículas solo puede existir dentro de las paredes (donde\(0<x<a\)), a lo largo del eje x en la figura que se muestra arriba. En términos de energía, la energía potencial es cero (\(V=0\)) porque la partícula se encuentra en una posición energéticamente favorable aquí. Por otro lado, fuera de la caja, la partícula no puede existir y la energía potencial es infinitamente grande (\(V=\infty\)) fuera de las paredes (donde\(x<0\) o\(x>a\)). Esto significa que es infinitamente desfavorable que la onda de partículas exista fuera de la caja, y así nunca lo hace. La onda de partículas queda atrapada entre las paredes, a lo largo del\(x\) eje unidimensional, y no hay fuerzas que actúen sobre la onda de partículas dentro de esta “caja”.
La ecuación de onda de Schrödinger para una partícula en una caja
El modelo de partículas en caja nos permite considerar una versión simple de la ecuación de Schr ö dinger. Antes de simplificar, echemos otro vistazo al Hamiltoniano completo para una onda de partículas en tres dimensiones (ver ecuación 2.2.2) y la forma más simple de la ecuación de Schrödinger (ver ecuación 2.2.1). Ambas ecuaciones se describen en la sección anterior y se escriben a continuación para mayor comodidad.
La ecuación de Schrödinger (de la ecuación 2.2.1):\(\hat{H}\psi = E\psi\)
El hamiltoniano en tres dimensiones (de la ecuación 2.2.2):
\[\hat{H}=\dfrac{-h{^2}}{8\pi{^2}m_e}\left(\dfrac{\partial{^2}}{\partial{x^2}}+\dfrac{\partial{^2}}{\partial{y^2}}+\dfrac{\partial{^2}}{\partial{z^2}}\right)-\dfrac{Ze^2}{4\pi{}\epsilon_0{r}}\nonumber \]
En la partícula en un modelo de caja, sólo hay una dimensión,\(x\). Debido a que los\(z\) valores\(y\) y son cero, podemos caer\(y\) y\(z\) salir de nuestra ecuación hamiltoniana. Y, ya que\(V=0\) dentro de la caja, podemos dejar caer toda la parte de la ecuación hamiltoniana que describe la energía potencial (\(\frac{-Ze^2}{4\pi{}\epsilon_0{r}}\)). Esto nos deja con un operador hamiltoniano muy simplificado, que luego podemos usar para escribir la ecuación de onda de Schrödinger para una partícula que se mueve en una dimensión. Una última cosa que haremos es usar un valor más general\(m\) para la masa de la partícula, en lugar de\(m_e\) que eso represente específicamente la masa de un electrón. La ecuación de Schrödinger para una onda de partículas en una caja unidimensional es:
\[\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}\psi(x)}{\partial{x^2}}\right) = E\psi \label{1DSchr} \]
Siga los pasos que se describieron en el último párrafo para encontrar la Ecuación\ ref {1DSChR} de las ecuaciones 2.2.1 y 2.2.2. En otras palabras, derivar la Ecuación de Schr ö dinger para la partícula en una caja dada las ecuaciones tridimensionales Hamiltoniana y Schr ö dinger.
- Contestar
-
Aquí está la Ecuación Hamitlónica para en tres dimensiones.
\(\hat{H}=\textcolor{red}{\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}}{\partial{x^2}}+\dfrac{\partial{^2}}{\partial{y^2}}+\dfrac{\partial{^2}}{\partial{z^2}}\right)}-\textcolor{blue}{\dfrac{Ze^2}{4\pi{}\epsilon_0{r}}}\)
Hay dos partes en esta ecuación: la contribución de energía cinética y la contribución de energía potencial. Si bien la primera parte de esta expresión,\(\textcolor{red}{\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}}{\partial{x^2}}+\dfrac{\partial{^2}}{\partial{y^2}}+\dfrac{\partial{^2}}{\partial{z^2}}\right)}\), es el aporte de energía cinética, la segunda parte de la expresión,\(\textcolor{blue}{-\dfrac{Ze^2}{4\pi{}\epsilon_0{r}}}\), es la contribución de energía potencial (\(V\)).
(1) Simplificar la expresión de energía cinética
Tu onda de partículas se mueve en una sola dimensión. Podemos elegir arbitrariamente la dimensión\(x\). Esto quiere decir que\(x\) es una variable y tendrá algún valor de\(0\) a\(a\). Por otro lado, la partícula no se mueve en las otras dos dimensiones,\(y\) y\(z\). Puedes asignar la posición de la partícula a lo largo\(x\) y\(y\) los ejes como cero o simplemente puedes entender que no existen en ninguna capacidad significativa en nuestro espacio 1-D. De cualquier manera, puedes simplemente dejarlos fuera de la parte de energía cinética del hamiltoniano, así:
Cuando\(y=z=0\) y la onda de partículas solo existe/se mueve en la\(x\) dimensión,\(\textcolor{red}{\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}}{\partial{x^2}}+\dfrac{\partial{^2}}{\partial{y^2}}+\dfrac{\partial{^2}}{\partial{z^2}}\right)}\) =\(\textcolor{red}{\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}}{\partial{x^2}}\right)}\)
Y el hamiltoniano general se simplifica:
\(\hat{H}=\textcolor{red}{\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}}{\partial{x^2}}\right)}-\textcolor{blue}{\dfrac{Ze^2}{4\pi{}\epsilon_0{r}}}\)
(2) Simplificar la expresión de energía potencial (\(V\)).
La energía potencial de la partícula dentro de la caja es cero (\(V=0\)). Por lo tanto,\(\textcolor{blue}{V=-\dfrac{Ze^2}{4\pi{}\epsilon_0{r}}}=0\). Simplemente podemos dejar caer la porción de energía potencial del hamiltoniano porque su valor es cero.
El hamiltoniano simplificado es ahora:
\(\hat{H}=\textcolor{red}{\dfrac{-h^2}{8\pi^2m}\left(\dfrac{\partial{^2}}{\partial{x^2}}\right)}\)
(3) Sustituir el hamiltoniano simplificado por la Ecuación Schr ö dinger.
El Schr ö dinger es:\(\textcolor{red}{\hat{H}}\psi = E\psi\)
Cuando el hamiltoniano simplificado se sustituye en esta ecuación, el resultado es la Ecuación 1-D Schr ö dinger\ ref {1dSchR}.
\(\textcolor{red}{\left(\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}\psi(x)}{\partial{x^2}}\right)\right)} = E\psi\)
La función de onda de una onda unidimensional
Aunque hemos simplificado la Ecuación de Schrödinger al considerar la partícula en la caja, la Ecuación\ ref {1DSChR} aún puede parecerle misteriosa. Pero es más sencillo de lo que te darías cuenta. ¡Vamos a desempacarlo! Aquí vamos a pasar por los pasos de derivar la función de onda unidimensional para la partícula en una caja. No intentaremos derivar una función de onda tridimensional para un electrón “real”, pero cuando entiendas cómo encontrar la función de onda unidimensional, y lo que nos dice, entonces puedes extender conceptualmente esto para entender lo que la función de onda nos dice sobre los electrones en tres dimensiones.
Vamos a diseccionar la Ecuación\ ref {1DSChR}. Aquí vuelve a ser de referencia:
\[\textcolor{green}{\dfrac{-h{^2}}{8\pi{^2}m_e}}\left(\dfrac{\partial{^2}\psi(x)}{\partial{x^2}}\right) = \textcolor{green}{E}\psi\nonumber \]
La expresión\(\textcolor{green}{\frac{-h^2}{8\pi^2m_e}}\) es sólo una constante negativa. Esta constante negativa se multiplica por la segunda derivada de la función de onda en la expresión anterior. Y\(\textcolor{green}{E}\) es una constante multiplicada por esa misma función. Podemos reorganizar esta ecuación de la siguiente manera:
\[\dfrac{\partial{^2}\psi(x)}{\partial{x^2}} = \textcolor{green}{\dfrac{-8\pi{^2}m_eE}{h{^2}}}\psi = -\textcolor{green}{C}\psi \label{Schrx} \]
donde\(C\) es solo la constante;\(\textcolor{green}{C}=\textcolor{green}{\dfrac{8\pi{^2}m_eE}{h{^2}}}\)
Para un experto en el campo matemático de las Ecuaciones Diferenciales, esta expresión\ ref {1DSChR} sigue un patrón familiar que facilita la traducción. Si no eres un experto en ecuaciones diferenciales, eso está bien; solo tendrás que soportar esto mientras las cosas se ponen un poco “onduladas a las manos” y prueba Ejercicio\(\PageIndex{2}\) para demostrarte a ti mismo que la siguiente “ondulación de las manos” es verdad. Un experto en ecuaciones diferenciales podría decirte que cuando la segunda derivada de una función es igual a una constante negativa multiplicada por esa misma función, la función se puede escribir en términos de\(sin\) y\(cos\), como se muestra en la Ecuación\ ref {wf1} (esa era la parte ondulada a mano... ver, no tan mal):
\[\psi=A\sin(rx) + B\cos(sx) \label{wf1} \]
\(A, B, r,\)y\(s\) son constantes en la Ecuación\ ref {wf1}. Esta expresión es útil porque está en una forma que podríamos trazar con un programa gráfico (o calculadora). No obstante, para ello debemos conocer las constantes\(A, B, r,\) y\(s\).
¿Qué son\(r\) y\(s\)?
Si sustituimos la expresión\ ref {wf1} en Ecuación\ ref {1DSChR} y resolvemos para r y s, encontramos las expresiones a continuación.
\[r=s=\sqrt{2m_eE}\left(\frac{2\pi}{h}\right) \label{rs} \]
Esto nos muestra que r y s son iguales y constantes; conocemos los valores para\(\pi, h,\) y\(m_e\), y podemos resolver para la constante\(E\).
Mostrar que la Ecuación\ ref {wf1} es verdadera en el caso de que la Ecuación\ ref {Schrx} (\(\frac{\partial{^2}\psi(x)}{\partial{x^2}}=-C\psi \)) sea verdadera. También considere la Ecuación\ ref {rs} (\(r,s\)son constantes y\(r=s\)) y explicar por qué la constante\(r\) debe ser igual\(s\).
Para hacer este problema, también necesitarás conocer las reglas básicas de diferenciación\(\sin\) y\(\cos\) funciones, que se detallan a continuación para mayor comodidad.
Reglas de diferenciación para\(sin\) y\(cos\):
\(\frac{d}{dx}\big(\sin(rx)\big)=r\cos(rx)\), donde r es una constante.
\(\frac{d}{dx}\big(\cos(rx)\big)=-r\sin(rx)\), donde r es una constante.
- Contestar
-
Se puede demostrar que\ ref {wf1} es verdadera sustituyendo\ ref {wf1} de nuevo en la Ecuación\ ref {Schrx}; en otras palabras, tomar la segunda derivada de la función,\(\psi=A\sin(rx) + B\cos(sx)\) para mostrar eso\(\frac{\partial{^2}\psi(x)}{\partial{x^2}}=-C\psi \). \(C, r,\)y\(s\) son constantes arbitrarias, y\(r=s\). El valor real de estas constantes es irrelevante para este problema. Aquí hay una manera de abordar el problema:
(1) Sustituir\(\textcolor{red}{\psi=A\sin(rx) + B\cos(sx)}\) en\(\textcolor{blue}{\frac{\partial{^2}\psi(x)}{\partial{x^2}}=-C\psi} \).
\(\textcolor{blue}{\frac{\partial{^2}}{\partial{x^2}}}\left(\textcolor{red}{A\sin(rx) + B\cos(sx)}\right)= \textcolor{blue}{-C}\textcolor{red}{\psi} \)
(2) Tomar la primera y segunda derivada de\(\textcolor{red}{A\sin(rx) + B\cos(sx)}\).
El resultado de tomar la primera derivada...
\(\textcolor{blue}{\frac{\partial{}}{\partial{x}}}\left(\textcolor{green}{r}\textcolor{red}{A\cos(rx) - \textcolor{green}{s}B\sin(sx)}\right)= \textcolor{blue}{-C}\textcolor{red}{\psi} \)
... y la segunda derivada...
\(\textcolor{green}{-r^2}\textcolor{red}{A\sin(rx)} - \textcolor{green}{s^2}\textcolor{red}{B\cos(sx)} = \textcolor{blue}{-C}\textcolor{red}{\psi}\)
Aquí es donde vemos que la única manera\(\psi=A\sin(rx) + B\cos(sx)\) es si podemos factorizar los valores\(r^2\) y\(s^2\) fuera del lado izquierdo. Tenemos un indicio que\(r=s\) de la discusión anterior y la Ecuación\ ref {rs}. Ahora vemos que esta es una condición necesaria para que la expresión\(\textcolor{green}{-r^2}\textcolor{red}{A\sin(rx)} - \textcolor{green}{s^2}\textcolor{red}{B\cos(sx)} = \textcolor{blue}{-C}\textcolor{red}{\psi}\) sea cierta.
(3) Simplificar
Si\(r=s\), entonces\(r^2=s^2\) y podemos sustituir s por r en la ecuación anterior, como así...
\(\textcolor{green}{-r^2}\textcolor{red}{A\sin(rx)} - \textcolor{green}{r^2}\textcolor{red}{B\cos(sx)} = \textcolor{blue}{-C}\textcolor{red}{\psi}\)
Ahora, podemos factorizar la constante,\(-r^2\) fuera del lado izquierdo de esta expresión,
\(\textcolor{green}{-r^2}\left(\textcolor{red}{A\sin(rx) + B\cos(sx)}\right) = \textcolor{blue}{-C}\textcolor{red}{\psi}\)
Ahora vemos que\(\psi=A\sin(rx) + B\cos(sx)\) cuando\(-C=-r^2\). En otras palabras, hemos demostrado que eso\(\psi=A\sin(rx) + B\cos(sx)\) es cierto.
¿Por qué es esto un ejercicio útil?
Si bien es difícil explicar la derivación de la expresión\(\psi=A\sin(rx) + B\cos(sx)\) sin ecuaciones diferenciales y sólo saber eso\(\frac{\partial{^2}\psi(x)}{\partial{x^2}}=-C\psi \), demostrar que esto es cierto es tan sencillo como resolver este ejercicio. Este ejercicio está aquí para ayudarte a revisar tu cálculo y mostrarte que el “agitar las manos” en el texto anterior no es mágico, sino que viene de matemáticas que has visto en tus cursos de cálculo. ¡Las matemáticas son cruciales para explicar la naturaleza del universo! Come sus verduras y practique sus matemáticas.
*Completa el ejercicio\(\PageIndex{2}\) antes de intentar este.
Derive la expresión para r a continuación (de la Ecuación\ ref {rs}) usando la función de onda 1-D (\ ref {wf1}:\(\psi=A\sin(rx) + B\cos(sx) \)) y la ecuación de Schrödinger 1-D (\ ref {1DSChR}:\(\left(\frac{-h{^2}}{8\pi{^2}m_e}\left(\frac{\partial{^2}\psi(x)}{\partial{x^2}}\right) = E\psi\right)\)).
\(r=\dfrac{2\pi}{h}\sqrt{2m_eE}\)
- Contestar
- Los siguientes pasos podrían llevarse a cabo en una secuencia diferente:
(1) Reorganizar
Vamos a mover todas las constantes al lado derecho de\ ref {1dSchR} para que lleguemos a la expresión que se muestra en parte de la Ecuación\ ref {Schrx}.
\(\dfrac{\partial{^2}\psi(x)}{\partial{x^2}} = \textcolor{green}{\dfrac{-8\pi{^2}m_eE}{h{^2}}}\psi\)
(2) Tomar la segunda derivada de\(\psi\), la cual encontramos en Ejercicio\(\PageIndex{2}\).
\(\dfrac{\partial{^2}\psi(x)}{\partial{x^2}} =\textcolor{green}{-r^2}\left(\textcolor{red}{A\sin(rx) + B\cos(sx)}\right) = \textcolor{green}{\dfrac{-8\pi{^2}m_eE}{h{^2}}}\textcolor{red}{\psi}\)
Y ya que\(\textcolor{red}{\psi=A\sin(rx) + B\cos(sx)}\), podemos simplificar esto dividiendo ambos lados por\(\psi\) (o por\(A\sin(rx) + B\cos(sx) \)).
**recuerda eso\(s=r\). Entonces, podrías haber sustituido\(r\)\(s\) en la expresión anterior, y seguirías en el camino correcto.
\(\textcolor{green}{-r^2}= \textcolor{green}{\dfrac{-8\pi{^2}m_eE}{h{^2}}}\)
(3) Resolver por r (*ya mostramos\(r=s\) en el Ejercicio\(\PageIndex{2}\)).
\(\textcolor{green}{r} = \sqrt{\dfrac{8\pi{^2}m_eE}{h{^2}}} = \dfrac{2\pi}{h}\sqrt{2m_eE}\)
¿Qué son\(A\) y\(B\)?
Podemos encontrar los posibles valores de\(A\) y\(B\) observando los posibles extremos para el valor de\(x\). En nuestro modelo en Figura\(\PageIndex{1}\), podemos ver que x puede tener valores de\(0\rightarrow a\). Los dos extremos, dónde\(x=0\) y\(x=a\), se encuentran en las paredes de la caja. El electrón no puede existir más allá de estos valores porque está atrapado dentro de las paredes, por lo que su función de onda debe ser cero en\(x=0\) y\(x=a\).
El caso donde nos\(x=0\) puede ayudar a encontrar el valor de\(B\). Acabamos de decir que la función de onda debe ser cero donde\(x=0\). Esto significa:
\[\psi_{x=0} = A\sin(rx) + B\cos(sx) = A\sin(0) + B\cos(0) = 0 \nonumber \]
Porque\(A\sin(0)=0\), la expresión puede simplificarse para:
\[\psi_{x=0} = B\cos(0) = B(1) = 0 \nonumber \]
Ahora podemos ver que sólo hay un valor posible para la constante,\(B\), que permitiría que esta expresión sea cierta,\(B=0\). Y como\(B\) es constante entonces siempre será cero a pesar del valor de\(x\). Esto simplifica nuestra función de onda 1-D:
\[\psi=A\sin(rx) \label{wf2} \]
El caso donde nos\(x=a\) puede ayudar a encontrar el valor para\(A\). Dado que la función de onda debe ser cero donde\(x=a\):
\[\psi_{x=a} = A\sin(rx) = A\sin(ra) = 0 \nonumber \]
En este caso,\(A\) no puede ser cero porque si tanto A como B son cero, la función de onda es cero en todos los valores de\(x\), y así nuestra función de onda no existiría dentro de la caja. Entonces, supongamos que A no es cero. Entonces, debe darse el caso que
\[\sin(ra)=0 \nonumber \]
y luego por la forma en que funcionan\(\sin\) las funciones, la cantidad\(ra\) debe ser un valor entero de\(\pi\) if\(\sin(ra)=0\).
\[ra = \pm n\pi \nonumber \]
donde\(n\ = 1, 2, 3...\) cualquier entero distinto de cero. Podemos ignorar los valores negativos aquí ya que tanto los valores positivos como los negativos de\(r\) darán el mismo valor para\(\sin(ra)\). Entonces podemos resolver para r:
\[r=\frac{n\pi}{a} \label{r} \]
y sustituya el valor\(r=\dfrac{n\pi}{a}\) en Ecuación\ ref {wf2} para obtener:
\[\psi = A\sin\left(\frac{n\pi{x}}{a}\right) \label{wf3} \]
Recordemos que el cuadrado de la función de onda (\(\psi^2\)) da la probabilidad de encontrar el electrón en cualquier lugar del espacio. En nuestro modelo, la probabilidad de encontrar la onda de partícula dentro de la caja es la unidad (es 1). Matemáticamente, este es el requisito normalizador (expresado como\(\int \psi_A \psi_A^* d\tau=1\)), que se puede resolver para encontrar el valor de A.
\[A = \sqrt{\frac{2}{a}} \nonumber \]
Ahora, podemos sustituir el valor de\(A\) en expresión\ ref {wf3}, y tenemos una función de onda que se puede visualizar usando cualquier programa/calculadora gráfica!
\[\psi=\sqrt{\frac{2}{a}}\left(\sin\left(\frac{n\pi{x}}{a}\right)\right) \label{wf4} \]
¿Cuál es la energía (E) de una partícula en la caja?
Entonces, ahora puedes ver cómo se puede resolver una función de onda 1-D. Pero, ¿cómo encontramos la E del electrón a partir de esto? Bueno, para no distraerte antes, nos saltamos una forma muy sencilla de hacer esto. La E cae justo fuera de las ecuaciones que acabas de ver. Podemos establecer las dos expresiones que encontramos anteriormente para la constante\(r\), (ecuaciones\ ref {rs} y\ ref {r}) iguales entre sí y luego resolver para E:
\[r=\dfrac{n\pi}{a}=\sqrt{2mE}\left(\dfrac{2\pi}{h}\right) \nonumber \]
\[E=\frac{n^2h^2}{8ma^2} \label{E} \]
La expresión\ ref {E} se puede utilizar para calcular la energía de una partícula en una caja unidimensional de longitud\(a\), dado su nivel de energía entera,\(n\). Aquí podemos ver que la energía se cuantifica porque\(n\) es un entero (\(n=1,2,3...\)). En otras palabras,\(n\) es un número cuántico.
Dar sentido a la partícula en una caja: trazando el 1-D\(\psi\) y\(\psi^2\).
No importa si se trata de una ecuación de onda unidimensional o tridimensional, la función de onda en sí (\(\psi\)) describe las propiedades de onda de la partícula. Esto\(\psi\) no tiene un significado físico real, por lo que es difícil imaginar cómo “se ve” aparte de simplemente trazar su función. Sin embargo, la probabilidad de encontrar la onda de partícula en cualquier posición específica a lo largo del eje x entre\(x=0\) y\(x=a\) es más significativa físicamente. La probabilidad de encontrar la partícula es proporcional al cuadrado de la función de onda, que se representa por cualquiera\(\psi^2\) o, a veces,\(\psi\psi^*\). Las gráficas de las funciones para\(\psi\) y\(\psi^2\) para los tres primeros valores posibles de se\(n\) muestran a continuación en la Figura\(\PageIndex{2}\). Podrías crear gráficas similares a estas simplemente trazando la función que se muestra en la ecuación\ ref {wf4}. Para trazar, solo necesitas asignar un valor de\(n\), y es conveniente asignar la longitud de la caja como\(a=1\). La parcela generada tendría la relación general de\(\frac{x}{a}\) sobre el eje x, y por lo tanto sería relevante para cualquier caja de longitud.
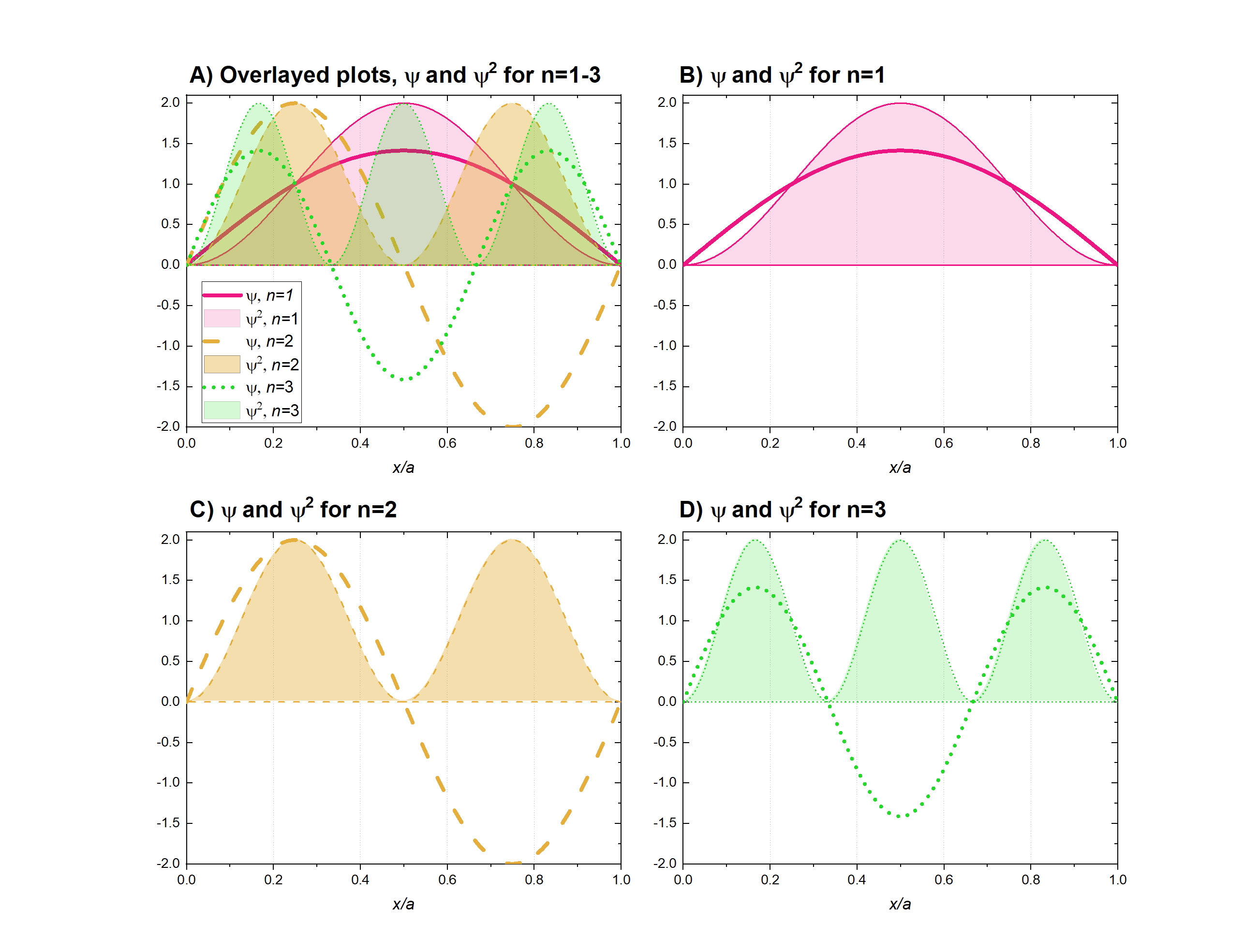
Las gráficas anteriores representan “soluciones” a la función de onda. Por ejemplo, la solución\(n=1\) da la gráfica mostrada en la Figura\(\PageIndex{2}\) B. La solución de\(n=2\) se grafica en la Figura\(\PageIndex{2}\) C, y así sucesivamente. Estos valores para\(n\) son algunas de las posibles soluciones a lo 1-dimensional\(\psi\), y dan descripciones del comportamiento de onda y probabilidad de encontrar una partícula en el espacio 1-dimensional.
¿Cómo se aplica esto a los átomos?
La partícula unidimensional en una caja no representa una situación real; sino que es un modelo sencillo que podemos utilizar para entender un sistema más complejo, como un electrón que orbita el núcleo en tres dimensiones. Es útil reconocer aquí las analogías que podrían representar algo familiar en una situación real.
\(x=0\)es análogo al núcleo en un átomo. Aquí en la partícula en un modelo de caja,\(\psi=0\) y hay cero probabilidad de encontrar un electrón. Cuando éste se extiende a un átomo, esta posición es análoga al núcleo (en el origen de un sistema de coordenadas donde\(x=y=z=0\). Un tridimensional también\(\psi\) es cero en el núcleo y el electrón no puede existir allí; también,\(\psi\) se acerca a cero ya que se acerca a esta posición tanto en la partícula en un modelo de caja como en un caso más realista de un electrón en un átomo.
\(x=a\)es análogo a una superficie límite alejada del núcleo. En la partícula en un modelo de caja, el 1-dimensional\(\psi\) es cero en\(x=a\). Esto es análogo a que un electrón\(\psi\) se acerca a cero a medida que se aleja del núcleo. Habrá una descripción más profunda de la superficie límite en la siguiente sección (2.2.2). Ya se sabe esto como la superficie más externa de un orbital electrónico. Una diferencia menor pero notable entre la partícula unidimensional en una caja y el caso de un átomo real es que la\(\psi\) en tres dimensiones se acerca pero nunca alcanza del todo cero a medida que aumenta la distancia desde el núcleo, mientras que\(\psi=0\) para\(x=a\) en el caso más simple de una partícula unidimensional en una caja.
Un cambio en el signo del\(\psi\) (y donde ambos\(psi=0\) y\(\psi^2=0\)) es un nodo. Tanto en la partícula unidimensional en un modelo de caja como en el caso tridimensional más realista, se encuentra un nodo donde se muestran los\(\psi\) cambios. En este punto,\(\psi=\psi^2=0\); en otras palabras hay cero probabilidad de encontrar la partícula o electrón en estos puntos. Es fácil detectar estos puntos en las gráficas anteriores porque la función de onda cruza el eje x y el\(\psi^2\) cumple con cero.
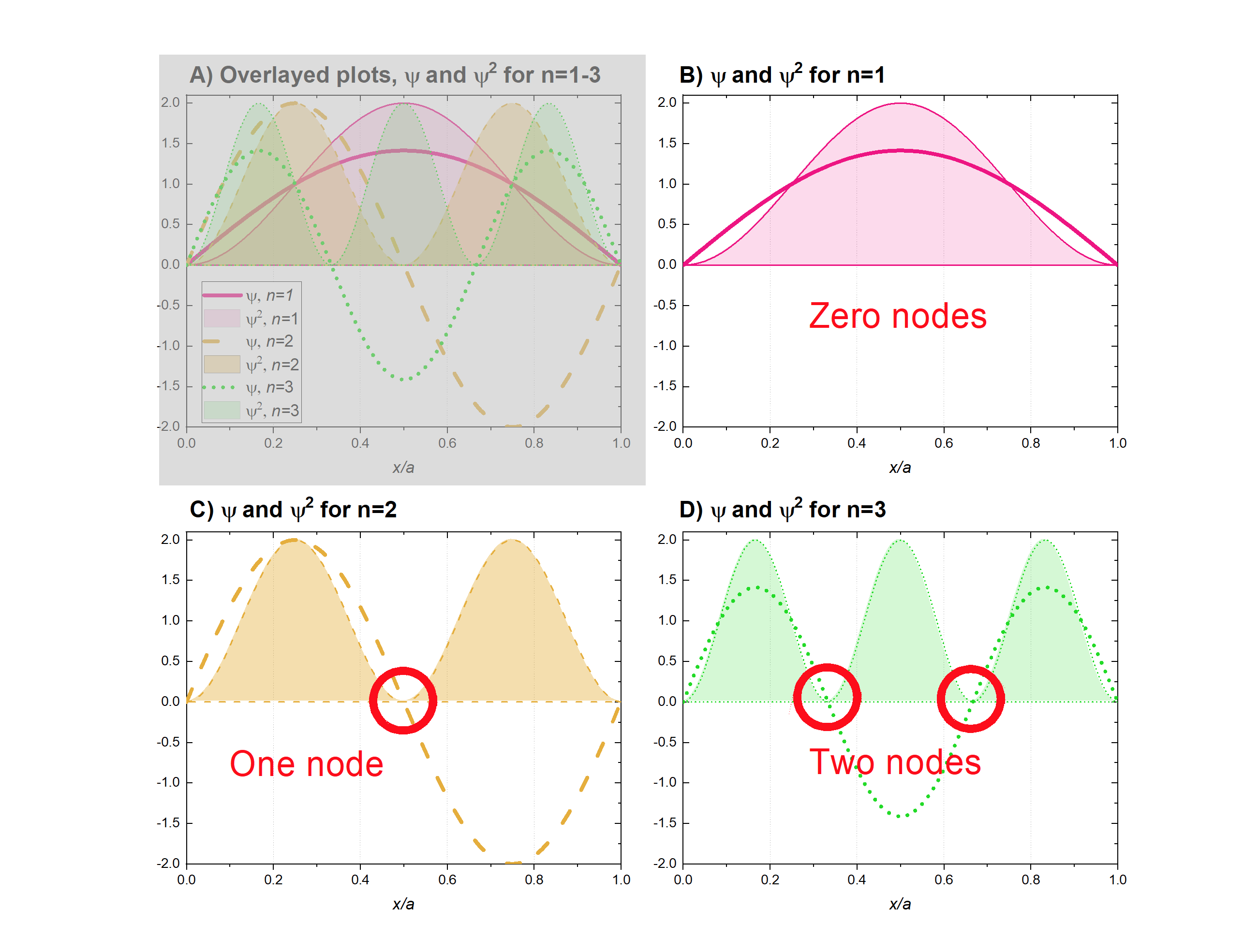
Identificar los puntos en las parcelas B, C y D en la Figura\(\PageIndex{2}\) que son nodos. ¿Para cuántos nodos hay\(n=1, n=2,\) y\(n=3\)?
- Contestar
-
Los nodos están anotados con círculos rojos en la siguiente figura. El panel B (\(n=1\)) tiene cero nodos. Hay dos puntos donde\(\psi=0\) en el caso de\(n=1\), pero estos puntos están en las paredes de la caja y no son nodos. Las paredes de la caja son análogas al núcleo y la superficie límite de un orbital electrónico. El panel C (\(n=2\)) tiene un nodo donde el\(\psi\) cruza cero. El panel D (\(n=3\)) muestra dos nodos.
Utilice un programa de gráficos para trazar el 1-dimensional\(\psi\) y\(\psi^2\) para\(n=1,2,3,4\). ¿Para cuántos nodos hay\(n=4\)? ¿Esto se espera? Predecir cuántos nodos debemos esperar\(n=5\).
Puedes usar cualquier programa de plotting para hacer esto, y si no estás familiarizado con alguno, prueba este: Desmos
- Contestar
-
Puedes usar cualquier programa de plotting para hacer esto. Esta es la función que debes trazar (es Ecuación\ ref {wf4}):
\(\psi=\sqrt{\frac{2}{a}}\left(\sin\left(\frac{n\pi{x}}{a}\right)\right)\)
Para n=1: Asignar un valor de\(n=1\), como se indica en el problema. En el texto anterior, también señala que es conveniente asignar un valor de\(a=1\). La asignación de estos valores da como resultado la siguiente función:
\(\psi=\sqrt{\frac{2}{1}}\left(\sin\left(\frac{1\pi{x}}{1}\right)\right)\)y simplificar conduce a\(\psi=\sqrt{2}\left(\sin\left(\pi{x}\right)\right)\)
Para n=2,3,4 repetirías el proceso anterior. Obtendrá las siguientes funciones:
Para n=2:\(\psi=\sqrt{2}\left(\sin\left(2\pi{x}\right)\right)\)
Para n=3:\(\psi=\sqrt{2}\left(\sin\left(3\pi{x}\right)\right)\)
Para n=4:\(\psi=\sqrt{2}\left(\sin\left(4\pi{x}\right)\right)\)
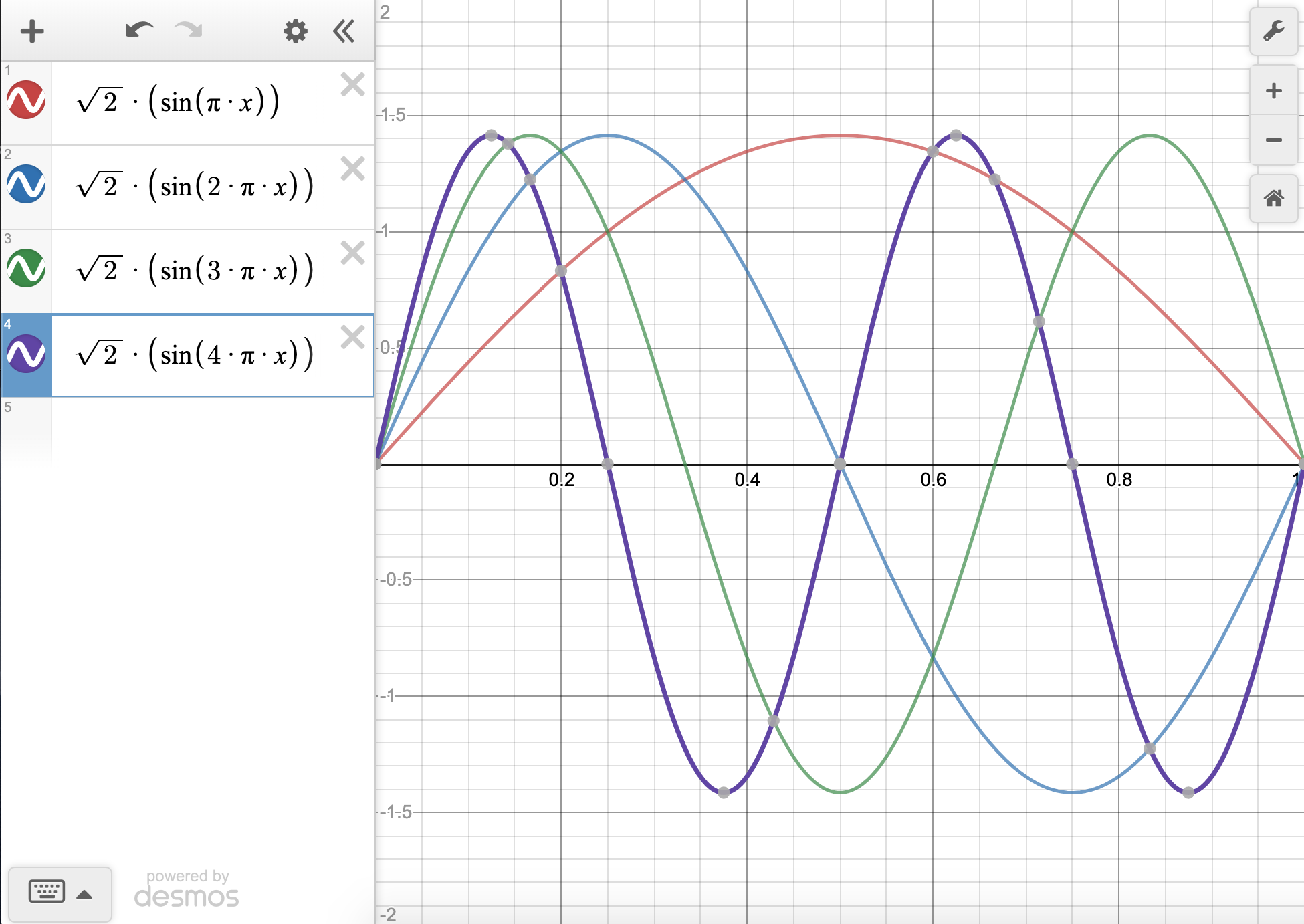
En un programa como Desmos, es necesario ingresar la función correctamente. Es útil conocer el código de al menos un programa de gráficos. Para Desmos, y la mayoría de los demás, puedes encontrar ayuda en línea. Por ejemplo, la entrada correcta para Desmos para el caso n=4 es sqrt (2) * (sin (4*pi*x)). Pero, hay que teclearlo porque copiar/pegar no funciona. También querrás mostrar tu gráfica solo de\(x=0\) a\(x=1\) presionando el botón de configuración (una pequeña llave en la esquina superior derecha) y cambiando la escala x. Adelante y cambia la escala y también, a\(y=-2\) a\(y=2\). Si haces esto, deberías conseguir algo que se vea así:
Para graficar el cuadrado de cada funcion de onda, solo cuadrarias las funciones que acabamos de trazar:
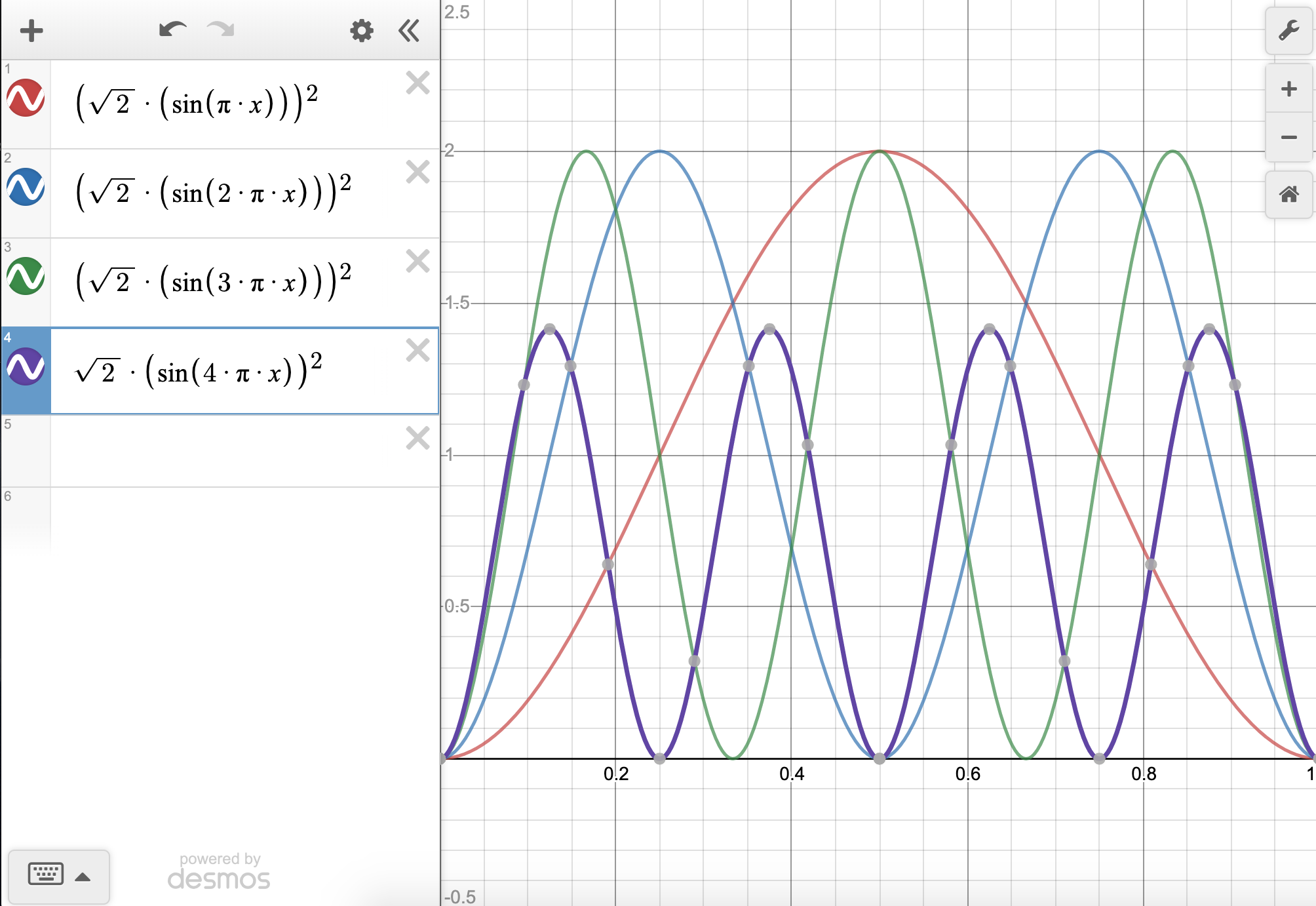
Tanto en el caso de\(\psi\) como\(\psi^2\), la\(n=4\) función muestra tres nodos (ver la línea púrpura en negrilla, donde los nodos son diminutas manchas grises en el eje). Esto sigue un patrón que podrías haber notado con los casos de\(n=1,2,\) y\(3\) donde está el número de nodos\(n-1\) (nodes =\(n-1\)). Deberíamos esperar tres nodos para\(n=4\) basado en este patrón, y cuatro nodos para\(n=5\).
En la siguiente sección, extenderemos estas ideas cualitativamente a tres dimensiones. Si bien solo hay un número cuántico en una dimensión, hay tres números cuánticos en tres dimensiones que (cuando se combinan) dan descripciones discretas de un electrón en el espacio tridimensional (más un cuarto número cuántico que explica otras propiedades del electrón).


