2.2.2: Números cuánticos y funciones de onda atómica
- Page ID
- 81222
La partícula unidimensional en un modelo de caja de la sección anterior nos muestra cómo funciona una función de onda en una dimensión (la dimensión x). En una dimensión, la función de onda requiere sólo un número cuántico,\(n\). Una explicación completa de la función de onda tridimensional para un electrón está fuera del alcance de este curso. En cambio, nos enfocaremos en obtener una comprensión conceptual extendiendo el conocimiento de la función de onda unidimensional a un espacio tridimensional.
Números cuánticos
Extender la función de onda a tres dimensiones requiere un total de tres números cuánticos. Además de\(n\), que vimos en el caso unidimensional, también necesitamos\( l\) y\(m_l\) expresar la función ondulada en tres dimensiones. Una solución completa a la ecuación de Schrödinger, tanto la función de onda tridimensional como la energía, incluye un conjunto de tres números cuánticos (\(n, l, m_l\)). La función de onda describe lo que conocemos como orbital atómico; define la región en el espacio donde se encuentra el electrón. Adicionalmente, hay un cuarto número cuántico,\(m_s\). El número\(m_s\) cuántico da cuenta de la interacción observada de electrones con un campo magnético aplicado; es un postulado adicional que no forma parte de la función de onda. Estos cuatro números cuánticos se describen a continuación.
El número cuántico,\(n\): Este es el número cuántico principal. Este número representa el caparazón, incluyendo tanto la energía general del electrón en esa concha como el tamaño de esa concha. Un valor permitido para\(n\) es cualquier entero positivo distinto de cero (se permiten 1, 2, 3, 4,... etc, pero 4.1 no está permitido).
El número cuántico,\(l\): Este es el número cuántico de momento angular que corresponde a la subcapa y su forma. Representa la dependencia angular de la subcapa, o la “forma” de los orbitales dentro de una subcapa. Los valores permitidos de\(l\) dependen de\(n\). Los valores permitidos de\(l\) para un electrón en shell\(n\) son valores enteros entre\(0\) a\(n-1\), o\(l = 0\rightarrow n-1\). Estos valores corresponden a la forma orbital donde\(l=0\) es un s-orbital,\(l=1\) es un p-orbital,\(l=2\) es un d-orbital, y\(l=3\) es un f-orbital.
El número cuántico\(m_l\): Este es el número cuántico magnético. Sus posibles valores dan el número de orbitales dentro de una subcapa y su valor específico da la orientación orbital en el espacio. Los valores permitidos de\(m_l\) dependen del valor de\(l\). Se permite\(m_l\) que el valor de sea cualquier entero positivo o negativo entre\(+l\) y\(-l\). En otros términos,\(m_l=+l \rightarrow -l\). Por ejemplo, si el electrón está en un orbital 3-p, entonces\(n=3, l=1\), y los posibles valores de\(m_l\) son\(-1, 0,\) y\(+1\). Ya que hay tres valores posibles de\(m_l\) hay tres orbitales en el\(p\) subshell. El\(m_l\) valor específico define en cuál de los tres posibles orbitales p (\(p_x, p_y,\)o\(p_z\)) existe el electrón. En el caso del\(s\) subshell, sólo hay un valor,\(m_l=0\) porque\(l=0\). El único valor corresponde al hecho de que sólo hay un\(s\) orbital en cualquier caparazón.
El número cuántico\(m_s\): Este número cuántico da cuenta del “giro” del electrón. En resumen, los electrones interactúan con los campos magnéticos de una manera que es similar a cómo un pequeño imán de barra interactuaría con un campo magnético. Los valores permitidos para\(m_s\) son\(+\frac{1}{2}\) y\(-\frac{1}{2}\).
| SÍMBOLO | NOMBRE | VALORES | SIGNIFICADO |
|---|---|---|---|
| \(n\) | principal | \(1,2,3...\)(cualquier entero) | nivel de energía, shell |
| \(l\) | momento angular | \(0 \rightarrow n-1\) |
subshell,\(0=s, 1=p, 2=d, 3=f...\) esta es la dependencia angular de lo orbital, forma de la |
| \(m_l\) | magnético | \(+l \rightarrow -l\) | orientación del momento angular en el espacio, orbital |
| \(m_s\) | giro | \(+\frac{1}{2}, -\frac{1}{2}\) | la propiedad imaginaria que llamamos “spin”, arriba o abajo |
Funciones de onda de 1 electrones (orbitales atómicos)
A continuación se muestra una representación simplificada de la función de onda tridimensional. Esta representación divide la función de onda en dos partes: la contribución radial (\(\textcolor{blue}{R_{n,l}(r)}\)) y la contribución angular (\(\textcolor{red}{Y_{l,m_l}(\theta,\phi)}\)).
\[\psi_{(n,l,m_l)}= \textcolor{blue}{R_{n,l}(r)} \times \textcolor{red}{Y_{l,m_l}(\theta,\phi)} \label{WF1} \]
Energías Permitidas
A partir de la función de onda, podemos encontrar las energías permitidas de un electrón en un átomo. No te hemos dado la forma más compleja de la función de onda donde necesitarías derivar\ ref {E} de\ ref {WF1} porque está fuera del alcance de este curso. En cambio, consideremos el proceso que utilizamos para derivar la energía de una partícula en una caja unidimensional en la sección anterior. Un proceso similar se puede utilizar para encontrar la energía de un electrón en tres dimensiones, que se muestra en\ ref {E}.
\[E_n = -\frac{hcRZ^2}{n^2}=-(13.607\thinspace eV) \left(\frac{Z}{n}\right)^2 \label{E} \],
donde\(n\) está el número cuántico principal,\(h\) es la constante de Planck,\(c\) es la velocidad de la luz,\(R\) es la constante de Rydberg, y\(Z\) es la carga del núcleo. Es útil saber que el valor de\(hcR = 13.6 eV\). Este es también el valor de la energía de ionización de un electrón en un átomo de hidrógeno. Esta ecuación sólo funciona para los átomos hidrogénicos (átomos o iones que son “como” el hidrógeno en que tienen un solo electrón).
La energía que se necesita para expulsar un electrón de estado fundamental de un átomo de hidrógeno (su energía de ionización, IE) se mide para ser aproximadamente 13.6 eV, mientras que la energía IE de un ion He + es cuatro veces mayor a 54.4 eV. Estos valores se pueden predecir usando tanto la Ecuación\ ref {E} como la ecuación de Rydberg.
- Usando la Ecuación\ ref {E} para las energías permitidas de electrones en un átomo de hidrógeno, derivar la energía del electrón del estado fundamental en H. Luego repita este proceso para un ion He +. ¿Qué indican los valores sobre la atracción relativa entre un electrón y los núcleos de estos dos átomos hidrogénicos?
- Mostrar que el IE del electrón 1s de H también puede ser predicho por la fórmula de Rydberg (ecuación 2.1.2.2).
- Respuesta (a)
-
Usa la Ecuación\ ref {E}. Para un átomo de hidrógeno con un protón,\(Z=1\), y el nivel de energía del estado fundamental es el nivel de energía más bajo,\(n=1\). Por lo tanto, la energía de un electrón en el estado fundamental de un átomo de H es:
\(E_n = -\frac{hcRZ^2}{n^2} = -13.607\thinspace eV(\frac{1}{1})^2 = -13.607 \thinspace eV \), o aproximadamente\(-13.6 \thinspace eV\). Así, el IE (energía necesaria para eliminar ese electrón) es +13.6 eV.
Podemos usar el mismo proceso para encontrar la energía del estado fundamental de un electrón en He +. Esta vez,\(Z=2\) porque el helio tiene dos protones en su núcleo, y como antes, el estado fundamental lo es\(n=1\).
\(E_n = -\frac{hcRZ^2}{n^2} = -13.607\thinspace eV(\frac{2}{1})^2 = -54.428 eV \), o aproximadamente\(-54.4 \thinspace eV\). Así, el IE es +54.4 eV.
Estas energías de estado fundamental son las mismas que la energía requerida para eliminar el electrón del estado fundamental de H y He +. En otras palabras, estos son los valores de IE del estado fundamental pronosticados para un electrón en H y He +. Los IE medidos para estas dos especies son de hecho 13.6 eV y 54.4 eV, respectivamente.
El ion He + tiene un valor más negativo para su energía de estado fundamental con una magnitud cuatro veces mayor que la del electrón H del estado fundamental. Esto significa que el electrón He + es atraído más fuertemente por el núcleo (+2) que el electrón H es atraído por el núcleo (+1), y se requiere más energía para expulsar el electrón He + que el electrón H. Se necesita más energía para eliminar el electrón de He + que de H. Esto tiene sentido a la luz de la ley de Coulomb: La fuerza atractiva entre el núcleo H (+1) y un electrón (-1) sería más débil que la de un núcleo de He (+2) y un electrón (-1) porque la carga positiva del núcleo He tiene un mayor magnitud.
- Respuesta (b)
-
La ecuación de Rydberg es:\( \dfrac{1}{\lambda }= E (cm^{-1})= R_H\; \left ( \dfrac{1}{n_l^{2}}-\dfrac{1}{n_h^{2}} \right )\) donde\(n_l\) y\(n_h\) son enteros positivos,\(n_h > n_l\), y la constante de Rydberg (\(R_H\)), tiene un valor de 1.09737 × 10 7 m −1. Debemos establecer\(n_l=1\) para representar el estado fundamental inicial, y\(n_h=\infty\) para representar la eliminación del electrón del átomo.
Paso 1.
Calcular Energía (en m -1) usando la ecuación de Rydberg:
\(E = R_H\left( \dfrac{1}{n_l^{2}}-\dfrac{1}{n_h^{2}} \right) = 1.09737\times10^7 m^{-1} \left( \dfrac{1}{1^{2}}-\dfrac{1}{\infty^{2}} \right ) = 1.09737\times10^7 m^{-1} \left( 1-0 \right ) = 1.09737 \times 10^7 m^{-1}\)
En definitiva, queremos un valor de energía en unidades de eV para poder compararlo con las respuestas en la parte (a), pero nuestro valor aquí está en unidades de metros inversos (m -1). Una búsqueda rápida en Internet puede indicarle la conversión entre centímetros inversos (cm -1) y eV es\(1 eV = 8065.6 cm^{-1}\).
Paso 2.
Convertir de m -1 a cm -1 a eV para que podamos comparar con la respuesta en la parte (a):
\(1.09737\times 10^7 \frac{1}{m} \times \dfrac{1m}{100cm} \times \dfrac{1eV}{8065.6 \frac{1}{cm}} = 13.6056 eV,\)o aproximadamente 13.6 eV.
¿Cuáles de los siguientes son átomos hidrogénicos? H, H +, H -, Él, Él 2 +, Él +, Él -, Li, Li 3 +, Li 2 +, Li +, Li -.
- Contestar
-
Los átomos hidrogénicos son átomos o iones que contienen solo un electrón. H, He + y Li 2 + son átomos/iones hidrogénicos que contienen solo un electrón.
Contribuciones radiales y angulares a la función de onda:
Contribución radial,\(\textcolor{blue}{R_{n,l}(r)}\)
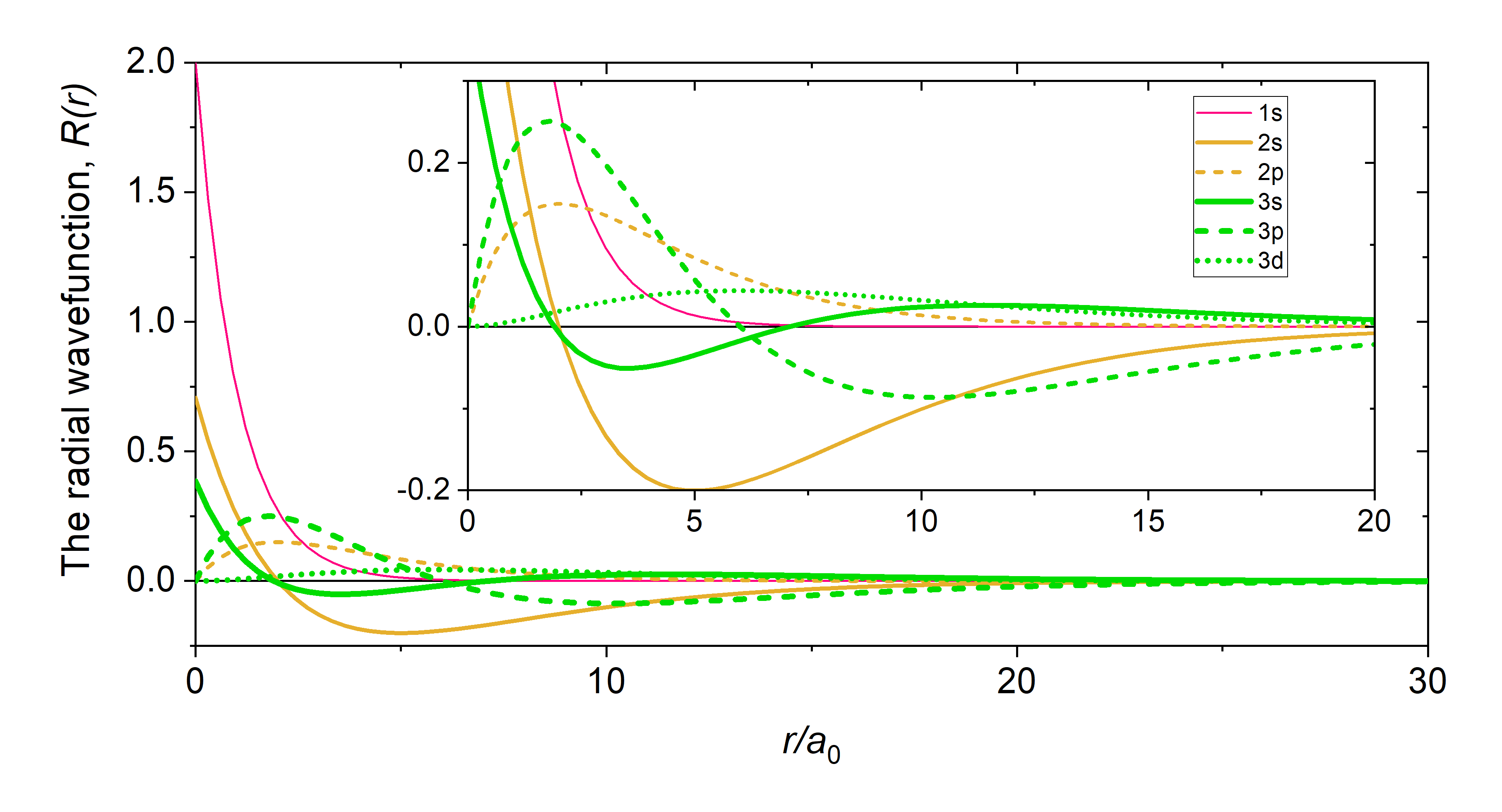
La parte radial de la función ondulada,\(\textcolor{blue}{R_{n,l}(r)}\) da la variación radial de\(\psi\). En otras palabras,\(\textcolor{blue}{R_{n,l}(r)}\) define cómo la función de onda depende de la distancia del electrón desde el núcleo (el radio). Las\(\textcolor{blue}{R_{n,l}(r)}\) partes de la función de onda para un átomo hidrogénico se listan en la Tabla\(\PageIndex{2}\), y se representan gráficamente en la Figura\(\PageIndex{1}\). Observe que el\(R_{n,l}(r)\) de todos los orbitales s (líneas continuas) alcanza un máximo en\(r=0\). Esto es único para los orbitales s”\(R_{n,l}(r)\). Los\(R_{n,l}(r)\) orbitales p- y d orbitales se aproximan a cero a medida que r se acerca a cero. Esto tiene consecuencias importantes por lo cerca que un electrón en estos orbitales puede acercarse al núcleo.
| Orbital | \(n\) | \(l\) | \(\textcolor{blue}{R_{n,l}(r)}\) |
|---|---|---|---|
| 1s | \ (n\)” style="vertical-align:middle; "> 1 | \ (l\)” style="vertical-align:middle; "> 0 | \ (\ textcolor {azul} {R_ {n, l} (r)}\) ">\(2\left[\frac{Z}{a_0}\right]^{3/2}e^{-Zr/a_0}\) |
| 2s | \ (n\)” style="vertical-align:middle; "> 2 | \ (l\)” style="vertical-align:middle; "> 0 | \ (\ textcolor {azul} {R_ {n, l} (r)}\) ">\(2\left[\frac{Z}{2a_0}\right]^{3/2}\left(2-\frac{Zr}{a_0}\right)e^{-Zr/2a_0}\) |
| 2p | \ (n\)” style="vertical-align:middle; "> 2 | \ (l\)” style="vertical-align:middle; "> 1 | \ (\ textcolor {azul} {R_ {n, l} (r)}\) ">\(\frac{1}{\sqrt{3}}\left[\frac{Z}{3a_0}\right]^{3/2}\left(\frac{Zr}{a_0}\right)e^{-Zr/2a_0}\) |
| 3s | \ (n\)” style="vertical-align:middle; "> 3 | \ (l\)” style="vertical-align:middle; "> 0 | \ (\ textcolor {azul} {R_ {n, l} (r)}\) ">\(\frac{2}{27}\left[\frac{Z}{3a_0}\right]^{3/2}\left(27-18\frac{Zr}{a_0}-2(\frac{Zr}{a_0})^2\right)e^{-Zr/3a_0}\) |
| 3p | \ (n\)” style="vertical-align:middle; "> 3 | \ (l\)” style="vertical-align:middle; "> 1 | \ (\ textcolor {azul} {R_ {n, l} (r)}\) ">\(\frac{1}{81\sqrt{3}}\left[\frac{2Z}{a_0}\right]^{3/2}\left(6-\frac{Zr}{a_0}\right)(\frac{Zr}{a_0})e^{-Zr/3a_0}\) |
| 3d | \ (n\)” style="vertical-align:middle; "> 3 | \ (l\)” style="vertical-align:middle; "> 2 | \ (\ textcolor {azul} {R_ {n, l} (r)}\) ">\(\frac{1}{81\sqrt{15}}\left[\frac{2Z}{a_0}\right]^{3/2}\left(\frac{Zr}{a_0}\right)^2e^{-Zr/3a_0}\) |
Función de probabilidad radial,\(\textcolor{black}{4 \pi r^2}\textcolor{blue}{(R_{n,l}(r))^2}\)
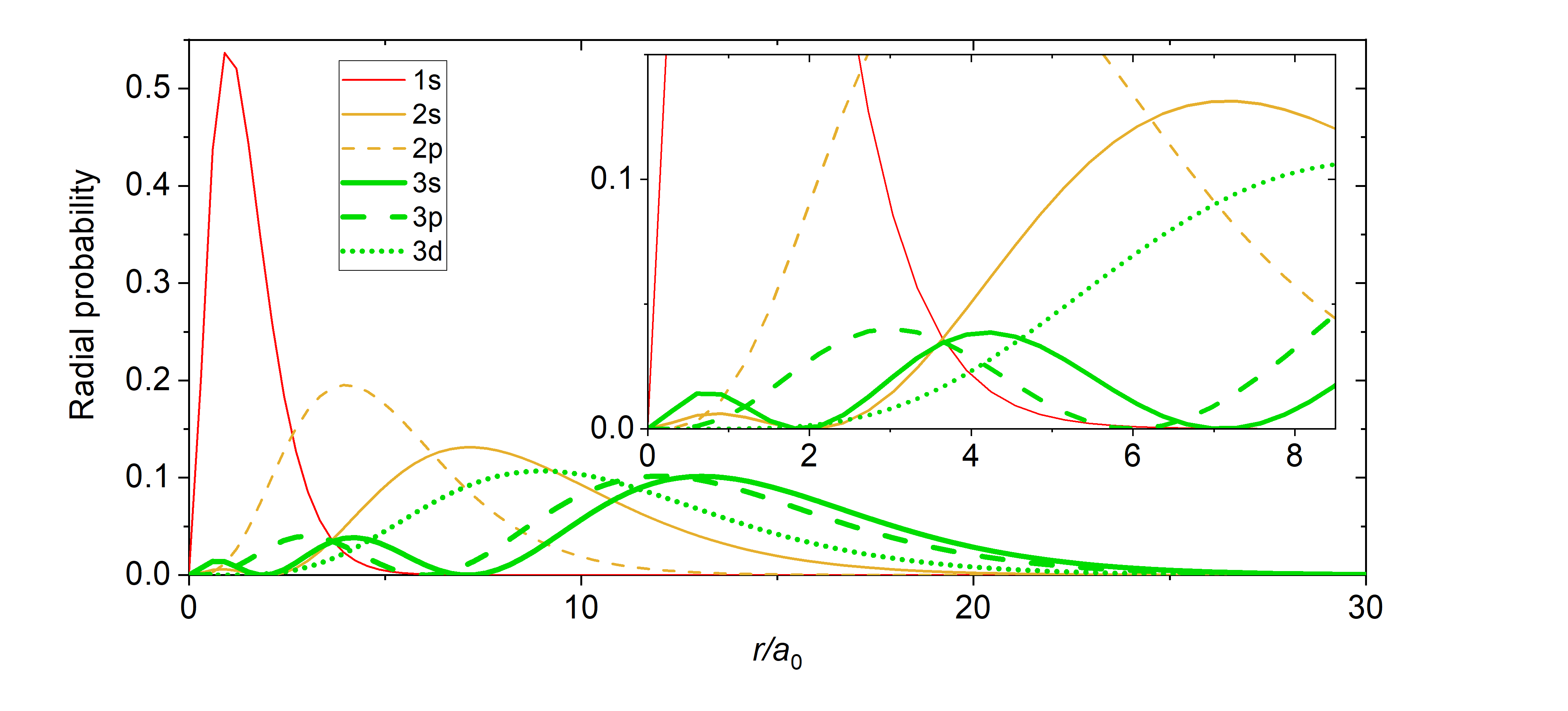
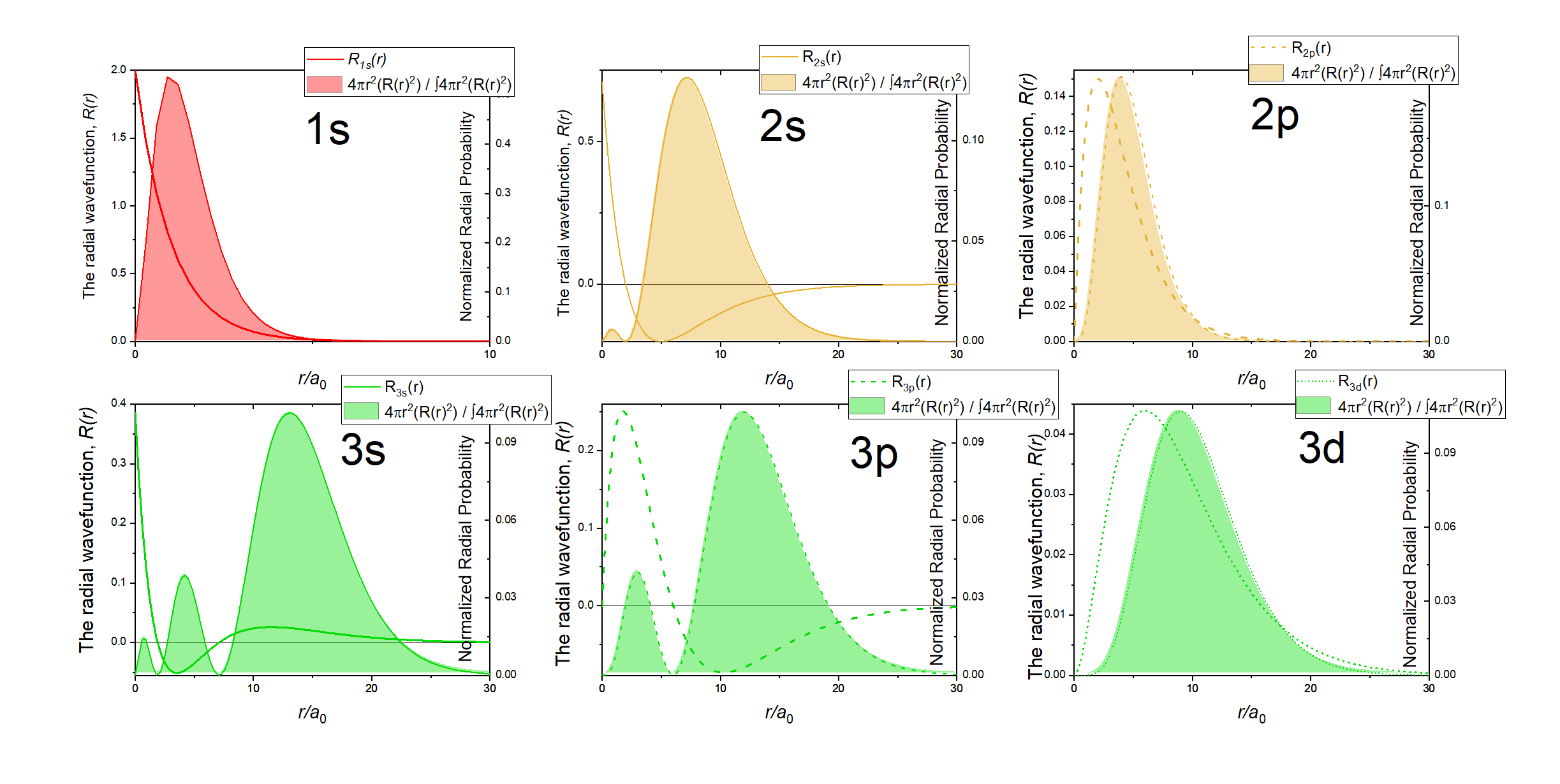
Al igual que en el modelo de partícula en caja, el cuadrado de la función de onda es proporcional a la probabilidad de encontrar una partícula (electrón) en algún punto del espacio. El cuadrado de la parte radial de la función de onda se llama función de distribución radial \(4 \pi r^2\textcolor{blue}{(R_{n,l}(r))^2}\), y describe la probabilidad de ubicar el electrón a cierta\(r\) distancia del núcleo. Cuando normalizamos las funciones de probabilidad dividiendo la función por su integral en todo el espacio, obtenemos las gráficas que se muestran en la Figura\(\PageIndex{2}\). Las funciones de probabilidad normalizadas se comparan con la parte radial original de las funciones de onda en la Figura\(\PageIndex{3}\). La distancia más probable para encontrar un electrón se muestra por el valor máximo de la función. Para un electrón en la órbita 1s de H, la distancia más probable desde el núcleo ocurre en\(r=1a_0\). Este es el Radio de Bohr, y tiene un valor de\(a_0 = 52.9 pm = 0.529 Å\). Es conveniente trazar las funciones de los orbitales atómicos de hidrógeno en relación con el tamaño de su orbital más pequeño, el orbital 1s; esta es la razón por la que trazamos\(R_{n,l}(r)\) y\(4 \pi r^2(R_{n,l}(r))^2\) relativo a\(\frac{r}{a_0}\).
Nodos radiales
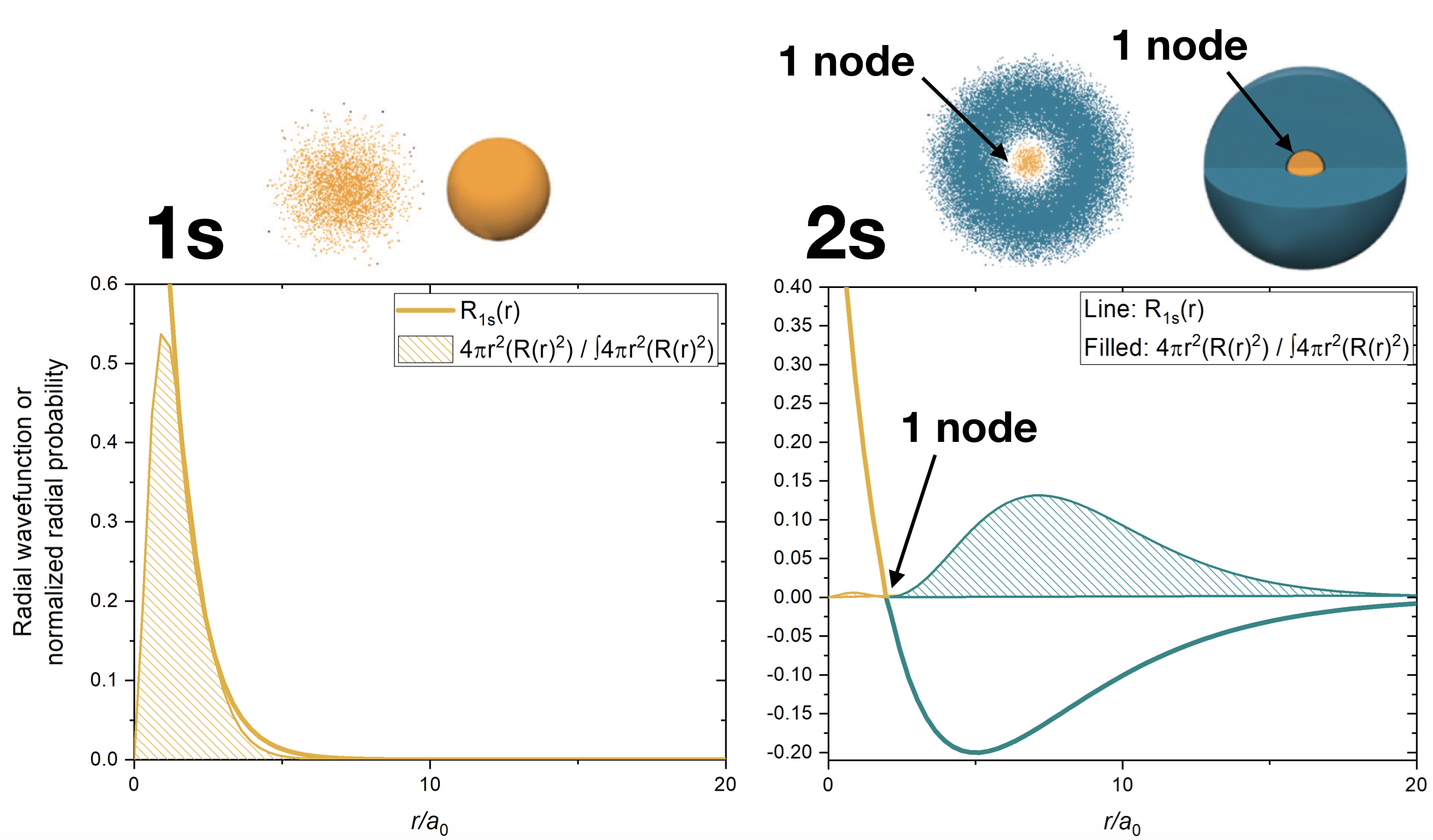
A partir de la discusión de la partícula unidimensional en una caja, aprendimos que los nodos existen donde\(\psi=0\). En el caso de la función de onda tridimensional, existen dos tipos diferentes de nodos: nodos radiales y nodos angulares. Los nodos radiales ocurren donde la parte radial de la función de onda es cero (\(R(x)=0\)). Estos son fáciles de encontrar trazando la parte radial de la función de onda y encontrando dónde la parte radial de la función de onda (y la función de probabilidad radial) es cero (dónde\(\textcolor{blue}{R_{n,l}(r)}=0\)) y dónde\(4 \pi r^2\textcolor{blue}{(R_{n,l}(r))^2}=0\). Estos nodos son de forma esférica y dependen del nivel de energía y la subcapa (los valores de\(n\) y\(l\)). El número de nodos radiales es\(n-l-1\). Un ejemplo de un nodo radial es el nodo único que ocurre en el\(2s\) orbital (\(2-0-1=1\)nodo). En contraste, el orbital 1s tiene cero nodos radiales (\(1-0-1=0\)nodos). Donde hay un nodo, hay cero probabilidad de encontrar un electrón.
Superficies de contorno
Un nodo verdadero ocurre donde la probabilidad de encontrar un electrón es cero. Los nodos ocurren donde\(\psi=\psi^2=0\). Lejos del núcleo, la probabilidad de encontrar el electrón se acerca rápidamente a cero, pero nunca es exactamente cero. Lo que esto significa es que es bastante improbable encontrar el electrón a distancias lejanas del núcleo, pero no es imposible. La rápida caída de probabilidad crea una superficie límite en lugar de un nodo. La superficie límite representa el área alrededor del núcleo donde existe el electrón la mayor parte del tiempo.
¿Cuántos nodos radiales hay en los orbitales s, p, d y f en los primeros cuatro proyectiles? \(n=1,2,3,4\)?
- Contestar
-
Puede abordar esta respuesta utilizando la relación matemática entre el número de nodos radiales y los valores de\(n\) y\(l\): número de nodos radiales es\(n-1-l\). También se podría notar el patrón de que el primer orbital de cualquier tipo (1s, 2p, 3d...) tiene cero nodos radiales, el segundo orbital de un tipo (2s, 3p, 4d...) tiene un nodo radial, el tercer orbital de un tipo tiene dos nodos radiales (3s, 4p, 5d...)... etc.
A continuación se muestra una lista completa de todos los orbitales en los primeros cuatro proyectiles y su número de nodos radiales. Es una buena idea probarse a sí mismo que los números que se dan a continuación son consistentes con las tramas de las funciones de onda de los orbitales para esos orbitales en los tres primeros proyectiles:
orbitales s:
1s:\(n-1-l = 1-1-0 = 0\), cero nodos radiales
2s:\(n-1-l = 2-1-0 = 1\), un nodo radial
3s:\(n-1-l = 3-1-0 = 2\), dos nodos radiales
4s:\(n-1-l = 4-1-0 = 3\), tres nodos radiales
orbitales p
2p:\(n-1-l = 2-1-1 = 0\), cero nodos radiales
3p:\(n-1-l = 3-1-1 = 1\), un nodo radial
4p:\(n-1-l = 4-1-1 = 2\), dos nodos radiales
orbitales d
3d:\(n-1-l = 3-1-2 = 0\), cero nodos radiales
4d:\(n-1-l = 4-1-2 = 1\), un nodo radial
f-orbital
4f:\(n-1-l = 4-1-3 = 0\), cero nodos radiales
Dibuja una trama aproximada de lo siguiente:
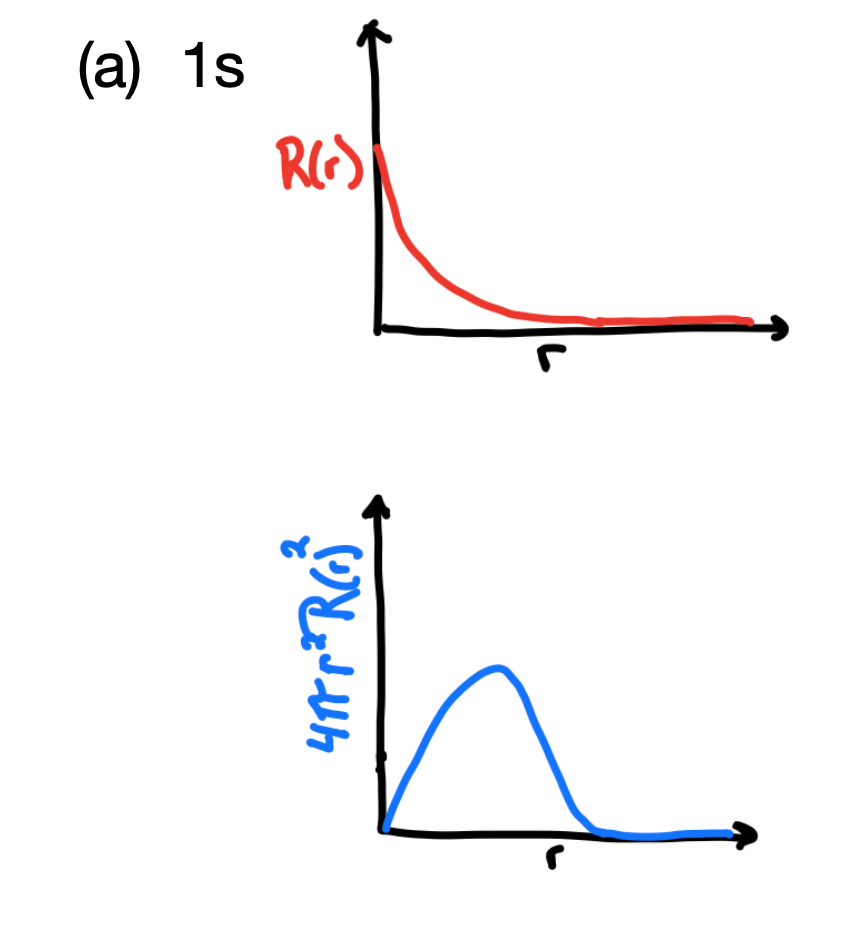
- La función de onda radial,\(R_{n,l}(r)\) y la función de densidad de probabilidad\(4 \pi r^2(R_{n,l}(r))^2\), para el orbital 1s.
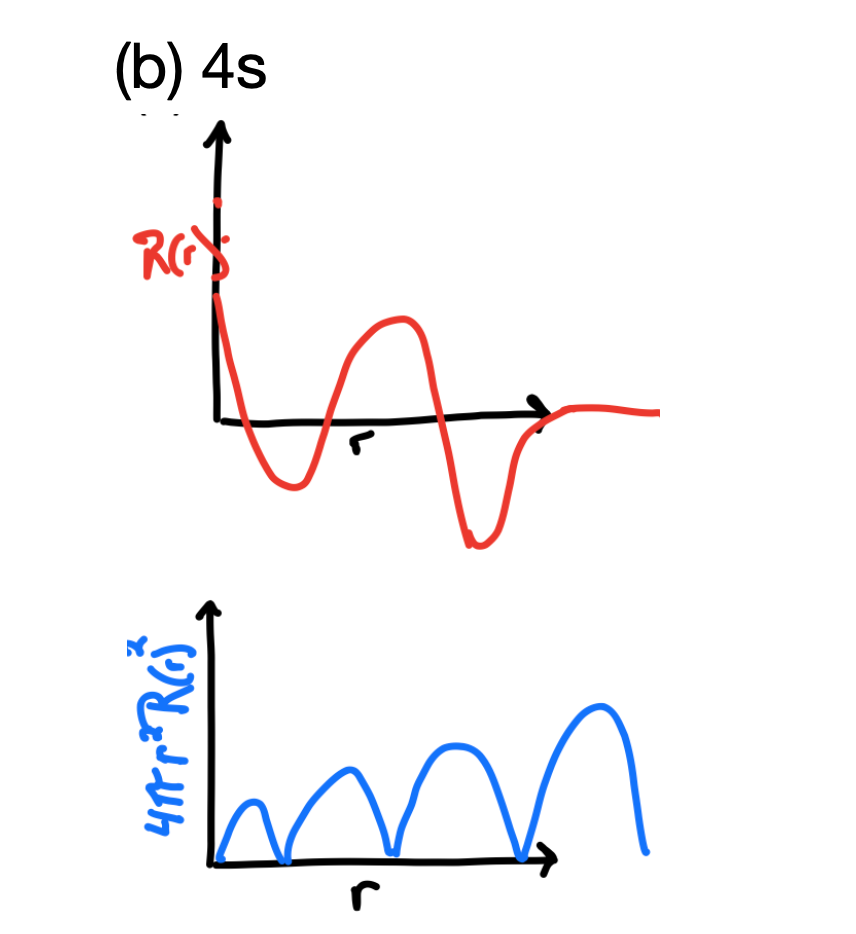
- La función de onda radial,\(R_{n,l}(r)\) y la función de densidad de probabilidad\(4 \pi r^2(R_{n,l}(r))^2\), para el orbital 4s.
- Respuesta, 1s
-
Los orbitales 1s\(R_{n,l}(r)\) alcanzan un máximo cerca del origen y se aproximan a cero lejos del núcleo. El\(4 \pi r^2(R_{n,l}(r))^2\) se aproxima a cero en el origen, tiene una intensidad máxima en el radio de Bohr y se acerca a cero lejos del núcleo (su superficie límite).
.
- Respuesta, 4s
-
Como todos los orbitales s, los orbitales 4s\(R_{n,l}(r)\) alcanzan un máximo cercano a X=0, pero sería menos intenso que la función de los orbitales 1s, 2s y 3s. Debería tener tres nodos radiales y así su función ondulada cambiaría de signo tres veces. Esto daría cuatro regiones de densidad electrónica en la función de probabilidad mientras que la función se acercaría a cero (superficie límite) lejos del núcleo.
Contribución angular\(\textcolor{red}{Y_{l,m_l}(\theta,\phi)}\), y función de probabilidad angular,\(\textcolor{red}{(Y_{l,m_l}(\theta,\phi))^2}\)
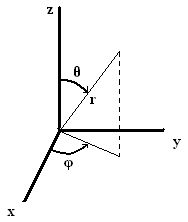La contribución angular a la función de onda\(\textcolor{red}{Y_{l,m_l}(\theta,\phi)}\), describe la forma de la función de onda, o el ángulo con respecto a un sistema de coordenadas. Para describir la dirección en el espacio, utilizamos coordenadas esféricas que nos indican distancia y orientación en el espacio tridimensional. Hay tres coordenadas esféricas:\(r, \phi,\) y\(\theta\). \(r\)es el radio, o la distancia real desde el origen. \(\phi\)y\(\theta\) son ángulos. \(\phi\)se mide desde el eje x positivo en el plano xy y puede estar entre 0 y\(2\pi\). \(\theta\)se mide desde el eje z positivo hacia el plano xy y puede estar entre 0 y\(\pi\).
\[\textcolor{red}{Y_{l,m_l}(\theta,\phi)}=\left ( \dfrac{1}{4\pi} \right )^{1/2}y\left (\theta,\phi \right ) \nonumber \]
\(\textcolor{red}{Y_{l,m_l}(\theta,\phi)}\), es un poco más difícil de describir que la contribución radial. Esto se debe en parte a que\(\textcolor{red}{Y_{l,m_l}(\theta,\phi)}\) contiene números imaginarios, que no tienen un significado real, físico. Sin embargo, la parte angular de la función de onda se vuelve más “real” cuando la cuadras para obtener densidad de probabilidad angular, un concepto más tangible descrito como las formas de los orbitales.
Los valores de\(\theta\),\(\phi\), y\(y(\theta,\phi)\) para orbitales en el átomo de hidrógeno se enumeran en la Tabla\(\PageIndex{3}\). Pero\(Y_{l,m_l}(\theta,\phi)\) es sólo una función matemática y no tiene ningún significado físico real. El cuadrado de la función de onda radial,\(Y_{l,m_l}(\theta,\phi)^2\), da la probabilidad de encontrar el electrón en un punto en el espacio sobre un rayo descrito por\((\phi, \theta)\). Así\(Y_{l,m_l}(\theta,\phi)^2\) describe la forma de la órbita.
| subshell | \(m_l\)(orbital) | \(\theta\) | \(\phi\) | Parcelas de\(\theta^2\) | formas orbitales |
|---|---|---|---|---|---|
| \(l=0\), s | \ (m_l\) (orbital) ">\(m_l=0\) | \ (\ theta\) ">\(\frac{1}{\sqrt{2}}\) | \ (\ phi\) ">\(\frac{1}{\sqrt{2 \pi}}\) | \ (\ theta^2\) "> |
 |
| \(l=1\), p | \ (m_l\) (orbital) ">\(m_l=0\) | \ (\ theta\) ">\(\frac{\sqrt{6}}{2} \cos \theta\) | \ (\ phi\) ">\(\frac{1}{\sqrt{2 \pi}}\) | \ (\ theta^2\) "> |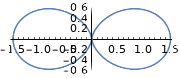
 |
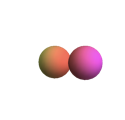| \(l=1\), p | \ (m_l\) (orbital) ">\(m_l=+1\) | \ (\ theta\) ">\(\frac{\sqrt{3}}{2} \sin \theta\) | \ (\ phi\) ">\(\frac{1}{\sqrt{2 \pi}} e^{i \phi}\) | \ (\ theta^2\) "> |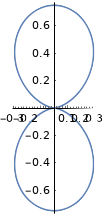
 |
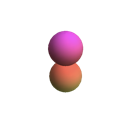| \(l=1\), p | \ (m_l\) (orbital) ">\(m_l=-1\) | \ (\ theta\) ">\(\frac{\sqrt{3}}{2} \sin \theta\) | \ (\ phi\) ">\(\frac{1}{\sqrt{2 \pi}} e^{-i \phi}\) | \ (\ theta^2\) "> |
 |
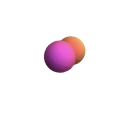| \(l=2\), d | \ (m_l\) (orbital) ">0 | \ (\ theta\) ">\(\frac{\sqrt{10}}{4}\left(3 \cos ^{2} \theta-1\right)\) | \ (\ phi\) ">\(\frac{1}{\sqrt{2 \pi}}\) | \ (\ theta^2\) "> |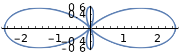
 |
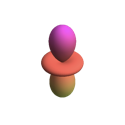| \(l=2\), d | \ (m_l\) (orbital) ">\(m_l=+1\) | \ (\ theta\) ">\(\frac{\sqrt{15}}{2} \sin \theta \cos \theta\) | \ (\ phi\) ">\(\frac{1}{\sqrt{2 \pi}} e^{i \phi}\) | \ (\ theta^2\) "> |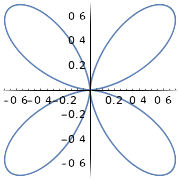
 |
| \(l=2\), d | \ (m_l\) (orbital) ">\(m_l=-1\) | \ (\ theta\) ">\(\frac{\sqrt{15}}{2} \sin \theta \cos \theta\) | \ (\ phi\) ">\(\frac{1}{\sqrt{2 \pi}} e^{-i \phi}\) | \ (\ theta^2\) "> |
 |
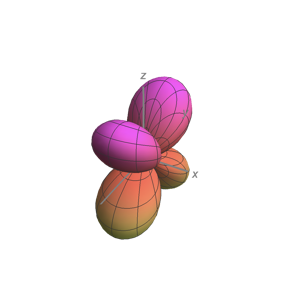| \(l=2\), d | \ (m_l\) (orbital) ">\(m_l=+2\) | \ (\ theta\) ">\(\frac{\sqrt{15}}{4} \sin ^{2} \theta\) | \ (\ phi\) ">\(\frac{1}{\sqrt{2 \pi}} e^{i 2 \phi}\) | \ (\ theta^2\) "> |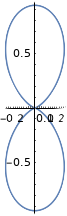
 |
| \(l=2\), d | \ (m_l\) (orbital) ">\(m_l=-2\) | \ (\ theta\) ">\(\frac{\sqrt{15}}{4} \sin ^{2} \theta\) | \ (\ phi\) ">\(\frac{1}{\sqrt{2 \pi}} e^{-i 2 \phi}\) | \ (\ theta^2\) "> |
 |
Nodos angulares
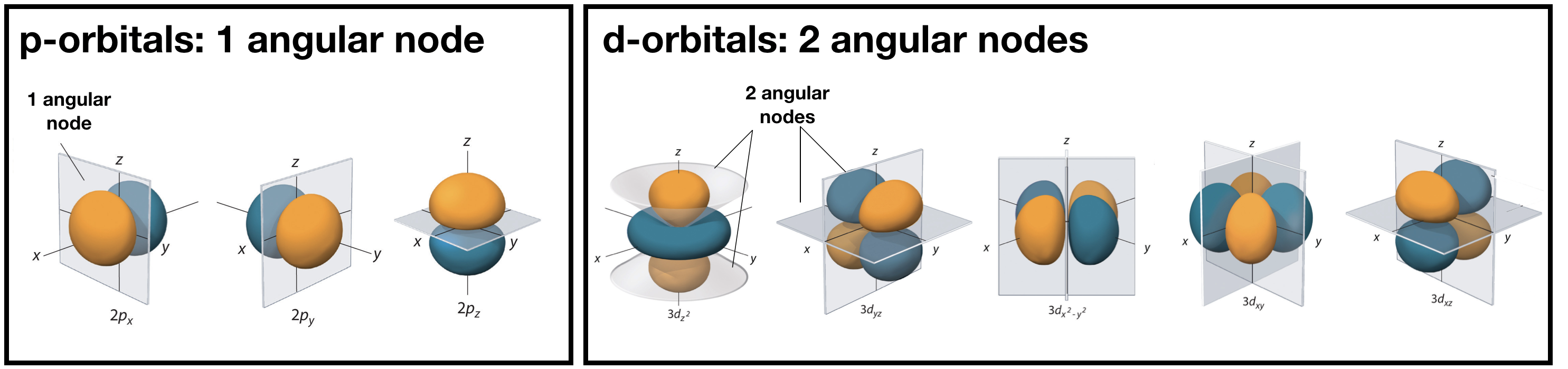
Los nodos angulares existen donde\(\textcolor{red}{(Y_{l,m_l}(\theta,\phi))^2}=0\). Estos nodos son planos en forma, y dependen del valor de\(l\). El número de nodos angulares en cualquier orbital es igual a\(l\). Esto significa que los orbitales s (\(l=0\)) tienen cero nodos angulares, los orbitales p (\(l=1\)) tienen un nodo angular, los orbitales d (\(l=2\)) tienen dos nodos angulares, y así sucesivamente. Los nodos planos pueden ser planos (como los nodos en todos los orbitales p) o pueden tener una forma cónica, como los dos nodos angulares en la\(d_{Z^2}\) órbita. Los nodos angulares en algunos orbitales p y d se muestran en la Figura\(\PageIndex{4}\).
Orbitales atómicos
Los orbitales atómicos son el resultado de una combinación de las contribuciones radiales y angulares de la función ondulada. Los orbitales atómicos pueden tener tanto nodos angulares como radiales, dependiendo de los valores de\(n\) y\(l\).
La siguiente tabla compara la variación radial, la variación angular y sus combinaciones (orbitales).
| Orbital | Probabilidad Radial | Nodos Radiales | Probabilidad Angular | Nodos Angulares |
Combinación (Orbital) |
Nodos Totales |
|---|---|---|---|---|---|---|
| 1s |  |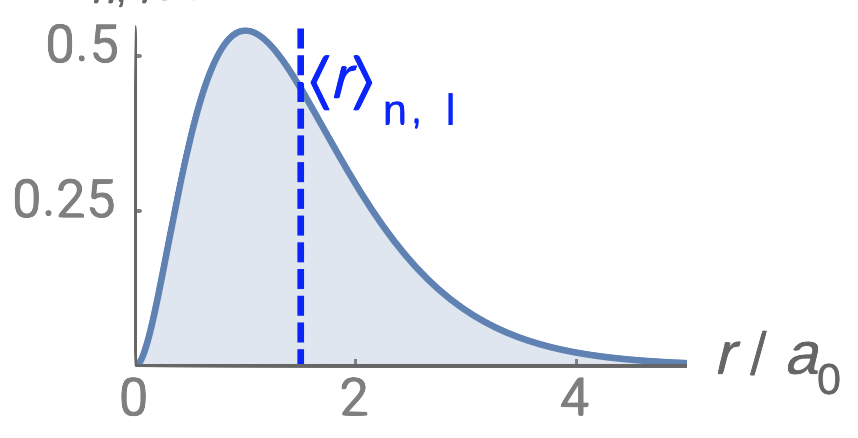
0 | |
0 |  |
0 |
| 2s |  |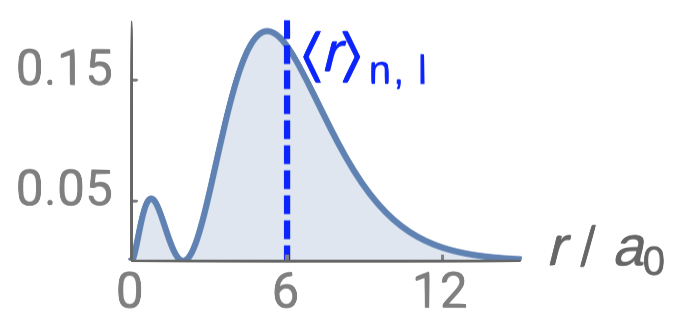
1 | |
0 |  |
1 |
| 2p |  |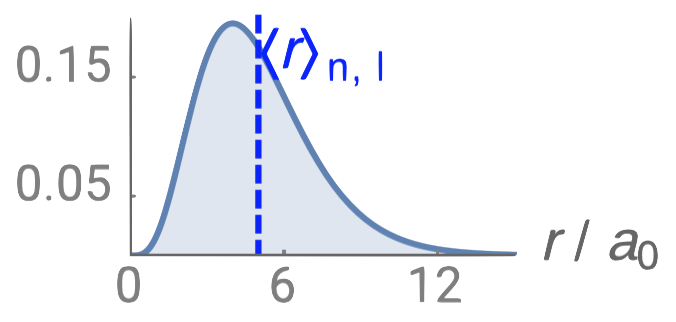
0 | |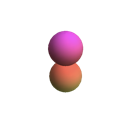
1 |  |
1 |
| 3s |  |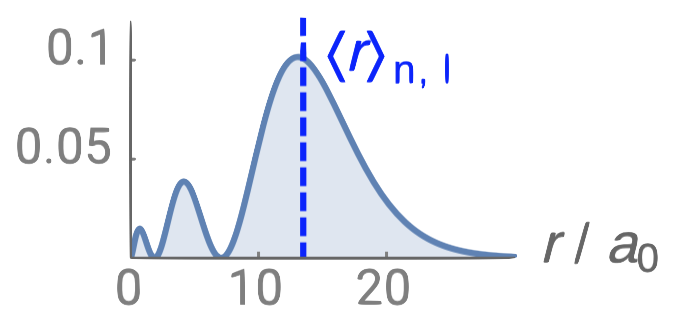
2 | |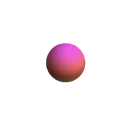
0 |  |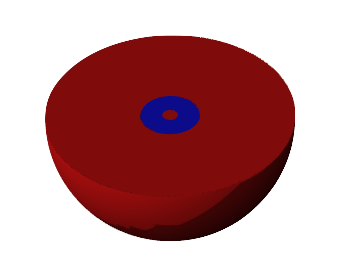
2 |
| 3p |  |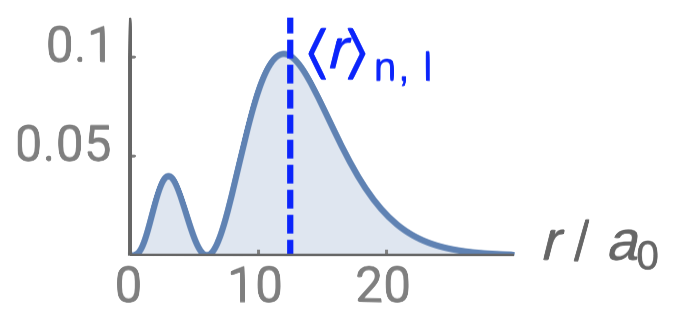
1 | |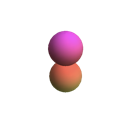
1 |  |
2 |
| 3d |  |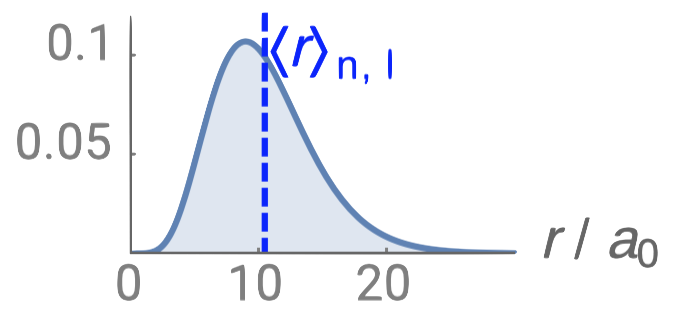
0 | |
2 |  |
2 |