4.3.2: Representaciones de Grupos de Puntos

Operaciones de simetría: representaciones matriciales

Una operación de simetría, como una rotación alrededor de un eje de simetría o una reflexión a través de un plano, es una operación que, cuando se realiza sobre un objeto, da como resultado una nueva orientación del objeto que es indistinguible del original. Por ejemplo, si giramos un cuadrado en el plano por\(\pi/2\) o\(\pi\), la nueva orientación del cuadrado es superpuesta sobre la original (Figura\(\PageIndex{1}\)).

Si la rotación por un ángulo\(\theta\) de una molécula (u objeto) alrededor de algún eje da como resultado una orientación de la molécula (u objeto) que se superpone sobre el original, el eje se denomina eje de rotación. Se dice que la molécula (u objeto) tiene un eje de rotación\(n\) -fold, donde\(n\) está\(2\pi/\theta\). El eje se denota como\(C_n\). El cuadrado de la Figura\(\PageIndex{1}\) tiene un\(C_4\) eje perpendicular al plano debido a que una\(90^{\circ}\) rotación deja la figura indistinguible de la orientación inicial. Este eje también es un\(C_2\) eje porque una rotación de\(180^{\circ}\) grados deja el cuadrado indistinguible del cuadrado original. Además, la figura tiene varios otros\(C_2\) ejes que se encuentran en el mismo plano que el cuadrado:

Figura\(\PageIndex{1}\): Operaciones de simetría realizadas en un cuadrado

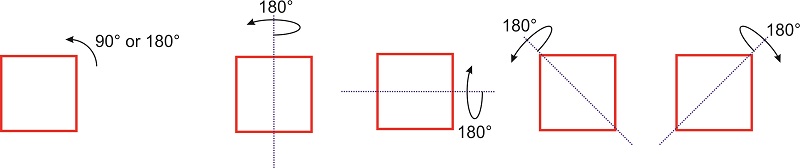
Una operación de simetría mueve todos los puntos del objeto de una posición inicial a una posición final, y eso significa que los operadores de simetría son matrices\(3\times 3\) cuadradas (o\(2\times 2\) en dos dimensiones). Cada operación de simetría se puede expresar como una matriz de transformación donde el vector\((x',y',z')\) representa las nuevas coordenadas del punto\((x,y,z)\) después de la operación de simetría.

\[[\text{New Coordinates} (x',y',z')] = [\text{Transformation Matrix}] \times [\text{Old Coordinates} (x,y,z)] \nonumber \]

Utilizaremos el ejemplo del agua, que está en el grupo de\(C_{2v}\) puntos, para ilustrar cómo se pueden utilizar las matrices de transformación para representar la simetría de un grupo.

La figura\(\PageIndex{2}\) muestra los tres elementos de simetría de la molécula de agua (H\(_2\) O). Esta molécula tiene sólo un eje de rotación, que es de 2 veces, y por lo tanto la llamamos un “\(C_2\)eje”. También tiene dos planos espejo, uno que contiene los dos átomos de hidrógeno (\(\sigma_{yz}\)), y otro perpendicular a él (\(\sigma_{xz}\)). Ambos planos contienen el\(_2\) eje C.

Figura\(\PageIndex{2}\): Los elementos de simetría de la molécula de agua

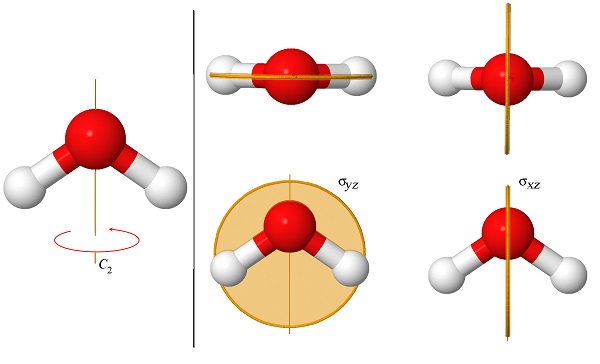
Matriz de transformación de\(C_2\) rotación

Una rotación de 2 veces alrededor del\(z-\) eje cambia la ubicación de un punto\((x,y,z)\) a\((-x,-y,z)\) (ver Figura\(\PageIndex{3}\)). Por convención, las rotaciones siempre se toman en sentido contrario a las agujas del reloj.

Figura\(\PageIndex{3}\): Una rotación de 2 veces alrededor del\(z\) eje

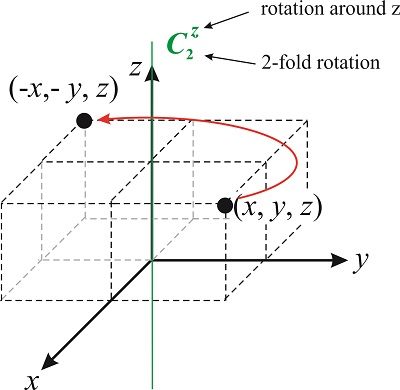
¿Cuál es la matriz que representa la\(C_2\) rotación? La matriz transforma el vector\((x,y,z)\) en\((-x,-y,z)\), entonces

\[{C_2}(x,y,z)=(-x,-y,z) \nonumber \]

\[\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} -x \\ -y \\ z \end{pmatrix} \nonumber \]

Sabemos que la matriz es una matriz\(3\times 3\) cuadrada porque necesita multiplicar un vector tridimensional. Además, escribimos el vector como columna vertical para satisfacer los requisitos de multiplicación matricial.

\[\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix} \nonumber \]

\[a_{11}x+a_{12}y+a_{13}z=-x \nonumber \]

\[a_{21}x+a_{22}y+a_{23}z=-y \nonumber \]

\[a_{31}x+a_{32}y+a_{33}z=z \nonumber \]

y concluimos que\(a_{11}=-1\),\(a_{12}=a_{13}=0\),\(a_{22}=-1\),\(a_{21}=a_{23}=0\) y\(a_{33}=1\),\(a_{31}=a_{32}=0\). La matriz de transformación de la\(C_2\) operación del grupo de\(C_{2v}\) puntos es:

\[C_2=\begin{pmatrix} -1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber \]

Matriz de transformación de\(\sigma_{xz}\) reflexión

Las rotaciones no son las únicas operaciones de simetría que podemos realizar en una molécula. La figura\(\PageIndex{4}\) ilustra la reflexión de un punto a través del\(xz\) plano. Esta operación transforma el vector\((x,y,z)\) en el vector\((x,-y,z)\). Los operadores de simetría que involucran reflexiones a través de un plano generalmente se denotan con la letra\(\sigma\), por lo que el operador que refleja un punto a través del\(xz\) plano es\(\hat{\sigma}_{xz}\):

\[\sigma_{xz}(x,y,z)=(x,-y,z) \nonumber \]

Figura\(\PageIndex{3}\): Una reflexión a través del\(xz\) plano

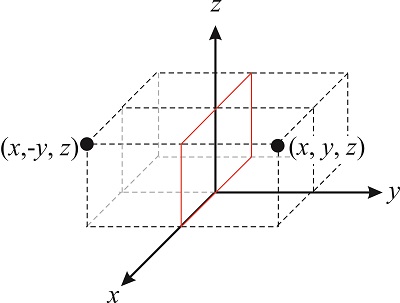
Siguiendo la misma lógica que usamos para la matriz de rotación, podemos escribir la matriz de\(\sigma_{xz}\) transformación como:

\[\sigma_{x,z}=\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber \]

Esto es cierto porque

\[\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} x \\ -y \\ z \end{pmatrix} \nonumber \]

Ejercicio\(\PageIndex{1}\)

Encuentra la matriz de transformación de la identidad (E) y las\(\sigma_{y,z}\) operaciones bajo el grupo de\(C_{2v}\) puntos.

Contestar

La matriz de transformación para\(E\) is\(\begin{pmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\).

La matriz de transformación para\(\sigma_{v(yz)"}\) is\(\begin{pmatrix} -1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\).

Personajes

Para una matriz cuadrada, el carácter es el rastro de la matriz. Para la\(C_2\) operación, con la matriz de transformación

\[\begin{pmatrix} -1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix}, \nonumber \]

el rastro es\((-1) + (-1) + 1 = -1\).

El conjunto de caracteres para un grupo de puntos se denomina representación reducible (\(\Gamma\)). La representación reducible para el grupo de\(C_{2v}\) puntos es:

\[\begin{array}{l|llll} C_{2v} & E & C_2 & \sigma_v & \sigma_v' \\ \hline \Gamma & 3 & -1 & 1 & 1 \end{array} \nonumber \]

Ejercicio\(\PageIndex{1}\)

Demostrar que los caracteres en la representación reducible para\(C_{2v}\) son correctos:

\[\begin{array}{l|llll} C_{2v} & E & C_2 & \sigma_v & \sigma_v' \\ \hline \Gamma & 3 & -1 & 1 & 1 \end{array} \nonumber \]

Contestar

Para la\(E\) operación, con la matriz de transformación\(\begin{pmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\), la traza es\(1 + 1 + 1 = \)\(3\).

Para la\(C^z_2\) operación, con la matriz de transformación\(\begin{pmatrix} -1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber\), la traza es\((-1) + (-1) + 1 =\)\( -1\).

Para la\(\sigma_{v(xz)'}\) operación, con la matriz de transformación\(\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber\), la traza es\(1 + (-1) + 1 =\)\(1\).

Para la\(\sigma_{v(yz)"}\) operación, con la matriz de transformación\(\begin{pmatrix} -1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\), la traza es\(-1 + 1 + 1 =\)\(1\).

Esto da la representación reducible\(\begin{array}{l|llll} C_{2v} & E & C_2 & \sigma_v & \sigma_v' \\ \hline \Gamma & 3 & -1 & 1 & 1 \end{array} \)

Representaciones reducibles e irreducibles

Ahora volvamos y veamos con más detalle las matrices de transformación del\(C_{2v}\) point group that we derived above. If we look at the matrices carefully we see that they all take the same block diagonal form (a square matrix is said to be block diagonal if all the elements are zero except for a set of submatrices lying along the diagonal).

\[E=\begin{pmatrix} {\color{red}[1]}&0&0 \\ 0&{\color{blue}[1]}&0 \\ 0&0&{\color{green}[1]} \end{pmatrix}, \, C_2=\begin{pmatrix} {\color{red}[-1]}&0&0 \\ 0&{\color{blue}[-1]}&0 \\ 0&0&{\color{green}[1]} \end{pmatrix} ,\, \sigma_{v(xz)}'=\begin{pmatrix} {\color{red}[1]}&0&0 \\ 0&{\color{blue}[-1]}&0 \\ 0&0&{\color{green}[1]} \end{pmatrix} ,\, \sigma_{v(yz)"}=\begin{pmatrix} \color{red}[-1]&0&0 \\ 0&{\color{blue}[1]}&0 \\ 0&0&{\color{green}[1]} \end{pmatrix} \nonumber \]

Todos los elementos distintos de cero se convierten en matrices 1x1 que representan cada una de ellas\({\color{red}x}, {\color{blue}y}, {\color{green}z}\) coordenadas individuales. En otras palabras, el elemento\(\color{red}a_{11}\) representa\(\color{red}x\)\(\color{blue}y\),\(\color{blue}a_{22}\) representa y\(\color{green}a_{33}\) representa\(\color{green}z\). Los elementos de la matriz para x de cada matriz de transformación se combinan para formar una representación irreducible del grupo de\(C_{2v}\) puntos. Asimismo, los elementos de la matriz para y se combinan para formar una segunda representación irreducible, y lo mismo es cierto para los elementos z. Estas representaciones irreducibles se muestran a continuación:

\[\begin{array}{l|llll|l} C_{2v} & E & C_2 & \sigma_v & \sigma_v' & \text{Coordinate Used}\\ \hline & \color{red}1 & \color{red}-1&\color{red}1&\color{red}-1 & \color{red}x \\ & \color{blue}1 & \color{blue}-1 & \color{blue}-1 & \color{blue}1 & \color{blue}y \\ & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}z\\ \hline \Gamma & 3 & -1 & 1 & 1 \end{array} \nonumber \]

Las representaciones irreducibles se suman para formar la representación reducible,\(\Gamma\). Este\(\Gamma\), que es el conjunto de matrices 3x3, se puede reducir al conjunto de matrices 1x1 de las representaciones irreducibles. Las representaciones irreducibles no pueden reducirse más, de ahí su nombre.

Fuentes y atribución

• Parts of this page was adapted from Matrices (click here) (Symmetry Operators), contributed by Marcia Levitus, Associate Professor (Biodesign Institute) at Arizona State University.
• Parts of this page were adapted from Reductions of Representations, contributed by

  Claire Vallance (University of Oxford)

• Modified by Kathryn Haas (khaaslab.com)