4.3.3: Tablas de caracteres

Introducción a las Tablas de Caracteres, usando\(C_{2v}\) como ejemplo

Una tabla de caracteres es el conjunto completo de representaciones irreducibles de un grupo de simetría. En el apartado anterior, derivamos tres de las cuatro representaciones irreducibles para el grupo de\(C_{2v}\) puntos. Estas tres representaciones irreducibles están etiquetadas\(A_1\),\(B_1\), y\(B_2\). La cuarta representación irreducible,\(A_2\), se puede derivar usando las propiedades (o “reglas”) para representaciones irreducibles que se enumeran a continuación.

Propiedades de Caracteres de Representaciones Irreducibles en Grupos de Puntos

1. Siempre hay una representación totalmente simétrica en la que todos los personajes son 1.
   ej.\(C_{2v}\), In,\(A_1\) es totalmente simétrico.
2. El orden del grupo (\(h\)) es el número total de operaciones de simetría en el grupo.
   por ejemplo\(C_{2v}\), en,\(h=4\)
3. Operaciones similares se listan como clases (R) y aparecen como columnas en la tabla.
   Por ejemplo\(C_{2v}\), en, hay cuatro clases de operaciones\(E\),\(C_2\),\(\sigma_{v(xz)}\), y\(\sigma_{v(yz)}'\)
4. El número de representaciones irreducibles (filas) debe ser igual al número de clases (columnas). Esto da como resultado que todas las tablas de caracteres sean cuadradas.
   e.g. En\(C_{2v}\), hay cuatro clases y cuatro representaciones irreducibles.
5. La suma de cuadrados de todos los caracteres bajo\(E\) es igual al orden del grupo:\(h = \sum [\chi_i]^2\)
   por ejemplo\(C_{2v}\), In,\(h = 1^2 + 1^2 +1^2 +1^2 = 4\)
6. Para cualquier representación irreducible (\(i\)), la suma de cuadrados de sus caracteres multiplicada por el número de operaciones en la clase es el orden del grupo:\(h = \sum [\chi_i(R)]^2\)
   por ejemplo, For\(A_2\) in\(C_{2v}\),\(h = (1\times 1)^2 + (1\times 1)^2 +(-1\times 1)^2 +(-1\times 1)^2 = 4\)
7. Las representaciones irreducibles son ortogonales. Para dos representaciones cualesquiera (\(i\)y\(j\)):\(\sum [\chi_i*(R)\chi_j(R)] = 0\)
   por ejemplo, Para\(\color{red}B_1\) y\(\color{blue}B_2\) de\(C_{2v}\),\([{\color{red}1} \times {\color{blue}1}] + [{\color{red}-1} \times {\color{blue}-1}] + [{\color{red}1} \times {\color{blue}-1}] + [{\color{red}-1} \times {\color{blue}1}] = 0\)

La tabla completa de caracteres para\(C_{2v}\) se da a continuación.

\(\begin{array}{l|llll|l|l} C_{2v} & E & C_2 & \sigma_v & \sigma_v' & h=4\\ \hline \color{green}A_1 & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}z & x^2,y^2,z^2\\ \color{purple}A_2 & \color{purple}1 & \color{purple}1 & \color{purple}-1 & \color{purple}-1 & R_z & xy \\ \color{red}B_1 & \color{red}1 & \color{red}-1&\color{red}1&\color{red}-1 & {\color{red}x},R_y & xz \\ \color{blue}B_2 & \color{blue}1 & \color{blue}-1 & \color{blue}-1 & \color{blue}1 & {\color{blue}y} ,R_x & yz \end{array} \)

Las distintas secciones de la tabla son las siguientes:

• El primer elemento de la tabla da el nombre del grupo de puntos, generalmente en Schoenflies (\(C_{2v}\)) notation.
• A lo largo de la primera fila se encuentran las operaciones de simetría del grupo,\(E\), \(C_2\), \(\sigma_v\) and \(\sigma_v"\), followed by the order of the group, \(h\).
• En la primera columna se encuentran las representaciones irreducibles del grupo, representadas por Etiquetas Mulliken. En\(C_{2v}\) the irreducible representations are \(A_1\), \(A_2\), \(B_1\) and \(B_2\). The Mulliken labels indicate the symmetry of each representation (explained further below).
• Los personajes (\(\chi\)) of the irreducible representations under each symmetry operation are given in the bulk of the table.
• La (s) columna (s) final (s) de la tabla enumera una serie de funciones que se transforman como las diversas representaciones irreducibles del grupo. Estos son los ejes cartesianos\(\begin{pmatrix} x, y, z \end{pmatrix}\), the Cartesian products \(\begin{pmatrix} z^2, x^2 + y^2, xy, xz, yz \end{pmatrix}\), and the rotations \(\begin{pmatrix} R_x, R_y, R_z \end{pmatrix}\) (explained further below).

Otro ejemplo:\(C_{3v}\)

Th\(C_{3v}\) point group has three classes of operations: \(E\), \(C_{3}\), and \(\sigma_{v(xz)}\). The derivation of transformation matrices for E and \(\sigma_{v(xz)}\) is similar to the case for \(C_{2v}\). However, the \(C_{3v}\) operation does not give simple 1 or -1 characters. If we carry out a rotation about \(z\) by an angle \(\theta\), nuestro\(x\) and \(y\) axes are transformed onto new axes \(x'\) and \(y'\). The new axes can each be written as a linear combination of our original \(x\) and \(y\) axes. The derivation of the rotation matrices will not be covered in this text, but is described elsewhere:

\[\begin{array}{ccc}x' & = & x\cos\theta + y\sin\theta \\ y' & = & -x\sin\theta + y\cos\theta \end{array} \nonumber \]

Para un\(C_3\) rotation counterclockwise through 120° (or \(\frac{2\pi}{3}\)):

\[\begin{array}{ccccc}x' & = & x\cos(2\pi/3) + y\sin(2\pi/3) & = & {\color{orange}-\frac{1}{2}x-\frac{\sqrt{3}}{2}y} \\ y' & = & -x\sin(2\pi/3) + y\cos(2\pi/3) & = & {\color{violet}\frac{\sqrt{3}}{2}x-\frac{1}{2}y} \end{array} \nonumber \]

Las matrices de transformación para operaciones de simetría de\(C_{3v}\) son las siguientes:

\(E=\begin{pmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\)\(C_3=\begin{pmatrix} {\color{orange}[-\frac{1}{2}}&{\color{orange}-\frac{\sqrt{3}}{2}]}&0 \\ {\color{violet}[\frac{\sqrt{3}}{2}}&{\color{violet}-\frac{1}{2}]}&0 \\ 0&0&1 \end{pmatrix} \nonumber\)\(\sigma_{v(xz)}'=\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber\)

La matriz de\(C_3\) transformación contiene entradas fuera de la diagonal y, por lo tanto, no se puede diagonalizar en bloques como matrices 1x1. Sin embargo, las dos primeras líneas se pueden diagonalizar como una 2x2 y la última línea como una matriz 1x1 (Figura\(\PageIndex{1}\)):

Figura\(\PageIndex{1}\): La matriz de\(C_3\) transformación contiene entradas fuera de la diagonal y, por lo tanto, no se puede diagonalizar en bloques como matrices 1x1. Sin embargo, las dos primeras líneas se pueden diagonalizar como una 2x2 y la última línea como una matriz 1x1. (CC-BY-NC-SA; Kathryn Haas)

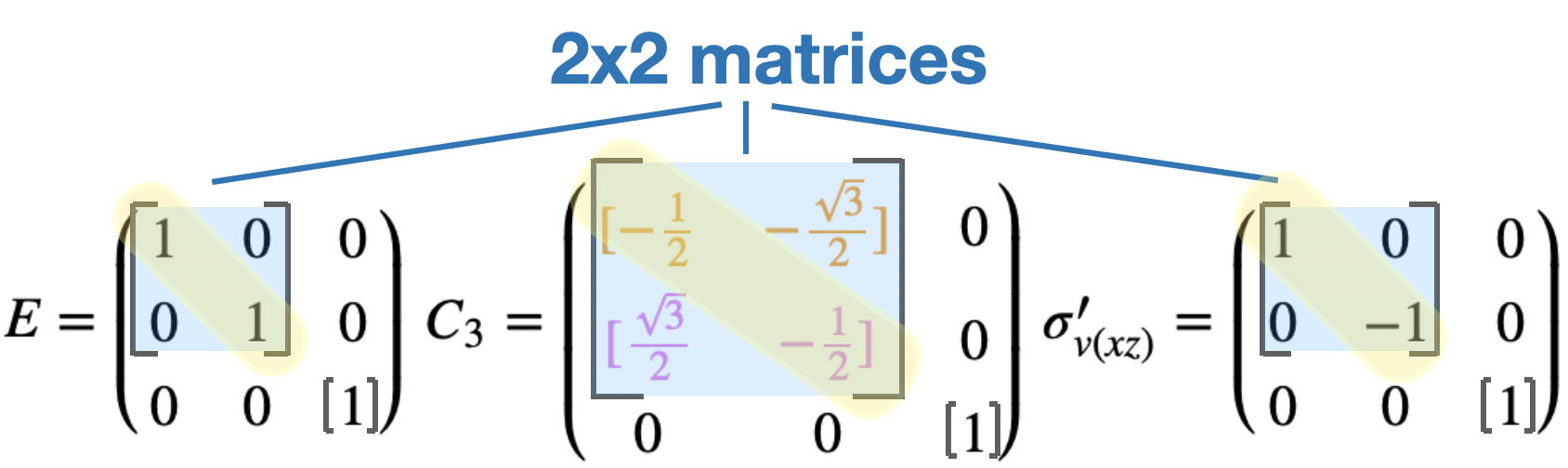
El carácter de una matriz 2x2 es la suma de la traza de esa matriz. Entonces, para la\(C_3\) operación, la matriz 2x2 da el carácter -1 (from\({\color{orange}-\frac{1}{2}} + {\color{violet}-\frac{1}{2}}\)).

La tabla de caracteres para\(C_{3v}\) is shown below.

\(\begin{array}{l|lll|l} \hline C_{3v} & E & 2C_3 & 3\sigma_v & h=6 \\ \hline A_1 & 1 & 1 & 1 & z, z^2, x^2+y^2 \\ A_2 & 1 & 1 & -1 & R_z \\ E & 2 & -1 & 0 & \begin{pmatrix} x, y \end{pmatrix}, \begin{pmatrix} xy, x^2+y^2 \end{pmatrix}, \begin{pmatrix} xz, yz \end{pmatrix}, \begin{pmatrix} R_x, R_y \end{pmatrix} \\ \hline \end{array} \)

Características adicionales de las tablas de caracteres

Características adicionales de las tablas de caracteres

1. Las operaciones de simetría de la misma clase se agrupan en la misma columna (clase) en la tabla de caracteres y no se enumeran por separado.
   e.g. En el grupo de\(C_{3v}\) puntos, hay cuatro operaciones:\(E\),\(C_3\),\(C_3^2\), y\(\sigma_{v}\). Las\(C_3^2\) operaciones\(C_3\) y se enumeran juntas en la tabla de caracteres como\(2C_3\).
2. SI hay varios\(C_2\) ejes (en un\(D\) grupo), los\(C_2\) ejes que son perpendiculares al eje principal se etiquetan con primos (por ejemplo\(C_2'\) y\(C_2''\)); cuando hay múltiples tipos de\(C_2\) ejes perpendiculares, un primo (\(C_2'\)) significa que pasa a través de más átomos, mientras que un doble primo (\(C_2''\)) significa que va entre átomos.
3. Los planos de espejo que son perpendiculares al eje principal son planos especulares “horizontales” y se designan con un\(h\) subíndice (\(\sigma_h\)). Los planos de espejo que están en plano con el eje principal son planos de espejo “verticales”,\(\sigma_v\). Cuando hay dos tipos de planos espejo verticales, los que corren a través de más átomos son\(\sigma_v\) mientras que los que corren entre átomos son “diedros”,\(\sigma_d\).
4. La coincidencia de las operaciones de simetría enumeradas en la tabla de caracteres con las operaciones de simetría de una molécula puede confirmar su grupo de puntos.
5. A las representaciones irreducibles se les asigna una etiqueta Mulliken, listada en la columna de la izquierda, que indica la simetría de esa representación de la siguiente manera:
   \(\begin{array}{l|l} \hline \textbf{Mulliken Labels} & \textbf{meaning}\\ \hline A & \text{singly degenerate (1x1), symmetric to principle axis} \\ B & \text{singly degenerate (1x1), antisymmetric to principle axis} \\ E & \text{doubly degenerate (2x2)} \\ T & \text{triply degenerate (3x3)} \\ \hline \textbf{Subscripts and superscripts} & \textbf{meaning} \\ \hline 1 & \text{symmetric to } \sigma_v \text{or perpendicular to } C_2 \\ 2 & \text{anti-symmetric to } \sigma_v \text{or perpendicular to } C_2 \\ g & \text{symmetric to inversion center} \\ u & \text{anti-symmetric to inversion center} \\ ' & \text{symmetric to } \sigma_h \\ " & \text{anti-symmetric to } \sigma_h \\ \hline \end{array} \)
6. Las columnas de la derecha de la tabla de caracteres enumeran una serie de funciones que se transforman como las diversas representaciones irreducibles del grupo. Estas son las\(\begin{pmatrix} x, y, z \end{pmatrix}\), the Cartesian products \(\begin{pmatrix} z^2, x^2 + y^2, xy, xz, yz \end{pmatrix}\), and the rotaciones de los ejes cartesianos\(\begin{pmatrix} R_x, R_y, R_z \end{pmatrix}\). Estas expresiones indican las propiedades de los orbitales dentro del grupo de simetría. El\(s\) -orbital, que es totalmente simétrico, corresponde a la representación irreducible que posee simetría de\(x^2\),\(y^2\) y\(z^2\) combinada. Cada uno\(p\) de los orbitales posee la simetría del eje correspondiente (por ejemplo,\(p_x\) corresponde al\(x\) eje). Cada uno de los\(d\) -orbitales posee la simetría del producto binario correspondiente (e.g.,\(d_{xy}\) corresponde al producto binario,\(xy\), en la tabla de caracteres).

Las funciones enumeradas en la columna final de la tabla son importantes en muchas aplicaciones químicas de la teoría de grupos, particularmente en espectroscopia. Por ejemplo, al observar las propiedades de transformación de\(x\), \(y\) and \(z\) (sometimes given in character tables as \(T_x\), \(T_y\), \(T_z\)) we can discover the symmetry of translations along the \(x\), \(y\), and \(z\) axes. Similarly, \(R_x\), \(R_y\) and \(R_z\) represent rotations about the three Cartesian axes. The transformation properties of \(x\), \(y\), and \(z\) can be used to determine whether or not a molecule is IR-active or whether or not it can absorb a photon of \(x\)-, \(y\)-, or \(z\)-polarized light and undergo a spectroscopic transition. The Cartesian products play a similar role in determining selection rules for Raman transitions, which involve two photons.

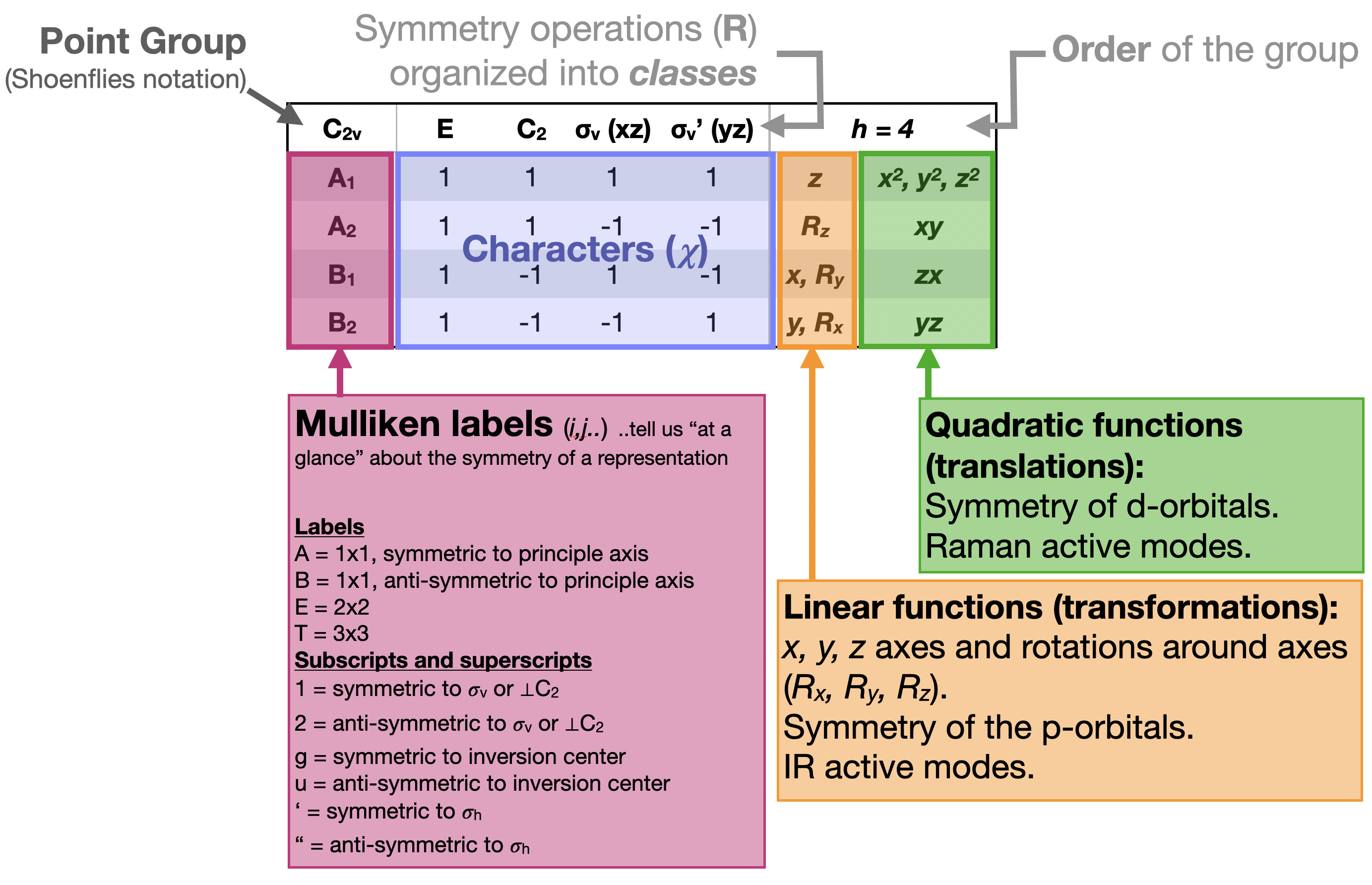
Un resumen visual de las secciones y su significación se da en la Figura\(\PageIndex{2}\). Character tables for common point groups are given in the References section of LibreTexts Bookshelves.

Figura\(\PageIndex{2}\): Resumen visual de las secciones de una tabla de caracteres y su significado. (CC-BY-NC-SA; Kathryn Haas)

Colaboradores y Atribuciones

• Modified by Kathryn Haas (khaaslab.com)

• Claire Vallance (University of Oxford)

  adapted from Character Tables (click here)