5.4.4: NH₃
- Page ID
- 81010
Construye las SALC y el diagrama orbital molecular para\(\ce{NH3}\)
Este es el primer ejemplo hasta el momento que tiene más de dos átomos colgantes y el primer ejemplo en el que la molécula tiene átomos que se encuentran en tres dimensiones (es decir, no es plana). El amoníaco es una molécula piramidal trigonal, con tres átomos de hidrógeno colgantes. La forma tridimensional y el número impar de átomos colgantes hacen que este ejemplo sea más complicado que los casos anteriores de agua, dióxido de carbono y bifluoruro. En este caso, esbozar las formas (paso 5) de las SALC de átomos colgantes es menos sencillo; más bien, se prefiere un método alternativo, el método del operador de proyección, para generar representaciones pictóricas de las SALC.
Como en ejemplos anteriores, es importante recordar que las interacciones de los ligandos colgantes dependen de sus posiciones en el espacio tridimensional. Se debe considerar que las posiciones de los cuatro átomos en amoníaco están esencialmente fijas en relación entre sí. Recorreremos los pasos utilizados para construir el diagrama orbital molecular del amoníaco. Los primeros pasos son los mismos que has visto antes:
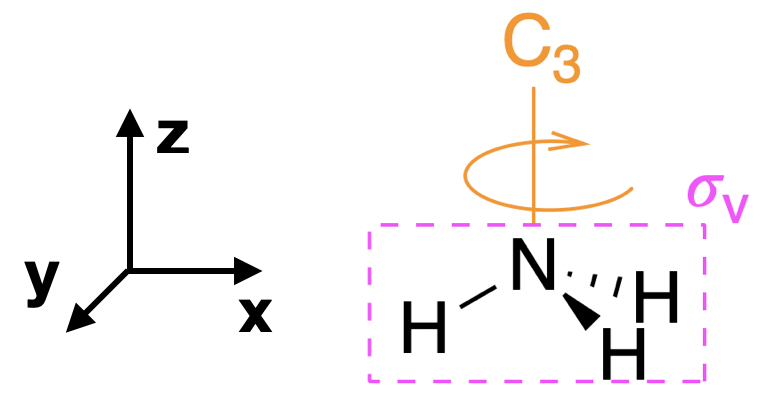
Paso 1. Encuentra el grupo de puntos de la molécula y asigna coordenadas cartesianas para que z sea el eje principal.
La\(_3\) molécula NH es piramidal trigonal y su grupo puntual es\(C_{3v}\). El\(z\) eje es colineal con el eje principal, el\(C_3\) eje.
Paso 2. Identificar y contar los orbitales de valencia de los átomos colgantes.
Cada uno de los tres átomos de hidrógeno colgantes tiene una valencia orbital; la\(1s\). Así, podemos esperar un total de tres SALC de estos tres átomos.
Paso 3. Generar los\(\Gamma\)'s
Usa la tabla de\(C_{3v}\) caracteres para generar una representación reducible (\(\Gamma\)); en este caso solo necesitamos una\(\Gamma\) porque solo hay un tipo de valencia orbital (la\(1s\)). Para cada\(s\) orbital, asigne un valor de 1 si permanece en su lugar durante la operación o cero si se mueve fuera de su lugar original. El\(\Gamma\) se da a continuación:
\[\begin{array}{|c|ccc|} \hline \bf{C_{3v}} & E & 2C_3 & 3\sigma_v \\ \hline \bf{\Gamma_{1s}} & 3 & 0 & 1 \\ \hline \end{array} \nonumber \]
Paso 4. Romper\(\Gamma\) en representaciones irreducibles para SALC individuales
Reducir cada uno\(\Gamma\) en sus representaciones componentes irreducibles. Utilizando cualquiera de los procesos descritos anteriormente, encontramos que el\(\Gamma\) reduce a las dos representaciones irreducibles\(A_1\) y\(E\) bajo el grupo de\(C_{3v}\) puntos.
\ [\ begin {array} {|c|ccc|}\ hline\ bf {C_ {3v}} & E & 2C_3 & 3\ sigma_v\\ hline\ bf {\ gamma_ {1s}} &\ bf 3 &\ bf 0 &\ bf 2\\
A_ {1} & 1 & 1 & 1\
E & 2 & -1 & 0
\ hline\ end {array}\ nonumber\]
Observe que solo encontramos DOS representaciones irreducibles. Pero, de hecho tenemos TRES SALC diferentes. La representación\(E\) irreducible es doblemente degenerada, lo que en este contexto significa que corresponde a dos SALC degeneradas. Así, ya hemos encontrado las simetrías de las tres SALC para el amoníaco: Dos de las SALC son degeneradas con\(E\) simetría bajo el grupo\(C_{3v}\) puntual, mientras que la tercera SALC tiene\(A_1\) simetría.
Paso 5. Esbozar las SALC usando el MÉTODO DE OPERADOR DE
A partir de los primeros cuatro pasos (descritos anteriormente), se han encontrado las simetrías (las representaciones irreducibles) de las tres SALC bajo el grupo de\(C_{3v}\) puntos. Para bosquejar la SALC que corresponde a cada representación irreducible, nuevamente usamos la tabla de\(C_{3v}\) caracteres. Pero ahora introduciremos el método del operador de proyección para derivar la representación superficial de cada SALC.
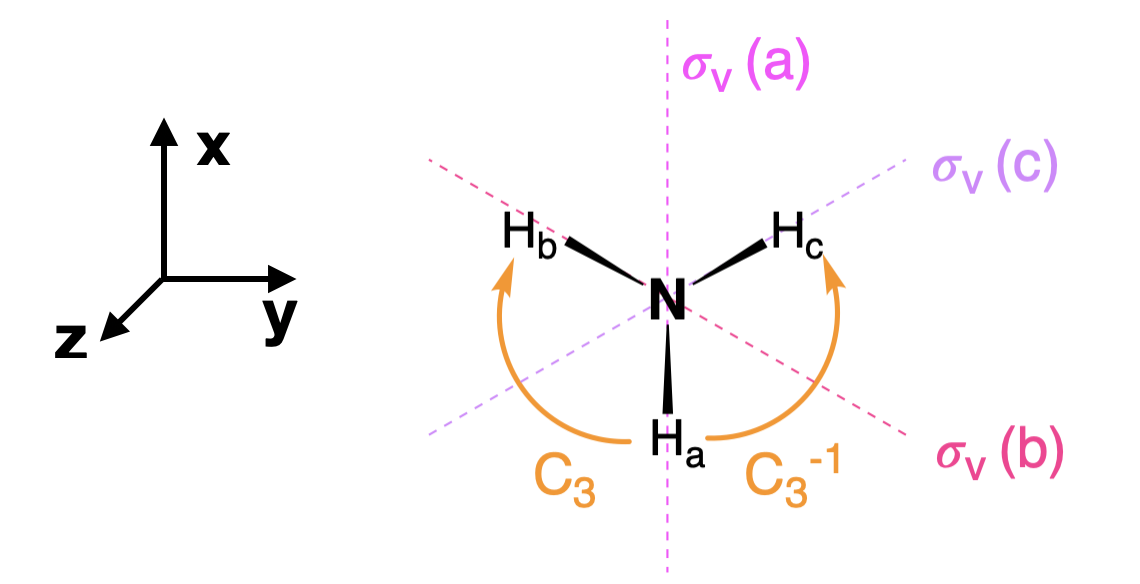
Paso 5.1: Etiquetar los átomos colgantes
En el método del operador de proyección, primero etiquetar cada uno de los átomos colgantes para que podamos distinguir átomos idénticos entre sí; por ejemplo, identificar los tres átomos de hidrógeno en el amoníaco como\(H_a\),\(H_b\), y\(H_c\) (Figura\(\PageIndex{2}\)).
Paso 5.2: Crear una tabla de caracteres expandida con la posición proyectada de un átomo colgante después de cada operación
Realizaremos cada operación del grupo\(C_{3v}\) puntual sobre esta molécula etiquetada y seguiremos donde se proyecta uno de los átomos después de que se complete la operación. Escogeremos arbitrariamente a H\(_a\). Por ejemplo, al realizar la operación de identidad, E, el\(_a\) átomo H se proyecta sobre sí mismo. Por otro lado, H\(_a\) se proyecta\(H_b\) sobre una\(C_3\) rotación en sentido horario (como se dibuja en la Figura\(\PageIndex{2}\)). Tomamos en cuenta el resultado de cada operación utilizando una tabla de caracteres expandida (consulte la siguiente tabla,\ ref {expanded1}). En la tabla de caracteres expandida, cada operación dentro de cada clase se escribe por separado (es decir,\(2C_3\) se contabiliza por separado como\(C_3\) y\(C_3^{-1}\)).
\[\text{Table }\ref{expanded1} \text{: The expanded character table, and the projection of \(H_a\) by each operation is shown below.} \nonumber \]\ [\ begin {array} {|r|cccccc|}\ hline\ bf {C_ {3v}} & E & C_3 & C_3^ {-1} &\ sigma_v (a) &\ sigma_v (b) &\ sigma_v (c)\\ hline\ bf {\ text {Proyección de} H_a} y H_a y H_a _b y H_c y H_a y H_c y H_b\\
\ hline\ final {matriz}\ etiqueta {expanded1}\]
Paso 5.3: Encuentra la contribución de cada átomo colgante a cada SALC
A continuación, crear una combinación lineal de las proyecciones para cada una de las SALC (las representaciones irreducibles que se encuentran en el paso 4). Para cada una de las representaciones irreducibles, multiplique la proyección por el carácter respectivo de la operación.
\[\text{Contribution of each atom to the SALC } = \sum(\text{Projection of }H_a \times \chi) \nonumber \]
La combinación lineal para todas las representaciones irreducibles de\(C_3v\) se muestra a continuación.
\[\text{Table }\ref{expanded2} \text{: The symmetry adapted linear combination (SALC) for each irreducible representation of \(C_3v\) is shown.} \nonumber \]\ [\ begin {array} {|r|cccccc|l|}\ hline\ bf {C_ {3v}} & E & C_3 & C_3^ {-1} &\ sigma_v (a) &\ sigma_v (b) &\ sigma_v (c) &\ text {Combinación Lineal}\\ hline\ bf {\ text {Proyección de} hline\ bf {
\ text {Proyección de} hline\ bf {\ text {Proyección de} hline\ bf {\ text _a} &\ bf h_a &\ bf h_b &\ bf h_c &\ bf h_a &\ bf h_c &\ bf H_b &\\
A-1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & =\ bf 2h_a + 2h_b + 2h_C\\
A_2 & 1 & 1 & 1 & 1 & -1 & -1 & = 0\\
E & 2 & -1 & -1 & 0 & 0 & =\ bf 2h_a - H_b - H_c\
\ hline\ end {array}\ label {expanded2}\]
Observe que solo hay dos representaciones irreducibles que producen SALC, y estas son las mismas que se encontraron en el Paso 4, anterior. Esto ilustra el hecho de que solo las representaciones irreducibles encontradas a través de la reducción de las SALC\(\Gamma\) producirán las SALC. Podemos ignorar cualquier representación irreducible que no se encontró en el Paso 4. O bien, puedes verificar tu trabajo en el Paso 4 aplicando el operador de proyección a cualquier representación irreducible que no se encuentre en el Paso 4, y encontrando que producen una suma de cero.
Paso 5.4: Esbozar las SALC
El significado de las combinaciones lineales que se encuentran en la Tabla\ ref {expanded2} es el siguiente:
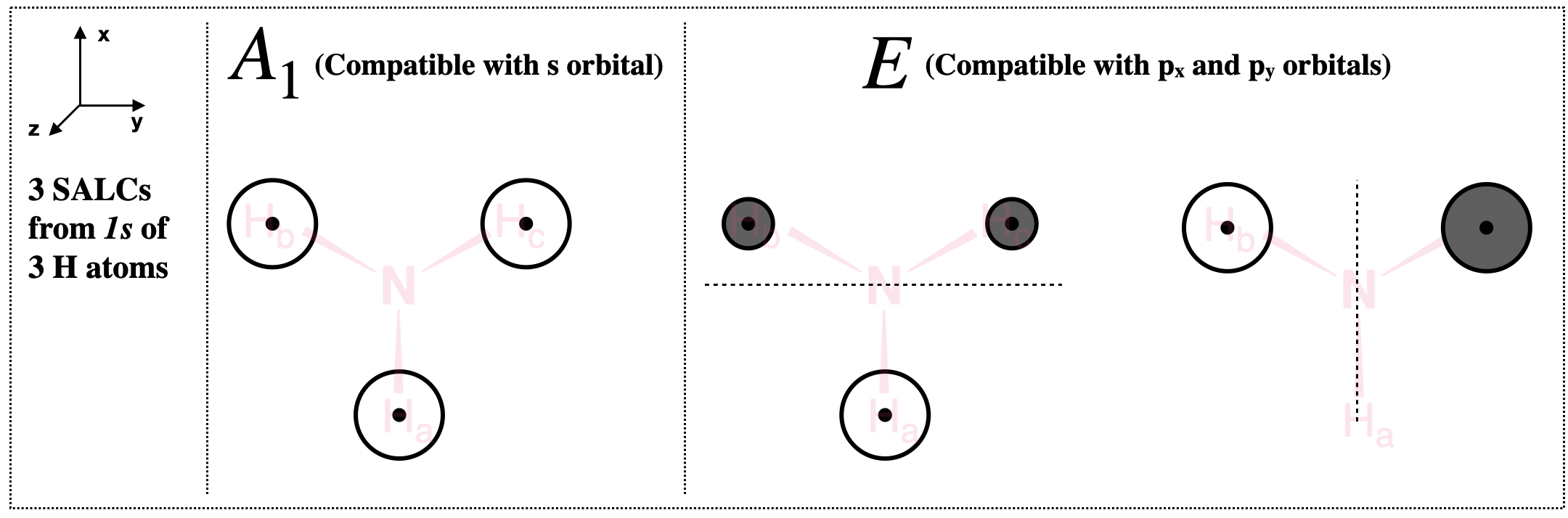
- Esbozar el SALC con\(A_1\) simetría: La combinación lineal\(2H_a + 2H_b + 2H_c\) indica que todas las contribuciones a esta SALC son del mismo signo (de la función de onda). Cualitativamente, esto significa que no hay nodo en este SALC. Podemos tomar esta SALC casi literalmente para asumir que las tres funciones de onda H 1s contribuyen por igual a la SALC. También podemos usar el hecho de que la\(A_1\) representación posee la simetría completa del grupo de\(C_3v\) puntos, es compatible con un orbital s en N, y por lo tanto es un SALC totalmente simétrico.
Cuantitativamente, podemos aplicar el factor normalizador, N, para esta SALC. La combinación lineal para el\(A_1\) SALC en la Tabla\ ref {expanded2} nos muestra que el coeficiente para cada orbital es 1. Así, el factor normalizador para la\(A_1\) SALC es\(N=\left(\frac{1}{\sqrt{1^2 + 1^2 + 1^2}}\right) = \frac{1}{\sqrt{3}}\). Esto nos dice que\(H_a\),\(H_b\), y\(H_c\) cada uno contribuye\(\frac{1}{\sqrt{3}}\) al\(A_1\) grupo normalizado orbital:\[ A_1 \text{ group orbital } = \frac{1}{\sqrt{3}}\left[\psi_{H_{a}}+\psi_{H_{b}}+\psi_{H_{c}}\right] \nonumber \] Esto se muestra visualmente en la Figura\(\PageIndex{3}\). - Esbozar dos SALC con simetría E: La combinación lineal\(2H_a - H_b - H_c\) indica que hay contribuciones con signo positivo y negativo a la función de onda para cada uno de los orbitales\(E\) grupales. Cualitativamente, esto nos dice que hay un nodo dentro de cada una de estas dos SALC, y que la contribución total de la porción positiva de la función de onda es igual a la contribución de la porción negativa.
- Encontrar la primera E SALC:
Para una de las SALC, podemos tomar la combinación lineal de la Tabla\ ref {expanded2} casi literalmente: La contribución de\(H_a\) es igual y opuesta a la suma de las contribuciones de\(H_b + H_c\). Esto daría como resultado un SALC como se muestra en la Figura\(\PageIndex{3}\) (E, izquierda), que tendría simetría del\(x\) eje y que sería compatible con el\(p_x\) orbital en N. El nodo existe en el\(yz\) plano y hay una contribución igual de partes positivas y negativas del total función de onda.
También podemos aplicar el factor normalizador, N, para encontrar esta SALC. La combinación lineal para el\(E\) SALC en la Tabla\ ref {expanded2} nos muestra que los coeficientes para las contribuciones orbitales son 2, -1 y -1. Así, el factor normalizador para la primera\(E\) SALC es\(N=\left(\frac{1}{\sqrt{2^2 + (-1)^2 + (-1)^2}}\right) = \frac{1}{\sqrt{6}}\). Este\(E\) grupo normalizado orbital es:\[\text{First } E \text{ group orbital } = \frac{1}{\sqrt{6}}\left[2\psi_{H_{a}}-\psi_{H_{b}}-\psi_{H_{c}}\right] \nonumber \] Esto se muestra visualmente en la Figura\(\PageIndex{3}\) (E, izquierda). - Encontrar el segundo SALC E:
El segundo SALC es menos obvio a primera vista. Debemos usar pistas de la tabla de caracteres para ayudarnos a determinar cómo debe “verse”. Dado que la\(E\) representación se transforma como el grupo, (\(x,y\)), sabemos que una de las SALC tendrá la simetría del\(x\) eje y\(p_x\) orbital sobre el átomo de nitrógeno central, mientras que la otra debe poseer la simetría del\(y\) eje y ser compatible con el\(p_y\) orbital sobre nitrógeno. Esto por sí solo podría llevarte al boceto del segundo SALC con simetría E que se muestra en la Figura\(\PageIndex{3}\) (E, derecha). Este segundo E SALC debe tener un nodo en el\(xz\) plano, y debido a que\(H_a\) se encuentra en este nodo,\(H_a\) no puede contribuir a este grupo orbital. Conservando el hecho de que las contribuciones positivas y negativas de la combinación lineal deben ser iguales, podemos llegar a una SALC que tiene contribuciones iguales pero opuestas de\(H_b\) y\(H_c\), y ninguna contribución por\(H_c\) (Figura\(\PageIndex{3}\), derecha).
También podemos aplicar el factor normalizador, N, para encontrar esta SALC. Pero hay que aplicar el hecho de que\(H_a\) no puede contribuir a la SALC con "\(y\)" simetría. Eliminamos la contribución de\(H_a\), dejándonos con coeficientes de 0 para\(H_a\) y\(1\) para\(H_b\) y\(H_c\). Así, el factor normalizador para la segunda\(E\) SALC es\(N=\left(\frac{1}{\sqrt{0^2 + 1^2 + 1^2}}\right) = \frac{1}{\sqrt{2}}\). A esto, debemos sumar coeficientes positivos y negativos para que se normalice toda la función de onda de esta SALC. El resultado para este\(E\) grupo normalizado orbital es:\[\text{Second } E \text{ group orbital } = \frac{1}{\sqrt{2}}\left[\psi_{H_{b}}-\psi_{H_{c}}\right] \nonumber \] Esto se muestra visualmente en la Figura\(\PageIndex{3}\).
- Encontrar la primera E SALC:
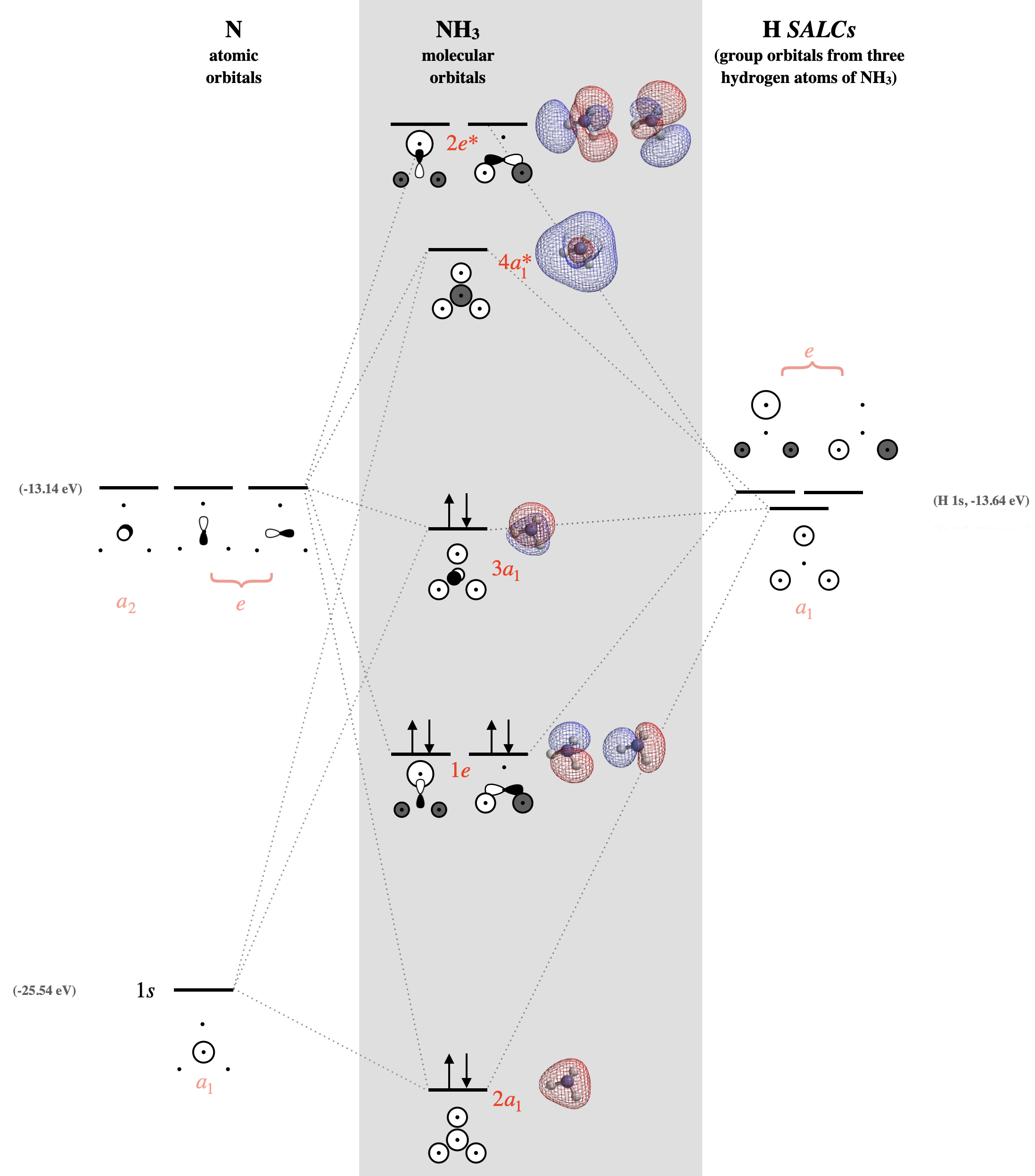
Paso 6. Combina SALC con AO de simetría similar para dibujar el diagrama MO para\(\ce{NH_3}\)
Primero debemos identificar los orbitales de valencia en el nitrógeno central: hay cuatro incluyendo\(2s\),\(2p_x\),\(2p_y\), y\(2p_z\). Ahora identificamos la simetría de cada uno usando la tabla de\(C_{3v}\) caracteres. La simetría de un\(2s\) orbital central corresponde a la combinación de funciones\(x^2\),\(y^2\), y\(z^2\) en la tabla de caracteres; esto es\(A_1\). El\(p_z\) orbital también corresponde a\(A_1\). Y así sucesivamente... A continuación se enumeran las simetrías de los orbitales de valencia de nitrógeno. \[2s =A_1 \\ (2p_x, \; 2p_y) = E \\ 2p_z = A_1 \nonumber \]
El siguiente paso es tener una idea de las energías relativas de los orbitales atómicos de valencia para nitrógeno e hidrógeno, y luego construir el diagrama orbital molecular. La\(2s\) órbita de nitrógeno es aproximadamente 12 eV menor en energía que una H\(1s\). Esta diferencia es una coincidencia de energía aceptable para que los orbitales H interactúen, pero por lo general no resultaría en una interacción fuerte. Por otro lado, los orbitales 2p de nitrógeno tienen una energía muy cercana a los 1s de hidrógeno, diferente en solo 0.5 eV. El conocimiento de las energías relativas de los orbitales atómicos nos dice que, al construir un diagrama, podemos colocar las H SALC a una energía similar a la de los\(2p\) orbitales N, mientras que el N\(2s\) es mucho menor (Figura\(\PageIndex{4}\)).
Los\(2p_z\) orbitales\(2s\) y tienen\(A_1\) simetría y pueden combinarse con el\(A_1\) SALC. Estos orbitales darán tres orbitales moleculares. El\(2s\) orbital no tendrá interacciones fuertes con los otros orbitales de\(A_1\) simetría debido a la gran diferencia de energía. El\(2p_z\) orbital no tendrá buena superposición con las funciones de onda para los tres orbitales de hidrógeno debido a sus posiciones en el espacio: El\(2p_z\) orbital tiene la mitad de su distribución angular apuntando lejos de los orbitales de hidrógeno, y la mitad apuntando hacia el centro de un triángulo formado por los tres átomos de hidrógeno. El nitrógeno\(2s\) y\(2p_z\) se combinarán con el hidrógeno SALC de\(A_1\) simetría para dar tres orbitales moleculares; uno orbital de enlace de baja energía, uno orbital sin enlace de energía media y un orbital antienlace de alta energía. El orbital\(a_1\) molecular sin enlace de nivel medio está cerca en energía y se asemeja al\(2p_z\) orbital de nitrógeno. El orbital\(a_1\) molecular de menor energía será menor en energía, pero será similar al nitrógeno\(2s\).
Los dos\(2p\) orbitales restantes son degenerados y poseen\(E\) simetría bajo el grupo de\(C_{3v}\) puntos. Aunque estos orbitales son una buena coincidencia de energía, nuevamente, su orientación y posiciones en el espacio no permiten una buena superposición orbital, y sus interacciones de unión y antiadhesión son relativamente débiles en comparación con lo que de otro modo podríamos esperar de una coincidencia de energía tan buena. Los orbitales\(e\) atómicos de nitrógeno se combinarán con las\(e\) SALC para dar un conjunto de dos orbitales moleculares de enlace degenerados y un conjunto de dos orbitales antiligantes degenerados (cuatro orbitales moleculares totales de\(e\) simetría). El diagrama MO para\(\ce{NH3}\) se muestra en la Figura\(\PageIndex{4}\), con las superficies de densidad de electrones calculadas de cada MO mostradas.