11.3.4: Etiquetas de simetría para términos divididos
- Page ID
- 81146
Mientras que los símbolos de términos de iones libres se derivan usando términos Russell-Saunders, solo discutimos brevemente cómo el término símbolos se pueden encontrar a partir de una tabla de caracteres al dividir el campo de ligando. Las etiquetas de simetría (llamadas Etiquetas Mulliken) que se utilizan en las tablas de caracteres para describir la simetría de las funciones de onda se describieron en una sección anterior (Sección 4.3.3). Así como los orbitales son ondulaciones que son descritas por las representaciones irreducibles que forman parte de una tabla de caracteres, también lo son los términos. Cuando estamos discutiendo los términos de un complejo octaédrico, podemos aplicar lo que ya sabemos sobre las etiquetas de simetría octaédrica y simetría para entender cómo se asignan los términos etiquetas.
Al inspeccionar de cerca cualquiera de los diagramas Tanabe-Sugano mostrados anteriormente, o en la Sección de Recursos, puede notar que cada término de iones libres (enumerados a la derecha del diagrama) se divide en un término o conjunto de términos que conservan la misma multiplicidad (el superíndice izquierdo). Bajo un campo octaédrico, todos los términos tienen símbolos\(A, B, E\) o\(T\) porque son solos, doblemente o triples degenerados. Si bien algunos de estos términos tienen subíndices “1" o “2", todos los términos también tienen subíndices\(g\)"” debido a la simetría de los\(d\) orbitales. Algunos de los símbolos también pueden parecer familiares, ya que son similares a las etiquetas que conoces para la división de\(d\) orbitales, como\(E_g\) y\(T_{2g}\).
Es útil saber que bajo un campo octaédrico, los\(D, F, G, H, I\) términos se dividen, pero los términos\(S, P\) no se dividen. A partir de la inspección de la tabla de\(O_h\) caracteres, encontramos que los términos de iones libres se dividirán de la siguiente manera:
\[\begin{array}{|l|l|} \hline \textbf{Free Ion Term} & \textbf{Terms under } O_h\\ \hline \text{S} & A_{1g} \\ P & T_{1g} \\ D & T_{2g}+E_g \\ F & A_{2g}+T_{2g}+T_{1g} \\ G & A_{1g}+E_g+T_{2g}+T_{1g} \\ H & E_g+T_{1g}+T_{1g}+T_{2g} \\ I & A_{1g}+A_{2g}+E_g+T_{1g}+T_{2g}+T_{2g} \\ \hline \end{array} \nonumber \]
El término símbolos bajo un campo octaédrico tiene simetría que coincide con la simetría de otros elementos dentro de la molécula, incluyendo los\(d\) -orbitales. A continuación se muestra un recordatorio de sus significados de simetría (véase también la Sección 4.3.3).
Cada función de onda (incluyendo términos) puede ser descrita por una etiqueta Mulliken (etiqueta de simetría). Las etiquetas utilizadas para términos en un campo de ligando octaédrico se enumeran en la siguiente tabla.
\(\begin{array}{l|l} \hline \textbf{Mulliken Labels} & \textbf{meaning}\\ \hline \text{A or B} & \text{singly degenerate} \\ E & \text{doubly degenerate} \\ T & \text{triply degenerate} \\ \hline \textbf{Subscripts} & \textbf{meaning} \\ \hline 1 & \text{symmetric to } \sigma_v \text{ or perpendicular } C_2 \\ 2 & \text{anti-symmetric to } \sigma_v \text{ or perpendicular } C_2 \\ g & \text{symmetric to inversion center} \\ u & \text{anti-symmetric to inversion center} \\ \hline \end{array} \)
Podemos usar nuestro conocimiento de simetría para derivar el término etiquetas para una configuración electrónica dada bajo un campo octaédrico. Centrémonos únicamente en la letra mayúscula que se asigna como símbolo del término. La asignación del término octaédrico no se describirá aquí, pero son similares a la asignación de estos mismos subíndices a orbitales con simetría coincidente.
Por ejemplo, la configuración de\(d^1\) electrones tiene un término de estado fundamental de iones libres de\(^2D\). De acuerdo con la tabla mostrada anteriormente, estos términos se dividirán en\(E_g\) y\(T_{2g}\) términos. ¿Cuál sería su término de estado fundamental bajo un campo octaédrico? ¿Y cuál es el término estado emocionado? Para responder a estas preguntas necesitamos observar las configuraciones de electrones de los estados terrestres y excitados en un campo octaédrico. Es conveniente saber que el término símbolo bajo un campo octaédrico indica las degeneraciones de las configuraciones de electrones relacionadas.
Echemos un vistazo a las configuraciones de electrones de los\(d\) orbitales divididos para determinar qué término es el estado fundamental. En el estado básico de un campo ligando\(d^1\) bajo un octaédrico, habría un electrón en los\(t_{2g}\) orbitales, así la configuración electrónica es\(t_{2g}^1e_g^0\). Por simplicidad solo podemos considerar los casos donde están\(m_s\) los valores\(+\frac{1}{2}\). Hay tres formas de poner el electrón\(t_{2g}\) por lo tanto, el estado fundamental es triplicamente degenerado, con un símbolo "\(T\)”. Esto se ilustra en el panel izquierdo de la Figura\(\PageIndex{1}\).
En el estado excitado de un campo ligando\(d^1\) bajo un octaédrico, habría un electrón en los\(e_{g}\) orbitales, o una configuración de\(t_2g^0e_g^1\). Hay dos formas de organizar el electrón con\(m_s=+\frac{1}{2}\) en los\(e_{g}\) orbitales (Figura\(\PageIndex{1}\), izquierda). Por lo tanto, el estado excitado es doblemente degenerado, con un símbolo "\(E\)”.
En resumen, el término de iones\(^2D\) libres para se\(d^1\) divide en un\(^2E_g\) término de menor energía\(^2T_{2g}\) y uno de mayor energía bajo un campo octaédrico (Figura\(\PageIndex{1}\), izquierda).
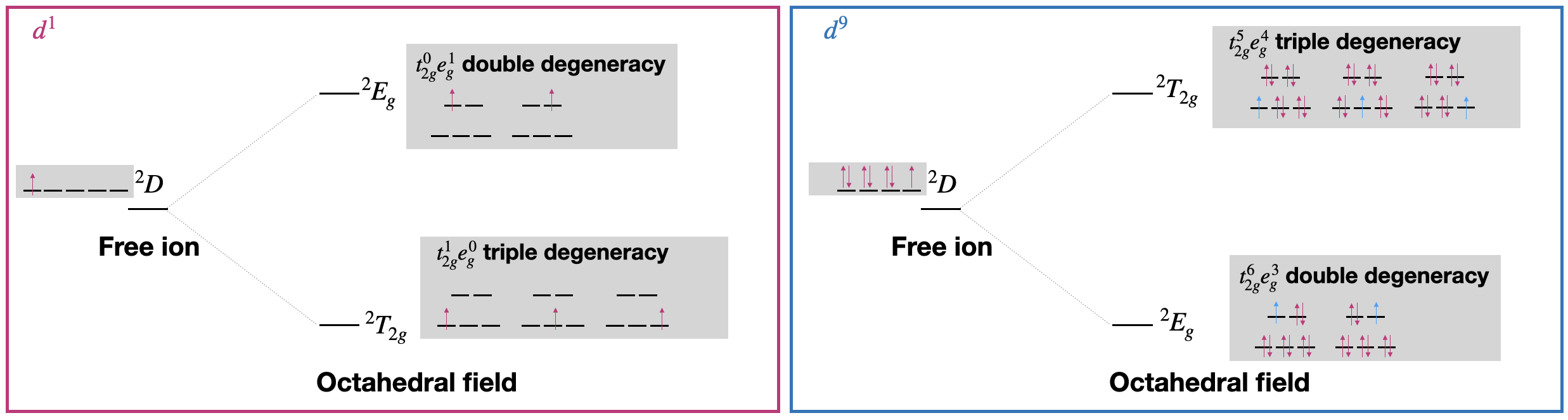
Podríamos usar un tratamiento similar para derivar las energías relativas y términos de un\(d^9\) ion en un campo octaédrico. El término estado fundamental de\(d^9\) es el mismo que para\(d^1\): es\(^2D\). Si observamos las configuraciones de electrones de estado básico y estado excitado de un\(d^9\) ion, encontramos que la configuración del estado básico es\(t_{2g}^6 e_g^3\), que es doblemente degenerada. Por otro lado, el estado excitado tiene una configuración electrónica de\(t_{2g}^5 e_g^4\), y tiene triple degeneración. En resumen, en el caso de\(d^9\), el término de iones\(^2D\) libres se divide en un\(^2E_g\) término de menor energía y un\(^2T_{2g}\) término de mayor energía. ¡Esto es exactamente lo contrario de\(d^1\)!
Los\(d^9\) casos\(d^1\) y son opuestos porque están relacionados por lo que se dice que es un concepto de “agujero positivo”. La\(d^9\) configuración podría derivarse de una\(d^{10}\) configuración con un “agujero” positivo (un electrón eliminado). El agujero positivo es similar al electrón solitario en\(d^1\) excepto que en el estado básico, el agujero está adentro\(e_g\), mientras que el electrón adentro\(d^1\) está\(t_{2g}\) adentro; así las dos situaciones son exactamente opuestas.
Así como\(d^1\) y\(d^9\) están relacionados por el concepto de agujero, así son\(d^4\) y\(d^6\). Si consideras que\(d^1\) es la adición de un electrón al\(d^0\) caso totalmente simétrico, entonces quizás puedas ver cómo\(d^6\) es similar en que es la adición de un electrón al\(d^5\) caso totalmente simétrico. Así,\(d^1\) y\(d^6\) tienen divisiones similares bajo el campo octaédrico. Del mismo modo,\(d^9\) se crea eliminando un electrón del caso totalmente simétrico de\(d^{10}\) y\(d^4\) se crea eliminando un electrón de\(d^5\). Así\(d^4\) y\(d^9\) tienen divisiones idénticas para sus términos de iones libres de estado fundamental, que en estos casos son un\(D\) término.
Debido a las relaciones entre\(d^1, d^4, d^6,\) y\(d^9\), se utiliza el mismo Diagrama Orgel para mostrar la división de términos para estos casos (Figura\(\PageIndex{2}\)). Los diagramas Orgel son otra forma más de diagramas de correlación.
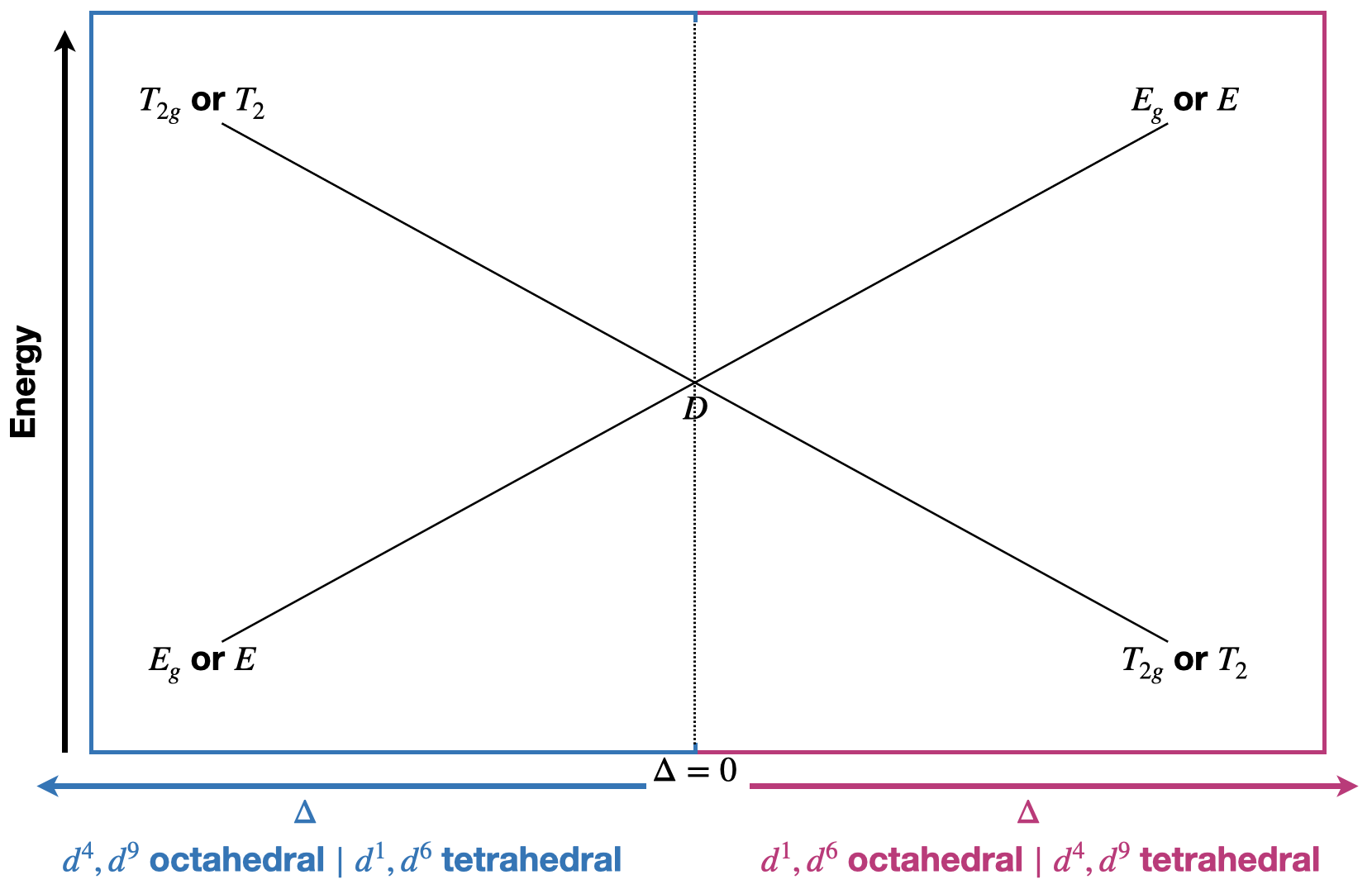
Así como hay relaciones entre\(d^1,d^4,d^6,\) y\(d^9\), hay relaciones similares entre\(d^2,d^3,d^7,\) y\(d^8\), y hay un diagrama de Orgel que puede representar la división de sus términos relevantes de iones libres.
División tetraédrica
Debido a que la división de campo tetraédrica tiene el patrón opuesto al de división octaédrica de campo de\(d\) los orbitales, existen relaciones entre términos tetraédricos y octaédricos. En general, para un campo tetraédrico con\(d^n\) electrones, se puede utilizar el diagrama Tanabe-Sugano de un diagrama octaédrico para\(d^{10-n}\) interpretar el caso tetraédrico. Los diagramas de Orgel están etiquetados en términos generales por esta razón. Se pueden aplicar tanto a casos tetraédricos como octaédricos.
Distorsiones de Jahn-Teller
También podemos ver qué pasaría con los términos en el caso de la distorsión de Jahn-Teller. En el caso de una distorsión de Jahn-Teller (más común para\(d^9\) y de espín alto\(d^4\) donde los\(e_g\) orbitales están ocupados asimétricamente), podemos usar la degeneración de configuraciones de electrones orbitales para identificar etiquetas de término. Pasemos por un ejemplo usando el caso más simple: un ion\(d^1\) metálico (Figura\(\PageIndex{3}\)).
Jahn-Teller suele provocar una distorsión tetragonal de un octaedro. Esto sería un cambio de\(O_h\) a\(D_{4h}\) simetría.
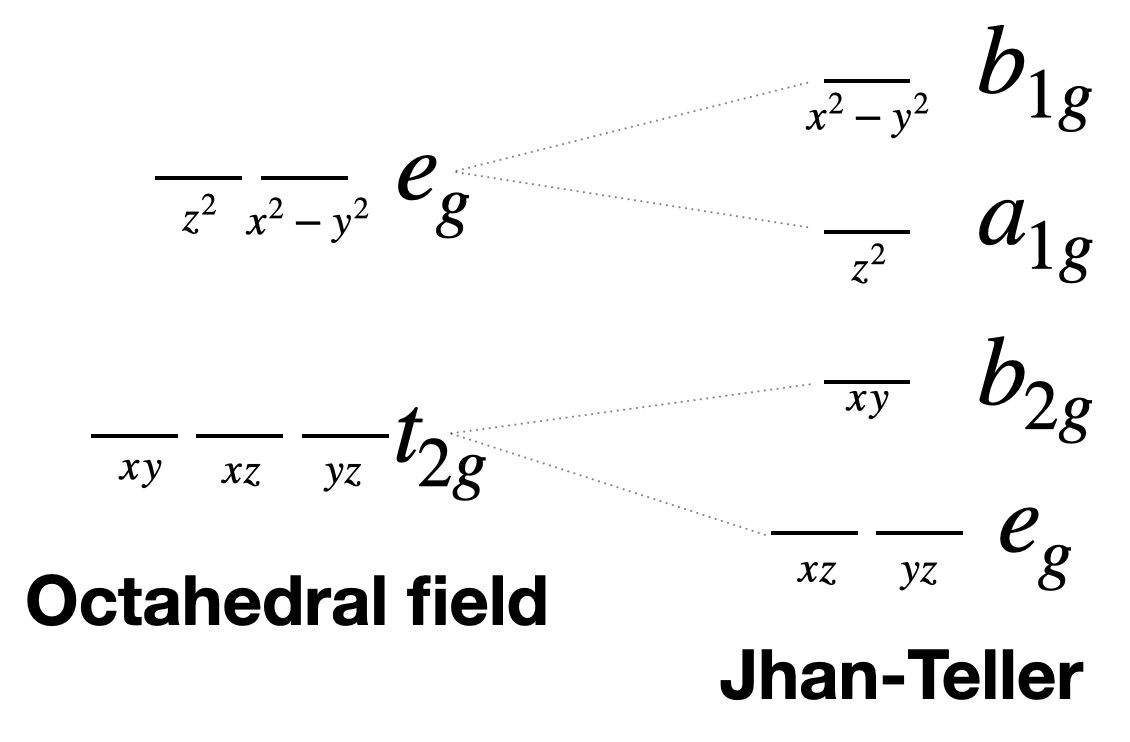
Los\(t_{2g}\) orbitales (el conjunto\(d_{xy}, d_{xz}, d_{yz}\) se dividen en\(e_g\) (\(d_{xz},d_{yz}\)) y\(b_{2g}\) (\(d_{xy}\)) por este cambio de simetría. Por lo tanto, podemos esperar que cualquier\(T_{2g}\) término se divida de manera similar en\(E_g\) y\(B_{2g}\) términos por la distorsión de Jahn-Teller. Los\(e_g\) orbitales debajo\(O_h\) se dividen en\(a_1g\) (\(d^{z^2}\)) y\(b_1g\) (\(d_{x^2-y^2}\)) debajo\(D_{4h}\). Por lo tanto, podemos esperar que\(E_g\) los términos se dividan en\(B_{1g}\) y\(A_{1g}\) términos por la distorsión de Jahn-Teller (Figura\(\PageIndex{4}\)).
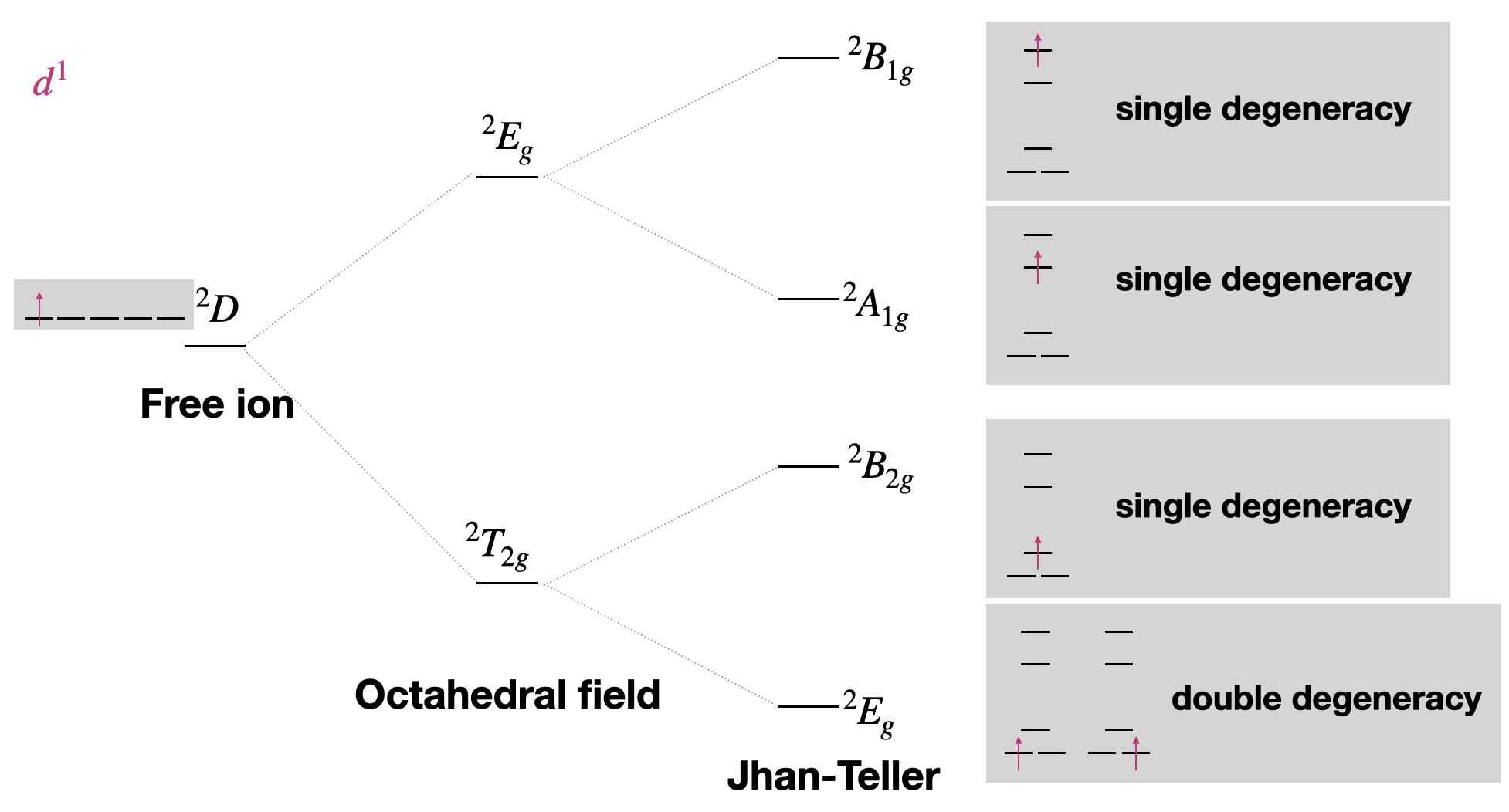
Así como\(d^1\) y\(d^9\) dieron orden opuesto de sus términos bajo un campo octaédrico, también dan orden opuesto de términos en la distorsión de Jahn-Teller.


