5.3: Números y estructuras de coordinación
- Page ID
- 70288
Números de Coordinación (CN) y Estructuras de Complejos
Los compuestos de coordinación tienen muchas estructuras o formas diferentes, y por lo tanto es importante que seamos capaces de categorizar las estructuras de los compuestos de coordinación, entender por qué se forma una estructura particular y por qué ciertas estructuras son más comunes que otras.
Un parámetro central que determina la estructura es el número de coordinación. Un número de coordinación es el número de puntos de unión entre los ligandos y el metal.
Definición: Número de Coordinación
El número de coordinación es el número de puntos de unión entre los ligandos y el metal
¿Cuáles son los principales factores que están asociados con el número de coordinación? Algunos de ellos están asociados con el ión metálico, y algunos de ellos están asociados con los ligandos. La forma y el tamaño de un ligando influye mucho en el número de coordinación. Generalmente, cuanto más voluminoso es el ligando menor que el número de coordinación. Con respecto al ion metálico, el tamaño del ion metálico juega un papel importante. Cuanto mayor es el ion metálico, más ligandos encajan alrededor de él, y el número de coordinación aumenta. Además, la configuración electrónica del ion metálico juega un papel. Para ciertas configuraciones de electrones se prefieren ciertos números de coordinación porque estos números de coordinación estabilizan las energías electrónicas. Por último, hay interacciones intermoleculares a considerar. En estado sólido ocurren entre complejos vecinos, en solución ocurren entre el complejo y las moléculas solventes. Esto puede conducir a diferentes números de coordinación y estructuras en estado sólido, y en solución, respectivamente.
Principales factores determinantes de los CNs
- Forma y tamaño de los ligandos
- Tamaño del ion metálico
- Configuración electrónica de iones metálicos
- Interacciones intermoleculares (solución vs. estado sólido)
Como puede ver, hay muchos factores que influyen en el número de coordinación, y en la forma de los complejos. Estos factores son a veces opuestos, lo que dificulta la predicción de estructuras. Sin embargo, hay una serie de reglas que permiten una precisión justa en la predicción de la estructura, y vamos a pasar por estas reglas en lo siguiente.
Números de coordinación bajos (CN)
CN = 1
La coordinación número 1 es muy rara. Cuando hay un punto de unión, generalmente hay sitios de coordinación reactivos en el ión metálico que conducen a la formación de conglomerados. Esto reduce la energía y aumenta el número de coordinación. Por ejemplo, en el metil litio (MeLi) el Li parece tener el número de coordinación 1 porque se puede pensar que solo hay un enlace Li-C único y covalente. No obstante, en realidad hay un cúmulo tetraédrico Li 4 Me 4.
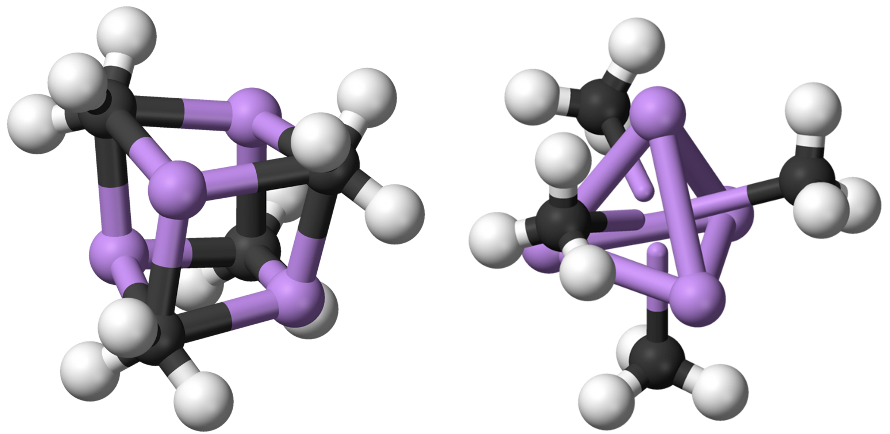
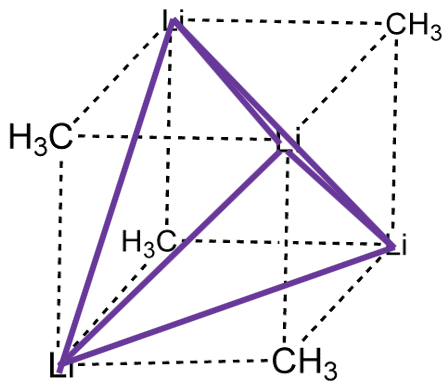
Los cuatro átomos de Li construyen un tetraedro y los grupos metilo se colocan por encima de las caras del tetraedro (Fig. 5.3.1). También se puede pensar en MeLi como una molécula casi cúbica en la que los átomos de Li ocupan cada dos vértices del cubo, y grupos metilo los vértices restantes del cubo (Fig. 5.3.2). La formación de conglomerados evita el número de coordinación 1 y estabiliza el metil litio. Además de un cúmulo tetramérico también se conoce un cúmulo hexamérico para Me-Li.
.
El número de coordinación 1 solo es posible cuando un ion metálico grande está rodeado por un ligando muy voluminoso que suprime la formación de conglomerados, y no hay coordinación de moléculas de disolvente con el metal.
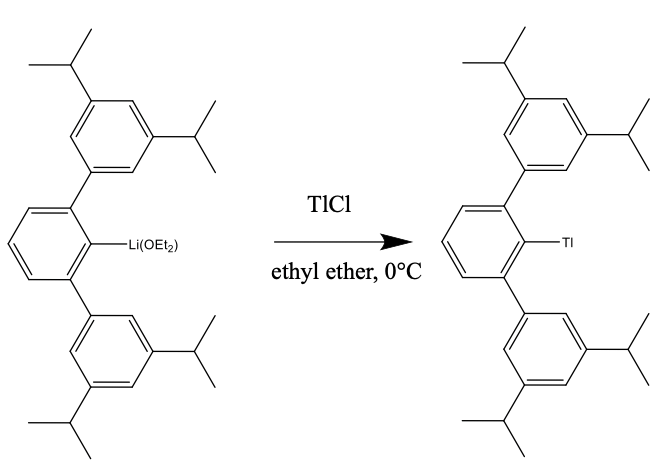
Un ejemplo el cluster 2,6, -Trip 2 C 6 H 3 Tl. (Viaje = 2,4,6, i-PR 3 C 6 H 2), Fig. 5.3.3. Tiene un Tl + coordinado a un ligando voluminoso en forma de cuenco a través de un enlace Tl-C. El Tl encaja exactamente en la cavidad en forma de cuenco en el ligando, evitando así la formación de conglomerados. El compuesto se puede preparar a partir de su derivado de litio y cloruro de talio en éter dietílico a 0°C.
CN = 2
El número de coordinación 2 también es raro, pero ya es mucho más común que el número de coordinación 1. Generalmente, los iones metálicos d 10 tienen tendencia a hacer estructuras con CN=2. Estas estructuras son estructuras lineales. Un ejemplo de un ion d 10 es Ag +. ¿Por qué es d 10? Ag se encuentra en el grupo 11, por lo que tiene 11 electrones de valencia. Si quitamos uno, hay diez. La energía del ion Ag + se minimiza cuando la subcapa 4D está llena y la subcapa 5s-está vacía. Ag + hace muchas estructuras lineales con ligandos, por ejemplo ligandos de amina o ligandos ciano. En una imagen sobresimplificada, podemos explicar la estructura usando argumentos VSEPR asumiendo que hay una hibridación sp del orbital 5s y un 5p, y los dos pares solitarios de electrones en los dos ligandos se donan a los orbitales hibridados sp. ¿Qué otros iones d 10 se te ocurren? Estaría el homólogo superior e inferior del ion Ag +, el Cu + y el ion Au +.
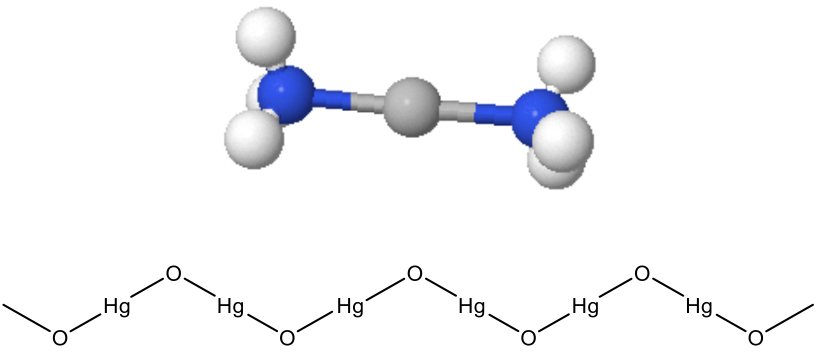
Hacen complejos lineales como CuCl 2 - y Au (CN) 2 -. Hg 2 + es también un ion d 10 que a menudo produce complejos lineales, por ejemplo Hg (CN) 2 -. Esta coordinación lineal no solo se encuentra en compuestos moleculares sino también en sólidos extendidos. Por ejemplo, HgO y HgS hacen cadenas en zig-zag de Hg 2 + coordinadas linealmente (Fig. 5.3.4). La flexión de la cadena ocurre en los aniones óxido, debido a los pares solitarios de electrones en O. Otros iones metálicos pero los iones d 10 hacen estructuras lineales solo cuando los ligandos son muy voluminosos. Estos ejemplos son raros.
CN = 3
El número de coordinación 3 también es raro para los compuestos de coordinación. Son más comunes para los iones d 10, especialmente cuando los ligandos son voluminosos. En la mayoría de los casos se adopta la estructura plana trigonal, o una estructura cercana a esa.
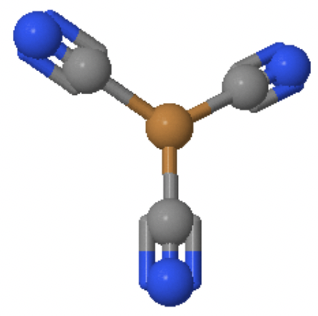
Un ejemplo es el anión Cu (CN) 3 2- en el que Cu + está rodeado por tres aniones cianuro de manera plana trigonal (Fig. 5.3.5).
CN = 4
El número de coordinación 4 es un número de coordinación muy común. En realidad es el segundo número de coordinación más común, sólo superado por el número de coordinación 6. La estructura con mucho más común asociada con el número de coordinación 4 es la estructura tetraédrica. ¿Por qué? Es porque los ligandos tienen la mayor distancia entre sí, y la menor repulsión estérica. Generalmente, los iones más pequeños y/o ligandos más grandes favorecen el número de coordinación 4 sobre el número de coordinación 6.
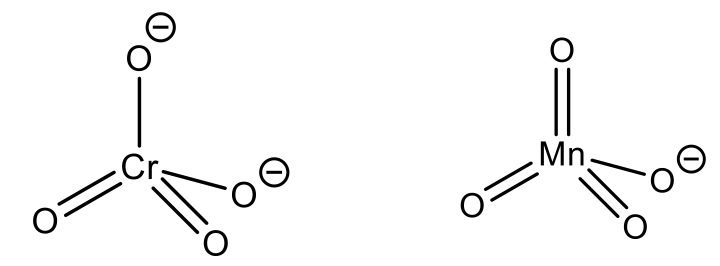
Este es el caso en el anión permanganato y el anión cromato, por ejemplo. Aquí, los estados de oxidación de Mn y Cr son +7 y +6 respectivamente, haciendo que el radio iónico sea muy pequeño.

Otro ejemplo es el ion tetrakis (piridil) cobre (1+). Aquí, los ligandos son bastante voluminosos. La estructura tetraédrica es particularmente común para los iones d 0 y d 10, y en su mayoría favorecida sobre la estructura octaédrica. Todos los ejemplos anteriores tienen ya sea d 0 o d 10 iones. Cr (VI) y Mn (VII) son d 0 y Cu (I) es d 10 cumpliendo así este requisito también.
La segunda estructura más común después de la estructura tetraédrica es la estructura plana cuadrada. Solo es común para iones con configuración de electrones d 8. ¿Qué son los iones d 8 comunes? Ejemplos son los iones Ni 2 +, Pd 2+ y Pt 2 +. Podemos encontrar estos elementos en el grupo 10 de la tabla periódica. Por lo tanto, deben tener diez electrones de valencia en estado neutro. Debido a la carga 2+, se eliminan dos electrones dejando ocho electrones. Los ocho electrones están en la subcapa de valencia d, por lo tanto, los iones se denominan iones d 8.
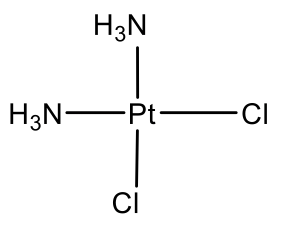
El complejo plano cuadrado más conocido es cis-platino. Tiene dos ligandos de cloro y dos de amina unidos a Pt en posición cis. Se le conoce como medicamento anticancerígeno.
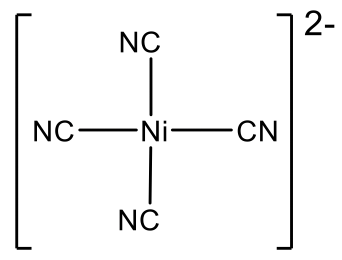
Ni (CN) 4 2- es otro ejemplo de un complejo plano cuadrado del grupo 10.
¿Se te ocurre otros iones d 8? El grupo 11 elementos Cu, Ag y Au tienen once electrones de valencia en estado neutro. En este caso necesitamos eliminar tres electrones para llegar a ocho electrones, lo que significa que Cu 3+, Ag 3 + y Au 3 + son iones d 8. Cu y Ag no son muy estables en el estado de oxidación +3, por lo que los ejemplos de cepilladora cuadrada Cu (III) y Ag (III) son bastante raros.
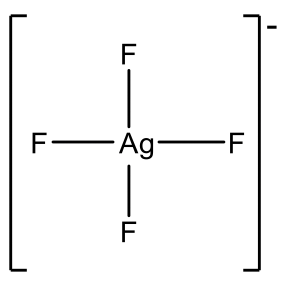
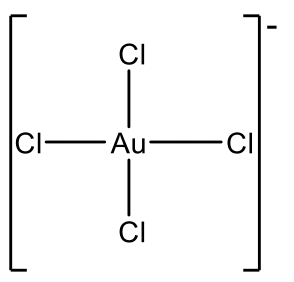
Ejemplos son AgF 4 - y CuF 4 -, Fig. 5.3.10. Sin embargo Au 3 + es más común y hay un número relativamente grande de complejos de Au (III), por ejemplo AUCl 4 -.
Debido a que los elementos del grupo 12 no son estables en el estado de oxidación 4, no hay iones del grupo 12 d 8. Sin embargo, se conocen iones del grupo 9 d 8. En este caso los iones deben estar en el estado de oxidación +1 para tener ocho d electrones. El cobalto no es estable en el estado de oxidación +1, pero Rh e Ir lo son, y los complejos planos cuadrados Rh (I) e Ir (I) son comunes.
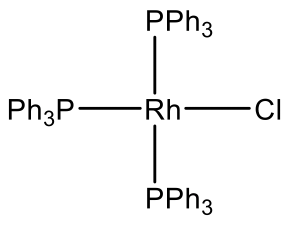
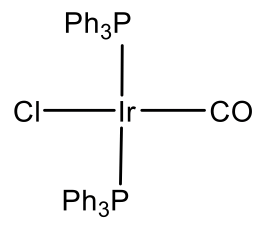
Por ejemplo Rh hace un complejo Rh (PPh 3) 3 Cl (Fig. 5.3.11). Es un catalizador de hidrogenación común. El complejo de Vasca Ir (CO) (PPh 3) 2 Cl es otro ejemplo (Fig. 5.3.11). Tiene la propiedad de unir oxígeno de manera reversible.
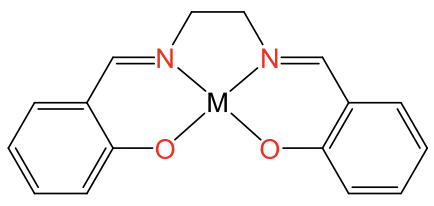
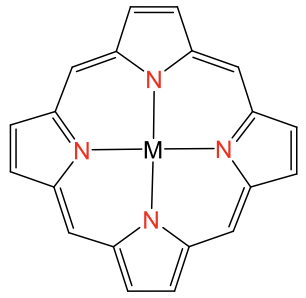
La coordinación plana cuadrada es posible también con iones metálicos distintos de los iones d 8, pero solo cuando el ligando fuerza al ion metálico a esta coordinación. Los ligandos que hacen esto son, por ejemplo, el ligando de porfirina y el ligando salen. Son ligandos tetradentados con átomos donantes que forman un cuadrado obligando al ion metálico a adoptar una coordinación cuadrado-plana (Fig. 5.3.12).
Una última posibilidad es la estructura del balín. Es conocido por elementos de grupo principal, pero no para elementos de metal de transición.
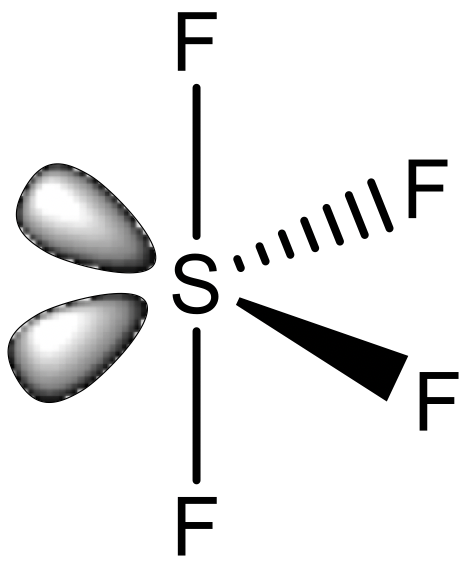
Un ejemplo es SF 4 (Fig. 5.3.13). La estructura del balancín se deriva de la estructura octaédrica mediante la cual dos esquinas adyacentes del octaedro están ocupadas por pares solitarios de electrones. Formalmente se podría considerar un compuesto como SF 4 como un compuesto de coordinación en el que cuatro ligandos F - se unen a un catión S 4+. Sin embargo, esta visión comúnmente no se adopta, y los enlaces S-F no se ven como enlaces covalentes dativos.
CN = 5
Para la coordinación número 5, las dos estructuras más comunes son la bipirámide trigonal y la pirámide cuadrada. Son casi igualmente comunes porque tienen energías muy similares. Cuál es el preferido, depende de las circunstancias particulares, la naturaleza del metal, los ligandos, el disolvente, etc. Muchas moléculas tienen estructuras en el medio, en su mayoría descritas como bipirámides trigonales distorsionadas. La distorsión es aún más común en estado sólido debido a los efectos de empaque. Los efectos de empaque minimizan el espacio vacío en el cristal.
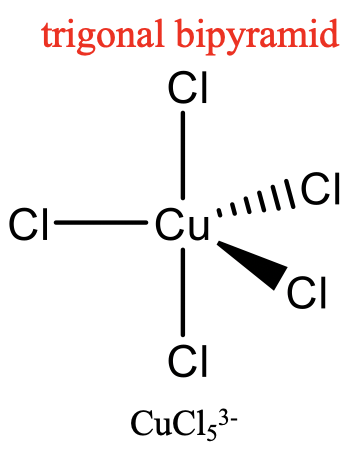
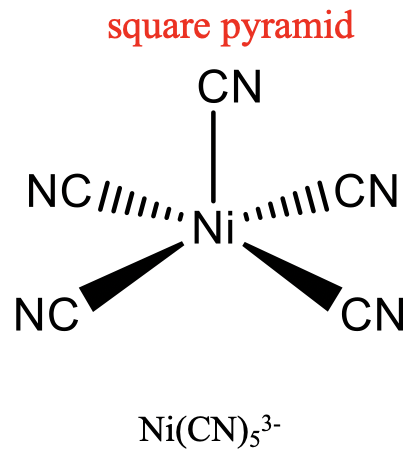
Un ejemplo para una estructura bipiramidal trigonal es CuCl 5 3-, un ejemplo para una estructura piramidal cuadrada es Ni (CN) 5 3- (Fig. 5.3.14). Se desconoce el pentágono, otra estructura concebible. Los compuestos de cinco coordenadas son conocidos por toda la gama de metales de transición. Una diferencia respecto a las estructuras con los números de coordinación 2 a 4 es, que en las estructuras con el número de coordinación 5 no todos los ligandos son equivalentes a simetría. Para la forma bipiramidal trigonal distinguimos entre ligandos axiales y ecuatoriales. En los complejos piramidales cuadrados, el quinto ligando en la punta de la pirámide es simétricamente diferente a los otros cuatro en la base de la pirámide.
Debido a que la diferencia de energía entre la estructura bipiramidal trigonal y la estructura piramidal cuadrada es pequeña, y solo hay una pequeña barrera de activación entre las dos estructuras, a menudo son fluxionales. Esto significa que pueden interconvertir dinámicamente.
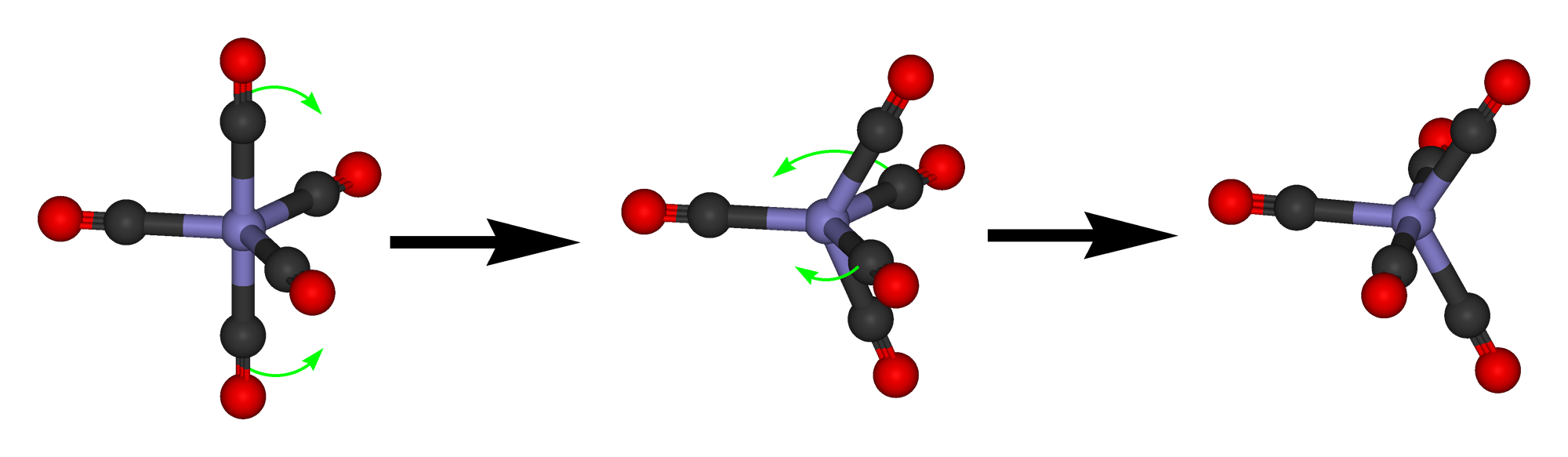
Esta interconversión se produce de acuerdo con un mecanismo llamado pseudo rotación de Berry. En la pseudo-rotación de Berry un ángulo de unión de 120° entre dos ligandos en posición ecuatorial aumenta hasta que finalmente es 180°. El ángulo inicial de 180° entre dos ligandos en posición axial disminuye hasta llegar a 120°. Esto significa que los dos ligandos anteriormente ecuatoriales son ahora ligandos axiales, y los dos ligandos axiales son ahora ligandos ecuatoriales. A medida que ocurren las pseudo rotaciones de Berry, el complejo se mueve de una estructura bipiramidal trigonal a través de un intermedio piramidal cuadrado a otra estructura bipiramidal trigonal. La pseudo rotación de Berry ocurre a menudo muy rápido, por lo tanto en muchas mediciones los cinco ligandos parecen idénticos. Por ejemplo, la molécula PF 5 muestra solo una señal en el 19 F NMR debido a que el movimiento de los átomos F desde la posición ecuatorial a la axial y viceversa es demasiado rápido para la escala de tiempo de RMN. A bajas temperaturas, la pseudo rotación de Berry puede ser lo suficientemente lenta para que las posiciones axiales y ecuatoriales puedan resolverse. En compuestos con ligandos más grandes la pseudorotación también puede ser lo suficientemente lenta para que las posiciones axiales y ecuatoriales se resuelvan en la RMN.
CN = 6
El número de coordinación más común es el número de coordinación 6. Este número de coordinación existe para todas las configuraciones de electrones de metales de transición de d 0 a d 10. Esto lo podemos explicar por el hecho de que muchos iones metálicos tienen el tamaño adecuado para soportar seis ligandos a su alrededor, y hay muchos ligandos que tienen el tamaño adecuado para rodear a un ion metálico en el número de coordinación 6. La forma con mucho más común para el número de coordinación 6 es la forma octaédrica. Es la forma para la que los ligandos tienen la mayor distancia entre sí minimizando así la repulsión estérica. Una segunda razón es que la orientación de los orbitales atómicos soporta la forma octaédrica, ya que muchos orbitales apuntan a lo largo de los ejes x, y, y z, en particular los orbitales p, y los d z 2 así como los d x 2 -y 2.
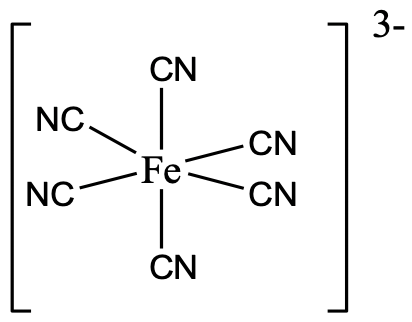
Un ejemplo es el anión hexacyanoferrato (3-) en el que seis ligandos ciano rodean el ión metálico octaédricamente (Fig. 5.3.16).
Distorsiones de Complejos con CN = 6
Los complejos octaédricos pueden distorsionarse de dos maneras básicas. La primera distorsión común es la denominada distorsión tetragonal. La distorsión tetragonal se puede lograr ya sea alargando un octaedro a lo largo de dos vértices opuestos, o comprimiendo el octaedro a lo largo de dos vértices opuestos.
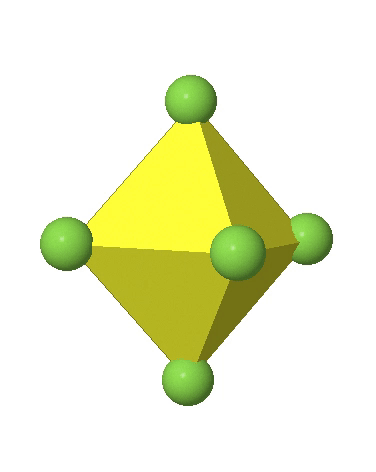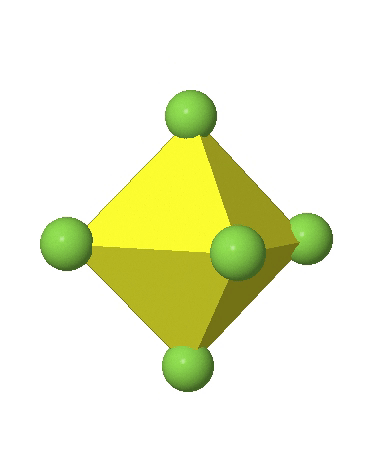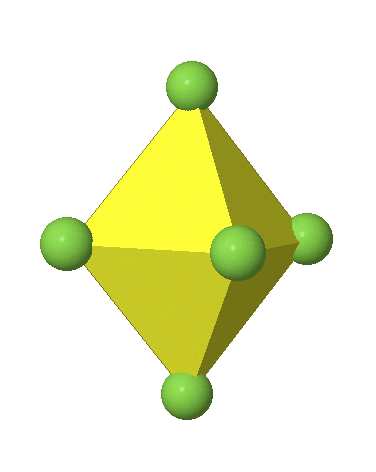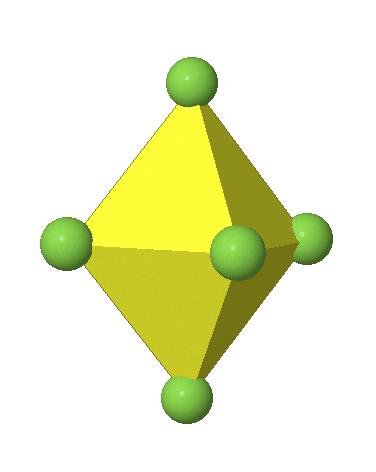
En el primer caso, dos vértices opuestos están más alejados del centro del octaedro en comparación con las otras cuatro esquinas (Fig. 5.3.17).
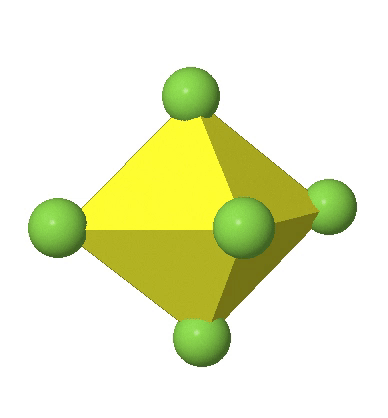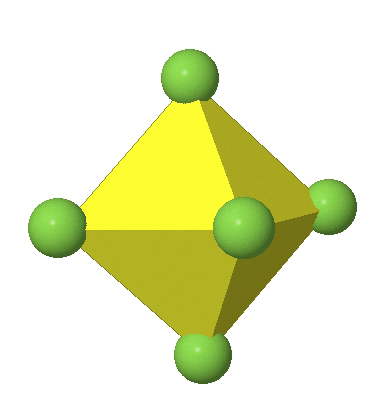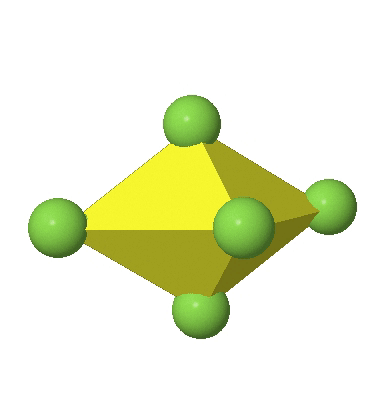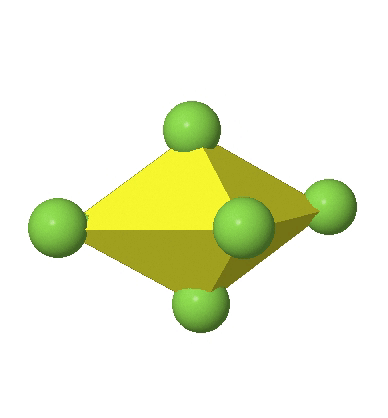
En el octaedro comprimido dos esquinas opuestas están más cerca del centro en comparación con las otras cuatro esquinas (Fig. 5.3.18). Tanto el octaedro alargado como el comprimido tienen la misma simetría, es decir, pertenecen al mismo grupo de puntos. ¿Qué grupo de puntos es? Todavía tenemos un eje principal C 4, pero solo uno. Pasa por las esquinas de los dos vértices opuestos a lo largo de los cuales nos distorsionamos. Hay un plano de espejo horizontal perpendicular al eje C 4, así como un centro de inversión. Así, el grupo de puntos debe ser D 4h. En octaedros tetragonalmente distorsionados todas las caras son equivalentes, pero las distancias de los ligandos desde el centro del octaedro no son las mismas.
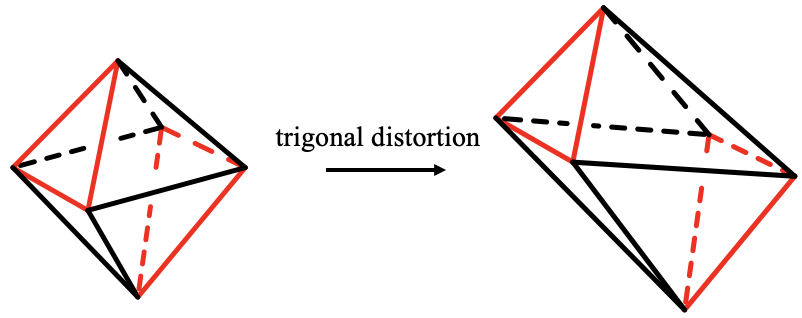
Cuando alargas o comprimes el octaedro a lo largo de caras opuestas creas un antiprisma trigonal (5.3.19). Se llama antiprisma porque las dos caras triangulares regulares opuestas, mostradas aquí en rojo, están orientadas de manera escalonada. Este tipo de distorsión se llama distorsión trigonal. El grupo puntual de un antiprisma trigonal es D 3d. El eje C 3 atraviesa las dos caras triangulares regulares opuestas del antiprisma. Hay tres ejes C 2 de pie perpendiculares, y pasando por los centros de las seis caras triangulares distorsionadas restantes. También hay tres planos de espejo verticales que bisecan el ángulo entre los ejes C 2. En un antiprisma trigonal las caras no son todas iguales, pero la distancia de los vértices son todas iguales.
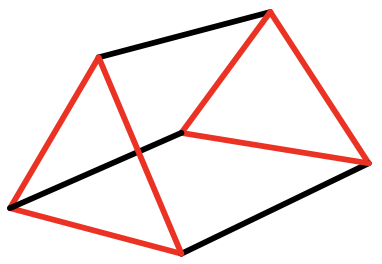
Cuando giramos 60° una de las dos caras triangulares opuestas de un antiprisma, las dos caras quedan eclipsadas y resulta un prisma trigonal (Fig. 5.3.20). Los compuestos prismáticos trigonales se observan principalmente cuando hay tres ligandos bidentados que conectan las caras triangulares superior e inferior. ¿Cuál es el grupo de puntos? Es D 3h. Hay un C 3 ejes pasando por los dos triángulos opuestos. 3 C 2 ejes van por los centros de los tres rectángulos, y hay un plano espejo horizontal perpendicular al eje C 3. ¿Un alargamiento o compresión a lo largo de las dos caras triangulares opuestas cambia la simetría? Piénsalo. No, no lo cambia.
CN = 7
Los números de coordinación superiores a 6 se consideran números de coordinación altos. Son significativamente menos comunes que los números de coordinación, 4, 5 y 6. Una explicación simple es que los grandes números de coordinación requieren un catión muy grande o un anión muy pequeño de la combinación de ambos para evitar la repulsión estérica. Estas condiciones son estadísticamente menos probables. Además, los grandes números de coordinación no son tan favorables desde el punto de vista de la orientación orbital.
Veamos primero la coordinación número 7 con más detalle. Hay tres estructuras posibles que son casi igualmente comunes en la naturaleza.
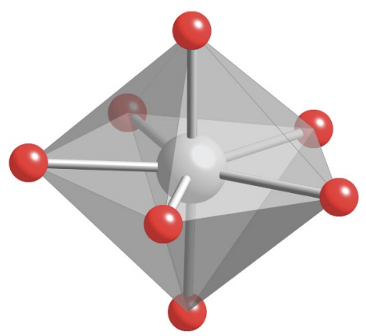
El primero es la bipirámide pentagonal de la cual ZrF 7 3- es un ejemplo (Fig. 5.3.21).
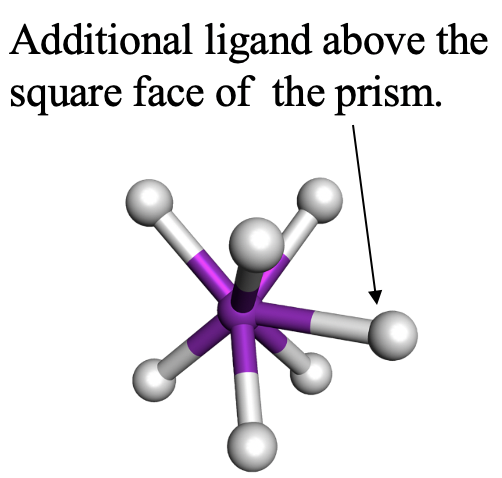
El segundo es el prisma trigonal tapado. TaF 7 2- es un ejemplo para ello (Fig. 5.3.22). El séptimo ligando se coloca sobre una cara cuadrada del prisma, no una cara triangular. ¿Te imaginas por qué? Piénsalo un momento. La respuesta es que la cara cuadrada es más grande que la cara triangular, y por lo tanto hay menos repulsión estérica.
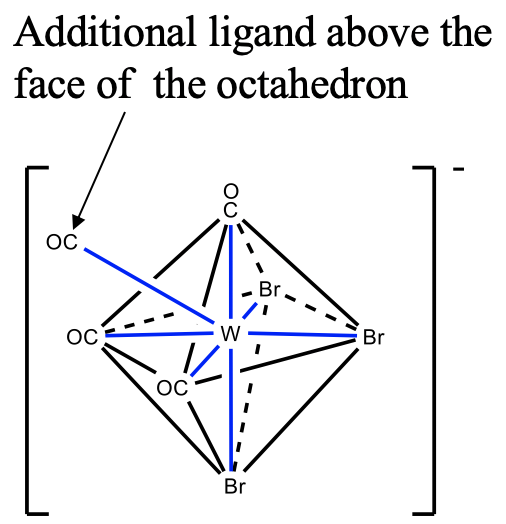
La tercera estructura es el octaedro tapado. Un ejemplo es el tribromotetracarboniltungstato (IV). En este compuesto tres ligandos bromo y tres ligandos carbonilo ocupan los vértices de dos caras opuestas en el octaedro. El cuarto ligando carbonilo se coloca por encima de la cara triangular con los ligandos carbonilo. Se puede ver que al igual que para la coordinación número 5, los ligandos no son simétricamente equivalentes.
CN = 8
Ahora, vayamos a la coordinación número 8. ¿Qué formas te imaginas que adoptan la coordinación número 8? La forma más simétrica y simple es el cubo (Fig. 5.3.24).

Figura 5.3.24 Transformación de un cubo en antiprisma cuadrado. No se conocen complejos cúbicos.
Sin embargo, no se observan complejos con formas cúbicas. Esto se debe a que existe otra estructura relacionada que es energéticamente más favorable. Es el antiprisma cuadrado (Fig.5.3.25). En un antiprisma cuadrado, dos caras cuadradas opuestas están orientadas de manera escalonada una respecto a la otra. En relación con el cubo, una cara del cubo gira 45° con respecto a la cara opuesta, y las dos caras cuadradas opuestas están interconectadas entre sí para formar caras triangulares. Se prefiere el antiprisma cuadrado sobre el prisma cuadrado porque los vértices donde se asientan los ligandos tienen una mayor distancia entre sí en comparación con el cubo.

Un ejemplo de un compuesto de coordinación que hace un antiprisma cuadrado es el anión tetraoxolato circonato (4-).
Una estructura relacionada con el antiprisma cuadrado es el dodecaedro. Tenga en cuenta que no estamos hablando del dodecaedro que aquí es un sólido platónico. Podemos derivar el dodecaedro apretando en las dos esquinas opuestas de los dos cuadrados. Esto distorsiona y dobla un cuadrado para formar dos caras triangulares adicionales. Esto produce el dodecaedro (Fig. 5.3.26).
Se puede acceder a un video de la transformación de antiprisma cuadrado a dodecaedro a través del siguiente enlace:
https://www.youtube.com/watch?v=A8G7...ature=youtu.be

Un ejemplo de esta forma es el octacyanomolibdato complejo (3-), (Fig. 5.3.26). Como se puede ver en los ejemplos, todos los iones metálicos son iones metálicos grandes, y los ligandos un pequeño, confirmando que las estructuras con grandes números de coordinación se ven favorecidas por iones metálicos grandes y pequeños ligandos.
CN = 9
Por último, pensemos en formas asociadas a la coordinación número 9.
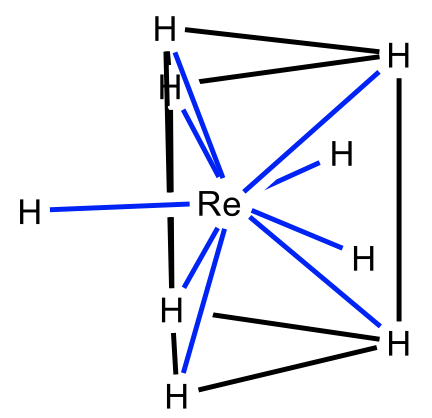
Una forma posible es el prisma trigonal tritapado para el cual el nonahidridorhenato es un ejemplo (Fig. 5.3.27). Aquí se colocan tres ligandos adicionales por encima de las tres caras rectangulares del prisma trigonal. Como era de sorprender, los ligandos son pequeños y el ion metálico es grande.
Otro ejemplo es el antiprisma tricapado. El catión nonaammine lantano (3+) es un ejemplo. En este caso los tres ligandos adicionales se colocan por encima de tres caras triangulares de un antiprisma. El número de coordinación 9 no es el límite superior para los números de coordinación. Se han observado números de coordinación hasta 16, pero son raros.


