1.7: Mediciones de densidad y gravedad específica
- Page ID
- 77211
Densidad
La densidad es la relación masa-volumen de una sustancia.
La densidad es una característica física de la materia. Cada sustancia tiene una densidad característica que puede ser utilizada como un indicio para identificar una sustancia.
Los gases tienen una densidad muy baja, generalmente expresada en g/L, por ejemplo, la densidad del aire es de alrededor de 1.224 g/L a nivel del mar y 15 o C. La densidad de líquidos y sólidos suele expresarse en g/mL. Por ejemplo, la densidad del agua a 4 o C es de 1.00 g/mL.
Los objetos que son menos densos que el agua flotan, y los objetos más densos que el agua se hunden en el agua. Por ejemplo, el petróleo es menos denso que el agua y flota sobre el agua. Los metales son más densos que el agua y se hunden en el agua. La densidad de algunas sustancias comunes se enumera en la Tabla 1
|
Sustancia |
Densidad (g/mL) |
|---|---|
|
hidrógeno |
0.000089 |
|
dióxido de carbono |
0.0019 |
|
alcohol etílico |
0.7893 |
|
agua |
1.00 |
|
magnesio |
1.74 |
|
sal de mesa |
2.16 |
|
aluminio |
2.70 |
|
hierro |
7.86 |
|
cobre |
8.92 |
|
plata |
10.50 |
|
plomo |
11.34 |
|
mercurio |
13.59 |
|
oro |
19.30 |
Medición de densidad
La densidad (d) se calcula a partir de la masa (m) y el volumen (V) de una sustancia mediante la fórmula:
\[d = \frac{m}{V}\nonumber\]
La masa generalmente se mide usando una balanza analítica. El volumen de líquidos se puede medir usando un cilindro graduado, pipeta o botella de densidad. El volumen de sólidos regulares se puede calcular a partir de los parámetros geométricos. Por ejemplo, el volumen de un rectángulo es igual a largo x ancho x alto. El volumen de un cubo es igual a la longitud del borde en cubos.
El volumen de una forma irregular que se vende generalmente se mide debido a que las sustancias que son más densas que el agua se hunden y desplazan una cantidad igual de agua. La figura 1.7.1 ilustra la medición de densidad de un objeto sólido de forma irregular que se hunde en el agua, como se explica en el siguiente ejemplo.

¿Cuál es la densidad del objeto en la Fig. 1.7.1?
Soution
la masa (m) del objeto en balance es de 1000.00 g. El volumen del objeto es igual al volumen del agua desplazada por el objeto, que es de 225.0 mL — 100.0 mL = 125.0 mL.
\ begin {ecuación}
d=\ frac {m} {V} =\ frac {1000.00\ mathrm {~g}} {125.0\ mathrm {~mL}} =8.000\ frac {\ mathrm {g}} {\ mathrm {ml}}\ nonumber
\ end {ecuación}
La mayoría de las veces, las calculadoras dan números más significativos y a veces menos de lo necesario; ambas necesitan corrección. En el ejemplo 1.7.1, la calculadora muestra 8, es decir, una cifra significativa, pero se agregan tres ceros para hacer cuatro cifras significativas.
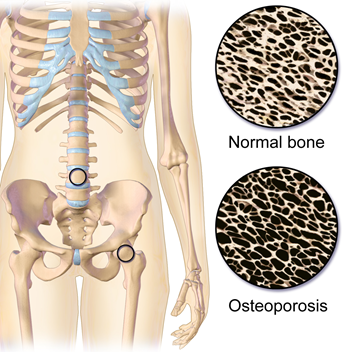
Densidad ósea y osteoporosis
La osteoporosis es una enfermedad ósea asociada a una disminución de la densidad ósea, particularmente en adultos mayores. Los huesos siempre pierden y ganan calcio, magnesio y fosfato. En la infancia, los huesos se construyen más rápido que la descomposición, pero en la vejez, el proceso se invierte, y los huesos comienzan a adelgazarse, se vuelven más fuertes y se vuelven más propensos a la fractura, como se ilustra en la Fig. 1.7.2. Los cambios hormonales, las enfermedades y algunos medicamentos contribuyen al adelgazamiento óseo. La pérdida severa de densidad ósea se llama osteoporosis.
Gravedad específica
La gravedad específica es la relación entre la densidad del objeto y la densidad del agua, es decir:
\ begin {ecuación}
\ text {Gravedad específica} =\ frac {\ text {Densidad de un objeto}} {\ text {Densidad del agua}}\ nonumber
\ end {ecuación}
La gravedad específica es la relación entre la densidad del objeto y la densidad del agua, es decir:
\ begin {ecuación}
\ text {Gravedad específica} =\ frac {\ text {Densidad de un objeto}} {\ text {Densidad del agua}}\ nonumber
\ end {ecuación}
Las unidades cancelan en la proporción. Por lo tanto, la gravedad específica es un número sin unidad. La densidad del agua es de 1.0 g/mL a temperatura ambiente, por lo que la gravedad específica es igual a la densidad del objeto expresada sin una unidad.
Cuando las sustancias se disuelven en agua, la densidad de la solución suele ser diferente de la del agua pura. Por ejemplo, la densidad de sangre completa para los humanos es de ~1.060 g/mL. La densidad de orina varía en el rango de 1.0050 g/mL a 1.030 g/mL. Tanto la sangre como la orina tienen sustancias disueltas en el agua que aumentan la densidad de la del agua pura. Tanto alta como baja densidad o gravedad específica que el rango normal de orina indica problemas médicos. Un aumento en la gravedad específica de la orina indica que se debe a un aumento en los solutos causados por deshidratación, diarrea o infección. De igual manera, una disminución en la concentración de soluto disminuye la gravedad específica de la orina, lo que indica problemas médicos como insuficiencia renal.
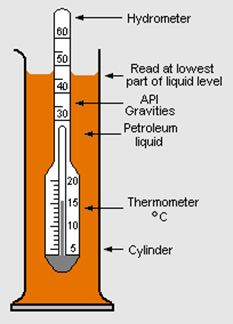
Medición de gravedad específica
La gravedad específica generalmente se mide usando un instrumento llamado hidrómetro. El hidrómetro se sumerge parcialmente en la muestra líquida, y se registra la lectura en la escala en el punto de unión aire-agua, como se ilustra en la Fig. 1.7.3.