1.6: Ecuaciones y gráficas
( \newcommand{\kernel}{\mathrm{null}\,}\)
Las igualdades donde ambos lados tienen un solo término, es decir, monomio, conducen a los factores de conversión. Si uno o ambos lados de la igualdad tienen más de un término, es decir, polinomio, lleva a una fórmula que hace el mismo trabajo, es decir, convertir unidades. Las ecuaciones de conversión de temperatura y las ecuaciones de gases ideales y el procedimiento de manipulación de estas ecuaciones se describen a continuación como ejemplos de cómo manipular las preguntas necesarias para realizar cálculos.
Ecuaciones de conversión de temperatura
Existen tres escalas de temperatura de uso común: Celsius (o C), Kelvin (K) y Fahrenheit (o F), ilustradas en la Fig. 1.6.1.
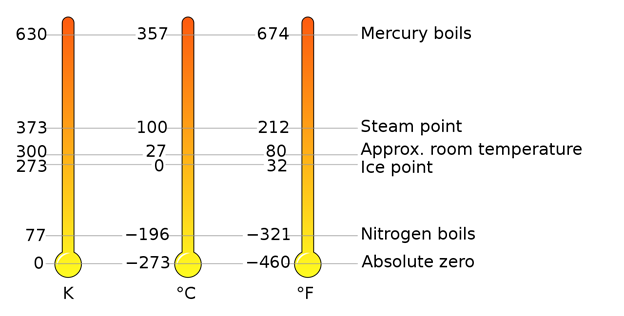
Celsius (o C)
La escala Celsius tiene O o C en el punto de congelación del agua y 100 o C en el punto de ebullición del agua. Celsius es la unidad base de temperatura en el sistema métrico.
La escala Kelvin
Kelvin es la unidad base de temperatura en el SI. El punto de congelación del agua es 273.15 K, y el punto de ebullición del agua es 373.15 K. Para fines más prácticos, el punto de congelación del agua se reporta como 273 K y el punto de ebullición 373 K, es decir, exacto a tres cifras significativas. Las unidades de escala Celsius son del mismo tamaño pero cambiadas 273 en comparación con la escala Kelvin. Entonces, la relación entre Kelvin y Celsius es:
\ begin {ecuación}
T_ {K} = T_ {C} +273,\ nonumber
\ end {ecuación}
donde T K es la temperatura en Kelvin, y T C es la temperatura en grados Celsius. Esta ecuación convierte la temperatura en Kelvin en temperatura en Celsius.
A 0 K, también llamado cero absoluto, es la temperatura de una materia a la que no se puede eliminar energía como calor de la materia. No hay temperatura negativa en la escala Kelvin.
Fahrenheit (o F)
Fahrenheit es la unidad base del sistema inglés, con 32 o F en el punto de congelación del agua y 212 o F en el punto de ebullición del agua. Fahrenheit es59 veces más corto y se desplaza hacia arriba en 32 grados que Celsius. Entonces la relación entre ambos es:
\ begin {ecuación}
T_ {F} =\ frac {9} {5}\ veces T_ {C} +32,\ nonumber
\ end {ecuación}
donde T F es la temperatura en Fahrenheit, y T C es la temperatura en grados Celsius. Esta ecuación convierte la temperatura en Celsius a temperatura en Fahrenheit.
Manipulación de ecuaciones de conversión de temperatura
La ecuación para convertir Celsius a Fahrenheit es:
\ begin {ecuación}
T_ {F} =\ frac {9} {5}\ veces T_ {C} +32,\ nonumber
\ end {ecuación}
La suma o resta del mismo número en los dos lados de una ecuación no cambia la igualdad. Restar 32 de ambos lados de la ecuación anterior conduce a:
\ begin {ecuación}
T_ {F} -32=\ frac {9} {5}\ veces T_ {C}\ cancel {+32}\ cancel {-32},\ nonumber
\ end {ecuación}
\ begin {ecuación}
T_ {F} -32=\ frac {9} {5}\ veces T_ {C}. \ nonumber
\ end {ecuación}
La multiplicación o división por el mismo número en ambos lados de una ecuación no cambia la igualdad. Recuerda que la multiplicación o división debe aplicarse a cada término a cada lado de la igualdad. Encerrar el lado con más de un término entre corchetes pequeños y luego hacer la multiplicación de la operación de división para que aplique a cada término en el paréntesis. Multiplicar ambos lados de la ecuación anterior con59 conduce a:
\ begin {ecuación}
\ frac {5} {9}\ veces\ izquierda (T_ {F} -32\ derecha) =\ cancel {\ frac {5} {9}}\ veces\ cancel {\ frac {9} {5}}\ veces T_ {C}\ nonumber
\ end {ecuación}
\ begin {ecuación}
\ frac {5} {9}\ veces\ izquierda (T_ {F} -32\ derecha) =T_ {C}\ nonumber
\ end {ecuación}
Cambiar los lados de una ecuación no cambia la igualdad. Intercambiando los lados en la ecuación anterior para llevar T C a la izquierda:
\ begin {ecuación}
T_ {C} =\ frac {5} {9}\ veces\ izquierda (T_ {F} -32\ derecha)\ nonumber
\ end {ecuación}
Esta es la ecuación para la conversión de Fahrenheit a Celsius.
El procedimiento de reorganización de una ecuación descrita anteriormente se aplica a todas las ecuaciones algebraicas. Por ejemplo, comience con una relación que convierta Celsius a Kelvin:
\ begin {ecuación}
T_ {K} = T_ {C} +273,\ nonumber
\ end {ecuación}
restar 273 de ambos lados:
\ begin {ecuación}
T_ {K} -273= T_ {C}\ cancelar {+273}\ cancelar {-273},\ nonumber
\ end {ecuación}
\ begin {ecuación}
T_ {K} -273= T_ {C},\ nonumber
\ end {ecuación}
y finalmente intercambiar el lado izquierdo y derecho para llevar T C a la izquierda:
\ begin {ecuación}
T_ {C} =T_ {K} -273. \ nonumber
\ end {ecuación}
Esta es la ecuación para la conversión Kelvin a Celsius.
Ecuación de gas ideal
La ecuación de gas ideal relaciona más de dos variables:
PV=nRT,
donde P es presión, V es volumen, n es la cantidad de gas en moles, T es la temperatura (en K), y R es la constante de proporcionalidad llamada constante de gas ideal. Dividir ambos lados de la ecuación con V conduce a:
P×VV=nRTV,
P=nRTV.
Permite calcular la presión de una muestra de gas si se conoce la cantidad en moles, la temperatura en kelvin y el volumen de la muestra de gas, junto con el valor de la constante R en las unidades consistentes. Del mismo modo, la reorganización de la ecuación conduce a fórmulas para calcular, V, T o n de una muestra de gas:
\ begin {ecuación}
V=\ frac {n R T} {P},\ quad T=\ frac {P V} {n R},\ quad\ texto {y}\ quad n=\ frac {P V} {R T}\ nonumber
\ end {ecuación}
Gráficas
La gráfica es una presentación visual de una relación entre dos variables. La Fig. 1.6.2 muestra una gráfica que presenta una relación entre el volumen y la presión de una cantidad dada de gas a una temperatura constante, conocida como ley de Boyle.
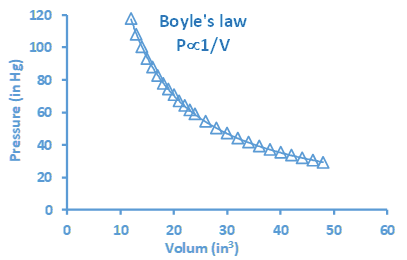
Los componentes típicos de una gráfica son los siguientes.
- Un título que diga de qué trata la gráfica, por ejemplo, “La ley de Boyle:” en la gráfica de la Fig. 1.6.2.
- Ejes: el eje x es una línea horizontal, y el eje y es una línea vertical. Los ejes suelen tener una escala distribuida uniformemente a partir de cero. El eje x representa la variable independiente, y el eje y representa la variable dependiente. Por ejemplo, el volumen es independiente, y la presión es la variable dependiente en la Fig. 1.6.2.
- Etiquetas de ejes que indican el nombre de la variable y las unidades de medida. Por ejemplo, volumen (en 3) y presión (en Hg), donde en 3 y en Hg son las unidades de las variables.
- Símbolos que representan puntos experimentales. Por ejemplo, Δsímbolos en la Fig 1.6.2, en el cruce de una línea vertical partiendo de una variable independiente de valor experimental en el eje x y una línea horizontal a partir del valor correspondiente de la variable dependiente en el eje y.
- Una curva conecta los puntos experimentales y muestra la tendencia en la relación. Por ejemplo, el curado en la Fig. 1.6.2 indica que la presión disminuye a medida que aumenta el volumen.
Interpretación de una gráfica
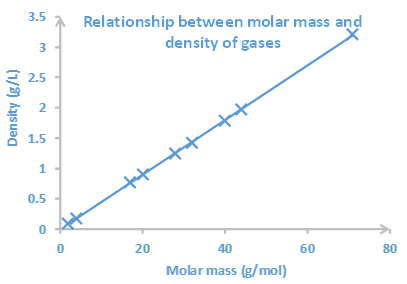
Interpretación es leer la tendencia o relación entre las variables trazadas. Por ejemplo, la Fig. 1.6.2 muestra que la presión disminuye a medida que aumenta el volumen de gas. La curva también permite leer el valor de una variable a partir del valor de la otra. Por ejemplo, si el volumen es de 30 en 3, la presión sería de ~50 en Hg. Para leer: dibuja una línea vertical a partir del valor dado en el eje x y una línea horizontal desde el punto donde la línea vertical cruza la curva. Luego, lea el valor donde la línea horizontal se encuentra con el eje y. El proceso se invierte cuando el valor dado es de la variable dependiente en el eje y, y el deseado es el valor correspondiente de la variable independiente en el eje x. Por ejemplo, si la presión es de 40 in Hg, el volumen es de aproximadamente 35 en 3. La Fig. 1.6.3 es otro ejemplo de una gráfica que muestra una relación entre la masa molar y la densidad de los gases a una temperatura constante. El curado en esta gráfica dice que la densidad de gases aumenta a medida que aumenta la masa molar.