2.3: Átomos de los elementos
- Page ID
- 77181
Símbolo de un elemento
Los elementos están representados por símbolos, el primer alfabeto de su nombre inglés o no inglés, escritos en mayúsculas. Por ejemplo, C para carbono, N para nitrógeno y I para yodo. Por lo general, otro alfabeto también se elige del nombre del elemento y se escribe como letra pequeña, por ejemplo, Al para aluminio, Zn para zinc y Ca para calcio. Algunos símbolos de elementos se derivan de nombres no ingleses, por ejemplo, Na para sodio del nombre latino natium, Cu para cobre del latín cupurum y Ag para plata del latín argentum.
Los átomos del mismo elemento tienen el mismo número de protones, y los átomos de diferentes elementos tienen diferentes números de protones. En otras palabras, el número de protones en un átomo define el elemento. Se conocen 118 elementos en este momento; el número de protones en los átomos varía de 1 para hidrógeno a 118 para Oganesson (Og).
El número de protones en un átomo se llama el número atómico.
El número atómico define el elemento. Un subíndice a la izquierda del símbolo de un elemento representa el número atómico. Por ejemplo,\(\ce{ _1H}\) muestra un protón en un átomo de hidrógeno, y\(\ce{_6C}\) muestra 6 protones en un átomo de carbono.
El número de protones más el número de neutrones en un átomo es el número de masa.
Un superíndice a la izquierda del símbolo de un elemento representa el número de masa. Por ejemplo,\(\ce{^1_1H}\) es un átomo de hidrógeno con número atómico 1, número de masa 1, y sin neutrones, mientras que\(\ce{^19_9F}\) es un átomo de flúor con 9 protones y 10 neutrones.
El número de electrones en un átomo es igual al número de protones menos la carga en el átomo.
El número de electrones es igual al número de protones en el caso de un átomo neutro, ya que no hay carga sobre un átomo neutro.
Un átomo neutro puede perder algunos electrones y convertirse en una partícula cargada positivamente, llamada catión.
La carga se representa como un superíndice en el lado derecho del símbolo del elemento, por ejemplo,\(\ce{^1_1H^+}\) es hidrógeno sin ningún electrón, es decir, 1 protón, 0 neutrones y 0 electrones. \(\ce{^20_40Ca^2+}\)es calcio con dos electrones menos que los protones, es decir, 20 protones, 20 neutrones y 18 electrones.
Un átomo puede ganar electrones y convertirse en una partícula cargada negativamente, llamada anión.
Por ejemplo,\(\ce{^16_8O^2-}\) es oxígeno con dos electrones más que protones sobre él, es decir, 8 protones, 8 neutrones y 10 electrones. A\(\ce{^19_9F^-}\) es flúor con un electrón más que protones sobre él, es decir, 9 protones, 10 neutrones y 10 electrones. La Fig. 2.3.1 ilustra la ganancia o pérdida de electrones de átomos neutros.
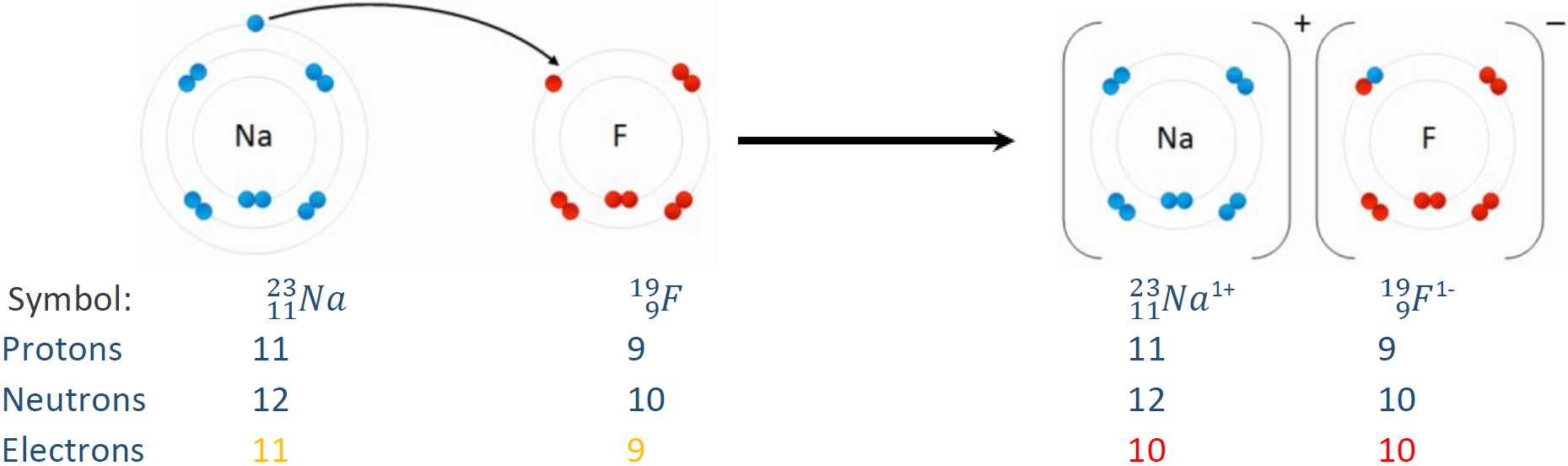
Cálculo del número de protones, neutrones y electrones
En general, un átomo de un elemento hipotético X se representa como\({ }_{Z}^{A} X^{I ~charge}\) donde Z es el número atómico, A es el número de masa, e I es un número entero igual al número de carga y carga el signo del número de carga: + o -.El número de protones, neutrones, y los electrones se calcula utilizando las siguientes fórmulas:
Número de protones = A,
Número de neutrones = A — Z, y
Número de electrones = Z — (carga I),
donde un cargo es un signo + o - del número de cargo.
Calcular el número de protones, neutrones y electrones en\(\ce{^16_8O}\),\(\ce{^16_8O^2-}\), y\(\ce{^16_8O^+}\)?
Solución
\(\ce{^16_8O}\): número de protones = Z = 8, número de neutrones = A — Z = 16-8 = 8,
y número de electrones = Z — (carga I) = 8 — 0 = 8.
\(\ce{^16_8O^2-}\): número de protones = Z = 8, número de neutrones = A — Z = 16-8 = 8,
y número de electrones = Z — (carga I) = 8 — (-2) = 8 + 2 = 10.
\(\ce{^16_8O^1+}\): número de protones = Z = 8, número de neutrones = A — Z = 16-8 = 8,
y número de electrones = Z — (carga I) = 8 — (+1) = 8 — 1 = 9.
Si el número de cargo I es de 1 en\({ }_{Z}^{A} X^{I ~charge}\), generalmente no se escribe, sino que se escribe un número más de uno. Por ejemplo,\(\ce{^16_8O^-}\) tiene cambio = -1,\(\ce{^16_8O^2-}\) tiene carga de carga -2, y\(\ce{^16_8O^+}\) tiene cargo = +1.
Isótopos
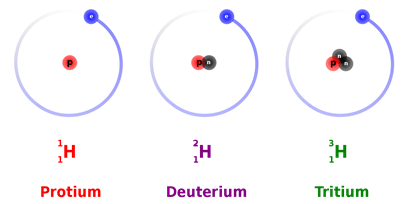
Todos los átomos del mismo elemento tienen el mismo número de protones pero pueden tener un número diferente de neutrones. Por ejemplo,\(\ce{^1_1H}\),\(\ce{^2_1H}\), y\(\ce{^3_1H}\) tienen neutrones iguales a 0, 1, y 2, respectivamente.
Los átomos del mismo elemento que tienen un número diferente de neutrones se denominan isótopos.
Por ejemplo,\(\ce{^1_1H}\),\(\ce{^2_1H}\), y\(\ce{^3_1H}\) son isótopos de hidrógeno ilustrados en la Fig. 2.3.2. Otro ejemplo es\(\ce{^6_3Li}\), y\(\ce{^7_3Li}\) son dos isótopos de litio. Las muestras naturales de elementos suelen tener relaciones casi constantes de isótopos. En el Cuadro 1 se enumeran algunos isótopos de elementos y su porcentaje de abundancia en muestras naturales típicas.
|
Element |
Isótopos |
Abundancia (%) |
|---|---|---|
|
Hidrógeno |
\(\ce{^1_1H}\) \(\ce{^2_1H}\) \(\ce{^3_1H}\) |
99.99 0.01 Despreciable |
|
Litio |
\(\ce{^6_3Li}\) \(\ce{^7_3Li}\) |
7.6 92.4 |
|
Carbono |
\(\ce{^12_6C}\) \(\ce{^13_6C}\) \(\ce{^14_6C}\) |
98.93 1.07 Despreciable |
|
Cloro |
\(\ce{^35_17Cl}\) \(\ce{^37_17Cl}\) |
75.78 24.22 |
|
Bromo |
\(\ce{^79_35Br}\) \(\ce{^81_35Br}\) |
50.69 49.31 |
|
Uranio |
\(\ce{^235_92U}\) \(\ce{^238_92U}\) |
0.72 99.28 |
Masa atómica
La masa atómica listada en la tabla periódica es el promedio ponderado de las masas de los isótopos presentes en una muestra natural del elemento.
La siguiente fórmula calcula la masa atómica:
\[\text { Atomic mass }=\sum[(\text { mass of isotope }) \times(\text { fractional abuncance of the isotope })\nonumber\]
, donde\(\sum\) significa la suma de todos los isótopos del elemento, la abundancia fraccional del isótopo es el% de abundancia dividido por 100. La Fig. 2.3.3. ilustra cómo se enumera la masa atómica en una tabla periódica.
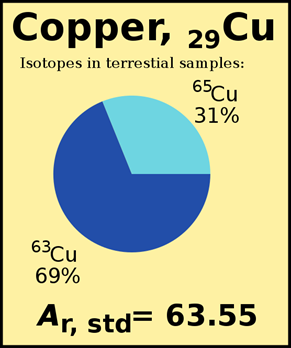
Calcular la masa atómica de cloro con dos isótopos en muestras naturales, es decir,\(\ce{^35_17Cl}\) de masa 34.969 amu y% de abundancia 75.78% y\(\ce{^37_17Cl}\) de masa 36.996 amu y% abundancia 24.22%.
Solución
Fórmula:\(\text { Atomic mass }=\sum[(\text { mass of isotope }) \times(\text { fractional abuncance of the isotope })\)
Conecte los valores dados en la fórmula y calcule:
\[\left(34.969 \mathrm{~amu} \times \frac{75.78}{100}\right)+\left(36.996 \mathrm{~amu} \times \frac{24.22}{100}\right)=35.45 \mathrm{~amu}\nonumber\]
- Las masas atómicas de isótopos son cercanas pero no iguales a sus números de masa. Por ejemplo,\(\ce{^35_17Cl}\) tiene número de masa masa = 35, pero la masa atómica de este isótopo es 34.969 amu como se muestra en el ejemplo anterior.
- La masa atómica promedio ponderada suele estar más cerca del número de masa del isótopo más abundante, por ejemplo, 35.45 amu en el ejemplo anterior está cerca del número de masa 35 del\(\ce{^35_17Cl}\) isótopo, que es el isótopo más abundante.
- La tabla periódica reporta la masa atómica calculada en el ejemplo anterior, es decir, el promedio ponderado de las masas de los isótopos presentes en la muestra natural del elemento.