Saltar al contenido principal
LibreTexts Español

5.2: Relaciones de volumen en ecuaciones químicas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    72413

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de aprendizaje
    • Identificar el volumen relativo de gas consumido o producido en base a una ecuación química equilibrada para una reacción.

    El comportamiento de los gases puede ser representado por leyes de gas como se discutirá con más detalle en el Capítulo 6. La ley de Avogadro establece que todos los gases (que muestran un comportamiento ideal) contienen el mismo número de moléculas en un mismo volumen (a la misma temperatura y presión). Así, las relaciones de volúmenes de gases involucrados en una reacción química vienen dadas por los coeficientes en la ecuación para la reacción, siempre que los volúmenes de gas se midan a la misma temperatura y presión.

    Podemos extender la ley de Avogadro (que el volumen de un gas es directamente proporcional al número de moles del gas) a reacciones químicas con gases: Los gases se combinan, o reaccionan, en proporciones definidas y simples por volumen, siempre que todos los volúmenes de gas se midan a la misma temperatura y presión. Por ejemplo, dado que los gases nitrógeno e hidrógeno reaccionan para producir gas amoníaco de acuerdo con la ecuación balanceada a continuación

    \[\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g) \nonumber \]

    un volumen dado de gas nitrógeno reacciona con tres veces ese volumen de gas hidrógeno para producir dos veces ese volumen de gas amoníaco, si la presión y la temperatura permanecen constantes.

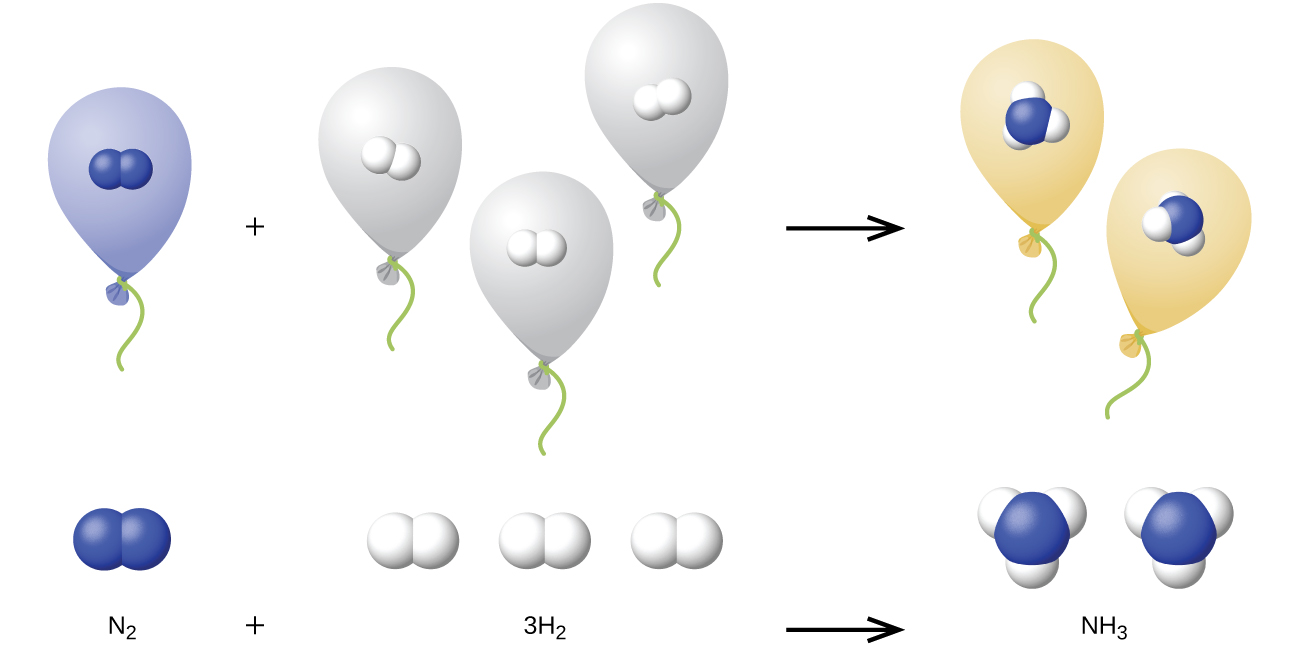
    La explicación de esto se ilustra en la Figura\(\PageIndex{1}\). Según la ley de Avogadro, volúmenes iguales de N 2, H 2 y NH 3 gaseosos, a la misma temperatura y presión, contienen el mismo número de moléculas. Debido a que una molécula de N 2 reacciona con tres moléculas de H 2 para producir dos moléculas de NH 3, el volumen de H 2 requerido es tres veces el volumen de N 2, y el volumen de NH 3 producido es dos veces el volumen de N 2.

    Figura\(\PageIndex{1}\): Un volumen de N 2 se combina con tres volúmenes de H 2 para formar dos volúmenes de NH 3.
    Este diagrama proporcionó modelos de la reacción química escrita con fórmulas en la parte inferior de la figura. La reacción está escrita; N subíndice 2 más 3 H subíndice 2 seguido de una flecha que apunta a la derecha al subíndice N H 3. Justo encima de las fórmulas, se proporcionan modelos de relleno de espacio. Por encima del subíndice N H 2, se enlazan dos esferas azules. Por encima de 3 H subíndice 2, se enlazan tres pares de dos esferas blancas ligeramente más pequeñas. Por encima del subíndice N H 3, se muestran dos moléculas compuestas cada una por una esfera azul central a la que se enlazan tres esferas blancas ligeramente más pequeñas. En la parte superior del diagrama, la reacción se ilustra con globos. A la izquierda hay un globo azul claro el cual está etiquetado como “N subíndice 2”. Este globo contiene un único modelo de relleno de espacio compuesto por dos esferas azules unidas. A este globo le sigue un signo más, luego tres globos grises cada uno de los cuales está etiquetado como “H subíndice 2”. Cada uno de estos globos contiene de manera similar un solo modelo de relleno de espacio compuesto por dos esferas blancas unidas. Estas esferas blancas son ligeramente más pequeñas que las esferas azules. Sigue una flecha que apunta a la derecha a dos globos de color verde claro, cada uno de los cuales está etiquetado como “N H subíndice 3”. Cada globo verde claro contiene un modelo de relleno de espacio compuesto por una única esfera azul central a la que están unidas tres esferas blancas ligeramente más pequeñas.
    Ejemplo\(\PageIndex{5}\): Reaction of Gases

    El propano, C 3 H 8 (g), se utiliza en parrillas de gas para proporcionar el calor para cocinar. ¿Qué volumen de O 2 (g) medido a 25 °C y 760 torr se requiere para reaccionar con 2.7 L de propano medido en las mismas condiciones de temperatura y presión? Supongamos que el propano se somete a combustión completa.

    Solución

    La relación de los volúmenes de C 3 H 8 y O 2 será igual a la relación de sus coeficientes en la ecuación equilibrada para la reacción:

    \ [\ begin {align}
    &\ ce {C3H8} (g) +\ ce {5O2} (g) ⟶ &&\ ce {3CO2} (g) +\ ce {4H2O} (l)\\
    \ ce {&1\: volumen + 5\: volúmenes &&3\: volúmenes + 4\: volúmenes}
    \ end {align}\ nonumber\]

    De la ecuación, vemos que un volumen de C 3 H 8 reaccionará con cinco volúmenes de O 2:

    \[\mathrm{2.7\cancel{L\:C_3H_8}×\dfrac{5\: L\:\ce{O2}}{1\cancel{L\:C_3H_8}}=13.5\: L\:\ce{O2}} \nonumber \]

    Se requerirá un volumen de 13.5 L de O 2 para reaccionar con 2.7 L de C 3 H 8.

    Ejercicio\(\PageIndex{5}\)

    Un tanque de acetileno para un soplete de oxiacetileno proporciona 9340 L de gas acetileno, C 2 H 2, a 0 °C y 1 atm. ¿Cuántos tanques de oxígeno, cada uno proporcionando 7.00 × 10 3 L de O 2 a 0 °C y 1 atm, se requerirán para quemar el acetileno?

    \[\ce{2C2H2 + 5O2⟶4CO2 + 2H2O} \nonumber \]

    Contestar

    Tanques 3.34 (2.34 × 10 4 L)

    Ejemplo\(\PageIndex{6}\): Volumes of Reacting Gases

    El amoníaco es un importante fertilizante y químico industrial. Supongamos que se fabricó un volumen de 683 mil millones de pies cúbicos de amoníaco gaseoso, medido a 25 °C y 1 atm. ¿Qué volumen de H 2 (g), medido en las mismas condiciones, se requirió para preparar esta cantidad de amoníaco por reacción con N 2?

    \[\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g) \nonumber \]
    Solución

    Debido a que volúmenes iguales de H 2 y NH 3 contienen igual número de moléculas y cada tres moléculas de H 2 que reaccionan producen dos moléculas de NH 3, la relación de los volúmenes de H 2 y NH 3 será igual a 3:2. Dos volúmenes de NH 3, en este caso en unidades de mil millones de pies 3, se formarán a partir de tres volúmenes de H 2:

    \[\mathrm{683\cancel{billion\:ft^3\:NH_3}×\dfrac{3\: billion\:ft^3\:H_2}{2\cancel{billion\:ft^3\:NH_3}}=1.02×10^3\:billion\:ft^3\:H_2} \nonumber \]

    La fabricación de 683 mil millones de pies 3 de NH 3 requirió 1020 mil millones de pies 3 de H 2. (A 25 °C y 1 atm, este es el volumen de un cubo con una longitud de borde de aproximadamente 1.9 millas).

    Ejercicio\(\PageIndex{6}\)

    ¿Qué volumen de O 2 (g) medido a 25 °C y 760 torr se requiere para reaccionar con 17.0 L de etileno, C 2 H 4 (g), medido en las mismas condiciones de temperatura y presión? Los productos son CO 2 y vapor de agua.

    Contestar

    51.0 L

    Resumen

    La ley de Avogadro puede ser utilizada para determinar el volumen de reactivo (s) gaseoso (s) o producto (s) basado en una ecuación química equilibrada.

    Colaboradores y Atribuciones

    5.2: Relaciones de volumen en ecuaciones químicas is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.