5.4: Conversiones Masa Molar-a-Masa y Masa a Mola
- Page ID
- 72427
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Realizar conversiones entre masa y moles de una sustancia.
- Convertir de masa o moles de una sustancia a masa o moles de otra sustancia en una reacción química.
- Utilizar una ecuación química equilibrada para determinar las relaciones molares entre sustancias.
Masa molar
La masa molar de cualquier sustancia es la masa en gramos de un mol de partículas representativas de esa sustancia. Las partículas representativas pueden ser átomos, moléculas o unidades de fórmula de compuestos iónicos. Esta relación se utiliza frecuentemente en el laboratorio. El tipo más simple de manipulación que utiliza la masa molar como factor de conversión es una conversión mola-masa (o su inversa, una conversión masa-mol). En tal conversión, utilizamos la masa molar de una sustancia como factor de conversión para convertir unidades molares en unidades de masa (o, a la inversa, unidades de masa en unidades molares).
También se estableció que 1 mol de Al tiene una masa de 26.98 g (Ejemplo). Declarado matemáticamente,
1 mol Al = 26.98 g Al
Podemos dividir ambos lados de esta expresión por cada lado para obtener uno de los dos posibles factores de conversión:
\[\mathrm{\dfrac{1\: mol\: Al}{26.98\: g\: Al}\, and\, \dfrac{26.98\: g\: Al}{1\: mol\: Al}} \label{Eq1} \]
El primer factor de conversión se puede utilizar para convertir de masa a moles, y el segundo convierte de moles a masa. Ambos pueden ser utilizados para resolver problemas que serían difíciles de hacer “a simple vista”.
¿Cuál es la masa de 3.987 mol de Al?
Solución
| Pasos para la resolución de problemas | Ejemplo |
|---|---|
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. | Dado: 3.987 mol de Al Encuentra: g Al |
| Enumerar otras cantidades conocidas | 1 mol Al = 26.98 g Al |
| Preparar un mapa conceptual y utilizar el factor de conversión adecuado. |  |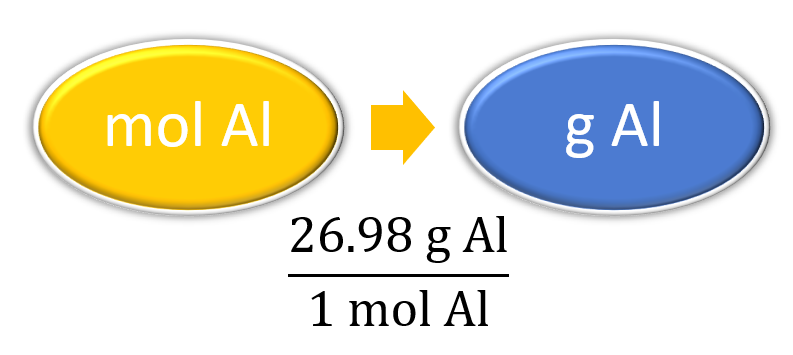
| Cancelar unidades y calcular. | \(3.987 \: \cancel{\text{mol} \: \ce{Al}} \times \dfrac{26.98 \: \text{g} \: \ce{Al}}{1 \: \cancel{\text{mol} \: \ce{Al}}} = 107.6 \: \text{g} \: \ce{Al}\) |
| Piensa en tu resultado. | El valor calculado tiene sentido porque es casi cuatro veces la masa para 1 mol de aluminio. Nuestra respuesta final se expresa a cuatro cifras significativas. |
¿Cuántos moles están presentes en 100. g de Al? (Pista: tendrás que usar el otro factor de conversión que obtuvimos para el aluminio.)
Responder
3.71 g Al
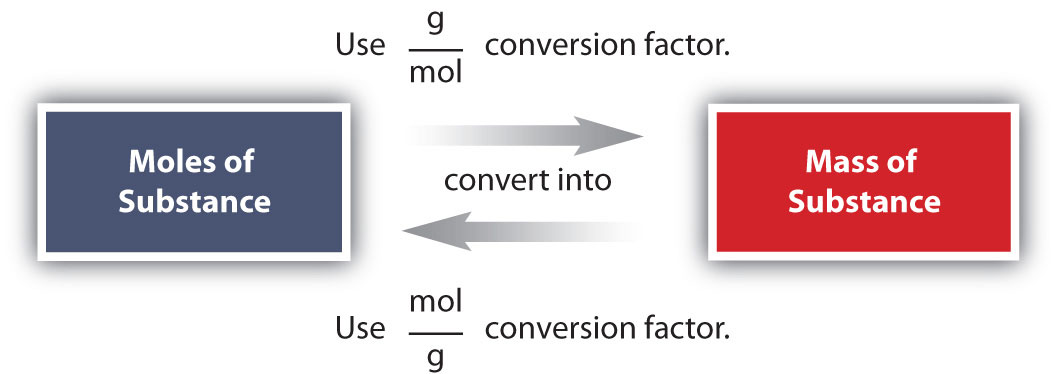
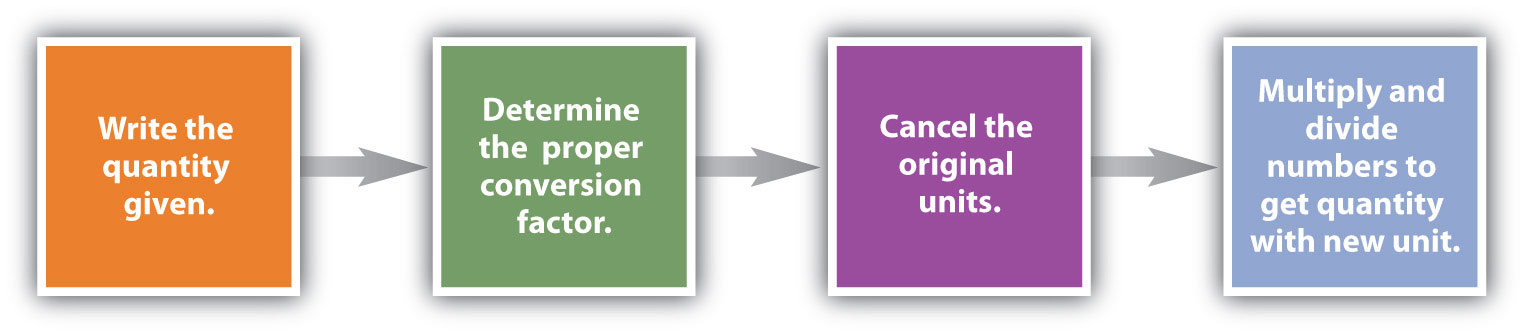
Conversiones como esta son posibles para cualquier sustancia, siempre y cuando se conozca (o pueda determinarse) la masa atómica adecuada, la masa de fórmula o la masa molar y se exprese en gramos por mol. La figura\(\PageIndex{1}\) es una gráfica para determinar qué factor de conversión se necesita, y la figura\(\PageIndex{2}\) es un diagrama de flujo para los pasos necesarios para realizar una conversión.
Supongamos que para cierto experimento se necesitan 3.00 moles de cloruro de calcio\(\left( \ce{CaCl_2} \right)\). Dado que el cloruro de calcio es un sólido, sería conveniente utilizar una balanza para medir la masa que se necesita. El análisis dimensional te permitirá calcular la masa de la\(\ce{CaCl_2}\) que debes medir como se muestra en Ejemplo\(\PageIndex{3}\).
Calcular la masa de 3.00 moles de cloruro de calcio (CaCl 2).
Solución
| Pasos para la resolución de problemas | Ejemplo |
|---|---|
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. | Dado: 3.00 moles de CaCl 2 Encuentra: g CaCl 2 |
| Enumerar otras cantidades conocidas | 1 ml CaCl 2 = 110.98 g CaCl 2 |
| Preparar un mapa conceptual y utilizar el factor de conversión adecuado. |  |
| Cancelar unidades y calcular. | \(3.00 \: \cancel{\text{mol} \: \ce{CaCl_2}} \times \dfrac{110.98 \: \text{g} \: \ce{CaCl_2}}{1 \: \cancel{\text{mol} \: \ce{CaCl_2}}} = 333 \: \text{g} \: \ce{CaCl_2}\) |
| Piensa en tu resultado. |
¿Cuál es la masa\(7.50 \: \text{mol}\) de (óxido de calcio)\(\ce{CaO}\)?
- Respuesta:
- 420.60 g
¿Cuántos moles están presentes en 108 gramos de agua?
Solución
| Pasos para la resolución de problemas | Ejemplo |
|---|---|
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. | Dado: 108 g H 2 O Encuentra: mol H 2 O |
| Enumerar otras cantidades conocidas | \(1 \: \text{mol} \: \ce{H_2O} = 18.02 \: \text{g}\)H 2 O |
| Preparar un mapa conceptual y utilizar el factor de conversión adecuado. |  |
| Cancelar unidades y calcular. | \(108 \: \cancel{\text{g} \: \ce{H_2O}} \times \dfrac{1 \: \text{mol} \: \ce{H_2O}}{18.02 \: \cancel{\text{g} \: \ce{H_2O}}} = 5.99 \: \text{mol} \: \ce{H_2O}\) |
| Piensa en tu resultado. |
¿Cuál es la masa\(7.50 \: \text{mol}\) de gas Nitrógeno\(\ce{N2}\)?
- Respuesta:
- 210 g
Relaciones Topo y Masa en Ecuaciones Químicas
Hemos establecido que una ecuación química equilibrada se equilibra tanto en términos de moles como de átomos o moléculas. Hemos utilizado ecuaciones equilibradas para establecer relaciones, ahora en términos de moles de materiales, que podemos usar como factores de conversión para responder preguntas estequiométricas, como cuántos moles de sustancia A reaccionan con tantos moles de reactivo B. Podemos extender aún más esta técnica. Recordemos que podemos relacionar una cantidad molar con una cantidad de masa usando masa molar. Podemos usar esa capacidad para responder preguntas estequiométricas en términos de las masas de una sustancia en particular, además de los moles. Hacemos esto usando la siguiente secuencia:
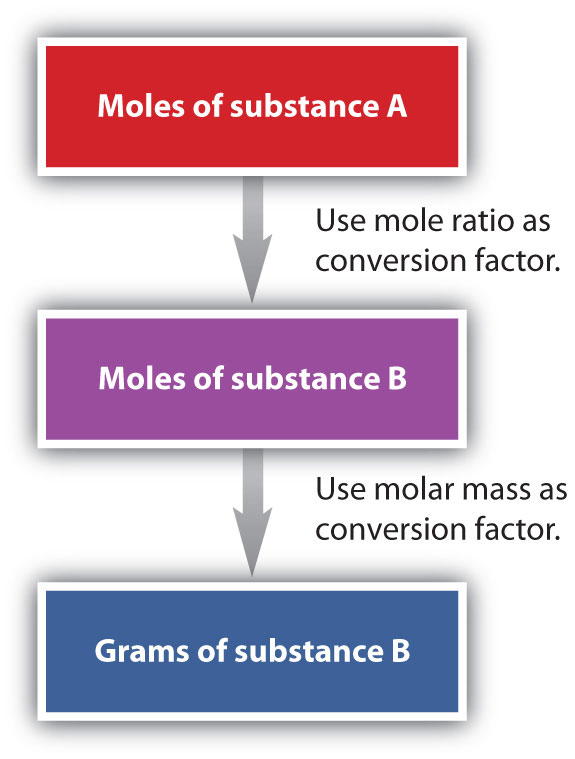
Colectivamente, estas conversiones se denominan cálculos de masa molar.
Como ejemplo, considere la ecuación química balanceada
\[Fe_2O_3 + 3SO_3 \rightarrow Fe_2(SO_4)_3 \nonumber \]
Si tenemos 3.59 mol de Fe 2 O 3, ¿cuántos gramos de SO 3 pueden reaccionar con él? Usando la secuencia de cálculo de masa molar, podemos determinar la masa requerida de SO 3 en dos pasos. Primero, construimos la relación molar apropiada, determinada a partir de la ecuación química equilibrada, para calcular el número de moles de SO 3 necesarios. Luego usando la masa molar de SO 3 como factor de conversión, determinamos la masa que tiene este número de moles de SO 3.
Como de costumbre, comenzamos con la cantidad que nos dieron:
\[\mathrm{3.59\: \cancel{ mol\: Fe_2O_3 } \times \left( \dfrac{3\: mol\: SO_3}{1\: \cancel{ mol\: Fe_2O_3}} \right) =10.77\: mol\: SO_3} \label{Eq2} \]
El mol Fe 2 O 3 unidades cancelan, dejando mol SO 3 unidad. Ahora, tomamos esta respuesta y la convertimos a gramos de SO 3, usando la masa molar de SO 3 como factor de conversión:
\[\mathrm{10.77\: \bcancel{mol\: SO_3} \times \left( \dfrac{80.06\: g\: SO_3}{1\: \bcancel{ mol\: SO_3}} \right) =862\: g\: SO_3} \label{Eq3} \]
Nuestra respuesta final se expresa a tres cifras significativas. Así, en un proceso de dos etapas, encontramos que 862 g de SO 3 reaccionarán con 3.59 mol de Fe 2 O 3. Muchos problemas de este tipo pueden ser respondidos de esta manera.
El mismo problema de dos pasos también se puede resolver en una sola línea, en lugar de como dos pasos separados, de la siguiente manera:
\[ 3.59 \cancel{\, mol \, Fe_2O_3} \times \underbrace{\left( \dfrac{ 3 \bcancel{ \, mol\, SO_3}}{ 1 \cancel{\, mol\, Fe_2O_3}} \right)}_{\text{converts to moles of SO}_3} \times \underbrace{ \left( \dfrac{ 80.06 {\, g \, SO_3}}{ 1 \, \bcancel{ mol\, SO_3}} \right)}_{\text{converts to grams of SO}_3} = 862\, g\, SO_3 \nonumber \]
Obtenemos exactamente la misma respuesta al combinar todos los pasos matemáticos juntos como lo hacemos cuando calculamos un paso a la vez.
¿Cuántos moles de HCl se producirán cuando se hagan reaccionar 249 g de AlCl 3 de acuerdo con esta ecuación química?
\[2AlCl_3 + 3H_2O(ℓ) → Al_2O_3 + 6HCl(g) \nonumber \]
Solución
| Pasos para la resolución de problemas | Ejemplo |
|---|---|
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. | Dado: 249 g AlCl 3 Encuentra: moles HCl |
| Enumerar otras cantidades conocidas | 1 mol de AlCl 3 = 133.33 g/mol 6 mol de HCl a 2 mol de AlCl 3 |
| Preparar un mapa conceptual y utilizar el factor de conversión adecuado. |  |
| Cancelar unidades y calcular. | \(249\, \cancel{g\, AlCl_{3}}\times \dfrac{1\, \cancel{mol\, AlCl_{3}}}{133.33\, \cancel{g\, AlCl_{3}}}\times \dfrac{6\, mol\, HCl}{2\, \cancel{mol\, AlCl_{3}}}=5.60\, mol\, HCl\) |
| Piensa en tu resultado. | Dado que 249 g de AlCl 3 es menor a 266.66 g, la masa para 2 moles de AlCl 3 y la relación es de 6 mol de HCl a 2 mol de AlCl 3, la respuesta debe ser menor a 6 moles de HCl. |
¿Cuántos moles de Al 2 O 3 se producirán cuando 23.9 g de H 2 O reaccionen de acuerdo con esta ecuación química?
\[2AlCl_3 + 3H_2O(ℓ) → Al_2O_3 + 6HCl(g) \nonumber \]
- Contestar
- 0.442 mol Al 2 O 3
Relaciones Molares en Ecuaciones Químicas
Anteriormente, aprendiste a equilibrar las ecuaciones químicas comparando los números de cada tipo de átomo en los reactivos y productos. Los coeficientes frente a las fórmulas químicas representan el número de moléculas o unidades de fórmula (dependiendo del tipo de sustancia). Aquí, extenderemos el significado de los coeficientes en una ecuación química.
Considera la ecuación química simple
\[2H_2 + O_2 → 2H_2O \nonumber \]
La convención para escribir ecuaciones químicas balanceadas es usar la relación de número entero más baja para los coeficientes. Sin embargo, la ecuación se equilibra siempre y cuando los coeficientes estén en una relación 2:1:2. Por ejemplo, esta ecuación también se equilibra si la escribimos como
\[4H_2 + 2O_2 → 4H_2O \nonumber \]
La relación de los coeficientes es 4:2:4, que se reduce a 2:1:2. La ecuación también se equilibra si la escribiéramos como
\[22H_2 + 11O_2 → 22H_2O \nonumber \]
porque 22:11:22 también reduce a 2:1:2.
Supongamos que queremos usar números más grandes. Considere los siguientes coeficientes:
\[12.044 \times 10^{23}\; H_2 + 6.022 \times 10^{23}\; O_2 → 12.044 \times 10^{23}\; H_2O \nonumber \]
Estos coeficientes también tienen la relación 2:1:2 (verifíquelo y vea), por lo que esta ecuación se equilibra. Pero 6.022 × 10 23 es 1 mol, mientras que 12.044 × 10 23 es 2 mol (y el número se escribe de esa manera para que esto sea más obvio), así podemos simplificar esta versión de la ecuación escribiéndola como
\[2 \;mol\; H_2 + 1\; mol\; O_2 → 2 \;mol\; H_2O \nonumber \]
Podemos dejar de lado la palabra mol y no escribir el coeficiente 1 (como es nuestro hábito), por lo que la forma final de la ecuación, aún equilibrada, es
\[2H_2 + O_2 → 2H_2O \nonumber \]
Ahora interpretamos los coeficientes como referentes a cantidades molares, no a moléculas individuales. ¿La lección? Las ecuaciones químicas balanceadas se equilibran no solo a nivel molecular sino también en términos de cantidades molares de reactivos y productos. Así, podemos leer esta reacción como “dos moles de hidrógeno reaccionan con un mol de oxígeno para producir dos moles de agua”.
De la misma manera, las proporciones que construimos para describir la reacción de las moléculas también se pueden construir en términos de moles en lugar de moléculas. Para la reacción en la que se combinan hidrógeno y oxígeno para hacer agua, por ejemplo, podemos construir las siguientes proporciones:
\[\mathrm{\dfrac{2\: mol\: H_2}{1\: mol\: O_2}\: or\: \dfrac{1\: mol\: O_2}{2\: mol\: H_2}} \nonumber \]
\[\mathrm{\dfrac{2\: mol\: H_2O}{1\: mol\: O_2}\: or\: \dfrac{1\: mol\: O_2}{2\: mol\: H_2O}} \nonumber \]
\[\mathrm{\dfrac{2\: mol\: H_2}{2\: mol\: H_2O}\: or\: \dfrac{2\: mol\: H_2O}{2\: mol\: H_2}} \nonumber \]
Podemos usar estas proporciones para determinar qué cantidad de una sustancia, en moles, reaccionará con o producirá un número dado de moles de una sustancia diferente. El estudio de las relaciones numéricas entre los reactivos y los productos en reacciones químicas equilibradas se denomina estequiometría.
¿Cuántos moles de oxígeno reaccionan con hidrógeno para producir 27.6 mol de H 2 O?
Solución
| Pasos para la resolución de problemas | Ejemplo |
|---|---|
| Encuentre una ecuación equilibrada que describa la reacción |
Desbalanceado: H 2 + O 2 → H 2 O Equilibrado: 2 H 2 + O 2 → 2 H 2 O |
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. | Dado: moles H 2 O Encuentra: moles oxígeno |
| Enumerar otras cantidades conocidas | 1 mol O 2 = 2 mol H 2 O |
| Preparar un mapa conceptual y utilizar el factor de conversión adecuado. |  |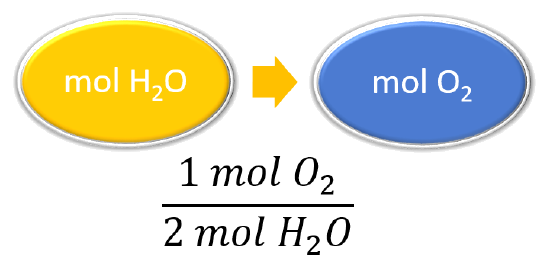
| Cancelar unidades y calcular. |
\(\mathrm{\cancel{27.6\: mol\: H_2O}\times\dfrac{1\: mol\: O_2}{\cancel{2\: mol\: H_2O}}=13.8\: mol\: O_2}\) Para producir 27.6 mol de H 2 O, 13.8 mol de O 2 reaccionan. |
| Piensa en tu resultado. | Dado que cada mol de oxígeno produce el doble de moles de agua, tiene sentido que la cantidad producida sea mayor que la cantidad de reactivo |
¿Cuántos moles de amoníaco se producen si se hacen reaccionar 4.20 moles de hidrógeno con un exceso de nitrógeno?
Solución
| Pasos para la resolución de problemas | Ejemplo |
|---|---|
| Encuentre una ecuación equilibrada que describa la reacción |
Desbalanceado: N 2 + H 2 → NH 3 Equilibrado: N 2 + 3 H 2 → 2 NH 3 |
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. |
Dado:\(\ce{H_2} = 4.20 \: \text{mol}\) Encuentra:\(\text{mol}\) de\(\ce{NH_3}\) |
| Enumerar otras cantidades conocidas | 3 mol H 2 = 2 mol NH 3 |
| Preparar un mapa conceptual y utilizar el factor de conversión adecuado. |  |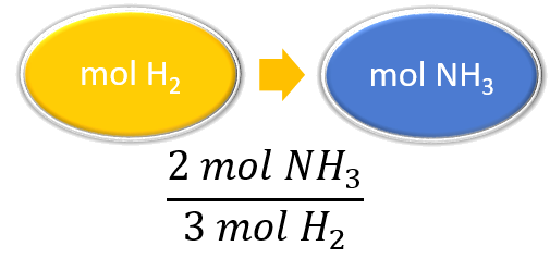
| Cancelar unidades y calcular. |
\(\cancel{4.20 \: \text{mol} \: H_2} \times \dfrac{2 \: \text{mol} \: NH_3}{\cancel{3 \: \text{mol} \: H_2}} = 2.80 \: \text{mol} \: NH_3\) La reacción\(4.20 \: \text{mol}\) de hidrógeno con exceso de nitrógeno produce\(2.80 \: \text{mol}\) de amoníaco |
| Piensa en tu resultado. | El resultado corresponde a la relación 3:2 de hidrógeno a amoníaco de la ecuación equilibrada. |
- Dada la siguiente ecuación química equilibrada,\[\ce{C5H12 + 8O2 → 5CO2 + 6H2O} \nonumber \] ¿cuántos moles de H 2 O se pueden formar si reaccionaran 0.0652 mol de C 5 H 12?
- Equilibrar la siguiente ecuación desequilibrada y determinar cuántos moles de H 2 O se producen cuando reaccionan 1.65 mol de NH 3. \[\ce{NH3 + O2 → N2 + H2O} \nonumber \]
- Respuesta a:
- 3.14 mol H 2 O
- Respuesta b:
- 4NH 3 + 3O 2 → 2N 2 + 6H 2 O; 2.48 mol H 2 O
Relaciones de Masa en Ecuaciones Químicas
Es un pequeño paso desde los cálculos de masa molar hasta los cálculos de masa y masa. Si comenzamos con una masa conocida de una sustancia en una reacción química (en lugar de un número conocido de moles), podemos calcular las masas correspondientes de otras sustancias en la reacción. El primer paso en este caso es convertir la masa conocida en moles, utilizando la masa molar de la sustancia como factor de conversión. Entonces, y solo entonces, usamos la ecuación química balanceada para construir un factor de conversión para convertir esa cantidad en moles de otra sustancia, que a su vez se puede convertir en una masa correspondiente. Secuencialmente, el proceso es el siguiente:
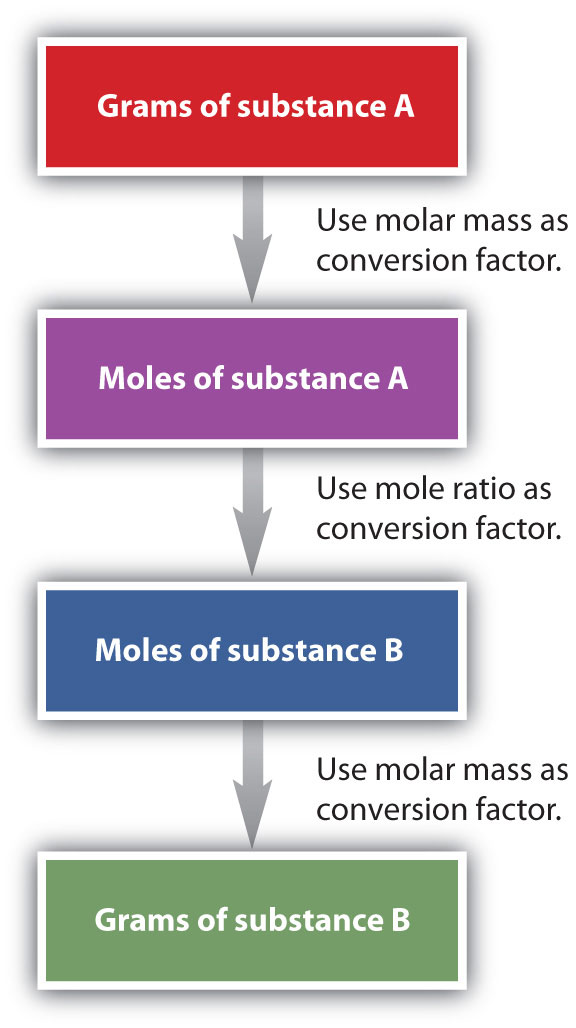
Este proceso de tres partes se puede llevar a cabo en tres etapas discretas o combinarse en un solo cálculo que contiene tres factores de conversión. El siguiente ejemplo ilustra ambas técnicas.
El nitrato amónico se descompone en monóxido de dinitrógeno y agua de acuerdo con la siguiente ecuación.
\[\ce{NH_4NO_3} \left( s \right) \rightarrow \ce{N_2O} \left( g \right) + 2 \ce{H_2O} \left( l \right) \nonumber \]
En cierto experimento,\(45.7 \: \text{g}\) de nitrato de amonio se descompone. Encuentra la masa de cada uno de los productos formados.
| Pasos para la resolución de problemas | Ejemplo\(\PageIndex{2}\) |
|---|---|
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. | \ (\ PageIndex {2}\) ">
Dado:\(45.7 \: \text{g} \: \ce{NH_4NO_3}\) Masa\(\ce{N_2O} = ? \: \text{g}\) Masa\(\ce{H_2O} = ? \: \text{g}\) |
| Enumerar otras cantidades conocidas | \ (\ PageIndex {2}\) ">
1 mol\(\ce{NH_4NO_3} = 80.06 \: \text{g/mol}\) 1 mol\(\ce{N_2O} = 44.02 \: \text{g/mol}\) 1 mol\(\ce{H_2O} = 18.02 \: \text{g/mol}\) 1 mol NH 4 NO 3 a 1 mol N 2 O a 2 mol H 2 O |
| Prepare dos mapas conceptuales y utilice el factor de conversión adecuado. | \ (\ PageIndex {2}\) ">
|
| Cancelar unidades y calcular. | \ (\ PageIndex {2}\) ">
\(45.7 \: \text{g} \: \ce{NH_4NO_3} \times \dfrac{1 \: \text{mol} \: \ce{NH_4NO_3}}{80.06 \: \text{g} \: \ce{NH_4NO_3}} \times \dfrac{1 \: \text{mol} \: \ce{N_2O}}{1 \: \text{mol} \: \ce{NH_4NO_3}} \times \dfrac{44.02 \: \text{g} \: \ce{N_2O}}{1 \: \text{mol} \: \ce{N_2O}} = 25.1 \: \text{g} \: \ce{N_2O}\) \(45.7 \: \text{g} \: \ce{NH_4NO_3} \times \dfrac{1 \: \text{mol} \: \ce{NH_4NO_3}}{80.06 \: \text{g} \: \ce{NH_4NO_3}} \times \dfrac{2 \: \ce{H_2O}}{1 \: \text{mol} \: \ce{NH_4NO_3}} \times \dfrac{18.02 \: \text{g} \: \ce{H_2O}}{1 \: \text{mol} \: \ce{H_2O}} = 20.6 \: \text{g} \: \ce{H_2O}\) |
| Piensa en tu resultado. | \ (\ PageIndex {2}\) ">La masa total de los dos productos es igual a la masa de nitrato amónico que se descompuso, demostrando la ley de conservación de la masa. Cada respuesta tiene tres cifras significativas. |
El metano puede reaccionar con el cloro elemental para producir tetracloruro de carbono (\(\ce{CCl_4}\)). La ecuación química equilibrada es la siguiente.
\[\ce{CH4 (g) + 4 Cl2 (g) → CCl2 (l) + 4 HCl (l) } \nonumber \]
¿Cuántos gramos de HCl se producen por la reacción de 100.0g de\(\ce{CH4}\)?
- Contestar
- 908.7g HCl
Resumen
- Se describen los cálculos que implican conversiones entre moles de una sustancia y la masa de esa sustancia.
- La reacción química equilibrada se puede utilizar para determinar las relaciones molares y de masa entre las sustancias.
Colaboradores y Atribuciones
- TextMap: The Basics of GOB Chemistry (Ball et al.)
Henry Agnew (UC Davis)