5.5: Soluciones
- Page ID
- 72414
- Aprende algo de terminología que involucra soluciones.
- Exprese la cantidad de soluto en una solución en diversas unidades de concentración.
Cuando una sustancia se disuelve en otra, se forma una solución. Una solución es una mezcla homogénea que consiste en un soluto disuelto en un disolvente. El soluto es la sustancia que se está disolviendo, mientras que el disolvente es el medio de disolución. Las soluciones se pueden formar con muchos tipos y formas diferentes de solutos y solventes. En este capítulo, nos centraremos en la solución donde el solvente es el agua. Una solución acuosa es agua que contiene una o más sustancias disueltas. Las sustancias disueltas en una solución acuosa pueden ser sólidos, gases u otros líquidos.
Para ser una verdadera solución, una mezcla debe ser estable. Cuando el azúcar se disuelve completamente en agua, puede permanecer durante un tiempo indefinido, y el azúcar no se sedimentará de la solución. Además, si la solución de azúcar-agua se pasa a través de un filtro, permanecerá con el agua. Esto se debe a que las partículas disueltas en una solución son muy pequeñas, generalmente menores que\(1 \: \text{nm}\) en diámetro. Las partículas de soluto pueden ser átomos, iones o moléculas, dependiendo del tipo de sustancia que se haya disuelto. El agua generalmente disuelve la mayoría de los compuestos iónicos y moléculas polares. Las moléculas no polares, como las que se encuentran en la grasa o el aceite, no se disuelven en agua.
Concentraciones de solución
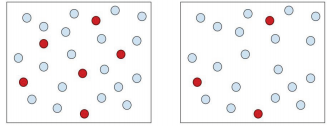
hasta el más concentrado (a la derecha).
Una solución concentrada es aquella en la que hay una gran cantidad de soluto en una cantidad dada de disolvente. Una solución diluida es aquella en la que hay una pequeña cantidad de soluto en una cantidad dada de disolvente. Una solución diluida es una solución concentrada que ha sido, en esencia, diluida. Piense en los envases de jugo congelado que compra en la tienda de abarrotes. Lo que tienes que hacer es tomar el jugo congelado del interior de estos recipientes y generalmente vaciarlo en 3 o 4 veces el tamaño del recipiente lleno de agua para mezclarlo con el concentrado de jugo y hacer tu recipiente de jugo. Por lo tanto, estás diluyendo el jugo concentrado. Cuando hablamos de soluto y solvente, la solución concentrada
tiene mucho soluto versus la solución diluida que tendría una cantidad menor de soluto.
Los términos “concentrado” y “diluido” proporcionan métodos cualitativos para describir la concentración. Si bien las observaciones cualitativas son necesarias y tienen su lugar en cada parte de la ciencia, incluida la química, hemos visto a lo largo de nuestro estudio de la ciencia que existe una necesidad definitiva de mediciones cuantitativas en la ciencia. Esto es particularmente cierto en la química de soluciones. En esta sección, exploraremos algunos métodos cuantitativos para expresar la concentración de la solución.
Para definir una solución con precisión, necesitamos exponer su concentración: cuánto soluto se disuelve en una cierta cantidad de disolvente. Palabras como diluida o concentrada se utilizan para describir soluciones que tienen poco o mucho soluto disuelto, respectivamente, pero estos son términos relativos cuyos significados dependen de diversos factores. Cuando decimos que el vinagre es ácido\(5\%\) acético en el agua, estamos dando la concentración. Si dijéramos que la mezcla era ácido\(10\%\) acético, esto estaría más concentrado que la solución de vinagre y sabemos exactamente por cuánto.
Molaridad
Una forma de expresar la concentración es dar el número de moles de soluto por unidad de volumen de solución. De todas las medidas cuantitativas de concentración, la molaridad es la utilizada con mayor frecuencia por los químicos. La molaridad se define como el número de moles de soluto por litro de solución.
\[\mathrm{molarity=\dfrac{number\: of\: moles\: of\: solute}{number\: of\: liters\: of\: solution}} \label{defMolarity} \]
El símbolo de molaridad es\(\text{M}\) o moles/litro. Los químicos también usan corchetes para indicar una referencia a la molaridad de una sustancia. Por ejemplo, la expresión\(\left[ \ce{Ag^+} \right]\) se refiere a la molaridad del ion plata en solución. Las concentraciones de solución expresadas en molaridad son las más fáciles de calcular pero las más difíciles de hacer en el laboratorio. Dichas unidades de concentración son útiles para discutir reacciones químicas en las que un soluto es un producto o un reactivo. La masa molar se puede usar entonces como factor de conversión para convertir cantidades en moles a cantidades en gramos.
Es importante recordar que “mol” en esta expresión se refiere a moles de soluto y que “L” se refiere a litros de solución. Por ejemplo, si tienes 1.5 mol de NaCl disueltos en 0.500 L de solución, su molaridad es por lo tanto
\[\mathrm{\dfrac{1.5\: mol\: NaCl}{0.500\: L\: solution}=3.0\: M\: NaCl} \nonumber \]
A veces se agrega (ac) cuando el solvente es agua, como en “NaCl 3.0 M (ac)”. Se leería como “una solución de cloruro de sodio 3.00 molar”, lo que significa que hay 3.00 moles de NaOH disueltos por litro de solución.
Asegúrese de señalar que la molaridad se calcula como el volumen total de toda la solución, ¡no solo el volumen de disolvente! El soluto contribuye al volumen total.
Si la cantidad del soluto se da en unidades de masa, debe convertir unidades de masa en unidades molares antes de usar la definición de molaridad para calcular la concentración. Por ejemplo, ¿cuál es la concentración molar de una solución de 22.4 g de HCl disueltos en 1.56 L?
Primero, convertir la masa de soluto en moles usando la masa molar de HCl (36.5 g/mol):
\[22.4\cancel{gHCl}\times \dfrac{1\: mol\: HCl}{36.5\cancel{gHCl}}=0.614\, mol\; HCl \nonumber \]
Ahora podemos usar la definición de molaridad para determinar una concentración:
\[M \: =\: \dfrac{0.614\: mol\: HCl}{1.56L\: solution}=0.394\, M HCl \nonumber \]
Antes de que se pueda calcular una concentración de molaridad, la cantidad del soluto debe expresarse en moles, y el volumen de la solución debe expresarse en litros, como se demuestra en el siguiente ejemplo.
Una solución se prepara disolviendo\(42.23 \: \text{g}\)\(\ce{NH_4Cl}\) en agua suficiente para hacer\(500.0 \: \text{mL}\) de solución. Calcular su molaridad.
Solución
Pasos para la resolución de problemas |
Ejemplo |
|---|---|
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. |
Dado: Masa\(= 42.23 \: \text{g} \: \ce{NH_4Cl}\) Solución de volumen\(= 500.0 \: \text{mL} = 0.5000 \: \text{L}\) Encuentra: Molaridad =? M |
| Enumere otras cantidades conocidas. | Masa molar\(\ce{NH_4Cl} = 53.50 \: \text{g/mol}\) |
| Planear el problema. |
1. La masa del cloruro amónico se convierte primero en moles.
2. Entonces se calcula la molaridad dividiendo por litros. Tenga en cuenta que el volumen dado se ha convertido a litros. \(\mathrm{M=\frac{mol\: NH_4Cl}{L\: solution}} \) |
| Cancelar unidades y calcular. |
Ahora sustituya las cantidades conocidas en la ecuación y resuelva. \(\begin{align} 42.23 \ \cancel{\text{g} \: \ce{NH_4Cl}} \times \dfrac{1 \: \text{mol} \: \cancel{\ce{NH_4Cl}}}{53.50 \: \text{g} \: \ce{NH_4Cl}} &= 0.7893 \: \text{mol} \: \ce{NH_4Cl} \\ \dfrac{0.7893 \: \text{mol} \: \ce{NH_4Cl}}{0.5000 \: \text{L solution}} &= 1.579 \: \text{M} \end{align}\) |
| Piensa en tu resultado. | La molaridad es\(1.579 \: \text{M}\), es decir, que un litro de la solución contendría\(1.579 \: \text{mol} \: \ce{NH_4Cl}\). Cuatro cifras significativas son apropiadas. |
¿Cuál es la molaridad de una solución hecha cuando se disuelven 66.2 g de C 6 H 12 O 6 para hacer 235 mL de solución?
- Contestar
-
1.57 M C 6 H 12 O 6
¿Cuál es la concentración, en\(\text{mol/L}\), dónde\(137 \: \text{g}\) de se\(\ce{NaCl}\) ha disuelto en suficiente agua para hacer\(500 \: \text{mL}\) de solución?
- Contestar
-
4.69 M NaCl
La Figura\(\PageIndex{1}\) ilustra cómo se prepara una solución con la cantidad medida de un soluto sólido y el volumen final deseado de la solución.
Concentraciones porcentuales
Existen varias formas de expresar la concentración de una solución mediante el uso de un porcentaje. El porcentaje se puede determinar adicionalmente de una de dos maneras: (1) la relación de la masa del soluto dividida por la masa de la solución o (2) la relación del volumen del soluto dividida por el volumen de la solución.
Porcentaje por Volumen
El porcentaje de soluto en una solución se puede determinar más fácilmente por volumen cuando el soluto y el disolvente son ambos líquidos. El volumen del soluto dividido por el volumen de la solución expresado como porcentaje produce el porcentaje por volumen\(\left( \frac{\text{volume}}{\text{volume}} \right)\) de la solución. Si se hace una solución añadiendo\(40 \: \text{mL}\) de etanol a\(20 \: \text{mL}\) de agua, el porcentaje en volumen es:
\[\begin{align} \text{Percent by volume} &= \frac{\text{volume of solute}}{\text{volume of solution}} \times 100\% \\ &= \frac{40 \: \text{mL ethanol}}{240 \: \text{mL solution}} \times 100\% \\ &= 16.7\% \: \text{ethanol} \end{align} \nonumber \]
Con frecuencia, las etiquetas de ingredientes en los productos alimenticios y medicamentos tienen cantidades listadas como porcentajes (vea la figura a continuación).
Porcentaje por Masa
El porcentaje masa/masa (% m/m) se define como la masa de un soluto dividida por la masa de una solución por 100:
\[\mathrm{\% \:m/m = \dfrac{mass\: of\: solute}{mass\: of\: solution}\times100\%} \nonumber \]
masa de solución = masa de soluto + masa disolvente
Si puedes medir las masas del soluto y la solución, determinar el porcentaje masa/masa es fácil. Cada masa debe expresarse en las mismas unidades para determinar la concentración adecuada.
Supongamos que se preparó una solución disolviendo\(25.0 \: \text{g}\) el azúcar en\(100.0 \: \text{g}\) agua.
La masa de la solución es
masa de solución = 25.0g azúcar + 100.0g agua = 125.0 g
El porcentaje en masa se calcularía por:
\[\text{Percent by mass} = \frac{25.0 \: \text{g sugar}}{125.0 \: \text{g solution}} \times 100\% = 20.0\% \: \text{sugar} \nonumber \]
Una solución salina con una masa de 355 g tiene 36.5 g de NaCl disueltos en ella. ¿Cuál es la concentración de porcentaje masa/masa de la solución?
Solución
Podemos sustituir las cantidades dadas en la ecuación por porcentaje masa/masa:
\(\mathrm{\%\: m/m=\dfrac{36.5\: g}{355\: g}\times100\%=10.3\%}\)
Una solución de dextrosa (también llamada D-glucosa, C 6 H 12 O 6) con una masa de 2.00 × 10 2 g tiene 15.8 g de dextrosa disueltos en ella. ¿Cuál es la concentración de porcentaje masa/masa de la solución?
- Contestar
-
7.90%
Uso del porcentaje de masa en los cálculos
A veces es posible que desee formar una masa particular de solución de un porcentaje dado en masa y necesite calcular qué masa del soluto usar. Usar el porcentaje de masa como conversión puede ser útil en este tipo de problemas. El porcentaje de masa se puede expresar como un factor de conversión en la forma\(\frac{g \; \rm{solute}}{100 \; \rm{g solution}}\) o\(\frac{100 \; \rm g solution}{g\; \rm{solute}}\)
Por ejemplo, si necesitas hacer una\(5.00\%\) solución\(3000.0 \: \text{g}\) de cloruro de sodio, es necesario determinar la masa de soluto.
Solución
Dado: 3000.0 g de solución de NaCl
Solución de NaCl al 5.00%
Encuentra: masa de soluto =? g NaCl
Otras cantidades conocidas: 5.00 g de NaCl es a 100 g de solución
El factor de conversión apropiado (basado en el porcentaje de masa dado) se puede utilizar a continuación:
Para resolver la masa de NaCl, la masa dada de solución se multiplica por el factor de conversión.
\[g NaCl = 3,000.0 \cancel{g \: NaCl \:solution} \times \frac{5.00 \:g \: NaCl}{100\cancel{g \: NaCl \: solution}} = 150.0g \: NaCl \nonumber \]
Tendrías que\(150 \: \text{g}\) pesar\(\ce{NaCl}\) y agregarlo a\(2850 \: \text{g}\) de agua. Observe que fue necesario restar la masa del\(\ce{NaCl}\)\(\left( 150 \: \text{g} \right)\) de la masa de solución\(\left( 3000 \: \text{g} \right)\) para calcular la masa del agua que habría que agregar.
¿Cuál es la cantidad (en g) de peróxido de hidrógeno (H 2 O 2) necesaria para hacer una solución de 6.00 kg, 3.00% (en masa) H 2 O 2?
Contestar
180. g H 2 O 2
Resumen
- Las soluciones están compuestas por un disolvente (componente principal) y un soluto (componente menor).
- La concentración de soluciones se puede expresar con mayor precisión en términos de molaridad, porcentaje en volumen y porcentaje en masa.
Colaboradores y Atribuciones
CK-12 Foundation by Sharon Bewick, Richard Parsons, Therese Forsythe, Shonna Robinson, and Jean Dupon.
Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)
Henry Agnew (UC Davis)