4.8E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 51698

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

La práctica hace a la perfección

Determinar si un par ordenado es una solución de un sistema de desigualdades lineales

En los siguientes ejercicios, determine si cada par ordenado es una solución al sistema.

1. $\left\{\begin{array} {l} 3x+y>5\\2x−y\leq 10\end{array}\right.$

ⓐ $(3,−3)$
ⓑ $(7,1)$

2. $\left\{\begin{array} {l} 4x−y<10\\−2x+2y>−8\end{array}\right.$

ⓐ $(5,−2)$
ⓑ $(−1,3)$

Contestar: ⓐ falso ⓑ verdadero

3. $\left\{\begin{array} {l} y>\frac{2}{3}x−5\\x+\frac{1}{2}y\leq 4\end{array}\right.$

ⓐ $(6, −4)$
ⓑ $(3, 0)$

4. $\left\{\begin{array} {l} y<\frac{3}{2}x+3\\ \frac{3}{4}x−2y<5\end{array}\right.$

ⓐ $(−4,−1)$
ⓑ $(8, 3)$

Contestar: ⓐ falso ⓑ verdadero

5. $\left\{\begin{array} {l} 7x+2y>14\\5x−y\leq 8\end{array}\right.$

ⓐ $(2, 3)$
ⓑ $(7, −1)$

6. $\left\{\begin{array} {l} 6x−5y<20\\−2x+7y>−8 \end{array}\right.$

ⓐ $(1, −3)$
ⓑ $(−4, 4)$

Contestar: ⓐ falso ⓑ verdadero

Resolver un sistema de desigualdades lineales mediante gráficos

En los siguientes ejercicios, resuelve cada sistema graficando.

7. $\left\{\begin{array} {l} y\leq 3x+2\\y>x−1\end{array}\right.$

8. $\left\{\begin{array} {l} y<−2x+2\\y\geq −x−1\end{array}\right.$

Contestar

La figura muestra la gráfica de desigualdades y menor que menos dos veces x más dos e y mayor o igual a menos x menos uno. Se muestran dos líneas que se cruzan, una en rojo y la otra en azul. El área ligada por las dos líneas se muestra en gris.

La solución es la región gris.

9. $\left\{\begin{array} {l} y<2x−1\\y\leq −\frac{1}{2}x+4\end{array}\right.$

10. $\left\{\begin{array} {l} y\geq −\frac{2}{3}x+2\\y>2x−3\end{array}\right.$

Contestar

En la figura se muestra la gráfica de las desigualdades y mayores o iguales a menos dos por tres x más dos e y mayores que dos por x menos tres. Se muestran dos líneas que se cruzan, una en rojo y la otra en azul. La región ligada por ellos se muestra en gris.

La solución es la región gris.

11. $\left\{\begin{array} {l} x−y>1\\y<−\frac{1}{4}x+3\end{array}\right.$

12. $\left\{\begin{array} {l} x+2y<4\\y<x−2\end{array}\right.$

Contestar

En la figura se muestra la gráfica de las desigualdades x menos dos veces y menos de cuatro e y menos de x menos dos. Se muestran dos líneas que se cruzan, una en azul y la otra en rojo. El área ligada por las líneas se muestra en gris.

La solución es la región gris.

13. $\left\{\begin{array} {l} 3x−y\geq 6\\y\geq −\frac{1}{2}x\end{array}\right.$

14. $\left\{\begin{array} {l} x+4y\geq 8\\y\leq \frac{3}{4}x\end{array}\right.$

Contestar

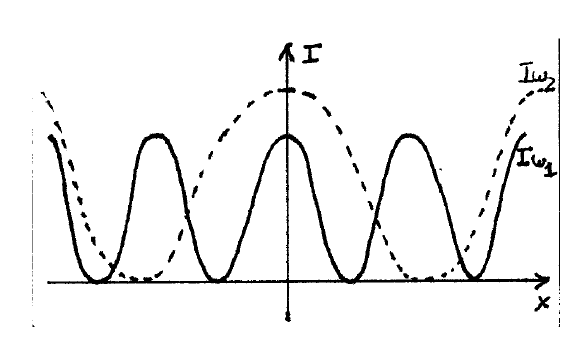
La figura muestra la gráfica de las desigualdades dos veces x más cuatro veces y mayor o igual a ocho e y menor o igual a menos tres cuartas partes de x Se muestran dos líneas que se cruzan, una en azul y la otra en rojo. El área ligada por las líneas se muestra en gris. Es la solución.

La solución es la región gris.

15. $\left\{\begin{array} {l} 2x−5y<10\\3x+4y\geq 12\end{array}\right.$

16. $\left\{\begin{array} {l} 3x−2y\leq 6\\−4x−2y>8\end{array}\right.$

Contestar

La figura muestra la gráfica de las desigualdades tres veces x menos dos veces y menor o igual a seis y menos cuatro veces x menos dos veces y mayor que ocho. Se muestran dos líneas que se cruzan, una en azul y la otra en rojo. El área ligada por las líneas se muestra en gris. Es la solución.

La solución es la región gris.

17. $\left\{\begin{array} {l} 2x+2y>−4\\−x+3y\geq 9\end{array}\right.$

18. $\left\{\begin{array} {l} 2x+y>−6\\−x+2y\geq −4\end{array}\right.$

Contestar

La figura muestra la gráfica de las desigualdades dos veces x más y mayor que menos seis y menos x más dos veces y mayor o igual a menos cuatro. Se muestran dos líneas que se cruzan, una en azul y la otra en rojo. El área ligada por las líneas se muestra en gris. Es la solución.

La solución es la región gris.

19. $\left\{\begin{array} {l} x−2y<3\\y\leq 1\end{array}\right.$

20. $\left\{\begin{array} {l} x−3y>4\\y\leq −1\end{array}\right.$

Contestar

En la figura se muestra la gráfica de las desigualdades x menos tres veces y mayor que cuatro e y menor o igual a menos uno. Se muestran dos líneas que se cruzan, una en azul y la otra en rojo. El área ligada por las líneas se muestra en gris. Es la solución.

La solución es la región gris.

21. $\left\{\begin{array} {l} y\geq −\frac{1}{2}x−3\\x\leq 2\end{array}\right.$

22. $\left\{\begin{array} {l} y\leq −\frac{2}{3}x+5\\x\geq 3\end{array}\right.$

Contestar

En la figura se muestra la gráfica de la desigualdad y menor o igual a menos dos por tres veces x más cinco y x mayor o igual a tres. Se muestran dos líneas que se cruzan, una en azul y la otra en rojo. El área ligada por las líneas se muestra en gris. Es la solución.

La solución es la región gris.

23. $\left\{\begin{array} {l} y\geq \frac{3}{4}x−2\\y<2\end{array}\right.$

24. $\left\{\begin{array} {l} y\leq −\frac{1}{2}x+3\\y<1\end{array}\right.$

Contestar

En la figura se muestra la gráfica de las desigualdades y menores o iguales a menos la mitad x más tres e y menos de uno. Se muestran dos líneas que se cruzan, una en azul y la otra en rojo. El área ligada por las líneas se muestra en gris. Es la solución.

La solución es la región gris.

25. $\left\{\begin{array} {l} 3x−4y<8\\x<1\end{array}\right.$

26. $\left\{\begin{array} {l} −3x+5y>10\\x>−1\end{array}\right.$

Contestar

La figura muestra la gráfica de las desigualdades menos tres veces x más cinco veces y mayor que diez y x mayor que menos uno. Se muestran dos líneas que se cruzan, una en azul y la otra en rojo. El área ligada por las líneas se muestra en gris. Es la solución.

La solución es la región gris.

27. $\left\{\begin{array} {l} x\geq 3\\y\leq 2\end{array}\right.$

28. $\left\{\begin{array} {l} x\leq −1\\y\geq 3\end{array}\right.$

Contestar

En la figura se muestra la gráfica de las desigualdades x menor o igual a menos uno y y mayor o igual que tres. Se muestran dos líneas que se cruzan, una en azul y la otra en rojo. El área ligada por las líneas se muestra en gris. Es la solución.

La solución es la región gris.

29. $\left\{\begin{array} {l} 2x+4y>4 \\ y\leq −\frac{1}{2}x−2\end{array}\right.$

30. $\left\{\begin{array} {l} x−3y\geq 6\\y>\frac{1}{3}x+1\end{array}\right.$

Contestar

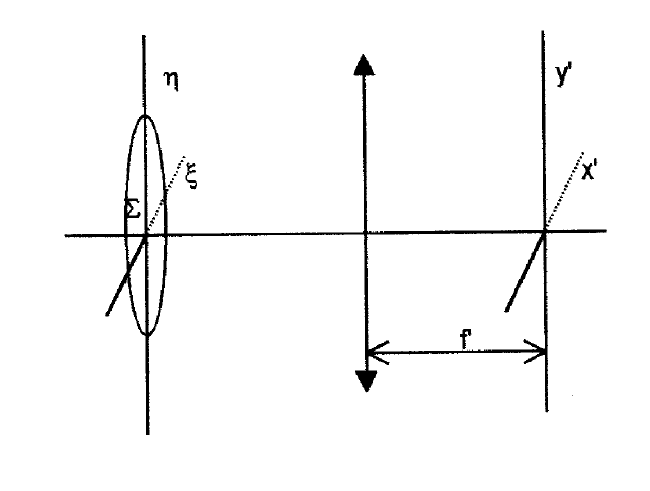
En la figura se muestra la gráfica de las desigualdades x menos tres veces y mayor o igual a seis y y mayor que un tercio de x más uno. Se muestran dos líneas no intersecantes, una en azul y la otra en rojo.

No hay solución.

31. $\left\{\begin{array} {l} −2x+6y<0\\6y>2x+4\end{array}\right.$

32. $\left\{\begin{array} {l} −3x+6y>12\\4y\leq 2x−4\end{array}\right.$

Contestar

No hay solución.

33. $\left\{\begin{array} {l} y\geq −3x+2\\3x+y>5\end{array}\right.$

34. $\left\{\begin{array} {l} y\geq \frac{1}{2}x−1\\−2x+4y\geq 4\end{array}\right.$

Contestar

La figura muestra la gráfica de las desigualdades y mayor o igual a menos mitad x menos uno y menos dos veces x más cuatro veces y mayor o igual a cuatro. Se muestran dos líneas no intersecantes, una en azul y la otra en rojo. El área de solución se muestra en gris.

La solución es la región gris.

35. $\left\{\begin{array} {l} y\leq −\frac{1}{4}x−2\\x+4y<6\end{array}\right.$

36. $\left\{\begin{array} {l} y\geq 3x−1\\−3x+y>−4\end{array}\right.$

Contestar

La figura muestra la gráfica de las desigualdades y mayores o iguales a tres veces x menos uno y menos tres veces x más y mayor que menos cuatro. Se muestran dos líneas no intersecantes, una en azul y la otra en rojo. El área de solución se muestra en gris.

La solución es la región gris.

37. $\left\{\begin{array} {l} 3y>x+2\\−2x+6y>8\end{array}\right.$

38. $\left\{\begin{array} {l} y<\frac{3}{4}x−2\\−3x+4y<7\end{array}\right.$

Contestar

La solución es la región gris.

Resolver Aplicaciones de Sistemas de Desigualdades

En los siguientes ejercicios, traducir a un sistema de desigualdades y resolver.

39. Caitlyn vende sus dibujos en la feria del condado. Ella quiere vender al menos 60 dibujos y tiene retratos y paisajes. Ella vende los retratos por 15 dólares y los paisajes por 10 dólares. Ella necesita vender por lo menos $800 en dibujos con el fin de obtener una ganancia.

ⓐ Escribir un sistema de desigualdades para modelar esta situación.
ⓑ Grafica el sistema.
ⓒ ¿Obtendrá ganancias si vende 20 retratos y 35 paisajes?
ⓓ ¿Obtendrá ganancias si vende 50 retratos y 20 paisajes?

40. Jake no quiere gastar más de 50 dólares en bolsas de fertilizante y turba musgo para su jardín. El fertilizante cuesta $2 la bolsa y el musgo de turba cuesta $5 la bolsa. La camioneta de Jake puede contener como máximo 20 bolsas.

ⓐ Escribir un sistema de desigualdades para modelar esta situación.
ⓑ Grafica el sistema.
ⓒ ¿Puede comprar 15 bolsas de fertilizante y 4 bolsas de turba musgo?
ⓓ ¿Puede comprar 10 bolsas de fertilizante y 10 bolsas de turba musgo?

Contestar

ⓐ $\left\{\begin{array} {l} f\geq 0 \\ p\geq 0 \\ f+p\leq 202 \\ f+5p\leq 50\end{array}\right.$
ⓑ

La figura muestra la gráfica de las desigualdades f más p menor o igual a veinte y dos f y cinco p menor o igual a cincuenta. Se muestran dos líneas que se cruzan, una en azul y la otra en rojo. Se muestra un área en gris.

ⓒ sí
ⓓ no

41. Reiko necesita enviar por correo sus tarjetas y paquetes de Navidad y quiere mantener sus costos de correo a no más de $500. El número de tarjetas es al menos 4 más del doble del número de paquetes. El costo de enviar una tarjeta (con fotos adjuntas) es de $3 y para un paquete el costo es de $7.

ⓐ Escribir un sistema de desigualdades para modelar esta situación.
ⓑ Grafica el sistema.
ⓒ ¿Puede enviar 60 tarjetas y 26 paquetes?
ⓓ ¿Puede enviar 90 tarjetas y 40 paquetes?

42. Juan está estudiando para sus exámenes finales en química y álgebra. sabe que sólo tiene 24 horas para estudiar, y le tomará al menos tres veces más tiempo estudiar para álgebra que química.

ⓐ Escribir un sistema de desigualdades para modelar esta situación.
ⓑ Grafica el sistema.
ⓒ ¿Puede pasar 4 horas en química y 20 horas en álgebra?
ⓓ ¿Puede pasar 6 horas en química y 18 horas en álgebra?

Contestar

ⓐ $\left\{\begin{array} {l} c\geq 0\\a\geq 0\\c+a\leq 24\\a\geq 3c\end{array}\right.$
ⓑ

En la figura se muestra la gráfica de las desigualdades c más una menor o igual a veinticuatro y una mayor o igual a tres veces c. Se muestran dos líneas que se cruzan, una en azul y la otra en rojo. Se muestra un área en gris.

ⓒ sí
ⓓ no

43. Jocelyn está embarazada y por lo que necesita comer al menos 500 calorías más al día de lo habitual. Al comprar abarrotes un día con un presupuesto de 15 dólares para el alimento extra, compra plátanos que tienen 90 calorías cada uno y barras de granola de chocolate que tienen 150 calorías cada una. El plátano costó $0.35 cada uno y las barras de granola cuestan $2.50 cada una.

ⓐ Escribir un sistema de desigualdades para modelar esta situación.
ⓑ Grafica el sistema.
ⓒ ¿Podría comprar 5 plátanos y 6 barras de granola?
ⓓ ¿Podría comprar 3 plátanos y 4 barras de granola?

44. Mark está tratando de construir masa muscular y por lo que necesita comer al menos 80 gramos adicionales de proteína al día. Una botella de agua proteica cuesta $3.20 y una barra de proteína cuesta $1.75. El agua proteica suministra 27 gramos de proteína y la barra suministra 16 gramos. Si tiene $10 dólares para gastar

ⓐ Escribir un sistema de desigualdades para modelar esta situación.
ⓑ Grafica el sistema.
ⓒ ¿Podría comprar 3 botellas de agua proteica y 1 barra de proteína?
ⓓ ¿No podría comprar botellas de agua proteica y 5 barras de proteína?

Contestar

ⓐ $\left\{\begin{array} {l} w\geq 0\\b\geq 0\\27w+16b>80\\3.20w+1.75b\leq 10\end{array}\right.$
ⓑ

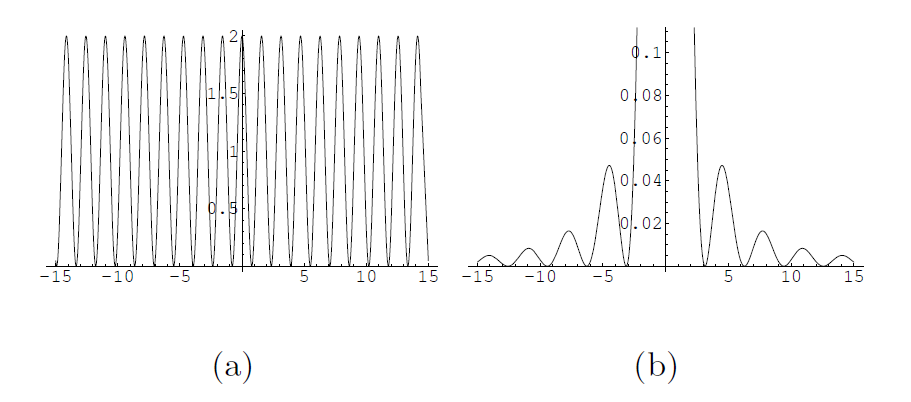
La figura muestra la gráfica de las desigualdades veintisiete veces w más dieciséis veces b mayor que ochenta y tres puntos dos por w más un punto siete cinco b menor o igual a diez. Se muestran dos líneas que se cruzan, una en azul y la otra en rojo. Se muestra un área en gris.

ⓒ no
ⓓ sí

45. Jocelyn desea aumentar tanto su consumo de proteínas como su aporte calórico. Ella desea tener al menos 35 gramos más de proteína cada día y no más de 200 calorías adicionales diarias. Una onza de queso cheddar tiene 7 gramos de proteína y 110 calorías. Una onza de queso parmesano tiene 11 gramos de proteína y 22 calorías.

ⓐ Escribir un sistema de desigualdades para modelar esta situación.
ⓑ Grafica el sistema.
ⓒ ¿Podría comer 1 onza de queso cheddar y 3 onzas de queso parmesano?
ⓓ ¿Podría comer 2 onzas de queso cheddar y 1 onza de queso parmesano?

46. Mark está aumentando su rutina de ejercicios al correr y caminar al menos 4 millas cada día. Su objetivo es quemar un mínimo de 1500 calorías de este ejercicio. Caminar quema 270 calorías/milla y correr quema 650 calorías.

ⓐ Escribir un sistema de desigualdades para modelar esta situación.
ⓑ Grafica el sistema.
ⓒ ¿Podría cumplir su objetivo caminando 3 millas y corriendo 1 milla?
ⓓ ¿Podría su meta caminando 2 millas y corriendo 2 millas

Contestar

ⓐ $\left\{\begin{array} {l} w\geq 0\\r\geq 0\\w+r\geq 4\\270w+650r\geq 1500\end{array}\right.$
ⓑ

ⓒ no
ⓓ sí

Ejercicios de escritura

47. Gráfica la desigualdad $x−y\geq 3$. ¿Cómo sabes qué lado de la línea se $x−y=3$ debe sombrear?

48. Grafica el sistema $\left\{\begin{array} {l} x+2y\leq 6 \\ y\geq −\frac{1}{2}x−4\end{array}\right.$. ¿Qué significa la solución?

Contestar: Las respuestas variarán.

Autocomprobación

ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.

En la figura se muestra una tabla con cuatro columnas y cuatro filas. La primera fila es la fila del título. Los cuatro títulos son que puedo..., con confianza, con algo de ayuda y No — ¡No lo consigo! En la segunda fila de la primera columna, el texto dice 'determinar si un par ordenado es una solución de un sistema de desigualdades lineales'. En la tercera fila de la primera columna, el texto dice 'resolver aplicaciones de sistemas de desigualdades. '

ⓑ ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?

Search

Text Color

Text Size

Margin Size

Font Type