7.3: Sumar y restar expresiones racionales
- Page ID
- 51809
Al final de esta sección, usted será capaz de:
- Sumar y restar expresiones racionales con un denominador común
- Sumar y restar expresiones racionales cuyos denominadores son opuestos
- Encontrar el mínimo denominador común de las expresiones racionales
- Sumar y restar expresiones racionales con denominadores diferentes
- Suma y resta funciones racionales
Sumar y restar expresiones racionales con un denominador común
¿Cuál es el primer paso que das al agregar fracciones numéricas? Se comprueba si tienen un denominador común. Si lo hacen, se agregan los numeradores y se coloca la suma sobre el denominador común. Si no tienen un denominador común, encuentras uno antes de agregar.
Es lo mismo con las expresiones racionales. Para sumar expresiones racionales, deben tener un denominador común. Cuando los denominadores son iguales, se agregan los numeradores y se coloca la suma sobre el denominador común.
Si \(p\), \(q\), y \(r\) son polinomios donde \(r\neq 0\), entonces
\[\dfrac{p}{r}+\dfrac{q}{r}=\dfrac{p+q}{r} \quad \text{and} \quad \dfrac{p}{r}−\dfrac{q}{r}=\dfrac{p−q}{r}\nonumber\]
Para sumar o restar expresiones racionales con un denominador común, sumar o restar los numeradores y colocar el resultado sobre el denominador común.
Siempre simplificamos expresiones racionales. Asegúrate de tener en cuenta, si es posible, después de restar los numeradores para que puedas identificar cualquier factor común.
Recuerden, también, que no permitimos valores que harían el denominador cero. ¿De qué valor \(x\) debe excluirse en el siguiente ejemplo?
Añadir: \(\dfrac{11x+28}{x+4}+\dfrac{x^2}{x+4}\).
Solución
Ya que el denominador es \(x+4\), debemos excluir el valor \(x=−4\).
\(\begin{array} {ll} &\dfrac{11x+28}{x+4}+\dfrac{x^2}{x+4},\space x\neq −4 \\ \begin{array} {l} \text{The fractions have a common denominator,} \\ \text{so add the numerators and place the sum} \\ \text{over the common denominator.} \end{array} &\dfrac{11x+28+x^2}{x+4} \\ & \\ \text{Write the degrees in descending order.} &\dfrac{x^2+11x+28}{x+4} \\ & \\ \text{Factor the numerator.} &\dfrac{(x+4)(x+7)}{x+4} \\ & \\ \text{Simplify by removing common factors.} &\dfrac{\cancel{(x+4)}(x+7)}{\cancel{x+4}} \\ & \\ \text{Simplify.} &x+7 \end{array}\)
La expresión simplifica a \(x+7\) pero la expresión original tenía un denominador de \(x+4\) eso \(x\neq −4\).
Simplificar: \(\dfrac{9x+14}{x+7}+\dfrac{x^2}{x+7}\).
- Responder
-
\(x+2\)
Simplificar: \(\dfrac{x^2+8x}{x+5}+\dfrac{15}{x+5}\).
- Responder
-
\(x+3\)
Para restar expresiones racionales, también deben tener un denominador común. Cuando los denominadores son iguales, restas los numeradores y colocas la diferencia sobre el denominador común. Ten cuidado con los signos al restar un binomio o trinomio.
Restar: \(\dfrac{5x^2−7x+3}{x^2−3x+18}−\dfrac{4x^2+x−9}{x^2−3x+18}\).
Solución
\(\begin{array} {ll} &\dfrac{5x^2−7x+3}{x^2−3x+18}−\dfrac{4x^2+x−9}{x^2−3x+18} \\ & \\ \begin{array} {l} \text{Subtract the numerators and place the} \\ \text{difference over the common denominator.} \end{array} &\dfrac{5x^2−7x+3−(4x^2+x−9)}{x^2−3x+18} \\ & \\ \text{Distribute the sign in the numerator.} &\dfrac{5x^2−7x+3−4x^2−x+9}{x^2−3x−18} \\ & \\ \text{Combine like terms.} &\dfrac{x^2−8x+12}{x^2−3x−18} \\ & \\ \text{Factor the numerator and the denominator.} &\dfrac{(x−2)(x−6)}{(x+3)(x−6)} \\ & \\ \text{Simplify by removing common factors.} &\dfrac{(x−2)\cancel{(x−6)}}{(x+3)\cancel{(x−6)}} \\ & \\ &(x−2)(x+3) \end{array}\)
Restar: \(\dfrac{4x^2−11x+8}{x^2−3x+2}−\dfrac{3x^2+x−3}{x^2−3x+2}\).
- Responder
-
\(\dfrac{x−11}{x−2}\)
Restar: \(\dfrac{6x^2−x+20}{x^2−81}−\dfrac{5x^2+11x−7}{x^2−81}\).
- Responder
-
\(\dfrac{x−3}{x+9}\)
Sumar y restar expresiones racionales cuyos denominadores son opuestos
Cuando los denominadores de dos expresiones racionales son opuestos, es fácil obtener un denominador común. Sólo tenemos que multiplicar una de las fracciones por \(\dfrac{−1}{−1}\).
Veamos cómo funciona esto.
| Multiplica la segunda fracción por \(\dfrac{−1}{−1}\). |  |
| Los denominadores son los mismos. | 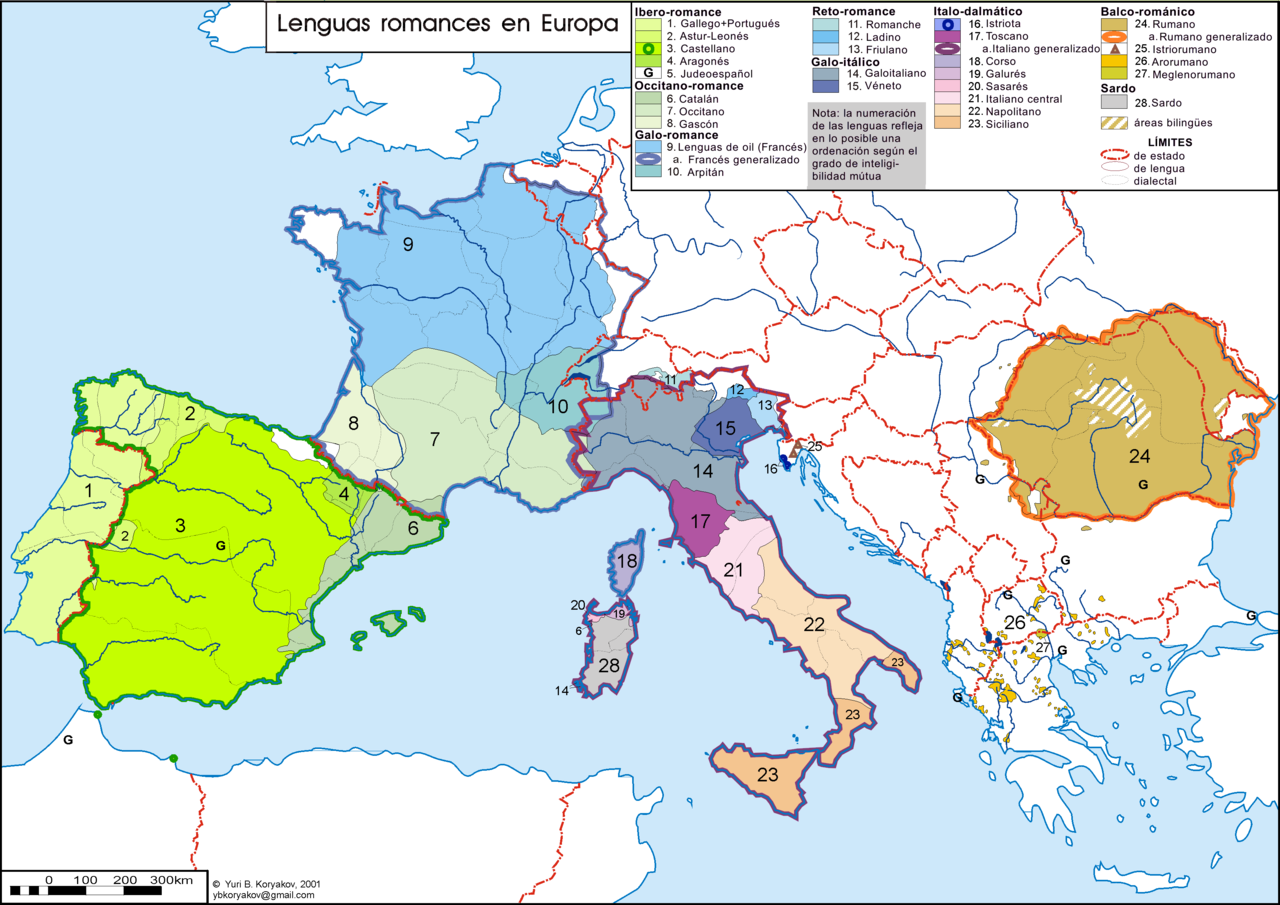 |
| Simplificar. |
Ten cuidado con los signos mientras trabajas con los opuestos cuando se restan las fracciones.
Restar: \(\dfrac{m^2−6m}{m^2−1}−\dfrac{3m+2}{1−m^2}\).
Solución
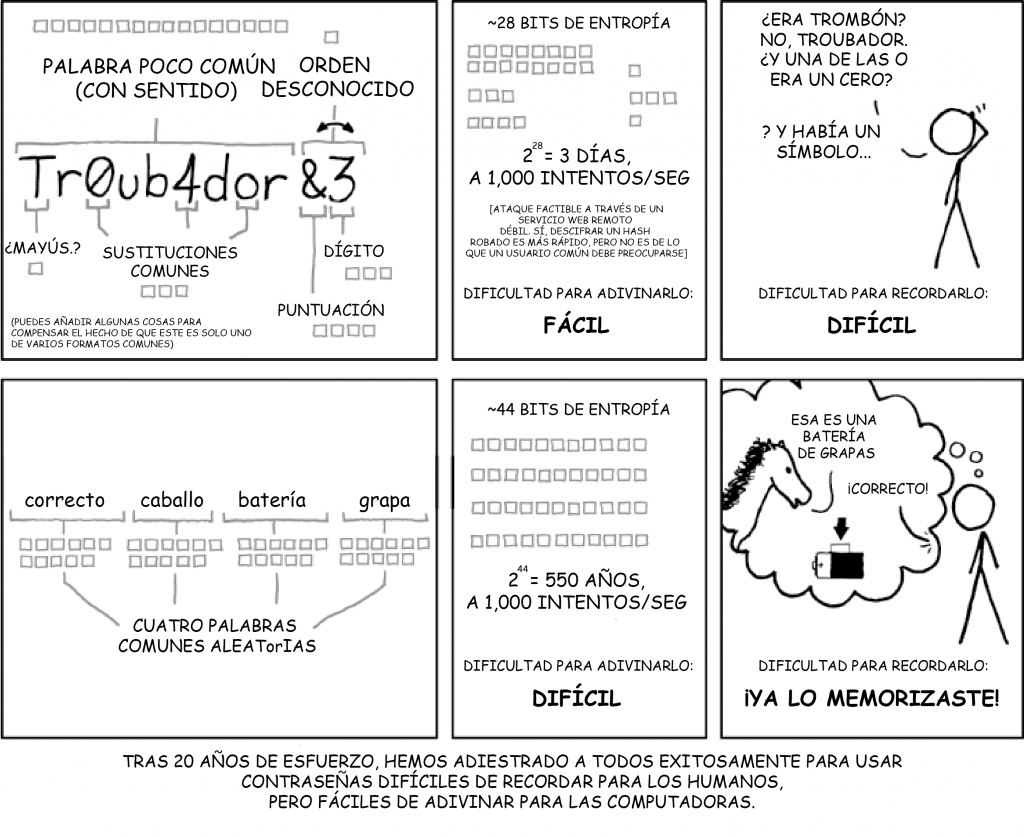 |
|
|
Los denominadores son opuestos, así que multiplica la |
 |
| Simplifica la segunda fracción. | 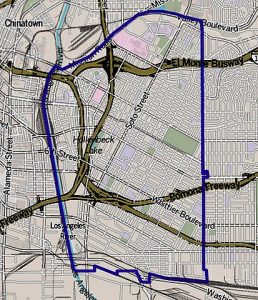 |
| Los denominadores son los mismos. Restar los numeradores. | |
| Distribuir. | |
| Combina términos similares. | 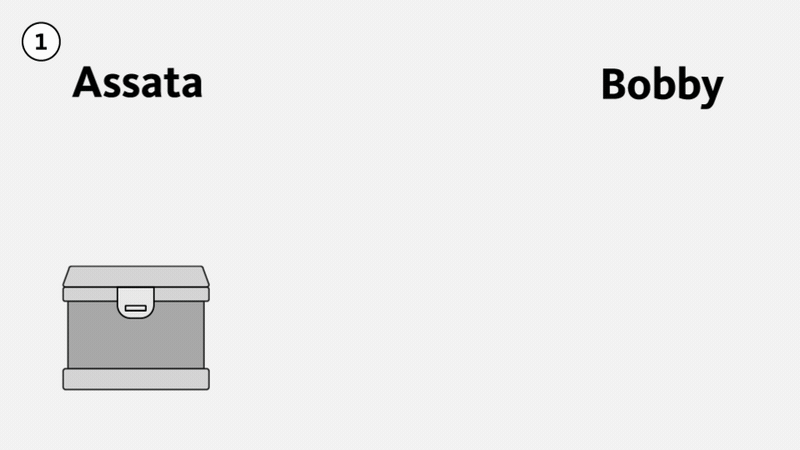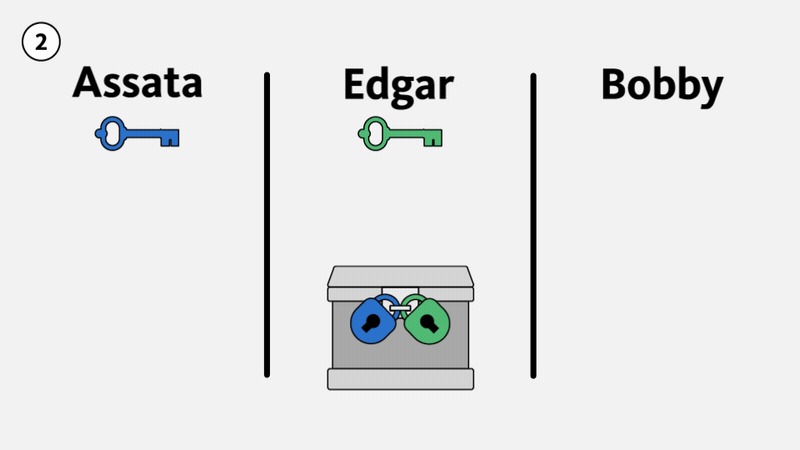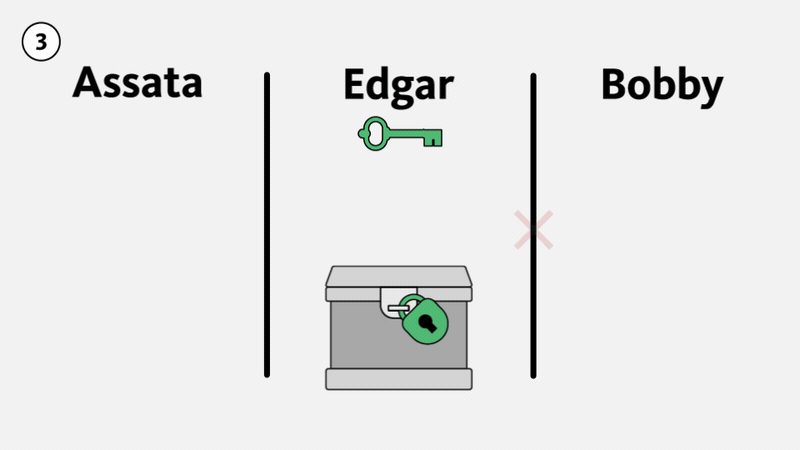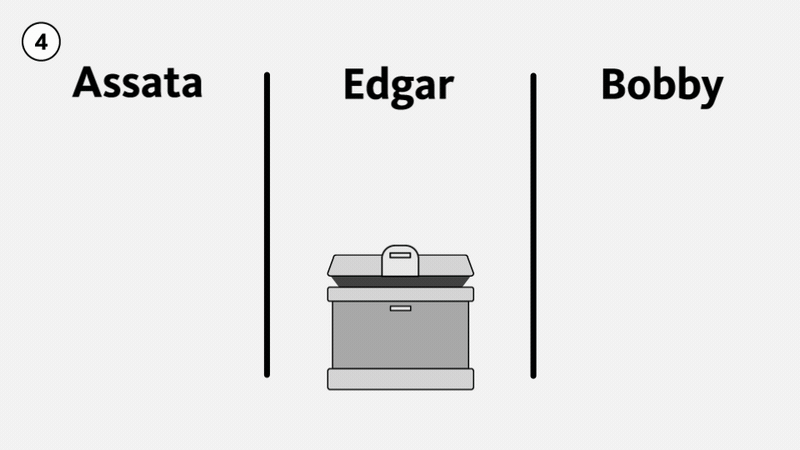 |
| Factor el numerador y el denominador. | |
| Simplifique eliminando factores comunes. | |
| Simplificar. |
Restar: \(\dfrac{y^2−5y}{y^2−4}−\dfrac{6y−6}{4−y^2}\).
- Responder
-
\(\dfrac{y+3}{y+2}\)
Restar: \(\dfrac{2n^2+8n−1}{n^2−1}−\dfrac{n^2−7n−1}{1−n^2}\).
- Responder
-
\(\dfrac{3n−2}{n−1}\)
Encuentre el denominador menos común de las expresiones racionales
Cuando sumemos o restemos expresiones racionales con denominadores diferentes, necesitaremos obtener denominadores comunes. Si revisamos el procedimiento que utilizamos con fracciones numéricas, sabremos qué hacer con las expresiones racionales.
Veamos este ejemplo: \(\dfrac{7}{12}+\dfrac{5}{18}\). Dado que los denominadores no son los mismos, el primer paso fue encontrar el menos común denominador (LCD).
Para encontrar el LCD de las fracciones, factorizamos 12 y 18 en números primos, alineando cualquier primos comunes en columnas. Después “derribamos” un primo de cada columna. Finalmente, multiplicamos los factores para encontrar el LCD.
Cuando agregamos fracciones numéricas, una vez que encontramos el LCD, reescribimos cada fracción como fracción equivalente con la LCD multiplicando el numerador y el denominador por el mismo número. Ya estamos listos para sumar.
Hacemos lo mismo para las expresiones racionales. Sin embargo, dejamos el LCD en forma factorizada.
- Factor cada denominador por completo.
- Enumerar los factores de cada denominador. Haga coincidir los factores verticalmente cuando sea posible.
- Derriba las columnas incluyendo todos los factores, pero no incluya los factores comunes dos veces.
- Escribir el LCD como el producto de los factores.
Recuerda, siempre excluimos valores que harían el denominador cero. ¿Qué valores de xx debemos excluir en este siguiente ejemplo?
a. Encontrar el LCD para las expresiones \(\dfrac{8}{x^2−2x−3}\), \(\dfrac{3x}{x^2+4x+3}\) y b. reescribirlas como expresiones racionales equivalentes con el mínimo común denominador.
Solución
a.
| Encuentra la pantalla LCD para \(\dfrac{8}{x^2−2x−3}\), \(\dfrac{3x}{x^2+4x+3}\). | |
| Factor cada denominador por completo, alineando factores comunes. Bajen las columnas. |
|
| Escribir el LCD como el producto de los factores. |
b.
| Factor cada denominador. | |
| Multiplica cada denominador por el factor LCD 'faltante' y multiplica cada numerador por el mismo factor. |
|
| Simplifica los numeradores. |
a. Encontrar el LCD para las expresiones \(\dfrac{2}{x^2−x−12}\), \(\dfrac{1}{x^2−16}\) b. reescribirlas como expresiones racionales equivalentes con el mínimo común denominador.
- Responder
-
a. \((x−4)(x+3)(x+4)\)
b. \(\dfrac{2x+8}{(x−4)(x+3)(x+4)}\),
\(\dfrac{x+3}{(x−4)(x+3)(x+4)}\)
a. Encontrar el LCD para las expresiones \(\dfrac{3x}{x^2−3x+10}\), \(\dfrac{5}{x^2+3x+2}\) b. reescribirlas como expresiones racionales equivalentes con el mínimo común denominador.
- Responder
-
a. \((x+2)(x−5)(x+1)\)
b. \(\dfrac{3x^2+3x}{(x+2)(x−5)(x+1)}\),
\(\dfrac{5x−25}{(x+2)(x−5)(x+1)}\)
Sumar y restar expresiones racionales con denominadores diferentes
Ahora tenemos todos los pasos que necesitamos para sumar o restar expresiones racionales con denominadores distintos.
Añadir: \(\dfrac{3}{x−3}+\dfrac{2}{x−2}\).
Solución
Añadir: \(\dfrac{2}{x−2}+\dfrac{5}{x+3}\).
- Responder
-
\(\dfrac{7x−4}{(x−2)(x+3)}\)
Añadir: \(\dfrac{4}{m+3}+\dfrac{3}{m+4}\).
- Responder
-
\(\dfrac{7m+25}{(m+3)(m+4)}\)
Los pasos utilizados para agregar expresiones racionales se resumen aquí.
- Determina si las expresiones tienen un denominador común.
- Sí — ve al paso 2.
- No — Reescribe cada expresión racional con la pantalla LCD.
- Encuentra la pantalla LCD.
- Reescribe cada expresión racional como una expresión racional equivalente con el LCD.
- Sumar o restar las expresiones racionales.
- Simplificar, si es posible.
Evita la tentación de simplificar demasiado pronto. En el ejemplo anterior, debemos dejar la primera expresión racional en cuanto \(\dfrac{3x−6}{(x−3)(x−2)}\) a poder sumarla \(\dfrac{2x−6}{(x−2)(x−3)}\). Simplifique sólo después de haber combinado los numeradores.
Añadir: \(\dfrac{8}{x^2−2x−3}+\dfrac{3x}{x^2+4x+3}\).
Solución
| ¿Las expresiones tienen un denominador común? | No. |
| Reescribe cada expresión con la pantalla LCD. | |
| \(\begin{array} {ll} & \\ & \\ \text{Find the LCD.} &\begin{array} {l} \hspace{5mm} x^2−2x−3=(x+1)(x−3) \\ \underline{x^2+4x+3=(x+1)\quad (x+3)} \\ & \\ \qquad LCD=(x+1)(x−3)(x+3) \end{array} \end{array} \) | |
| Reescribe cada expresión racional como una expresión racional equivalente con el LCD. |
|
| Simplifica los numeradores. | |
| Añadir las expresiones racionales. | |
| Simplifica el numerador. | |
| El numerador es primo, por lo que no hay factores comunes. |
Añadir: \(\dfrac{1}{m^2−m−2}+\dfrac{5m}{m^2+3m+2}\).
- Responder
-
\(\dfrac{5m^2−9m+2}{(m+1)(m−2)(m+2)}\)
Añadir: \(\dfrac{2n}{n^2−3n−10}+\dfrac{6}{n^2+5n+6}\).
- Responder
-
\(\dfrac{2n^2+12n−30}{(n+2)(n−5)(n+3)}\)
El proceso que utilizamos para restar expresiones racionales con diferentes denominadores es el mismo que para sumar. Simplemente hay que tener mucho cuidado con los signos a la hora de restar los numeradores.
Restar: \(\dfrac{8y}{y^2−16}−\dfrac{4}{y−4}\).
Solución
| ¿Las expresiones tienen un denominador común? | No. |
| Reescribe cada expresión con la pantalla LCD. | |
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} y^2−16=(y−4)(y+4) \\ \quad \underline{y−4=y−4} \\ LCD=(y−4)(y+4) \end{array} \end{array} \) | |
| Reescribe cada expresión racional como una expresión racional equivalente con el LCD. |
|
| Simplifica los numeradores. | |
| Restar las expresiones racionales. | |
| Simplifica el numerador. | |
| Factor el numerador para buscar factores comunes. | |
| Eliminar factores comunes | |
| Simplificar. |
Restar: \(\dfrac{2x}{x^2−4}−\dfrac{1}{x+2}\).
- Responder
-
\(\dfrac{1}{x−2}\)
Restar: \(\dfrac{3}{z+3}−\dfrac{6z}{z^2−9}\).
- Responder
-
\(\dfrac{−3}{z−3}\)
En el siguiente ejemplo hay muchos signos negativos. Ten mucho cuidado.
Restar: \(\dfrac{−3n−9}{n^2+n−6}−\dfrac{n+3}{2−n}\).
Solución
| Factor el denominador. | |
| Ya que \(n−2\) y \(2−n\) son opuestos, multiplicaremos la segunda expresión racional por \(\dfrac{−1}{−1}\). |
|
| Simplificar. Recuerda, \(a−(−b)=a+b\). | |
| ¿Las expresiones racionales tienen un denominador común? No. |
|
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} n^2+n−6=(n−2)(n+3) \\ \quad\underline{n−2=(n−2)} \\ LCD=\quad (n−2)(n+3) \end{array} \end{array} \) | |
| Reescribe cada expresión racional como una expresión racional equivalente con el LCD. |
|
| Simplifica los numeradores. | |
| Añadir las expresiones racionales. | |
| Simplifica el numerador. | |
| Factor el numerador para buscar factores comunes. | |
| Simplificar. |
Restar: \(\dfrac{3x−1}{x^2−5x−6}−\dfrac{2}{6−x}\).
- Responder
-
\(\dfrac{5x+1}{(x−6)(x+1)}\)
Restar: \(\dfrac{−2y−2}{y^2+2y−8}−\dfrac{y−1}{2−y}\).
- Responder
-
\(\dfrac{y+3}{y+4}\)
Las cosas pueden ponerse muy desordenadas cuando ambas fracciones deben multiplicarse por un binomio para obtener el denominador común.
Restar: \(\dfrac{4}{a^2+6a+5}−\dfrac{3}{a^2+7a+10}\).
Solución
| Factor los denominadores. | |
| ¿Las expresiones racionales tienen un denominador común? No. |
|
|
\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} a^2+6a+5=(a+1)(a+5) \\ \underline{a^2+7a+10=(a+5)(a+2)} \\ LCD=(a+1)(a+5)(a+2) \end{array} \end{array} \) |
|
| Reescribe cada expresión racional como una expresión racional equivalente con el LCD. |
|
| Simplifica los numeradores. | |
| Restar las expresiones racionales. | |
| Simplifica el numerador. | |
| Busque factores comunes. | |
| Simplificar. |
Restar: \(\dfrac{3}{b^2−4b−5}−\dfrac{2}{b^2−6b+5}\).
- Responder
-
\(\dfrac{1}{(b+1)(b−1)}\)
Restar: \(\dfrac{4}{x^2−4}−\dfrac{3}{x^2−x−2}\).
- Responder
-
\(\dfrac{1}{(x+2)(x+1)}\)
Seguimos los mismos pasos que antes para encontrar el LCD cuando tenemos más de dos expresiones racionales. En el siguiente ejemplo, comenzaremos por factorizar los tres denominadores para encontrar su LCD.
Simplificar: \(\dfrac{2u}{u−1}+\dfrac{1}{u}−\dfrac{2u−1}{u^2−u}\).
Solución
| ¿Las expresiones tienen un denominador común? No. Reescribe cada expresión con la pantalla LCD. |
|
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} u−1=(u−1) \\ u=u \\ \underline{u^2−u=u(u−1)} \\ LCD=u(u−1) \end{array} \end{array}\) | |
| Reescribe cada expresión racional como una expresión racional equivalente con el LCD. |
|
| Escribir como una expresión racional. | |
| Simplificar. | |
| Factor el numerador, y eliminar factores comunes. |
|
| Simplificar. |
Simplificar: \(\dfrac{v}{v+1}+\dfrac{3}{v−1}−\dfrac{6}{v^2−1}\).
- Responder
-
\(\dfrac{v+3}{v+1}\)
Simplificar: \(\dfrac{3w}{w+2}+\dfrac{2}{w+7}−\dfrac{17w+4}{w^2+9w+14}\).
- Responder
-
\(\dfrac{3w}{w+7}\)
Suma y resta funciones racionales
Para sumar o restar funciones racionales, utilizamos las mismas técnicas que usamos para sumar o restar funciones polinómicas.
Encuentra \(R(x)=f(x)−g(x)\) dónde \(f(x)=\dfrac{x+5}{x−2}\) y \(g(x)=\dfrac{5x+18}{x^2−4}\).
- xolución
-
Suplente en las funciones \(f(x)\), \(g(x)\). Factor los denominadores. ¿Las expresiones tienen un denominador común? No.
Reescribe cada expresión con la pantalla LCD.\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} x−2=(x−2) \\ \underline{x^2−4=(x−2)(x+2)} \\ \hspace{4mm} LCD=(x−2)(x+2)\end{array} \end{array}\) Reescribe cada expresión racional como una expresión racional
equivalente con el LCD.Escribir como una expresión racional. Simplificar. Factor el numerador, y eliminar factores
comunes.Simplificar.
Encuentra \(R(x)=f(x)−g(x)\) dónde \(f(x)=\dfrac{x+1}{x+3}\) y \(g(x)=\dfrac{x+17}{x^2−x−12}\).
- Responder
-
\(\dfrac{x−7}{x−4}\)
Encuentra \(R(x)=f(x)+g(x)\) dónde \(f(x)=\dfrac{x−4}{x+3}\) y \(g(x)=\dfrac{4x+6}{x^2−9}\).
- Responder
-
\(\dfrac{x^2−3x+18}{(x+3)(x−3)}\)
Acceda a este recurso en línea para instrucción y práctica adicional con la adición y resta de expresiones racionales.
- Sumar y restar expresiones racionales- a diferencia de denominadores
Conceptos Clave
- Expresión racional Suma y resta
Si \(p\), \(q\), y \(r\) son polinomios donde \(r\neq 0\), entonces
\[\dfrac{p}{r}+\dfrac{q}{r}=\dfrac{p+q}{r} \quad \text{and} \quad \dfrac{p}{r}−\dfrac{q}{r}=\dfrac{p−q}{r}\nonumber\] - Cómo encontrar el mínimo común denominador de las expresiones racionales.
- Factor cada expresión por completo.
- Enumerar los factores de cada expresión. Haga coincidir los factores verticalmente cuando sea posible.
- Bajen las columnas.
- Escribir el LCD como el producto de los factores.
- Cómo sumar o restar expresiones racionales.
- Determina si las expresiones tienen un denominador común.
- Sí — ve al paso 2.
- No — Reescribe cada expresión racional con la pantalla LCD.
- Encuentra la pantalla LCD.
- Reescribe cada expresión racional como una expresión racional equivalente con el LCD.
- Sumar o restar las expresiones racionales.
- Simplificar, si es posible.
- Determina si las expresiones tienen un denominador común.


