1.1: Números y Símbolos

Primero, tenemos que distinguir la diferencia entre números y los símbolos que usamos para representar números. Un número es una cantidad matemática, generalmente correlacionada en electrónica con una cantidad física como voltaje, corriente o resistencia. Hay muchos tipos diferentes de números. Estos son solo algunos tipos, por ejemplo:

Diferentes tipos de números encuentran diferente aplicación en el mundo físico. Los números enteros funcionan bien para contar objetos discretos, como el número de resistencias en un circuito. Los enteros son necesarios cuando se requieren equivalentes negativos de números enteros. Los números irracionales son números que no pueden expresarse exactamente como la relación de dos enteros, y la relación de la circunferencia de un círculo perfecto a su diámetro (π) es un buen ejemplo físico de esto. Las cantidades no enteras de voltaje, corriente y resistencia a las que estamos acostumbrados a tratar en los circuitos de CC se pueden expresar como números reales, ya sea en forma fraccionaria o decimal. Sin embargo, para el análisis de circuitos de CA, los números reales no logran capturar la esencia dual de magnitud y ángulo de fase, por lo que recurrimos al uso de números complejos en forma rectangular o polar.

Si vamos a usar números para entender procesos en el mundo físico, hacer predicciones científicas, o equilibrar nuestras chequeras, debemos tener una manera de denotarlos simbólicamente. En otras palabras, podemos saber cuánto dinero tenemos en nuestra cuenta corriente, pero para llevar un registro de ello necesitamos tener algún sistema elaborado para simbolizar esa cantidad en papel, o en algún otro tipo de forma para el mantenimiento de registros y seguimiento. Hay dos formas básicas en las que podemos hacer esto: analógica y digital. Con representación analógica, la cantidad se simboliza de una manera infinitamente divisible. Con la representación digital, la cantidad se simboliza de una manera que se empaqueta discretamente.

Probablemente ya estés familiarizado con una representación analógica del dinero, y no te diste cuenta por lo que era. ¿Alguna vez has visto un cartel de recaudación de fondos hecho con una imagen de un termómetro en él, donde la altura de la columna roja indicaba la cantidad de dinero recaudado para la causa? Cuanto más dinero recaudado, más alta es la columna de tinta roja en el cartel.

Este es un ejemplo de una representación analógica de un número. No hay límite real de cuán finamente dividida se puede hacer la altura de esa columna para simbolizar la cantidad de dinero en la cuenta. Cambiar la altura de esa columna es algo que se puede hacer sin cambiar la naturaleza esencial de lo que es. La longitud es una cantidad física que se puede dividir tan pequeña como desee, sin límite práctico. La regla de cálculo es un dispositivo mecánico que utiliza la misma cantidad física, longitud, para representar números y para ayudar a realizar operaciones aritméticas con dos o más números a la vez. También es un dispositivo analógico.

Por otro lado, una representación digital de esa misma cifra monetaria, escrita con símbolos estándar (a veces llamados cifrados), se ve así:

A diferencia del cartel del “termómetro” con su columna roja, esos caracteres simbólicos anteriores no pueden dividirse finamente: esa combinación particular de cifrados representa una cantidad y una sola cantidad. Si se agrega más dinero a la cuenta (+ $40.12), se deben usar diferentes símbolos para representar el nuevo saldo ($35,995.50), o al menos los mismos símbolos dispuestos en diferentes patrones. Este es un ejemplo de representación digital. La contraparte de la regla de cálculo (analógica) es también un dispositivo digital: el ábaco, con cuentas que se mueven hacia adelante y hacia atrás sobre varillas para simbolizar cantidades numéricas:

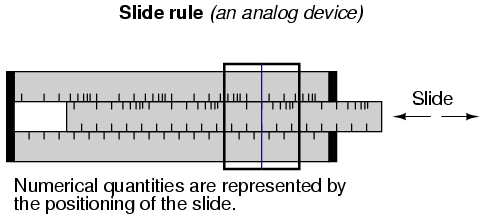
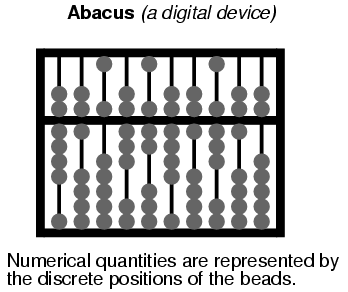
Vamos a contrastar estos dos métodos de representación numérica:

La interpretación de los símbolos numéricos es algo que tendemos a dar por sentado, porque se nos ha enseñado desde hace muchos años. Sin embargo, si trataras de comunicar una cantidad de algo a una persona ignorante de los números decimales, ¡esa persona aún podría entender el sencillo gráfico del termómetro!

Las comparaciones infinitamente divisibles vs. discretas y de precisión son realmente las caras de la misma moneda. El hecho de que la representación digital esté compuesta por símbolos individuales y discretos (dígitos decimales y cuentas de ábaco) necesariamente significa que será capaz de simbolizar cantidades en pasos precisos. Por otro lado, una representación analógica (como la longitud de una regla de cálculo) no está compuesta por pasos individuales, sino más bien un rango de movimiento continuo. La capacidad de una regla de cálculo para caracterizar una cantidad numérica a una resolución infinita es una compensación por imprecisión. Si se choca una regla de cálculo, se introducirá un error en la representación del número que se “ingresó” en ella. Sin embargo, un ábaco debe ser chocado mucho más fuerte antes de que sus cuentas sean completamente desalojadas de sus lugares (suficientes para representar un número diferente).

Por favor, no malinterprete esta diferencia de precisión al pensar que la representación digital es necesariamente más precisa que la analógica. El hecho de que un reloj sea digital no significa que siempre leerá la hora con mayor precisión que un reloj analógico, solo significa que la interpretación de su pantalla es menos ambigua.

La divisibilidad de la representación analógica versus la digital puede iluminarse aún más hablando de la representación de números irracionales. Los números como π se llaman irracionales, porque no pueden expresarse exactamente como la fracción de enteros, o números enteros. Aunque podrías haber aprendido en el pasado que la fracción 22/7 se puede usar para π en los cálculos, esto es solo una aproximación. El número real “pi” no puede expresarse exactamente por ningún número finito o limitado de decimales. Los dígitos de π siguen para siempre:

Es posible, al menos teóricamente, establecer una regla de cálculo (o incluso una columna de termómetro) para representar perfectamente el número π, porque los símbolos analógicos no tienen límite mínimo en el grado en que puedan aumentarse o disminuirse. Si mi regla de cálculo muestra una cifra de 3.141593 en lugar de 3.141592654, puedo chocar la diapositiva un poco más (o menos) para acercarla todavía. Sin embargo, con la representación digital, como con un ábaco, necesitaría varillas adicionales (portaposiciones o dígitos) para representar π con más grados de precisión. Un ábaco con 10 varillas simplemente no puede representar más de 10 dígitos por valor del número π, no importa cómo establezca las cuentas. Para representar perfectamente π, ¡un ábaco tendría que tener un número infinito de cuentas y varillas! La compensación, por supuesto, es la limitación práctica para ajustar y leer símbolos analógicos. Prácticamente hablando, no se puede leer la escala de una regla de cálculo al décimo dígito de precisión, porque las marcas en la escala son demasiado gruesas y la visión humana es demasiado limitada. Un ábaco, por otro lado, se puede fijar y leer sin errores interpretacionales en absoluto.

Además, los símbolos analógicos requieren algún tipo de estándar mediante el cual se puedan comparar para una interpretación precisa. Las reglas de cálculo tienen marcas impresas a lo largo de las diapositivas para traducir la longitud en cantidades estándar. Incluso la tabla del termómetro tiene números escritos a lo largo de su altura para mostrar cuánto dinero (en dólares) representa la columna roja para cualquier cantidad dada de altura. Imagínese si todos intentáramos comunicarnos números simples entre sí espaciando nuestras manos a distancias variables. El número 1 podría significar sosteniendo nuestras manos a una pulgada de distancia, el número 2 con 2 pulgadas, y así sucesivamente. Si alguien sostenía sus manos a 17 pulgadas de distancia para representar el número 17, ¿todos a su alrededor podrían interpretar de inmediato y con precisión esa distancia como 17? Probablemente no. Algunos adivinarían corto (15 o 16) y otros adivinarían largo (18 o 19). ¡Por supuesto, a los pescadores que se jactan de sus capturas no les importa sobreestimaciones en cantidad!

Quizás es por eso que la gente generalmente se ha asentado por símbolos digitales para representar números, especialmente números enteros y enteros, que encuentran la mayor aplicación en la vida cotidiana. Usando los dedos de nuestras manos, tenemos un medio listo para simbolizar enteros de 0 a 10. Podemos hacer marcas de hash en papel, madera o piedra para representar las mismas cantidades con bastante facilidad:

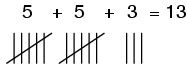
Sin embargo, para números grandes, el sistema de numeración de “marca hash” es demasiado ineficiente.