7.6: Ejemplos de simplificación de circuitos

Comencemos con un circuito de puerta semiconductora que necesita simplificación. Se supone que las señales de entrada “A”, “B” y “C” se proporcionan desde interruptores, sensores o tal vez otros circuitos de puerta. Dónde se originan estas señales no es motivo de preocupación en la tarea de reducción de puertas.

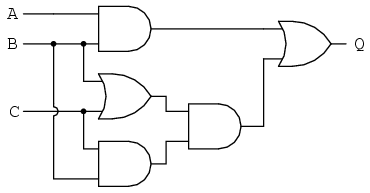
Cómo escribir una expresión booleana para simplificar los circuitos

Nuestro primer paso en la simplificación debe ser escribir una expresión booleana para este circuito. Esta tarea se realiza fácilmente paso a paso si comenzamos escribiendo subexpresiones en la salida de cada puerta, correspondientes a las respectivas señales de entrada para cada puerta. Recuerde que las puertas OR son equivalentes a la suma booleana, mientras que las puertas AND son equivalentes a la multiplicación booleana. Por ejemplo, escribiré subexpresiones en las salidas de las tres primeras puertas:

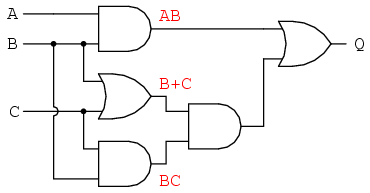
... luego otra subexpresión para la siguiente puerta:

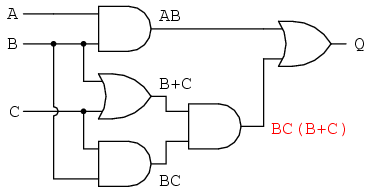
Finalmente, se ve que la salida (“Q”) es igual a la expresión AB + BC (B + C):

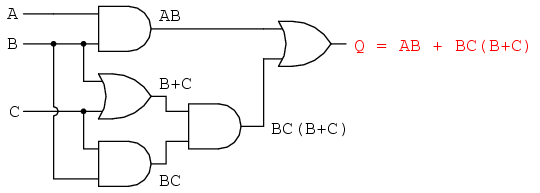
Ahora que tenemos una expresión booleana con la que trabajar, necesitamos aplicar las reglas del álgebra booleana para reducir la expresión a su forma más simple (la más simple se define como requerir la menor cantidad de puertas para implementar):

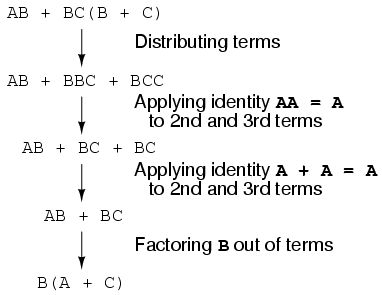
La expresión final, B (A + C), es mucho más simple que la original, pero realiza la misma función. Si desea verificar esto, puede generar una tabla de verdad para ambas expresiones y determinar el estado de Q (la salida de los circuitos) para las ocho combinaciones de estado lógico de A, B y C, para ambos circuitos. Las dos tablas de verdad deben ser idénticas.

Generación de diagramas esquemáticos a partir de expresiones booleanas

Ahora, debemos generar un diagrama esquemático a partir de esta expresión booleana. Para ello, evalúe la expresión, siguiendo el orden matemático adecuado de las operaciones (multiplicación antes de la suma, operaciones dentro de paréntesis antes que cualquier otra cosa), y dibuje puertas para cada paso. Recuerda nuevamente que las puertas OR son equivalentes a la suma booleana, mientras que las puertas AND son equivalentes a la multiplicación booleana. En este caso, comenzaríamos con la subexpresión “A + C”, que es una puerta OR:

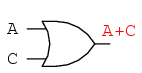
El siguiente paso para evaluar la expresión “B (A + C)” es multiplicar (puerta AND) la señal B por la salida de la puerta anterior (A + C):

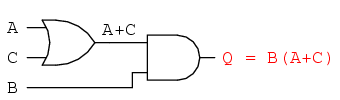
Obviamente, este circuito es mucho más sencillo que el original, teniendo sólo dos puertas lógicas en lugar de cinco. Dicha reducción de componentes da como resultado una mayor velocidad de operación (menos tiempo de retardo desde la transición de la señal de entrada a la transición de la señal de salida), menor consumo de energía, menor costo y mayor confiabilidad

Cómo utilizar la simplificación booleana para circuitos de relés electromecánicos

Los circuitos de relé electromecánicos, que suelen ser más lentos, consumen más energía eléctrica para operar, cuestan más y tienen una vida media más corta que sus homólogos semiconductores, se benefician drásticamente de la simplificación booleana. Consideremos un circuito de ejemplo:

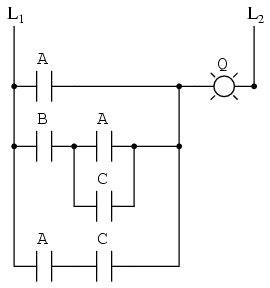
Como antes, nuestro primer paso para reducir este circuito a su forma más simple debe ser desarrollar una expresión booleana a partir del esquema. La forma más fácil que he encontrado para hacer esto es seguir los mismos pasos que normalmente seguiría para reducir una red de resistencias serie-paralelo a una resistencia única y total. Por ejemplo, examine la siguiente red de resistencias con sus resistencias dispuestas en el mismo patrón de conexión que los contactos de relé en el circuito anterior, y la fórmula de resistencia total correspondiente:

Recuerde que los contactos paralelos son equivalentes a la suma booleana, mientras que los contactos de serie son equivalentes a la multiplicación booleana. Escriba una expresión booleana para este circuito de contacto de relé, siguiendo el mismo orden de precedencia que seguiría para reducir una red de resistencias serie-paralelo a una resistencia total. Puede ser útil escribir una subexpresión booleana a la izquierda de cada “peldaño” de escalera, para ayudar a organizar su expresión-escritura:

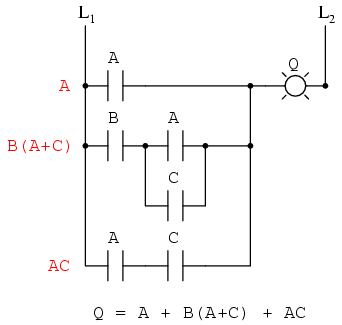
Ahora que tenemos una expresión booleana con la que trabajar, necesitamos aplicar las reglas del álgebra booleana para reducir la expresión a su forma más simple (la más simple se define como requerir la menor cantidad de contactos de relé para implementar):

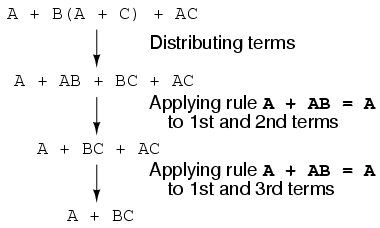
Cuanto más inclinado matemáticamente debería poder ver que los dos pasos que emplean la regla “A + AB = A” pueden combinarse en un solo paso, siendo la regla expandible a: “A + AB + AC + AD +. = A”

Como puede ver, el circuito reducido es mucho más simple que el original, pero realiza la misma función lógica:

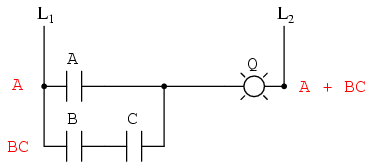
Revisar

• Para convertir un circuito de puerta en una expresión booleana, etiquete cada salida de puerta con una subexpresión booleana correspondiente a las señales de entrada de las puertas, hasta que se alcance una expresión final en la última puerta.
• Para convertir una expresión booleana en un circuito de puerta, evalúe la expresión usando el orden estándar de operaciones: multiplicación antes de la suma y operaciones entre paréntesis antes que cualquier otra cosa.
• Para convertir un circuito lógico de escalera en una expresión booleana, etiquete cada peldaño con una subexpresión booleana correspondiente a las señales de entrada de los contactos, hasta que se alcance una expresión final en la última bobina o luz. Para determinar el orden adecuado de evaluación, trate los contactos como si fueran resistencias, y como si estuvieras determinando la resistencia total de la red serie-paralelo formada por ellos. En otras palabras, primero busque contactos que estén directamente en serie o directamente en paralelo entre sí, luego “contráigalos” en subexpresiones booleanas equivalentes antes de proceder a otros contactos.
• Para convertir una expresión booleana en un circuito lógico de escalera, evalúe la expresión usando el orden estándar de operaciones: multiplicación antes de la suma y operaciones entre paréntesis antes que cualquier otra cosa.