1.1: El Círculo de Unidades

Última actualización
Guardar como PDF

Page ID: 113334

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

¿Cuál es el círculo unitario y por qué es importante en la trigonometría? ¿Cuál es la ecuación para el círculo unitario?
¿Qué se entiende por “envolver la recta numérica alrededor del círculo unitario?” ¿Cómo se usa esto para identificar números reales como la longitud de los arcos en el círculo unitario?
¿Cómo asociamos un arco en el círculo unitario con un intervalo cerrado de números reales?

Actividad inicial

Como se ha indicado, una de las principales razones por las que estudiamos las funciones trigonométricas es poder modelar matemáticamente fenómenos periódicos. Antes de comenzar nuestro estudio matemático de los fenómenos periódicos, aquí hay un pequeño “experimento de pensamiento” a considerar.

Imagina que estás parado en un punto de un círculo y comienzas a caminar alrededor del círculo a una velocidad constante en sentido contrario a las agujas del reloj. También suponga que le toma cuatro minutos caminar completamente alrededor del círculo una vez. Ahora suponga que se encuentra en un punto$P$ de este círculo en un momento determinado$t$.

Describe tu posición en el círculo$2$ minutos después del tiempo$t$.
Describe tu posición en el círculo$4$ minutos después del tiempo$t$.
Describe tu posición en el círculo$6$ minutos después del tiempo$t$.
Describe tu posición en el círculo$8$ minutos después del tiempo$t$.

La idea aquí es que tu posición en el círculo se repita cada$4$ minuto. Después de$2$ minutos, estás en un punto diametralmente opuesto al punto que iniciaste. Después de$4$ minutos, estás de vuelta en tu punto de partida. De hecho, volverás a tu punto de partida después de$8$ minutos,$12$ minutos,$16$ minutos, y así sucesivamente. Esta es la idea del comportamiento periódico.

El círculo unitario y la función de envoltura

Para modelar matemáticamente fenómenos periódicos, necesitaremos funciones que en sí mismas sean periódicas. En otras palabras, buscamos funciones cuyos valores se repitan en patrones regulares y reconocibles. Las funciones familiares como polinomios y funciones exponenciales no presentan un comportamiento periódico, por lo que pasamos a las funciones trigonométricas. Antes de que podamos definir estas funciones, sin embargo, necesitamos una forma de introducir la periodicidad. Lo hacemos de una manera similar al experimento del pensamiento, pero también usamos objetos matemáticos y ecuaciones. La herramienta principal es algo llamado la función de envoltura. En lugar de usar cualquier círculo, usaremos el llamado círculo unitario. Este es el círculo cuyo centro está en el origen y cuyo radio es igual a$1$, y la ecuación para el círculo unitario es$x^{2}+y^{2} = 1$.

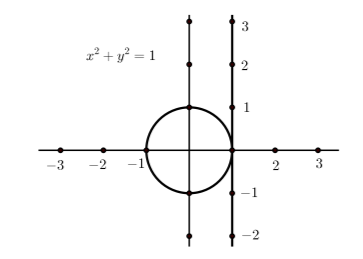
$Figura 1.1.png$

Figura$\PageIndex{1}$: Configuración para envolver la línea numérica alrededor del círculo de la unidad

La figura$\PageIndex{1}$ muestra el círculo unitario con una línea numérica dibujada tangente al círculo en el punto$(1, 0)$. Vamos a “envolver” esta recta numérica alrededor del círculo de la unidad. A diferencia de la recta numérica, la longitud una vez alrededor del círculo unitario es finita. (Recuerde que la fórmula para la circunferencia de un círculo como$2\pi r$ donde$r$ está el radio, por lo que la longitud una vez alrededor del círculo unitario es$2\pi$. Sin embargo, todavía podemos medir distancias y ubicar los puntos en la recta numérica en el círculo unitario envolviendo la recta numérica alrededor del círculo. Envolvemos la parte positiva de esta línea numérica alrededor de la circunferencia del círculo en sentido contrario a las agujas del reloj y envolvemos la parte negativa de la línea numérica alrededor de la circunferencia del círculo unitario en sentido horario.

Dos instantáneas de una animación de este proceso para la envoltura en sentido antihorario se muestran en la Figura$\PageIndex{2}$ y dos de tales instantáneas se muestran en la Figura$\PageIndex{3}$ para la envoltura en sentido horario.

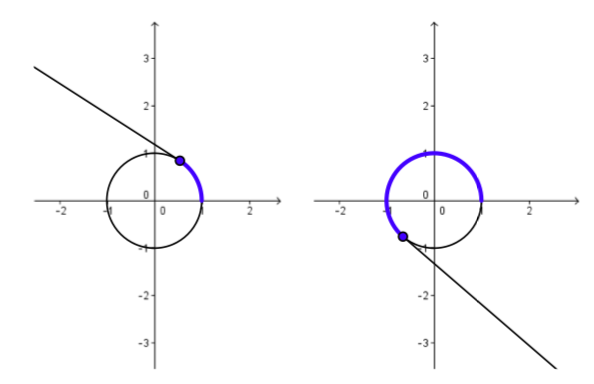
$1.2.png$

Figura$\PageIndex{2}$: Envolviendo la recta numérica positiva alrededor del círculo unitario

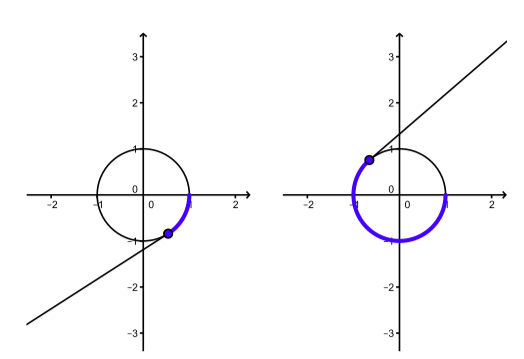
$1.3.png$

Figura$\PageIndex{3}$: Envolviendo la línea numérica negativa alrededor del círculo unitario

A continuación se presenta un enlace a una animación real de este proceso, incluyendo tanto envolturas positivas como envolturas negativas.

http://gvsu.edu/s/Kr

Las figuras$\PageIndex{2}$ y$\PageIndex{3}$ solo muestran una porción de la recta numérica que se envuelve alrededor del círculo. Dado que la recta numérica es infinitamente larga, envolverá el círculo infinitamente muchas veces. Un resultado de esto es que infinitamente muchos números diferentes de la línea numérica se envuelven a la misma ubicación en el círculo unitario.

El número 0 y los números$2\pi$,$-2\pi$, y$4\pi$ (así como otros) se envuelven al punto$(1, 0)$. Por lo general, diremos que estos puntos se mapean al punto$(1, 0)$.
El número$\pi /2$ se mapea al punto$(0, 1)$. Esto se debe a que la circunferencia del círculo unitario es$2\pi$ y así lo es un cuarto de la circunferencia$\frac{1}{4}(2\pi) = \pi/2$.
Si ahora agregamos$2\pi$ a$\pi/2$, vemos que$5\pi/2$ también se mapea a$(0, 1)$. Si restamos$2\pi$ de$\pi/2$, vemos que$-3\pi/2$ también se mapea a eso$(0, 1)$.

Sin embargo, el hecho de que infinitamente muchos números diferentes de la línea numérica se envuelvan a la misma ubicación en el círculo unitario resulta muy útil ya que nos permitirá modelar y representar comportamientos que se repiten o son de naturaleza periódica.

Ejercicio$\PageIndex{1}$

Encuentra dos números diferentes, uno positivo y otro negativo, desde la recta numérica que se envuelve hasta el punto$(-1, 0)$ en el círculo unitario.
Describa todos los números en la línea numérica que se envuelven hasta el punto$(-1, 0)$ en el círculo unitario.
Encuentra dos números diferentes, uno positivo y otro negativo, desde la recta numérica que se envuelve hasta el punto$(0, 1)$ en el círculo unitario.
Encuentra dos números diferentes, uno positivo y otro negativo, desde la recta numérica que se envuelve hasta el punto$(0, -1)$ en el círculo unitario.

Contestar

Algunos números positivos que se envuelven al punto$(-1, 0)$ son$\pi, 3\pi, 5\pi$. Algunos números negativos que se envuelven al punto$(-1, 0)$ son$-\pi, -3\pi, -5\pi$.

Los números a los que se envuelven$(-1, 0)$ son los múltiplos enteros impares de$\pi$.

Algunos números positivos que se envuelven al punto$(0, 1)$ son$\dfrac{\pi}{2}, \dfrac{5\pi}{2}, \dfrac{9\pi}{2}$.

Algunos números negativos que se envuelven al punto$(0, 1)$ son$-\dfrac{\pi}{2}, -\dfrac{5\pi}{2}, -\dfrac{9\pi}{2}$.

Algunos números positivos que se envuelven al punto$(0, -1)$ son$\dfrac{3\pi}{2}, \dfrac{7\pi}{2}, \dfrac{11\pi}{2}$.

Algunos números negativos que se envuelven al punto$(0, -1)$ son$-\dfrac{3\pi}{2}, -\dfrac{5\pi}{2}, -\dfrac{11\pi}{2}$.

Una cosa que deberíamos ver de nuestro trabajo en el ejercicio 1.1 es que los múltiplos enteros de$\pi$ se envuelven ya sea al punto$(1, 0)$ o$(-1, 0)$ y que los múltiplos enteros impares de$\dfrac{\pi}{2}$ se envuelven a ya sea al punto$(0, 1)$ o$(0, -1)$. Dado que la circunferencia del círculo unitario es$2\pi$, no es sorprendente que las partes fraccionarias de$\pi$ y los múltiplos enteros de estas partes fraccionarias de se$\pi$ puedan ubicar en el círculo unitario. Esto se estudiará en el próximo ejercicio.

Ejercicio$\PageIndex{2}$

El siguiente diagrama es un círculo unitario con$24$ puntos igualmente espacian puntos trazados en el círculo. Dado que la circunferencia del círculo es$2\pi$ unidades, el incremento entre dos puntos consecutivos en el círculo es$\dfrac{2\pi}{24} = \dfrac{\pi}{12}$.

Etiquete cada punto con el número real no negativo más pequeño$t$ al que corresponda. Por ejemplo, el punto$(1, 0)$ en el eje x corresponde a$t = 0$. Mudanza

en sentido antihorario a partir de este punto, el segundo punto corresponde a$\dfrac{2\pi}{12} = \dfrac{\pi}{6}$.

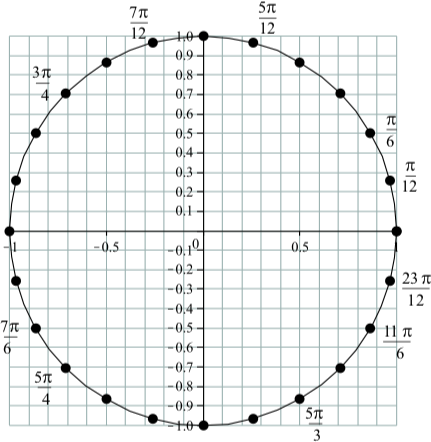
$imageedit_2_6322087183.png$

Figura$\PageIndex{4}$: Puntos en el círculo unitario

Utilizando$\PageIndex{4}$, aproximar la$x$ coordenada -y la$y$ coordenada -de cada una de las siguientes:

El punto en el círculo unitario que corresponde a$t =\dfrac{\pi}{3}$.
El punto en el círculo unitario que corresponde a$t =\dfrac{2\pi}{3}$.
El punto en el círculo unitario que corresponde a$t =\dfrac{4\pi}{3}$.
El punto en el círculo unitario que corresponde a$t =\dfrac{5\pi}{3}$.
El punto en el círculo unitario que corresponde a$t = \dfrac{\pi}{4}$.
El punto en el círculo unitario que corresponde a$t =\dfrac{7\pi}{4}$.

Contestar

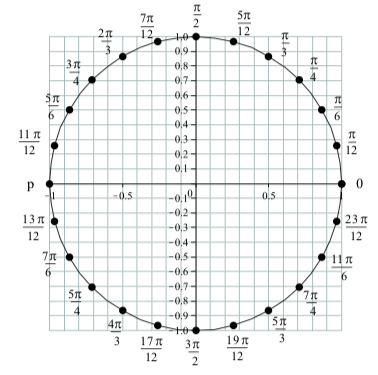
$1.2.png$

Para$t = \dfrac{\pi}{3}$, el punto es aproximadamente$(0.5, 0.87)$. Para$t = \dfrac{2\pi}{3}$, el punto es aproximadamente$(-0.5, 0.87)$. Para$t = \dfrac{4\pi}{3}$, el punto es aproximadamente$(-0.5, -0.87)$. Para$t = \dfrac{5\pi}{3}$, el punto es aproximadamente$(0.5, -0.87)$. Para$t = \dfrac{\pi}{4}$, el punto es aproximadamente$(0.71, 0.71)$. Para$t = \dfrac{7\pi}{4}$, el punto es aproximadamente$(0.71, -0.71)$.

Arcos en el Círculo Unitario

Cuando envolvemos la línea numérica alrededor del círculo unitario, cualquier intervalo cerrado en la línea numérica se mapea a una pieza continua del círculo unitario. Estas piezas se llaman arcos del círculo. Por ejemplo, el segmento$\Big[0, \dfrac{\pi}{2}\Big]$ en la recta numérica se asigna al arco que conecta los puntos$(1, 0)$ y$(0, 1)$ en el círculo unitario como se muestra en$\PageIndex{5}$. En general, cuando$[a, b]$ se mapea un intervalo cerrado a un arco en el círculo unitario, el punto correspondiente a$t = a$ se llama el punto inicial del arco, y el punto correspondiente a$t = a$ se denomina punto terminal del arco. Entonces el arco correspondiente al intervalo cerrado$\Big(0, \dfrac{\pi}{2}\Big)$ tiene punto inicial$(1, 0)$ y punto terminal$(0, 1)$.

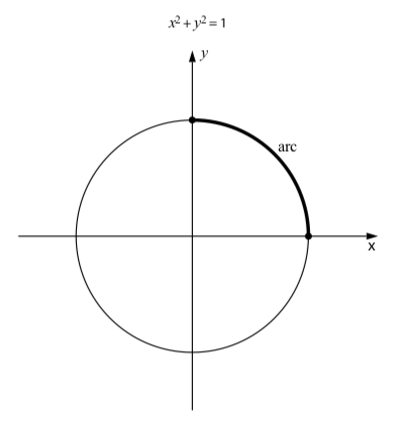
$1.5.png$

Figura$\PageIndex{5}$: Un arco en el círculo unitario

Ejercicio$\PageIndex{3}$

Dibuja los siguientes arcos en el círculo unitario.

El arco que está determinado por el intervalo$[0, \dfrac{\pi}{4}]$ en la recta numérica.
El arco que está determinado por el intervalo$[0, \dfrac{2\pi}{3}]$ en la recta numérica.
El arco que está determinado por el intervalo$[0, -\pi]$ en la recta numérica.

Contestar

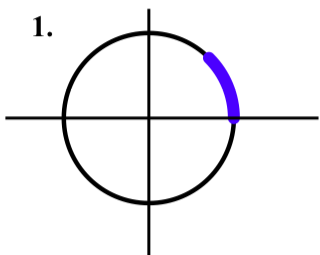
$1.3 1.png$

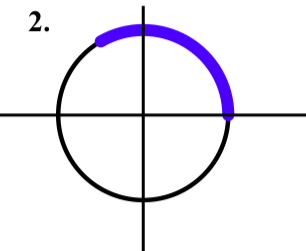
$1.3 2.png$

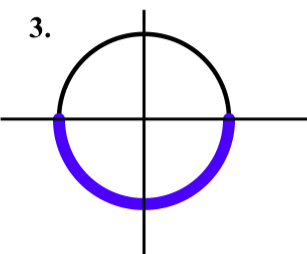
$1.3 3.png$

Coordenadas de Puntos en el Círculo Unitario

Cuando tenemos una ecuación (generalmente en términos de$x$ y$y$) para una curva en el plano y conocemos una de las coordenadas de un punto en esa curva, podemos usar la ecuación para determinar la otra coordenada para el punto en la curva. La ecuación para el círculo unitario es$x^2+y^2 = 1$. Entonces, si conocemos una de las dos coordenadas de un punto en el círculo unitario, podemos sustituir ese valor en la ecuación y resolver los valores de la otra variable.

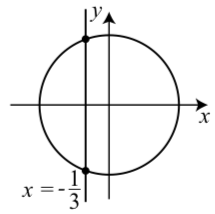
Por ejemplo, supongamos que sabemos que la coordenada x de un punto en el círculo unitario es$-\dfrac{1}{3}$. Esto se ilustra en el siguiente diagrama. Este diagrama muestra el círculo unitario$x^2+y^2 = 1$ y la línea vertical$x = -\dfrac{1}{3}$. Esto demuestra que hay dos puntos en el círculo unitario cuya coordenada x es$-\dfrac{1}{3}$. Podemos encontrar las$y$ coordenadas sustituyendo el$x$ -valor en la ecuación y resolviendo para$y$.

$example.png$

\[\begin{align*} x^2+y^2 &= 1 \\[4pt] (-\dfrac{1}{3})^2+y^2 &= 1 \\[4pt] \dfrac{1}{9}+y^2 &= 1 \\[4pt] y^2 &= \dfrac{8}{9} \end{align*}\]

Ya que$y^2 = \dfrac{8}{9}$, vemos eso$y = \pm\sqrt{\dfrac{8}{9}}$ y así$y = \pm\dfrac{\sqrt{8}}{3}$. Entonces los dos puntos en el círculo unitario cuya$x$ coordenada es$-\dfrac{1}{3}$ son

\[ \left(-\dfrac{1}{3}, \dfrac{\sqrt{8}}{3}\right),\]

que está en el segundo cuadrante y

\[ \left(-\dfrac{1}{3}, -\dfrac{\sqrt{8}}{3}\right),\]

que se encuentra en el tercer cuadrante.

El primer punto está en el segundo cuadrante y el segundo punto está en el tercer cuadrante. Ahora podemos usar una calculadora para verificar eso$\dfrac{\sqrt{8}}{3} \approx 0.9428$. Esto parece consistente con el diagrama que usamos para este problema.

Ejercicio$\PageIndex{4}$

Encuentra todos los puntos del círculo unitario cuya$y$ coordenada es$\dfrac{1}{2}$.
Encuentra todos los puntos del círculo unitario cuya coordenada x es$\dfrac{\sqrt{5}}{4}$.

Contestar

Nosotros sustituimos$y = \dfrac{1}{2}$ en$x^{2} + y^{2} = 1$.

\[x^{2} + (\dfrac{1}{2})^{2} = 1\]
\[x^{2} = \dfrac{3}{4}\]
\[x = \pm\dfrac{\sqrt{3}}{2}\]

Los dos puntos son$(\dfrac{\sqrt{3}}{2}, \dfrac{1}{2})$ y$(-\dfrac{\sqrt{3}}{2}, \dfrac{1}{2})$

Nosotros sustituimos$y = \dfrac{\sqrt{5}}{4}$ en$x^{2} + y^{2} = 1$.

\[(\dfrac{\sqrt{5}}{4})^{2} + y^{2} = 1\]
\[y^{2} = \dfrac{11}{16}\]
\[x = \pm\dfrac{\sqrt{11}}{4}\]

Los dos puntos son$(\dfrac{\sqrt{5}}{4}, \dfrac{\sqrt{11}}{4})$ y$(\dfrac{\sqrt{5}}{4}, -\dfrac{\sqrt{11}}{4})$.

Resumen

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

El círculo unitario es el círculo de radio 1 que está centrado en el origen. La ecuación del círculo unitario es$x^2+y^2 = 1$. Es importante porque vamos a utilizar esto como herramienta para modelar fenómenos periódicos.
“Envolvemos” la recta numérica alrededor del círculo unitario dibujando una línea numérica que es tangente al círculo unitario en el punto$(1, 0)$. Envolvemos la parte positiva de la línea numérica alrededor del círculo unitario en sentido contrario a las agujas del reloj y envolvemos la parte negativa de la línea numérica alrededor del círculo unitario en el sentido de las agujas del reloj.
Cuando envolvemos la línea numérica alrededor del círculo unitario, cualquier intervalo cerrado de números reales se mapea a una pieza continua del círculo unitario, que se llama arco del círculo. Cuando el intervalo cerrado$(a, b)$ se mapea a un arco en el círculo unitario, el punto correspondiente a$t = a$ se llama el punto inicial del arco, y el punto correspondiente a$t = a$ se denomina punto terminal del arco.