1.2: Las funciones coseno y seno

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• Si el número real\(t\) representa la longitud (firmada) de un arco, ¿cómo definimos\(\cos(t)\) y\(\sin(t)\)?
• ¿En qué cuadrantes (del punto terminal de un arco t en el círculo unitario) es\(\cos(t)\) positivo (negativo)? ¿En qué cuadrantes (del punto terminal de un arco\(t\) en el círculo unitario) es\(\sin(t)\) positivo (negativo)?
• ¿Qué es la identidad pitagórica? ¿Cómo se deriva esta identidad de la ecuación para el círculo unitario?

Actividad inicial

1. ¿Qué es el círculo unitario? ¿Cuál es la ecuación del círculo unitario?
2. Revisar el Ejercicio 1.4 en la página 9.
3. Revisar la versión completada de Figura1.4 que se encuentra en las respuestas para Ejercicio 1.2 en la página 6.
   1. ¿Cuál es el punto terminal del arco en el círculo unitario que corresponde al intervalo\([0, \dfrac{\pi}{2}]\)?
   2. ¿Cuál es el punto terminal del arco en el círculo unitario que corresponde al intervalo\([0, \pi]\)?
   3. ¿Cuál es el punto terminal del arco en el círculo unitario que corresponde al intervalo\([0, \dfrac{3\pi}{2}]\)?
   4. ¿Cuál es el punto terminal del arco en el círculo unitario que corresponde al intervalo\([0, -\dfrac{\pi}{2}]\)?

Las funciones coseno y seno

Comenzamos nuestro estudio de la trigonometría aprendiendo sobre el círculo unitario, cómo envolver la línea numérica alrededor del círculo unitario y cómo construir arcos en el círculo unitario. Ahora podemos usar estas ideas para definir las dos principales funciones circulares o trigonométricas. Estas funciones circulares nos permitirán modelar fenómenos periódicos como las mareas, la cantidad de luz solar durante los días del año, órbitas de planetas, y muchos otros.

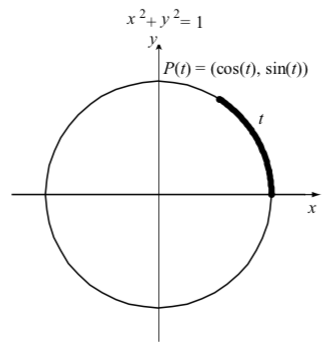
Figura\(\PageIndex{1}\): Las funciones circulares

Puede parecer que el círculo unitario es un objeto bastante simple y de poco interés, pero los matemáticos casi siempre pueden encontrar algo fascinante incluso en objetos tan simples. Por ejemplo, definimos las dos funciones circulares principales, el coseno y el seno en términos del círculo unitario de la siguiente manera. La figura\(\PageIndex{1}\) muestra un arco de longitud\(t\) en el círculo unitario. Este arco comienza en el punto\((1, 0)\) y termina en su punto terminal\(P(t)\). Luego definimos el coseno y el seno del arco\(t\) como las\(y\) coordenadas\(x\) y del punto\(P\), de modo que\(P(t) = (\cos(t), sin(t))\) (abreviamos el coseno como\(\cos\) y el seno como\(\sin\)). Entonces los valores coseno y seno están determinados por el arco\(t\) y el coseno y el seno son funciones del arco\(t\). Dado que el arco se encuentra en el círculo unitario, llamamos a las funciones circulares coseno y seno. Una parte importante de la trigonometría es el estudio del coseno y seno y los fenómenos periódicos que estas funciones pueden modelar. Esta es una razón por la que las funciones circulares también se denominan funciones trigonométricas.

Nota

Según el sitio web Los primeros usos conocidos de algunas de las palabras de las matemáticas en jeff560.tripod.com/mathword.html, el origen de la palabra seno es el sánscrito a través del árabe y el latín. Si bien los relatos del origen real difieren, parece que la obra sánscrita “jya” (acorde) fue tomada al árabe como “jiba”, pero luego fue traducida al latín como “jaib” (bahía) que se convirtió en “seno” (bahía o curva). Esta palabra fue entonces anglicizada para convertirse en nuestro “seno”. La palabra coseno comenzó con Platón de Tívoli que utilizan la expresión “chorda residui”. Si bien la palabra latina chorda era una mejor traducción de la palabra sánscrito-árabe para seno que la palabra seno, esa palabra ya estaba en uso. Así, “chorda residui” se convirtió en “coseno”.

Nota

En matemáticas, siempre creamos definiciones formales para los objetos que comúnmente usamos. Las definiciones son de importancia crítica porque con definiciones acordadas, todos tendrán un entendimiento común de lo que significan los términos. Sin- un entendimiento tan común, habría mucha confusión ya que diferentes personas tienen diferentes significados para diversos términos. Por lo tanto, son necesarias definiciones cuidadosas y precisas para desarrollar las propiedades matemáticas de estos objetos. Para aprender y comprender la trigonometría, una persona necesita poder explicar cómo se definen las funciones circulares. Entonces ahora es un buen momento para comenzar a trabajar en la comprensión de estas definiciones.

Definiciones: coseno y seno

Si el número real t es la longitud dirigida de un arco (positivo o negativo) medido en el círculo unitario\(x^2 + y^2 = 1\) (con sentido contrario a las agujas del reloj como la dirección positiva) con punto inicial\((1, 0)\) y punto terminal\((x, y)\), entonces el coseno de\(t\), denotado\(\cos(t)\), y seno de t, denotado\(\sin(t)\), se definen como\[\cos (t) = x\] y\[\sin (t) = y.\]

La Figura 1.6 ilustra estas definiciones para un arco cuyo punto terminal se encuentra en el primer cuadrante.

En este momento, no es posible determinar los valores exactos de las funciones coseno y seno para valores específicos de\(t\). Se puede hacer, sin embargo, si el punto terminal de un arco de longitud\(t\) se encuentra en el\(x\) eje -eje o el\(y\) eje -eje. Por ejemplo, dado que la circunferencia del círculo unitario es\(2\pi\), un arco de longitud lo\(t = \pi\) tendrá punto terminal a mitad de camino alrededor del círculo desde el punto\((1, 0)\). Es decir, el punto terminal está en\((1, 0)\). Por lo tanto,\[\cos (\pi) = -1\] y\[\sin (\pi) = 0.\]

Ejercicio\(\PageIndex{1}\)

Determinar los valores exactos de cada uno de los siguientes:

1. \(\cos(\dfrac{\pi}{2})\)y\(\sin(\dfrac{\pi}{2})\).
2. \(\cos(\dfrac{3\pi}{2})\)y\(\sin(\dfrac{3\pi}{2})\).
3. \(\cos(0)\)y\(sin(0)\).
4. \(\cos(-\dfrac{\pi}{2})\)y\(\sin(-\dfrac{\pi}{2})\).
5. \(\cos(2\pi)\)y\(\sin(2\pi)\).
6. \(cos(-\pi)\)y\(\sin(-\pi)\).

Nota Importante: Dado que el coseno y el seno son funciones de un arco cuya longitud es el número real t, la entrada t determina la salida del coseno y sin. Como resultado, es necesario especificar el valor de entrada cuando se trabaja con el coseno y el seno. En otras palabras, SIEMPRE escribimos\(\cos(t)\) dónde\(t\) está la entrada del número real, y NUNCA solo\(\cos\). Para reiterar, el coseno y el seno son funciones, por lo que DEBEMOS indicar la entrada a estas funciones.

Contestar

1. \[\cos(\dfrac{\pi}{2}) = 0\]\[\sin(\dfrac{\pi}{2}) = 1\]
2. \[\cos(\dfrac{3\pi}{2}) = 0\]\[\sin(\dfrac{3\pi}{2}) = -1\]
3. \[\cos(0) = 1\]\[\sin(0) = 1\]
4. \[\cos(-\dfrac{\pi}{2}) = 0\]\[\sin(-\dfrac{\pi}{2}) = -1\]
5. \[\cos(2\pi) = 0\]\[\sin(2\pi) = 1\]
6. \[\cos(-\pi) = -1\]\[\sin(-\pi) = 0\]

Ejercicio\(\PageIndex{2}\)

Para este Ejercicio, utilizaremos el Applet de Geogebra llamado Puntos Terminales de Arcos en el Círculo de Unidades. Una dirección web para este applet es

http://gvsu.edu/s/JY

Para este applet, controlamos el valor de la entrada\(t\) con el deslizador para\(t\). Los valores de\(t\) rango de\(-20\) a\(20\) en incrementos de\(0.5\). Para un valor dado de\(t\), se dibuja un arco de longitud\(t\) y se muestran las coordenadas del punto terminal de ese arco. Utilice este applet para encontrar valores aproximados para cada uno de los siguientes:

1. \(\cos(1)\)y\(\sin(1)\)
2. \(\cos(2)\)y\(\sin(2)\)
3. \(\cos(-4)\)y\(\sin(-4)\)
4. \(\cos(5.5)\)y\(\sin(5.5)\)
5. \(\cos(15)\)y\(\sin(15)\)
6. \(\cos(-15)\)y\(\sin(-15)\)

Contestar

1. \[\cos(1) \approx 0.5403, \sin(1) \approx 0.8415\]
2. \[\cos(2) \approx -0.4161, \sin(2) \approx 0.9093\]
3. \[\cos(-4) \approx -0.6536, \sin(-4) \approx 0.7568\]
4. \[\cos(5.5) \approx 0.7807, \sin(5.5) \approx -0.7055\]
5. \[\cos(15) \approx -0.7597, \sin(15) \approx 0.6503\]
6. \[\cos(-15) \approx -0.7597, \sin(-15) \approx 0.6503\]

Algunas propiedades de las funciones coseno y seno

Las funciones coseno y seno se denominan funciones circulares porque sus valores están determinados por las coordenadas de puntos en el círculo unitario. Para cada número real\(t\), hay un arco correspondiente que comienza en el punto\((1, 0)\) de longitud (dirigida)\(t\) que se encuentra en el círculo unitario. Las coordenadas del punto final de este arco determinan los valores de\(\cos(t\) y\(\sin(t\).

En cursos previos de matemáticas, hemos aprendido que el dominio de una función es el conjunto de todas las entradas que dan una salida definida. También hemos aprendido que el rango de una función es el conjunto de todas las salidas posibles de la función.

Ejercicio\(\PageIndex{3}\)

1. ¿Cuál es el dominio de la función coseno? ¿Por qué?
2. ¿Cuál es el dominio de la función sinusoidal? ¿Por qué?
3. ¿Cuál es la\(x\) coordenada más grande que puede tener un punto en el círculo unitario? ¿Cuál es la\(x\) coordenada más pequeña que puede tener un punto en el círculo unitario? ¿Qué nos dice esto sobre el rango de la función coseno? ¿Por qué?
4. ¿Cuál es la\(y\) coordenada más grande que puede tener un punto en el círculo unitario? ¿Cuál es la\(y\) coordenada más pequeña que puede tener un punto en el círculo unitario? ¿Qué nos dice esto sobre el rango de la función sinusoidal? ¿Por qué?

Contestar

1. Como podemos envolver cualquier número en el círculo unitario, siempre podemos encontrar el punto terminal de un arco que corresponda a cualquier número. Entonces se define el coseno de cualquier número real y el dominio de la función coseno es el conjunto de todos los números reales.
2. Por la misma razón que para la función coseno, el dominio de la función sinusoidal es el conjunto de todos los números reales.
3. En el círculo unitario, la coordenada x más grande que puede tener un punto es 1 y la coordenada x más pequeña que puede tener un punto es 1. Dado que la salida de la función coseno es la coordenada x de un punto en el círculo unitario, el rango de la función coseno es el intervalo cerrado\([-1, 1]\). Eso significa\(-1 \leq \cos(t) \leq 1\) para cualquier número real\(t\).
4. En el círculo unitario, la coordenada y más grande que puede tener un punto es 1 y la coordenada y más pequeña que puede tener un punto es 1. Dado que la salida de la función sinusoidal es la coordenada y de un punto en el círculo unitario, el rango de la función sinusoidal es el intervalo cerrado\([-1, 1]\). Eso significa\(-1 \leq \sin(t) \leq 1\) para cualquier número real\(t\).

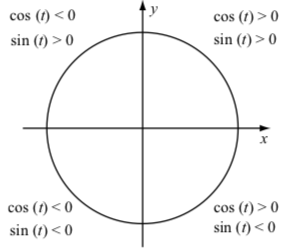
Aunque es posible que no podamos calcular los valores exactos para muchas entradas para las funciones coseno y seno, podemos usar nuestro conocimiento del sistema de coordenadas y sus cuadrantes para determinar si ciertos valores de coseno y seno son positivos o negativos. La idea es que los signos de las coordenadas de un punto\(P(x, y)\) que se traza en el plano de coordenadas están determinados por el cuadrante en el que se encuentra el punto (a menos que se encuentre sobre uno de los ejes). La figura\(\PageIndex{2}\) resume estos resultados para los signos de los valores de la función coseno y seno. La columna izquierda en la tabla es para la ubicación del punto terminal de un arco determinado por el número real\(t\).

Figura\(\PageIndex{2}\): Signos de las funciones coseno y seno

Cuadrante	\(\cos(t)\)	\(\sin(t)\)
QI	\ (\ cos (t)\) ">positivo	\ (\ sin (t)\) ">positivo
QII	\ (\ cos (t)\) ">negativo	\ (\ sin (t)\) ">positivo
QIII	\ (\ cos (t)\) ">negativo	\ (\ sin (t)\) ">negativo
QIV	\ (\ cos (t)\) ">positivo	\ (\ sin (t)\) ">negativo

Lo que tenemos que hacer ahora es determinar en qué cuadrante se encuentra el punto terminal de un arco determinado por un número real t. Podemos hacer esto usando una vez más el hecho de que la circunferencia del círculo unitario es\(2\pi\), y cuando nos movemos alrededor del círculo unitario desde el punto .1; 0/ en la dirección positiva (en sentido contrario a las agujas del reloj), cruzaremos uno de los ejes de coordenadas cada cuarto de revolución. Por ejemplo, si\(0 < t < \dfrac{\pi}{2}\), el punto terminal del arco determinado por\(t\) está en el primer cuadrante y\(\cos(t) > 0\) y\(\sin(t) > 0\).

Ejercicio\(\PageIndex{4}\)

1. Si\( \dfrac{\pi}{2} < t < \pi\), entonces ¿cuáles son los signos de\(\cos(t)\) y\(\sin(t)\)?
2. Si\( \pi < t < \dfrac{3\pi}{2}\), entonces ¿cuáles son los signos de\(\cos(t)\) y\(\sin(t)\)?
3. Si\( \dfrac{3\pi}{2} < t < 2\pi\), entonces ¿cuáles son los signos de\(\cos(t)\) y\(\sin(t)\)?
4. Si\( \dfrac{5\pi}{2} < t < 3\pi\), entonces ¿cuáles son los signos de\(\cos(t)\) y\(\sin(t)\)?
5. ¿Para qué valores de\(t\) (entre\(0\) y\(2\pi\)) es\(\cos(t)\) positivo? ¿Por qué?
6. ¿Para qué valores de\(t\) (entre\(0\) y\(2\pi\)) es\(\sin(t)\) positivo? ¿Por qué?
7. ¿Para qué valores de\(t\) (entre\(0\) y\(2\pi\)) es\(\cos(t)\) negativo? ¿Por qué?
8. ¿Para qué valores de\(t\) (entre\(0\) y\(2\pi\)) es\(\sin(t)\) negativo? ¿Por qué?

Contestar

1. Si\(\dfrac{\pi}{2} < t < \pi\), entonces el punto terminal del arco\(t\) está en el segundo cuadrante y así\(\cos(t) < 0\) y\(\sin(t) > 0\).
2. Si\(\pi < t < \dfrac{3\pi}{2}\), entonces el punto terminal del arco t está en el tercer cuadrante y así\(\cos(t) < 0\) y\(\sin(t) < 0\).
3. Si\(\dfrac{3\pi}{2} < t < 2\pi\), entonces el punto terminal del arco t está en el cuarto cuadrante y así\(\cos(t) > 0\) y\(\sin(t) < 0\).
4. Si\(\dfrac{5\pi}{2} < t < 3\pi\), entonces el punto terminal del arco t está en el segundo cuadrante y así\(\cos(t) > 0\) y\(\sin(t) > 0\).
5. Tenga en cuenta que\(\cos(t) = 0\) en\(t = \dfrac{\pi}{2}\) y\(t = \dfrac{3\pi}{2}\). Dado que\(\cos(t)\) es la coordenada x del punto terminal del arco\(t\), la respuesta anterior muestra que\(\cos(t)\) es positiva cuando\(t\) está en uno de los intervalos\([0, \dfrac{\pi}{2})\) o\((\dfrac{3\pi}{2}, 2\pi]\).
6. Tenga en cuenta que\(\sin(t) = 0\) en\(t = 0\) y\(t = \pi\). Dado que\(\sin(t)\) es la coordenada x del punto terminal del arco\(t\), la respuesta anterior muestra que\(\sin(t)\) es positiva cuando\(t\) está en uno de los intervalos\((0, \pi)\).
7. Tenga en cuenta que\(\cos(t) = 0\) en\(t = \dfrac{\pi}{2}\) y\(t = \dfrac{3\pi}{2}\). Dado que\(\cos(t)\) es la coordenada x del punto terminal del arco\(t\), la respuesta anterior muestra que\(\cos(t)\) es positiva cuando\(t\) está en el intervalo\((\dfrac{\pi}{2}, \dfrac{3\pi}{2})\).
8. Tenga en cuenta que\(\sin(t) = 0\) en\(t = \pi\) y\(t = 2\pi\). Dado que\(\sin(t)\) es la coordenada x del punto terminal del arco\(t\), la respuesta anterior muestra que\(\sin(t)\) es positiva cuando\(t\) está en uno de los intervalos\([0, \dfrac{\pi}{2})\) o\((\pi, 2\pi)\).

Ejercicio\(\PageIndex{5}\)

Utilice los resultados resumidos en la Figura\(\PageIndex{2}\) para ayudar a determinar si las siguientes cantidades son positivas, negativas o cero. (No utilice una calculadora.)

1. \(\cos(\dfrac{\pi}{5})\)
2. \(\sin(\dfrac{\pi}{5})\)
3. \(\cos(\dfrac{5\pi}{8})\)
4. \(\sin(\dfrac{5\pi}{8})\)
5. \(\cos(\dfrac{-9\pi}{16})\)
6. \(\sin(\dfrac{-9\pi}{16})\)
7. \(\cos(\dfrac{-25\pi}{12})\)
8. \(\sin(\dfrac{-25\pi}{12})\)

Contestar

1. Ya que\(0 < \dfrac{\pi}{5} < \dfrac{\pi}{2}\), el punto terminal del arco\(\dfrac{\pi}{5}\) se encuentra en el primer cuadrante. Por lo tanto,\(\cos(\dfrac{\pi}{5})\) es positivo.
2. El uso de la información acerca de\(t\) en (1),\(\sin(\dfrac{\pi}{5})\) es positivo.
3. Podemos escribir\(\dfrac{\pi}{2}\) como\(\dfrac{4\pi}{8}\) y\(\pi\) como\(\dfrac{8\pi}{8}\), así\(\dfrac{\pi}{2}\ < \dfrac{5\pi}{8} < \pi\). Esto pone el punto terminal del arco\(\dfrac{5\pi}{8}\) en el segundo cuadrante. Por lo tanto,\(\cos(\dfrac{5\pi}{8})\) es negativo.
4. El uso de la información acerca de\(t\) en (3),\(\sin(\dfrac{5\pi}{8})\) es negativo.
5. Podemos escribir\(-\dfrac{\pi}{2}\) como\(\dfrac{-8\pi}{16}\) y\(-\pi\) como\(\dfrac{-16\pi}{16}\), así\(-\pi < \dfrac{-9\pi}{16} < -\dfrac{\pi}{2}\). Esto pone el punto terminal del arco\(\dfrac{-9\pi}{16}\) en el tercer cuadrante. Por lo tanto, (\ cos (\ dfrac {-9\ pi} {16})\) es negativo.
6. Usando la información acerca de\(t\) in (5), (\ sin (\ dfrac {-9\ pi} {16})\) es negativo.
7. Podemos escribir\(-2\pi\) como\(\dfrac{-24\pi}{12}\) y\(-\dfrac{5\pi}{2}\) como\(\dfrac{-30\pi}{12}\), así\(\dfrac{-5\pi}{2} < \dfrac{-25\pi}{12} < 2\pi\). Esto pone el punto terminal del arco\(\cos(\dfrac{-25\pi}{12})\) en el cuarto cuadrante.
8. Usar la información sobre el arco\(t\) en (7),\(\sin(\dfrac{-25\pi}{12})\) es negativo.

La identidad pitagórica

En matemáticas, una identidad es una afirmación que es verdadera para todos los valores de las variables para las que se define. En cursos anteriores, hemos trabajado con identidades algebraicas como

\[7x+12x = 19x\]\[a^2 - b^2 = (a + b)(a - b)\]

\[a + b = b + a\]

\[x(y + z) = xy + xz\]

donde se entiende que todas las variables representan números reales. En trigonometría, desarrollaremos muchas de las llamadas identidades trigonométricas. El siguiente Ejercicio introduce una identidad de este tipo entre las funciones coseno y seno.

Ejercicio\(\PageIndex{6}\)

Sabemos que la ecuación para el círculo unitario es\(x^2 + y^2 = 1\). También sabemos que si\(t\) es un número real, entonces el punto terminal del arco determinado por\(t\) es el punto\((\cos(t), \sin(t))\) y que este punto se encuentra en el círculo unitario. Utilice esta información para desarrollar una identidad que involucre\(\cos(t)\) y\(\sin(t)\).

Contestar

Cualquier punto del círculo unitario satisface la ecuación\(x^{2} + y^{2} = 1\). Dado que\((\cos(t), \sin(t))\) es un punto en el círculo unitario, se deduce que\((\cos(t))^{2} + (\sin(t))^{2} = 1\) o\[\cos^{2}(t) + \sin^{2}(t) = 1.\]

Definición: Identidad pitagórica

Usando las definiciones\(x = \cos(t)\) y\(y = \sin(t)\) junto con la ecuación para el círculo unitario, obtenemos la siguiente identidad, que es quizás la identidad trigonométrica más importante.

Por cada número real\(t\),

\[(\cos(t))^2 + (\sin(t))^2 = 1.\]

A esto se le llama la Identidad Pitagórica. A menudo usamos la notación abreviada\(\cos^2(t)\) para\((\cos(t))^2\) y\(\sin^2(t)\) para\((\sin(t))^2\) y escribimos

\[\cos^2(t) + \sin^2(t) = 1.\]

Nota Importante sobre Notación:

Siempre recuerda eso por\(\cos^2(t)\) lo que queremos decir\((\cos(t))^2\). Además, tenga en cuenta que\(\cos^2(t)\) es diferente de\(\cos(t^2)\).

La Identidad Pitagórica nos permite determinar el valor de\(\cos(t)\) o\(\sin(t)\) si conocemos el valor del otro y del cuadrante en el que se\(t\) encuentra el punto terminal del arco. Esto se ilustra en el siguiente ejemplo.

Ejemplo\(\PageIndex{1}\)

Supongamos que\(\cos(t) = \dfrac{2}{5}\) y el punto terminal de arco\((t)\) se encuentra en el cuarto cuadrante.5 Utilice esta información para determinar el valor de\(\sin(t)\).

Solución

La herramienta principal que usaremos es la Identidad Pitagórica, pero tenga en cuenta que el punto terminal para el arco\(t\) es el punto\((\cos(t), \sin(t))\). Es decir,\(x = \cos(t)\) y\(y = \sin(t)\) Entonces este problema es muy similar a usar la ecuación\(x^2 + y^2 = 1\) para el círculo unitario y sustituir\(x = \dfrac{2}{5}\).

Usando la Identidad Pitagórica, vemos entonces que

\[\cos^2(t) + \sin^2(t) = 1\]

\[ (\dfrac{2}{5})^2+ \sin^2(t) = 1\]

\[\dfrac{4}{25} + \sin^2(t) = 1\]

\[ \sin^2(t) = 1 - \dfrac{4}{25} \]

\[ \sin^2(t) = \dfrac{21}{25} \]

Esto quiere decir que\(\sin(t) = \pm\sqrt{\dfrac{21}{25}}\), y como el punto terminal del arco\((t)\) está en el cuarto cuadrante, eso lo sabemos\(\sin(t) < 0\). Por lo tanto,\(\sin(t) = -\sqrt{\dfrac{21}{25}}\). Ya que\(\sqrt{25} = 5\), podemos escribir

\[\sin(t) = -\sqrt{\dfrac{21}{25}} = -\dfrac{\sqrt{21}}{5}.\]

Ejercicio\(\PageIndex{7}\)

1. Si\(\cos(t) = \dfrac{1}{2}\) y el punto terminal del arco\(t\) está en el cuarto cuadrante, determine el valor de\(\sin(t)\).
2. Si\(\sin(t) = -\dfrac{2}{3}\) y\(\pi < t < \dfrac{3\pi}{2}\), determinar el valor de\(\cos(t)\).

Contestar

1. Ya que\(\cos(t) = \dfrac{1}{2}\), podemos utilizar la Identidad Pitagórica para obtener

\ [(\ dfrac {1} {2}) ^ {2} +\ sin^ {2} (t) = 1]

\[\dfrac{1}{4} + \sin^{2}(t) = 1\]

\[\sin^{2}(t) = \dfrac{3}{4}\]

\[\sin(t) = \pm\dfrac{\sqrt{3}}{4}\]

Observe que no podemos determinar el signo de\(\sin(t)\) usar solo la Identidad Pitagórica. Necesitamos más información sobre el arco\(t\). En este caso, se nos da que el punto terminal del arco\(t\) está en el cuarto cuadrante, y por lo tanto,,\(\sin(t) < 0\). En consecuencia,

\[\sin(t) = -\sqrt{\dfrac{3}{4}} = -\dfrac{\sqrt{3}}{2}\]

2. Ya que\(\sin(t) = -\dfrac{2}{3}\), podemos utilizar la Identidad Pitagórica para obtener

\ [\ cos^ {2} (t) + (-\ dfrac {2} {3}) ^ {2} = 1]

\[\cos^{2}(t) + \dfrac{4}{9} = 1\]

\[\cos^{2}(t) = \dfrac{5}{9}\]

\[\sin(t) = \pm\dfrac{\sqrt{5}}{9}\]

Una vez más, necesitamos información sobre el arco\(t\) para determinar el signo de\(\cos(t)\). En este caso, se nos da eso\(\pi < t < \dfrac{3\pi}{2}\). De ahí que el punto terminal del arco t se encuentre en el tercer cuadrante y así,\(\sin(t) < 0\). Por lo tanto,

\[\cos(t) = -\sqrt{\dfrac{5}{9}} = \dfrac{\sqrt{5}}{3}.\]

Resumen

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

• Si el número real t es la longitud dirigida de un arco (positivo o negativo) medido en el círculo unitario\(x^2 + y^2 = 1\) (con sentido contrario a las agujas del reloj como la dirección positiva) con punto inicial\((1, 0)\) y punto terminal\((x, y)\), entonces\(\cos(t) = x\) y\(\sin(t) = y\).

• Los signos de\(\cos(t)\) y\(\sin(t)\) están determinados por el cuadrante en el que se\(t\) encuentra el punto terminal de un arco.

Cuadrante	\(\cos(t)\)	\(\sin(t)\)
QI	\ (\ cos (t)\) ">positivo	\ (\ sin (t)\) ">positivo
QII	\ (\ cos (t)\) ">negativo	\ (\ sin (t)\) ">positivo
QIII	\ (\ cos (t)\) ">negativo	\ (\ sin (t)\) ">negativo
QIV	\ (\ cos (t)\) ">positivo	\ (\ sin (t)\) ">negativo

• Una de las identidades más importantes en trigonometría, llamada Identidad Pitagórica, se deriva de la ecuación para el círculo unitario y establece:

Por cada número real\(t\),\[\cos^2(t) + \sin^2(t) = 1.\nonumber\]