1.4: Velocidad y Velocidad Angular

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Qué es la longitud del arco?
• ¿Cuál es la diferencia entre linear velocity y angular velocity?
• ¿Cuáles son las fórmulas que relacionan la velocidad lineal con la velocidad angular?

Actividad inicial

1. ¿Cuál es la fórmula para la circunferencia\(C\) de un círculo cuyo radio es\(r\)?
2. Supongamos que la persona\(A\) camina a lo largo de la circunferencia de un círculo con un radio de 10 pies, y la persona B camina a lo largo de la circunferencia de un círculo de radio de 20 pies. También, supongamos que se necesitan ambos\(A\) y\(B\) 1 minuto para caminar una cuarta parte de la circunferencia de sus respectivos círculos (una cuarta parte de una revolución completa). ¿Quién caminó más lejos?
3. Supongamos que ambas personas siguen caminando al mismo ritmo que hicieron durante el primer minuto. ¿Cuántas revoluciones completas del círculo caminará cada persona en 8 minutos? ¿En 10 minutos?

Longitud del arco en un círculo

En la Sección 1.3, aprendimos que la medida radianes de un ángulo era igual a la longitud del arco en el círculo unitario asociado a ese ángulo. Entonces un arco de longitud 1 en el círculo unitario subtiende un ángulo de 1 radián. Habrá momentos en los que también será útil conocer la longitud de los arcos en otros círculos que subtiendan el mismo ángulo.

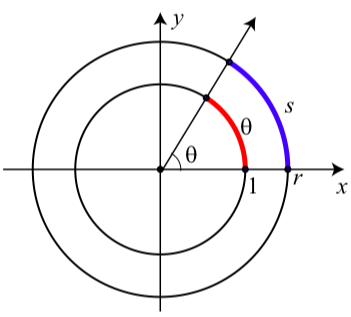
Figura\(\PageIndex{1}\): Arcos subtendidos por un ángulo de 1 radián.

En la Figura\(\PageIndex{1}\), el círculo interno tiene un radio de 1, el círculo exterior tiene un radio de\(r\), y el ángulo mostrado tiene una medida de\(\theta\) radianes. Entonces la longitud del arco en el círculo unitario subtendido por el ángulo es\(\theta\), y hemos utilizado s para representar la longitud del arco en el círculo de radio\(r\) subtendido por el ángulo.

Recordemos que la circunferencia de un círculo de radio\(r\) es\(2\pi r\) mientras que la circunferencia del círculo de radio 1 es\(2\pi\). Por lo tanto, la relación de una longitud de arco\(s\) en el círculo de radio\(r\) que subtiende un ángulo de\(\theta\) radianes con respecto al arco correspondiente en el círculo unitario es\(\dfrac{2\pi r}{2\pi} = r\). Por lo que se deduce que

\[\dfrac{s}{\theta} = \dfrac{2\pi r}{\pi}\]

\[s = r\theta\]

Definición

En un círculo de radio\(r\), la longitud del arco s interceptada por un ángulo central con medida de radianes es

\[s = r\theta\]

Nota

Es importante recordar que para calcular la longitud del arco, debemos medir el ángulo central en radianes.

(No está claro por qué\(s\) se suele utilizar la letra para representar la longitud del arco. Una explicación es que el arco “subtiende” un ángulo.)

Ejercicio\(\PageIndex{1}\)

Usando los círculos en la actividad inicial para esta sección:

1. Utilice la fórmula para la longitud del arco para determinar la longitud del arco en un círculo de radio de 10 pies que subtiende un ángulo central de\(\dfrac{\pi}{2}\) radianes. ¿El resultado es igual a una cuarta parte de la circunferencia del círculo?
2. Utilice la fórmula para la longitud del arco para determinar la longitud del arco en un círculo de radio de 20 pies que subtiende un ángulo central de\(\dfrac{\pi}{2}\) radianes. ¿El resultado es igual a una cuarta parte de la circunferencia del círculo?
3. Determine la longitud del arco en un círculo de radio 3 pies que está subtendido por un ángulo de\(22^\circ\).

Responder

1. Usa la fórmula\(s = r\theta\). \[s = r\theta = (10ft)\dfrac{\pi}{2}\]\[s = 5\pi\]La longitud del arco es\(5\pi\) pies.
2. Usa la fórmula\(s = r\theta\). \[s = r\theta = (20ft)\dfrac{\pi}{2}\]\[s = 5\pi\]La longitud del arco es\(10\pi\) pies.
3. Primero convertir\(22^\circ\) a radianes. Entonces\(\theta = 22^\circ \times (\dfrac{\pi rad}{180^\circ}) = \dfrac{11\pi}{90}\), y\[s = r\theta = (3ft)\dfrac{11\pi}{90}\]\[s = \dfrac{11\pi}{30}\] La longitud del arco es\(\dfrac{11\pi}{30}\) pies o aproximadamente\(1.1519\) pies.

¿Por qué Radianes?

La medida de grado es familiar y conveniente, entonces, ¿por qué introducimos la unidad de radián? Esta es una buena pregunta, pero una con una respuesta sutil. Como acabamos de ver, la longitud\(s\) de un arco sobre un círculo de radio\(r\) subtendido por ángulo de\(\theta\) radianes viene dada por\(s = r\theta\), entonces\(\theta = \dfrac{s}{r}\). Como resultado, un radián es una relación de dos longitudes (el cociente de la longitud de un arco por un radio de un círculo), lo que hace que un radián sea una cantidad adimensional. Así, una medición en radianes solo puede pensarse como un número real. Esto es conveniente para tratar la longitud del arco (y la velocidad angular como veremos pronto), y también será útil cuando estudiemos fenómenos periódicos en el Capítulo 2. Por esta razón, la medida radianes se usa universalmente en matemáticas, física e ingeniería en contraposición a los grados, porque cuando usamos la medida de grado, todas las formas tienen que tener en cuenta la dimensión de grado en los cómputos. Esto significa que la medida de radianes es en realidad más natural desde un punto de vista matemático que la medida de grado.

Velocidad lineal y angular

La conexión entre un arco sobre un círculo y el ángulo que subtiende medido en radianes nos permite definir cantidades relacionadas con el movimiento en un círculo. Los objetos que viajan a lo largo de trayectorias circulares exhiben dos tipos de velocidad: velocidad lineal y angular. Piensa en girar en un tiovivo. Si dejas caer un guijarro del borde de un tiovivo en movimiento, el guijarro no caerá directamente hacia abajo. En cambio, seguirá avanzando con la velocidad que tuvo el tiovivo en el momento en que se soltó el guijarro. Esta es la velocidad lineal del guijarro. La velocidad lineal mide cómo cambia la longitud del arco con el tiempo.

Considera un punto que\(P\) se mueve a una velocidad constante a lo largo de la circunferencia de un círculo de radio\(r\). A esto se le llama movimiento circular uniforme. Supongamos que P se mueve una distancia de s unidades en el tiempo\(t\). La velocidad lineal v del punto\(P\) es la distancia que recorrió dividida por el tiempo transcurrido. Es decir,\(v = \dfrac{s}{t}\). La distancia s es la longitud del arco y eso lo sabemos\(s = r\theta\).

Definición: velocidad lineal

Considera un punto que\(P\) se mueve a una velocidad constante a lo largo de la circunferencia de un círculo de radio\(r\). La velocidad lineal\(v\) del punto\(P\) viene dada por

\[v = \dfrac{s}{t} = \dfrac{r\theta}{t}\]

donde\(\theta\), medido en radianes, es el ángulo central subtendido por el arco de longitud\(s\).

Otra forma de medir qué tan rápido se mueve un objeto a una velocidad constante en una trayectoria circular se llama velocidad angular. Mientras que la velocidad lineal mide cómo cambia la longitud del arco con el tiempo, la velocidad angular es una medida de qué tan rápido cambia el ángulo central con el tiempo.

Definición: velocidad angular

Considera un punto P que se mueve con velocidad constante a lo largo de la circunferencia de un círculo de radio r sobre un arco que corresponde a un ángulo central de medida\(\theta\) (en radianes). La velocidad angular\(\omega\) del punto es la medida radianes del ángulo\(\theta\) dividida por el tiempo t que lleva barrer este ángulo. Eso es

\[\omega = \dfrac{\theta}{t}.\]

Nota

El símbolo\(\omega\) es la letra griega minúscula “omega”. Además, observe que la velocidad angular no depende del radio r.

Esta es una definición algo especializada de velocidad angular que es ligeramente diferente a un término común utilizado para describir qué tan rápido gira un punto alrededor de un círculo. Este término son revoluciones por minuto o rpm. En ocasiones se utilizan las revoluciones unitarias por segundo. Una mejor manera de representar las revoluciones por minuto es usar la “fracción unitaria”\(\dfrac{rev}{min}\). Ya que 1 revolución es\(2\pi\) radianes, vemos que si un objeto min se mueve a x revoluciones por minuto, entonces

\[\omega = x \dfrac{rev}{min} \cdot \dfrac{2\pi rad}{rev} = x(2\pi)\dfrac{rad}{min}.\]

Ejercicio\(\PageIndex{2}\)

Supongamos que un disco circular está rotando a una velocidad de 40 revoluciones por minuto. Deseamos determinar la velocidad lineal v (en pies por segundo) de un punto que está a 3 pies del centro del disco.

1. Determinar la velocidad angular\(\omega\) del punto en radianes por minuto. Pista: Usa la fórmula\[\omega = x \dfrac{rev}{min} \cdot \dfrac{2\pi rad}{rev}.\]
2. Ahora sabemos\(\omega = \dfrac{\theta}{t}\). Así que usa la fórmula\(v = \dfrac{r\theta}{t}\) para determinar\(v\) en pies por minuto.
3. Finalmente, convierta la velocidad lineal v en pies por minuto a pies por segundo.

Responder

1. Vemos que

\[\omega = 40\dfrac{rev}{min} \times \dfrac{2\pi\space rad}{rev}\]
\[\omega = 80\pi\dfrac{rad}{min}\]

2. El resultado de la parte (a) da

\[v = r(\dfrac{\theta}{r}) = r\omega\]
\[v = (3ft) \times 80\pi\dfrac{rad}{min}\]
\[v = 240\pi\dfrac{ft}{min}\]

3. Ahora convertimos pies por minuto en pies por segundo.

\[v = 240\pi\dfrac{ft}{min} \times \dfrac{1\space min}{60\space sec}\]
\[v = 4\pi\dfrac{ft}{sec} \approx 12.566\dfrac{ft}{sec}\]

Observe que en el Ejercicio 1.18, una vez que determinamos la velocidad angular, pudimos determinar la velocidad lineal. Lo que hicimos en este caso concreto lo podemos hacer en general. Existe una fórmula simple que relaciona directamente la velocidad lineal con la velocidad angular. Nuestra fórmula para la velocidad lineal es\(v =\dfrac{s}{t} \dfrac{r\theta}{t}\). Observe que podemos escribir esto es\(v = r\dfrac{\theta}{t}\). Es decir,\(v = r\omega\)

Nota

Considera un punto que\(P\) se mueve con velocidad constante (lineal)\(v\) a lo largo de la circunferencia de un círculo de radio\(r\). Si la velocidad angular es\(\omega\), entonces

\[v = r\omega\]

Entonces en el Ejercicio 1.18, una vez que determinamos eso\(\omega = 80\pi \dfrac{rad}{min}\), podríamos determinar v de la siguiente manera:

\[v = r\omega = (3\space ft)(80\pi\dfrac{rad}{min} = 240\pi\dfrac{ft}{min}).\]

Observe que dado que los radianes son “sin unidades”, podemos dejarlos caer cuando se trata de ecuaciones como la anterior.

Ejemplo\(\PageIndex{1}\): Linear and Angular Velocity

El disco de vinilo LP (long play) o 331 rpm es un medio de almacenamiento de sonido analógico y se ha utilizado durante mucho tiempo para escuchar música. Un LP suele tener 12 pulgadas o 10 pulgadas de diámetro. Para poder trabajar con nuestras fórmulas de velocidad lineal y angular, necesitamos conocer la velocidad angular en radianes por unidad de tiempo. Para ello, convertiremos\(33\dfrac{1}{3}\) revoluciones por minuto en radianes por minuto. Vamos a utilizar el hecho de que\(33\dfrac{1}{3} = \dfrac{100}{3}\)

\[\omega = \dfrac{100}{3}\dfrac{rev}{min} \times \dfrac{2\pi \space rad}{1\space rev} = \dfrac{200\pi}{3}\dfrac{rad}{min}\]

Ya podemos usar la fórmula v D r! para determinar la velocidad lineal de un punto en el borde de un LP de 12 pulgadas. El radio es de 6 pulgadas y así

\[v = r\omega = (6\space inches)(\dfrac{200\pi}{3}\dfrac{rad}{min}) = 400\pi \dfrac{inches}{min}\]

Podría ser más conveniente expresar esto como un valor decimal en pulgadas por segundo. Así conseguimos

\[v = 400\pi \dfrac{inches}{min} \times \dfrac{1\space min}{60 \space sec} \approx 20. 944\dfrac{inches}{sec}\]

La velocidad lineal es de aproximadamente 20.944 pulgadas por segundo.

Ejercicio\(\PageIndex{3}\)

Para estos problemas, asumiremos que la Tierra es una esfera con un radio de 3959 millas. A medida que la Tierra gira sobre su eje, una persona de pie sobre la Tierra viajará en un círculo que es perpendicular al eje.

1. La Tierra gira sobre su eje una vez cada\(24\) hora. Determinar la velocidad angular de la Tierra en radianes por hora. (Deja tu respuesta en términos del número ≡ ╳\(\pi\).)
2. A medida que la Tierra gira, una persona de pie en el ecuador viajará en un círculo cuyo radio es de 3959 millas. Determinar la velocidad lineal de esta persona en millas por hora.
3. A medida que la Tierra gira, una persona parada en un punto cuya latitud es el\(60^\circ\) norte viajará en un círculo de radio 2800 millas. Determinar la velocidad lineal de esta persona en millas por hora y pies por segundo.

Responder

1. Una revolución corresponde a\(2\pi\) radianes. Entonces\[\omega = \dfrac{2\pi\space rad}{24\space hr} = \dfrac{\pi\space rad}{12\space hr}.\]
2. Para determinar la velocidad lineal, utilizamos la fórmula\(v = r\omega\)\[v = r\omega = (3959mi)(\dfrac{\pi}{12}\dfrac{rad}{hr}) = \dfrac{3959\pi}{12}\dfrac{mi}{hr}\] La velocidad lineal es de aproximadamente 1036.5 millas por hora.
3. Para determinar la velocidad lineal, utilizamos la fórmula\(v = r\omega\)\[v = r\omega = (2800mi)(\dfrac{\pi}{12}\dfrac{rad}{hr}) = \dfrac{2800\pi}{12}\dfrac{mi}{hr}\] La velocidad lineal es de aproximadamente 733.04 millas por hora. Para convertir esto en pies por segundo, utilizamos los hechos de que hay 5280 pies en una milla, 60 minutos en una hora y 60 segundos en un minuto. Entonces

\[v = (\dfrac{2800\pi}{12}\dfrac{mi}{hr})(\dfrac{5280\space ft}{1\space mi})(\dfrac{1\space hr}{60\space min})(\dfrac{1\space min}{60\space sec}) = \dfrac{(2800\pi)(5280)}{12\cdot 60\cdot 60}\dfrac{ft}{sec}\]

Entonces la velocidad lineal es de aproximadamente\(1075.1\) pies por segundo.

Resumen

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

• En un círculo de radio\(r\), la longitud del arco\(s\) interceptada por un ángulo central con medida de radianes es\[s = r\theta\]
• El movimiento circular uniforme es cuando un punto se mueve a una velocidad constante a lo largo de la circunferencia de un círculo. La velocidad lineal es la longitud del arco recorrida por el punto dividida por el tiempo transcurrido. Mientras que la velocidad lineal mide cómo cambia la longitud del arco con el tiempo, la velocidad angular es una medida de qué tan rápido cambia el ángulo central con el tiempo. La velocidad angular del punto es la medida radianes del ángulo dividida por el tiempo que lleva barrer este ángulo.
• Para un punto que\(P\) se mueve con velocidad constante (lineal) v a lo largo de la circunferencia de un círculo de radio\(r\), tenemos\[v = r\omega\] donde\(\omega\) está la velocidad angular del punto.