1.5: Arcos comunes y arcos de referencia

Última actualización
Guardar como PDF

Page ID: 113351

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Preguntas de enfoque

Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

¿Cómo determinamos los valores para coseno y seno para arcos cuyos extremos están en el$x$ eje -eje o en el$y$ eje -eje?
¿Cuáles son los valores exactos de coseno y seno para$t = \dfrac{\pi}{6}, t = \dfrac{\pi}{4}$ y$t = \dfrac{\pi}{3}$?
¿Cuál es el arco de referencia para un arco dado? ¿Cómo determinamos el arco de referencia para un arco dado?
¿Cómo utilizamos los arcos de referencia para calcular los valores del coseno y seno en otros arcos que tienen$\dfrac{\pi}{6}, \dfrac{\pi}{4}$ o$t = \dfrac{\pi}{3}$ como arcos de referencia?

Actividad inicial

La figura$\PageIndex{1}$ muestra un círculo unitario con los puntos terminales para algunos arcos entre 0 y$2\pi$. Además, hay cuatro segmentos de línea dibujados en el diagrama que forman un rectángulo. Los segmentos de línea van desde: (1) el punto terminal$t = \dfrac{\pi}{6}$ para al punto terminal para$t = \dfrac{5\pi}{6}$;

(2) el punto terminal para$t = \dfrac{5\pi}{6}$ al punto terminal para$t = \dfrac{7\pi}{6}$;

(3) el punto terminal para$t = \dfrac{7\pi}{6}$ al punto terminal para$t = \dfrac{11\pi}{6}$;

y (4) el punto terminal$t = \dfrac{11\pi}{6}$ para el punto terminal para$t = \dfrac{\pi}{6}$;

¿Cuáles son los valores aproximados de$\cos(\dfrac{\pi}{6})$ y$\sin(\dfrac{\pi}{6})$?
¿Cuáles son los valores aproximados de$\cos(\dfrac{5\pi}{6})$ y$\sin(\dfrac{5\pi}{6})$?
¿Cuáles son los valores aproximados de$\cos(\dfrac{7\pi}{6})$ y$\sin(\dfrac{7\pi}{6})$?
¿Cuáles son los valores aproximados de$\cos(\dfrac{11\pi}{6})$ y$\sin(\dfrac{11\pi}{6})$?
Dibuje un rectángulo similar en la Figura 1.17 conectando los puntos terminales para$t = \dfrac{\pi}{4}$$t = \dfrac{3\pi}{4}$,$t = \dfrac{5\pi}{4}$, y$t = \dfrac{7\pi}{4}$. ¿Cómo se relacionan los valores de coseno y seno para estos arcos?

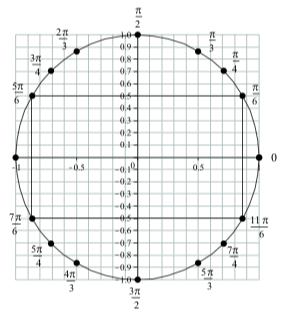
$1.17.png$

Figura$\PageIndex{1}$: Algunos arcos en el círculo unitario

Nuestra tarea en esta sección es determinar los valores coseno y seno exactos para todos los arcos cuyos puntos terminales se muestran en la Figura$\PageIndex{1}$. Primero notamos que ya conocemos los valores coseno y seno para los arcos cuyos puntos terminales están en uno de los ejes de coordenadas. Estos valores se muestran en la siguiente tabla.

Tabla 1.2: Valores de coseno y seno
$t$	0	$\dfrac{\pi}{2}$	$\pi$	$\dfrac{3\pi}{2}$	$2\pi$
\ (t\)” style="vertical-align:middle; ">$\cos(t)$	1	\ (\ dfrac {\ pi} {2}\)” style="vertical-align:middle; ">0	\ (\ pi\)” style="vertical-align:middle; ">-1	\ (\ dfrac {3\ pi} {2}\)” style="vertical-align:middle; ">0	\ (2\ pi\)” style="vertical-align:middle; ">1
\ (t\)” style="vertical-align:middle; ">$\sin(t)$	0	\ (\ dfrac {\ pi} {2}\)” style="vertical-align:middle; ">1	\ (\ pi\)” style="vertical-align:middle; ">0	\ (\ dfrac {3\ pi} {2}\)” style="vertical-align:middle; ">-1	\ (2\ pi\)” style="vertical-align:middle; ">0

El propósito de la actividad inicial fue mostrar que determinamos los valores de coseno y seno para los otros arcos encontrando solo los valores coseno y seno para los arcos cuyos puntos terminales se encuentran en el primer cuadrante. Entonces esta es nuestra primera tarea. Para ello, nos apoyaremos en algunos hechos sobre ciertos triángulos rectos. Los tres triángulos que usaremos se muestran en la Figura 1.18.

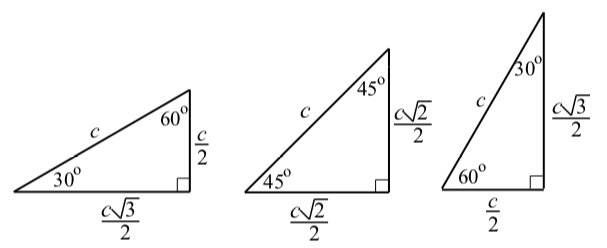
$1.18.png$

Figura$\PageIndex{2}$: Triángulos Retos Especiales.

En cada figura, la hipotenusa del triángulo rectángulo tiene una longitud de c unidades. Las longitudes de los otros lados se determinan utilizando el Teorema de Pitágoras. Una explicación de cómo se determinaron estas longitudes se puede encontrar en la página 420 del Apéndice C. La convención habitual es usar la medida de grado para los ángulos cuando trabajamos con triángulos, pero podemos convertir fácilmente estas medidas de grado en medidas de radianes.

Un$^\circ$ ángulo de 30 tiene una medida radianes de$\dfrac{\pi}{6}$ radianes.
Un$^\circ$ ángulo de 45 tiene una medida radianes de$\dfrac{\pi}{4}$ radianes.
Un$^\circ$ ángulo de 60 tiene una medida radianes de$\dfrac{\pi}{3}$ radianes.

Los valores del coseno y el seno en$t = \dfrac{\pi}{6}$

La figura$\PageIndex{3}$ muestra el círculo unitario en el primer cuadrante con un arco en posición estándar de longitud. El punto terminal del arco es el punto P y sus coordenadas son$(\cos(\dfrac{\pi}{6}), \sin(\dfrac{\pi}{6}))$. Entonces, desde el diagrama, vemos que

\[x = \cos(\dfrac{\pi}{6})\space and \space y = \sin(\dfrac{\pi}{6})\]

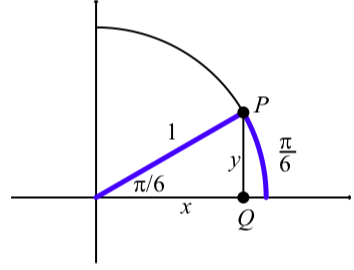
$1.19.png$

Figura$\PageIndex{3}$: El arco y su ángulo asociado

Como se muestra en el diagrama, formamos un triángulo rectángulo dibujando una línea desde$P$ que es perpendicular al$x$ eje -e intersecta el$x$ eje -en$Q$. Entonces en este triángulo rectángulo, el ángulo asociado con el arco es$\dfrac{\pi}{6}$ radianes o$30^\circ$. Por lo que sabemos de este tipo de triángulo rectángulo, el otro ángulo agudo en el triángulo rectángulo es$60^\circ$ o$\dfrac{\pi}{3}$ radianes. Entonces podemos usar los resultados que se muestran en el triángulo de la izquierda en la Figura$\PageIndex{2}$ para concluir que$x = \dfrac{\sqrt{3}}{2}$ y$y = \dfrac{1}{2}$. (Ya que en este caso,$c = 1$.) Por lo tanto, acabamos de demostrar que

\[\cos(\dfrac{\pi}{6} = \dfrac{\sqrt{3}}{2}) \space and \space \sin(\dfrac{\pi}{6}) = \dfrac{1}{2}\]

Ejercicio$\PageIndex{1}$

En la actividad inicial de esta sección, utilizamos el círculo unitario para aproximar los valores de las funciones coseno y seno en$t = \dfrac{\pi}{6}$,$t = \dfrac{5\pi}{6}$,$t = \dfrac{7\pi}{6}$, y$t = \dfrac{11\pi}{6}$. También vimos que todos estos valores están relacionados y que una vez que tenemos valores para las funciones coseno y seno en$t = \dfrac{\pi}{6}$, podemos usar nuestro conocimiento de los cuatro cuadrantes para determinar estos valores de función en$t = \dfrac{5\pi}{6}$,$t = \dfrac{7\pi}{6}$, y$t = \dfrac{11\pi}{6}$. Ahora que sabemos que\[\cos(\dfrac{\pi}{6}) = \dfrac{\sqrt{\pi}}{6} = \dfrac{1}{2},\]

determinar los valores exactos de cada uno de los siguientes:

$\cos(\dfrac{5\pi}{6})$y$\sin(\dfrac{5\pi}{6})$
$\cos(\dfrac{7\pi}{6})$y$\sin(\dfrac{7\pi}{6})$
$\cos(\dfrac{11\pi}{6})$y$\sin(\dfrac{11\pi}{6})$

Responder

$\cos(\dfrac{5\pi}{6}) = -\dfrac{\sqrt{3}}{2}$y$\sin(\dfrac{5\pi}{6}) = \dfrac{1}{2}$
$\cos(\dfrac{7\pi}{6}) = -\dfrac{\sqrt{3}}{2}$y$\sin(\dfrac{7\pi}{6}) = -\dfrac{1}{2}$
$\cos(\dfrac{11\pi}{6}) = -\dfrac{\sqrt{3}}{2}$y$\sin(\dfrac{11\pi}{6}) = -\dfrac{1}{2}$

Los valores del coseno y el seno en$t = \dfrac{\pi}{4}$

La figura$\PageIndex{4}$ muestra el círculo unitario en el primer cuadrante con un arco en posición estándar de longitud$\dfrac{\pi}{4}$. El punto terminal del arco es el punto$P$ y sus coordenadas son$(\cos(\dfrac{\pi}{4}), \sin(\dfrac{\pi}{4}))$. Entonces, desde el diagrama, vemos que

\[x = \cos(\dfrac{\pi}{4})\space and \space y = \sin(\dfrac{\pi}{4})\]

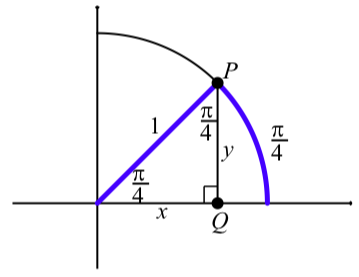
$1.20.png$

Figura$\PageIndex{4}$: El arco$\dfrac{\pi}{4}$ y su ángulo asociado.

Como se muestra en el diagrama, formamos un triángulo rectángulo dibujando una línea$P$ que es perpendicular al eje x e intersecta el eje x en$Q$. Entonces en este triángulo rectángulo, los ángulos agudos son$\dfrac{\pi}{4}$ radianes o$45^\circ$. Entonces podemos usar los resultados que se muestran en el triángulo en el centro de la Figura$\PageIndex{2}$ para concluir que$x = \dfrac{\sqrt{2}}{2}$ y$y = \dfrac{\sqrt{2}}{2}$. (Ya que en este caso,$c = 1$.) Por lo tanto, acabamos de demostrar que\[cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2} \space and \space sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}.\]

Ejercicio$\PageIndex{2}$

Ahora que sabemos que\[cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2} \space and \space sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}.\]

utilizar un método similar al utilizado en el Ejercicio 1.21 para determinar los valores exactos de cada uno de los siguientes:

$\cos(\dfrac{3\pi}{4}) \space and \space \sin(\dfrac{3\pi}{4}).$
$\cos(\dfrac{5\pi}{4}) \space and \space \sin(\dfrac{5\pi}{4}).$
$\cos(\dfrac{7\pi}{4}) \space and \space \sin(\dfrac{7\pi}{4}).$

Responder

$\cos(\dfrac{3\pi}{4}) = -\dfrac{\sqrt{2}}{2}$y$\sin(\dfrac{3\pi}{4}) = \dfrac{\sqrt{2}}{2}$
$\cos(\dfrac{7\pi}{6}) = -\dfrac{\sqrt{2}}{2}$y$\sin(\dfrac{7\pi}{6}) = -\dfrac{\sqrt{2}}{2}$
$\cos(\dfrac{11\pi}{6}) = \dfrac{\sqrt{2}}{2}$y$\sin(\dfrac{11\pi}{6}) = -\dfrac{\sqrt{2}}{2}$

Los valores del coseno y el seno en$t = \dfrac{\pi}{3}$

La figura$\PageIndex{4}$ muestra el círculo unitario en el primer cuadrante con un arco en posición estándar de longitud$\dfrac{\pi}{3}$. El punto terminal del arco es el punto P y sus coordenadas son$(\cos(\dfrac{\pi}{3}), \sin(\dfrac{\pi}{3}))$. Entonces, desde el diagrama, vemos que\[x = \cos(\dfrac{\pi}{3})\space and \space y = \sin(\dfrac{\pi}{3})\]

Como se muestra en el diagrama, formamos un triángulo rectángulo dibujando una línea desde$P$ que es perpendicular al eje x y se cruza con el$x$ eje -en$Q$. Entonces en este triángulo rectángulo, el ángulo asociado con el arco es$\dfrac{\pi}{3}$ radianes o$60^\circ$. Por lo que sabemos de este tipo de triángulo rectángulo, el otro ángulo agudo en el triángulo rectángulo es$30^\circ$

o$\dfrac{\pi}{6}$ radianes. Entonces podemos usar los resultados que se muestran en el triángulo de la derecha en la Figura$\PageIndex{5}$ para concluir eso$x= \dfrac{1}{2} \space and \space y = \dfrac{\sqrt{3}}{2}.$. (Ya que en este caso,$c = 1$.)

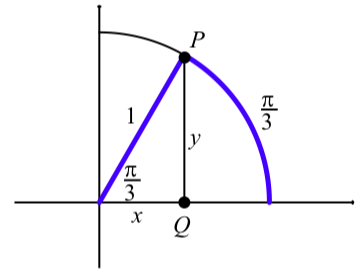
$1.21.png$

Figura$\PageIndex{5}$: El arco$\dfrac{\pi}{3}$ y su ángulo asociado.

Por lo tanto, acabamos de demostrar que\[\cos(\dfrac{\pi}{3}) = \dfrac{1}{2} \space and \space \sin(\dfrac{\pi}{3}) = \dfrac{\sqrt{3}}{2}.\]

Arcos de referencia (ángulos de referencia)

En la actividad inicial para esta sección y en los Ejercicios 1.21 y 1.22, vimos que podíamos relacionar las coordenadas del punto terminal de un arco de longitud mayor que$\dfrac{\pi}{2}$ en el círculo unitario con las coordenadas del punto terminal de un arco de longitud entre$0$ y$\dfrac{\pi}{2}$ sobre la unidad círculo. Esto se pretendía mostrar que podemos hacer esto para cualquier ángulo de longitud mayor que$\dfrac{\pi}{2}$, y esto significa que si conocemos los valores del coseno y seno para cualquier arco (o ángulo) entre$0$ y$\dfrac{\pi}{2}$, entonces podemos encontrar los valores del coseno y seno para cualquier arco en absoluto. El arco entre$0$ y con el$\dfrac{\pi}{2}$ que relacionamos un arco dado de longitud mayor que$\dfrac{\pi}{2}$ se denomina arco de referencia.

Definición

El arco de referencia$\hat{t}$ para un arco$t$ es el arco no negativo más pequeño (siempre considerado no negativo) entre el punto terminal del arco y la más cercana de las dos intercepciones x del círculo unitario. Tenga en cuenta que las dos intercepciones x del círculo unitario son$(-1, 0)$ y$(1, 0)$.

El concepto de arco de referencia se ilustra en la Figura$\PageIndex{6}$. Cada uno de los arcos más gruesos tiene longitud$\hat{t}$ y se puede ver que las coordenadas de los puntos en el segundo, tercer y cuarto cuadrantes están todas relacionadas con las coordenadas del punto en el primer cuadrante. Los signos de las coordenadas están todos determinados por el cuadrante en el que se encuentra el punto.

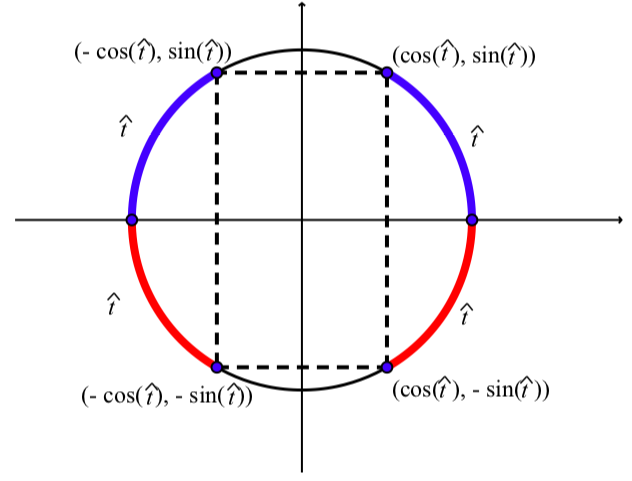
$1.22.png$

Figura$\PageIndex{6}$: Arcos de referencia.

La forma en que calculamos un arco de referencia para un arco de longitud dado$t$ depende del cuadrante en el que se$t$ encuentra el punto terminal de. Los diagramas de la Figura$\PageIndex{6}$ ilustran cómo calcular el arco de referencia para un arco de longitud t con$0 \leq t \leq 2\pi$.

En la Figura$\PageIndex{6}$, vemos que para un arco de longitud$t$ con$0 \leq t \leq 2\pi$:

Si$\dfrac{\pi}{2} < t < \pi$, entonces el punto que cruza el círculo unitario y el eje x que está más cerca del punto terminal de t es$(-1, 0)$. Entonces el arco de referencia es$\pi - t$. En este caso, la Figura$\PageIndex{6}$ muestra que\[\cos(\pi -t) = -\cos(t) \space and \space \sin(\pi -t) = \sin(t)\]
Si$\pi < t < \dfrac{\pi}{2}$, entonces el punto que cruza el círculo unitario y el eje x que está más cerca del punto terminal de t es$(-1, 0)$. Entonces el arco de referencia es$t - \pi$. En este caso, la Figura$\PageIndex{6}$ muestra que\[\cos(t - \pi) = -\cos(t) \space and \space \sin(t - \pi) = -\sin(t)\]
Si$\dfrac{3\pi}{2} < t < 2\pi$, entonces el punto que cruza el círculo unitario y el eje x que está más cerca del punto terminal de t es$(1, 0)$. Entonces el arco de referencia es$2\pi - t$. En este caso, la Figura$\PageIndex{6}$ muestra que\[\cos(2\pi -t) = \cos(t) \space and \space \sin(2\pi -t) = -\sin(t)\]

Ejercicio$\PageIndex{3}$

Para cada uno de los siguientes arcos, dibuje una imagen del arco en el círculo unitario. Luego determine el arco de referencia para ese arco y dibuje el arco de referencia en el primer cuadrante.

$t = \dfrac{5\pi}{4}$
$t = \dfrac{4\pi}{5}$
$t = \dfrac{5\pi}{3}$

Responder

Como se muestra en el siguiente diagrama:

El arco de referencia es$\dfrac{5\pi}{4} - \pi = \dfrac{\pi}{4}$. El arco de referencia es$\pi - \dfrac{4\pi}{5} = \dfrac{\pi}{5}$. El arco de referencia es$2\pi - \dfrac{5\pi}{3} = \dfrac{\pi}{3}$.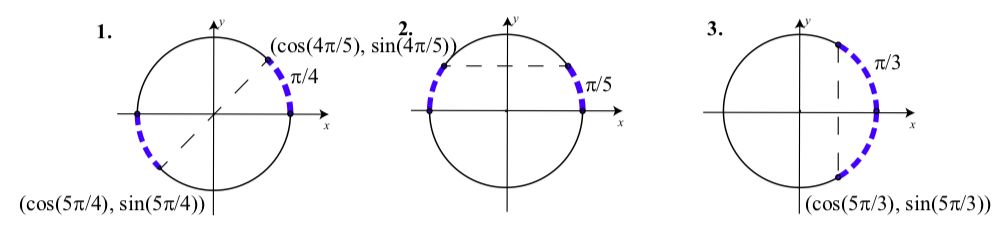

$1.23.png$

Ejercicio$\PageIndex{4}$

Si bien no usamos el término entonces, en los Ejercicios 1.21 y 1.22, utilizamos los hechos que$t = \dfrac{\pi}{6}$ y$t = \dfrac{\pi}{4}$ fueron los arcos de referencia para otros arcos para determinar los valores exactos de las funciones coseno y seno para esos otros arcos. Ahora use los valores de$\cos(\dfrac{\pi}{3})$ y$\sin(\dfrac{\pi}{3})$ para determinar los valores exactos de las funciones coseno y seno para cada uno de los siguientes arcos:

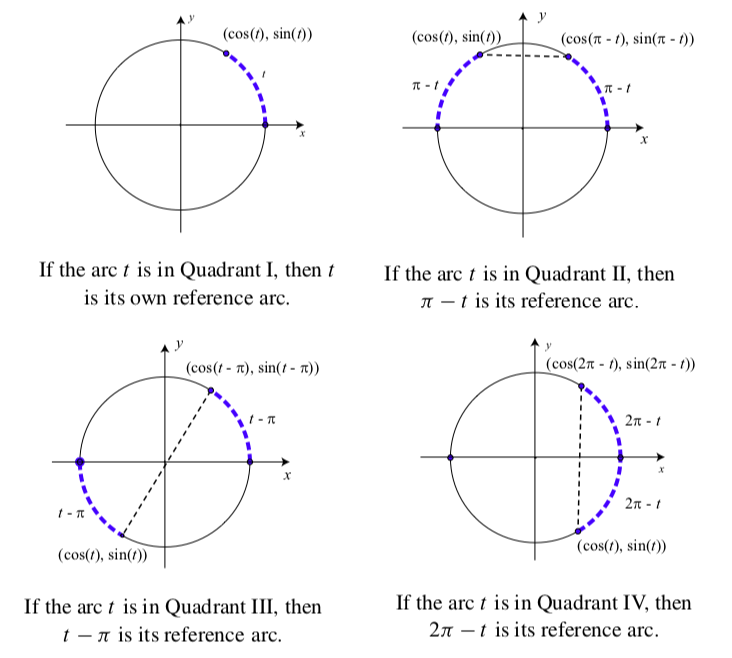
$1.23.png$

Figura$\PageIndex{7}$: Arcos de referencia

$t = \dfrac{2\pi}{3}$
$t = \dfrac{4\pi}{3}$
$t = \dfrac{5\pi}{3}$

Responder

$\cos(\dfrac{2\pi}{3}) = -\dfrac{1}{2}$y$\sin(\dfrac{2\pi}{3}) = \dfrac{\sqrt{3}}{2}$
$\cos(\dfrac{4\pi}{3}) = -\dfrac{1}{2}$y$\sin(\dfrac{4\pi}{3}) = -\dfrac{\sqrt{3}}{2}$
$\cos(\dfrac{5\pi}{3}) = \dfrac{1}{2}$y$\sin(\dfrac{5\pi}{3}) = -\dfrac{\sqrt{3}}{2}$

Arcos de Referencia para Arcos Negativos

Hasta ahora, solo hemos discutido arcos de referencia para arcos positivos, pero los mismos principios se aplican cuando usamos arcos negativos. Ya sea que el arco$t$ sea positivo o negativo, el arco de referencia para t es el arco no negativo más pequeño formado por el punto terminal de t y la intersección x más cercana del círculo unitario. Por ejemplo, para el arco$t = -\dfrac{\pi}{4}$ está en el cuarto cuadrante, y cuanto más cerca de las dos intercepciones x del círculo unitario está$(1, 0)$. Entonces el arco de referencia es$\hat{t} = \dfrac{\pi}{4}$ como se muestra en la Figura 1.24.

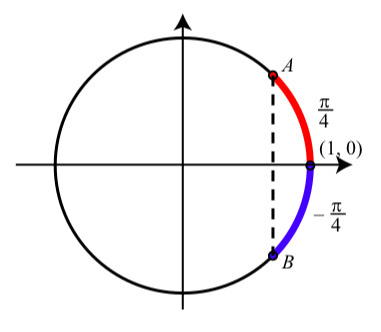
$1.24.png$

Figura$\PageIndex{8}$: Arco de referencia para$t = \dfrac{\pi}{4}$.

Como sabemos que el punto$A$ tiene coordenadas$(\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2})$, concluimos que el punto$B$ tiene coordenadas$(\dfrac{\sqrt{2}}{2}, -\dfrac{\sqrt{2}}{2})$, y así\[\cos(-\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2} \space and \space \sin(-\dfrac{\pi}{4}) = -\dfrac{\sqrt{2}}{2}.\]

Ejercicio$\PageIndex{5}$

Para cada uno de los siguientes arcos, determine el arco de referencia y los valores de las funciones coseno y seno.

$t = -\dfrac{\pi}{6}$
$t = -\dfrac{2\pi}{3}$
$t = -\dfrac{5\pi}{4}$

Responder

El punto terminal de$t = -\dfrac{\pi}{6}$ está en el cuarto cuadrante y el arco de referencia para$t = -\dfrac{\pi}{6}$ es$\hat{t} = \dfrac{\pi}{6}$. Entonces\[\cos(-\dfrac{\pi}{6}) = \dfrac{\sqrt{3}}{2}\] y\[\sin(-\dfrac{\pi}{6}) = -\dfrac{1}{2}\]
El punto terminal de$t = -\dfrac{2\pi}{3}$ está en el cuarto cuadrante y el arco de referencia para$t = -\dfrac{2\pi}{3}$ es$\hat{t} = \dfrac{\pi}{3}$. Entonces\[\cos(-\dfrac{2\pi}{3}) = -\dfrac{1}{2}\] y\[\sin(-\dfrac{2\pi}{3}) = -\dfrac{\sqrt{3}}{2}\]
El punto terminal de$t = -\dfrac{5\pi}{4}$ está en el cuarto cuadrante y el arco de referencia para$t = -\dfrac{5\pi}{4}$ es$\hat{t} = \dfrac{\pi}{4}$. Entonces\[\cos(-\dfrac{5\pi}{4}) = -\dfrac{\sqrt{2}}{2}\] y\[\sin(-\dfrac{5\pi}{4}) = -\dfrac{\sqrt{2}}{2}\]

Ejemplo$\PageIndex{1}$: (Using Reference Arcs)

En ocasiones podemos utilizar el concepto de arco de referencia aunque no sepamos la longitud del arco pero sí conocemos el valor de la función coseno o seno. Por ejemplo, supongamos que sabemos que\[0 < t < \dfrac{\pi}{2} \space and \space sin(t) = \dfrac{2}{3}.\]

¿Hay alguna conclusión que podamos sacar con esta información? A continuación se presentan algunas posibilidades.

Podemos utilizar la identidad pitagórica para determinar$\cos(t)$ de la siguiente manera:\[\cos^2(t) + \sin^2(t) = 1\]\[\cos^2(t) = 1 - \sin^2(t)\]\[\cos^2(t) = \dfrac{5}{9}\] Dado que t está en el primer cuadrante, sabemos que$\cos(t)$ es positivo, y por lo tanto\[\cos(t) = \sqrt{\dfrac{5}{9}} = \dfrac{\sqrt{5}}{3}\]
Ya que$0 < t < \dfrac{\pi}{2}$,$t$ está en el primer cuadrante. De ahí$\pi - t$ que esté en el segundo cuadrante y el arco de referencia lo esté$t$. En el segundo cuadrante sabemos que el seno es positivo, por lo que podemos concluir que\[\sin(\pi - t) = \sin(t) = \dfrac{2}{3}.\]

Ejercicio$\PageIndex{6}$

A continuación se presenta información del Ejemplo 1.26:\[0 < t < \dfrac{\pi}{2} \space and \space sin(t) = \dfrac{2}{3}.\] Utilice esta información para determinar los valores exactos de cada uno de los siguientes:

$\cos(\pi - t)$
$\sin(\pi + t)$
$\cos(\pi + t)$
$\sin(2\pi - t)$

Responder

Sabemos que$\pi - t$ está en el segundo cuadrante con arco de referencia$t$. Entonces\[\cos(\pi - t) = -\cos(t) = \dfrac{\sqrt{5}}{3}\]
El arco$\pi + t$ se encuentra en el segundo cuadrante con arco de referencia$t$. Entonces\[\sin(\pi + t) = -\sin(t) = -\dfrac{2}{3}\]
El arco$\pi + t$ se encuentra en el segundo cuadrante con arco de referencia$t$. Entonces\[\cos(\pi + t) = -\cos(t) = -\dfrac{\sqrt{5}}{3}\]
El arco$2\pi - t$ se encuentra en el segundo cuadrante con arco de referencia$t$. Entonces\[\sin(2\pi - t) = -\sin(t) = -\dfrac{2}{3}\]

Resumen

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

Los valores de$\cos(t)$ y$\sin(t)$ para arcos cuyos puntos terminales están en uno de los ejes de coordenadas se muestran en la Tabla 1.3 a continuación.
Los valores exactos para las funciones coseno y seno en$\dfrac{\pi}{6}$$\dfrac{\pi}{4}$, y$\dfrac{\pi}{3}$ son conocidos y se muestran en la Tabla 1.3 a continuación.
Un arco de referencia para un arco t es el arco (siempre considerado no negativo) entre el punto terminal del arco t y el punto que cruza el círculo unitario y el eje x más cercano a él.
Si$t$ es un arco que tiene un arco$\hat{t}$ como arco de referencia, entonces$|\cos(t)|$ y$|\cos(\hat{t})|$ son los mismos. Si$\cos(t) = \cos(\hat{t})$ o$\cos(t) = - \cos(\hat{t})$ está determinado por el cuadrante en el que se$t$ encuentra el lado terminal de. Lo mismo es cierto para$\sin(t)$
Podemos determinar los valores exactos de las funciones coseno y seno en cualquier arco con$\dfrac{\pi}{6}$$\dfrac{\pi}{4}$, o$\dfrac{\pi}{3}$ como arco de referencia. Estos arcos entre 0 y$2\pi$ se muestran en la Figura$\PageIndex{1}$. Los resultados se resumen en la Tabla 1.3 a continuación.

Cuadro 1.3: Valores exactos de las funciones coseno y seno.
$t$	0	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{3\pi}{4}$	$\dfrac{5\pi}{6}$	$\pi$	$\dfrac{7\pi}{6}$	$\dfrac{5\pi}{4}$	$\dfrac{4\pi}{3}$	$\dfrac{3\pi}{2}$	$\dfrac{5\pi}{3}$	$\dfrac{7\pi}{4}$	$\dfrac{11\pi}{6}$
$x=\cos(t)$	1	$\dfrac{\sqrt{3}}{2}$	$\dfrac{\sqrt{2}}{2}$	$\dfrac{1}{2}$	0	$-\dfrac{1}{2}$	$\dfrac{\sqrt{2}}{2}$	$\dfrac{\sqrt{3}}{2}$	-1	$-\dfrac{\sqrt{3}}{2}$	$-\dfrac{\sqrt{2}}{2}$	$-\dfrac{1}{2}$	0	$\dfrac{1}{2}$	$\dfrac{\sqrt{2}}{2}$	$\dfrac{\sqrt{3}}{2}$
$y=\sin(t)$	0	$\dfrac{1}{2}$	$\dfrac{\sqrt{2}}{2}$	$\dfrac{\sqrt{3}}{2}$	1	$\dfrac{\sqrt{3}}{2}$	$\dfrac{\sqrt{2}}{2}$	$\dfrac{1}{2}$	0	$-\dfrac{1}{2}$	$\dfrac{\sqrt{3}}{2}$	$-\dfrac{\sqrt{3}}{2}$	-1	$-\dfrac{\sqrt{3}}{2}$	$\dfrac{\sqrt{2}}{2}$	$-\dfrac{1}{2}$

\(t\)	0	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{2\pi}{3}\)	\(\dfrac{3\pi}{4}\)	\(\dfrac{5\pi}{6}\)	\(\pi\)	\(\dfrac{7\pi}{6}\)	\(\dfrac{5\pi}{4}\)	\(\dfrac{4\pi}{3}\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{5\pi}{3}\)	\(\dfrac{7\pi}{4}\)	\(\dfrac{11\pi}{6}\)
\(x=\cos(t)\)	1	\(\dfrac{\sqrt{3}}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{1}{2}\)	0	\(-\dfrac{1}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{\sqrt{3}}{2}\)	-1	\(-\dfrac{\sqrt{3}}{2}\)	\(-\dfrac{\sqrt{2}}{2}\)	\(-\dfrac{1}{2}\)	0	\(\dfrac{1}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{\sqrt{3}}{2}\)
\(y=\sin(t)\)	0	\(\dfrac{1}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{\sqrt{3}}{2}\)	1	\(\dfrac{\sqrt{3}}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{1}{2}\)	0	\(-\dfrac{1}{2}\)	\(\dfrac{\sqrt{3}}{2}\)	\(-\dfrac{\sqrt{3}}{2}\)	-1	\(-\dfrac{\sqrt{3}}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(-\dfrac{1}{2}\)