1.6: Otras funciones trigonométricas

Objetivos de aprendizaje

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Cómo se define la función tangente? ¿Cuál es el dominio de la función tangente?
• ¿Cuáles son las funciones recíprocas y cómo se definen? ¿Cuáles son los dominios de cada una de las funciones recíprocas?

Definimos las funciones coseno y seno como las coordenadas de los puntos terminales de los arcos en el círculo unitario. Como veremos más adelante, el seno y el coseno dan relaciones para ciertos lados y ángulos de triángulos rectos. Será útil poder relacionar diferentes lados y ángulos en triángulos rectos, y necesitamos otras funciones circulares para hacerlo. Obtenemos estas otras funciones circulares —tangente, cotangente, secante y cosecante— combinando el coseno y el seno de varias maneras.

Actividad inicial

Usando la medida de radián:

1. ¿Para qué valores de\(t\) es\(\cos(t) = 0\)?
2. ¿Para qué valores de\(t\) es\(\sin(t) = 0\)?
3. ¿En qué cuadrantes está\(\cos(t) > 0\)? ¿En qué cuadrantes está\(\sin(t) > 0\)?
4. ¿En qué cuadrantes está\(\cos(t) < 0\)? ¿En qué cuadrantes está\(\sin(t) < 0\)?

La función tangente

Junto al coseno y al seno, la función circular más útil es la tangente.

La palabra tangente fue introducida por Thomas Fincke (1561-1656) en su Flenspurgensis Geometriae rotundi libri XIII donde utilizó la palabra tangens en latín. Desde los primeros usos conocidos de algunas de las palabras de las matemáticas en http://jeff560.tripod.com/mathword.html.

Definición: función tangente

La función tangente es el cociente de la función sinusoidal dividido por la función coseno. Por lo que la tangente de un número real\(t\) se define para que sea\(\dfrac{\sin(t)}{\cos(t)}\) para aquellos valores\(t\) para los cuales\(\cos(t) \neq 0\). La abreviatura común para la tangente de\(t\) es

\[\tan(t) = \dfrac{\sin(t)}{\cos(t)}.\]

En esta definición, necesitamos la restricción que\(\cos(t) \neq 0\) para asegurarnos de que se defina el cociente. Ya\(\cos(t) \neq 0\) que siempre\(t = \dfrac{\pi}{2} + k\pi\) para algún entero\(k\), vemos que\(\tan(t)\) se define cuando\(t \neq \dfrac{\pi}{2} + k\pi\) para todos los enteros\(k\). Entonces el dominio de la función tangente es el conjunto de todos los números reales\(t\) para los cuales\(t \neq \dfrac{\pi}{2} + k\pi\) para cada entero\(k\). Observe que aunque el dominio de las funciones seno y coseno es todo números reales, esto no es cierto para la función tangente.

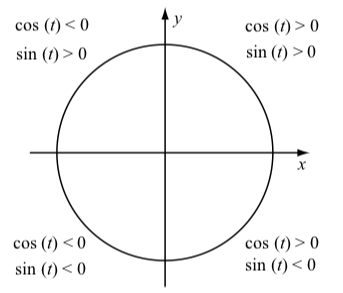
Cuando trabajamos con las definiciones de círculo unitario de coseno y seno, a menudo usamos el siguiente diagrama para indicar signos de\(\cos(t)\) y\(\sin(t)\) cuándo el punto terminal del arco t está en un cuadrante dado.

Ejercicio\(\PageIndex{1}\)

Considerando\(t\) que es un arco en el círculo unitario, para el punto terminal de\(t\):

1. ¿En qué cuadrantes es\(\tan(t)\) positivo?
2. ¿En qué cuadrantes es\(\tan(t)\) negativo?
3. ¿Para qué valores de\(t\) es\(tan(t) = 0\)?
4. Completa la Tabla 1.4, que da los valores de coseno, seno y tangente en los arcos de referencia comunes en el Cuadrante I.

Tabla 1.4: Valores de la Función Tangente

\(t\)	\(\cos(t)\)	\(\sin(t)\)	\(\tan(t)\)
\ (t\) ">0	\ (\ cos (t)\) ">	\ (\ sin (t)\) ">0	\ (\ tan (t)\) ">
\ (t\) ">\(\dfrac{\pi}{6}\)	\ (\ cos (t)\) ">	\ (\ sin (t)\) ">\(\dfrac{1}{2}\)	\ (\ tan (t)\) ">
\ (t\) ">\(\dfrac{\pi}{4}\)	\ (\ cos (t)\) ">	\ (\ sin (t)\) ">\(\dfrac{\sqrt{2}}{2}\)	\ (\ tan (t)\) ">
\ (t\) ">\(\dfrac{\pi}{4}\)	\ (\ cos (t)\) ">	\ (\ sin (t)\) ">\(\dfrac{\sqrt{3}}{2}\)	\ (\ tan (t)\) ">
\ (t\) ">\(\dfrac{\pi}{2}\)	\ (\ cos (t)\) ">	\ (\ sin (t)\) ">1	\ (\ tan (t)\) ">

Contestar

1. Ya que\(\tan(t) = \dfrac{\sin(t)}{\cos(t)}\),\(\tan(t)\) positivo cuando ambos\(\sin(t)\) y\(\cos(t)\) tienen el mismo signo. Entonces,\(\tan(t) > 0\) en los cuadrantes primero y tercero.
2. Vemos ese\(\tan(t)\) negativo cuando\(\sin(t)\) y\(\cos(t)\) tenemos signos opuestos. Entonces,\(\tan(t) < 0\) en los cuadrantes segundo y cuarto.
3. \(\tan(t)\)será cero cuando\(\sin(t) = 0\) y\(\cos(t) \neq 0\). Entonces,\(\tan(t) = 0\) cuando el punto terminal de\(t\) está en el\(x\) eje -. Es decir,\(\tan(t) = 0\) cuando\(t = k\pi\) para algún entero\(k\).
4. A continuación se presenta una versión terminada de la Tabla 1.4.

\(t\)	\(\cos(t)\)	\(\sin(t)\)	\(\tan(t)\)
\ (t\) ">\(0\)	\ (\ cos (t)\) ">\(1\)	\ (\ sin (t)\) ">\(0\)	\ (\ tan (t)\) ">\(0\)
\ (t\) ">\(\dfrac{\pi}{6}\)	\ (\ cos (t)\) ">\(\dfrac{\sqrt{3}}{2}\)	\ (\ sin (t)\) ">\(\dfrac{1}{2}\)	\ (\ tan (t)\) ">\(\dfrac{1}{\sqrt{3}}\)
\ (t\) ">\(\dfrac{\pi}{4}\)	\ (\ cos (t)\) ">\(\dfrac{\sqrt{2}}{2}\)	\ (\ sin (t)\) ">\(\dfrac{\sqrt{2}}{2}\)	\ (\ tan (t)\) ">\(1\)
\ (t\) ">\(\dfrac{\pi}{4}\)	\ (\ cos (t)\) ">\(\dfrac{1}{2}\)	\ (\ sin (t)\) ">\(\dfrac{\sqrt{3}}{2}\)	\ (\ tan (t)\) ">\(\sqrt{3}\)
\ (t\) ">\(\dfrac{\pi}{2}\)	\ (\ cos (t)\) ">\(0\)	\ (\ sin (t)\) ">\(1\)	\ (\ tan (t)\) ">indefinido

Al igual que con el coseno y el seno, si conocemos los valores de la función tangente en los arcos de referencia, podemos encontrar sus valores en cualquier arco relacionado con un arco de referencia. Por ejemplo, el arco de referencia para el arco\(t = \dfrac{5\pi}{3}\) es\(\dfrac{\pi}{3}\).

\[\tan(\dfrac{5\pi}{3}) = \dfrac{\sin(\dfrac{5\pi}{3})}{\cos(\dfrac{5\pi}{3})} = -\dfrac{\sin(\dfrac{\pi}{3})}{\cos(\dfrac{\pi}{3})} = \dfrac{-\dfrac{\sqrt{3}}{2}}{\dfrac{1}{2}} = -\sqrt{3}\]

Entonces podemos acortar este proceso con tan solo usar el hecho de que\(\tan(\dfrac{\pi}{3}) = \sqrt{3}\) y eso\(\tan(\dfrac{5\pi}{3}) < 0\) ya que el punto terminal del arco\(\dfrac{5\pi}{3}\) está en el cuarto cuadrante. \[\tan(\dfrac{5\pi}{3}) = -\tan(\dfrac{\pi}{3}) = -\sqrt{3}\]

Ejercicio\(\PageIndex{2}\)

1. Determinar los valores exactos de\(t = \dfrac{5\pi}{4}\) y\(t = \dfrac{5\pi}{6}\).
2. Determinar los valores exactos de\(\cos(t)\) y\(\tan(t)\) si se sabe que\(\sin(t) = \dfrac{1}{3}\) y\(\tan(t) < 0\).

Contestar

1. \[\tan(\dfrac{5\pi}{4}) = \tan(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}\]\[\tan(\dfrac{6\pi}{6}) = -\tan(\dfrac{\pi}{6}) = -\dfrac{1}{\sqrt{3}}\]

2. Primero usamos la Identidad Pitagórica. \[\cos^{2}(t) + \sin^{2}(t) = 1\]\[\cos^{2}(t) + (\dfrac{1}{3})^{2} = 1\]\[\cos^{2}(t) = \dfrac{8}{9}\]

Desde\(\sin(t) > 0\) y\(\tan(t) < 0\), concluimos que el punto terminal de\(t\) debe estar en el segundo cuadrante, y por lo tanto,,\(\cos(t) < 0\). Por lo tanto,

\[\cos(t) = -\dfrac{\sqrt{8}}{3}\]\[\tan(t) = \dfrac{\dfrac{1}{3}}{-\dfrac{\sqrt{8}}{3}} = -\dfrac{1}{\sqrt{8}}\]

Las funciones recíprocas

Las funciones circulares o trigonométricas restantes son recíprocas de las funciones coseno, seno y tangente. Dado que estas funciones son recíprocas, sus dominios serán todos números reales para los cuales el denominador no es igual a cero. El primero que vamos a introducir es la función secante.

Definición: función secante

La función secante es la recíproca de la función coseno. Entonces la secante de un número real\(t\) se define para que sea\(\dfrac{1}{\cos(t)}\) para aquellos valores\(t\) donde\(\cos(t) \neq 0\). La abreviatura común para la secante de\(t\) es\[\sec(t) = \dfrac{1}{\cos(t)}.\]

Dado que la función tangente y la función secante usan\(\cos(t)\) en un denominador, tienen el mismo dominio. Entonces el dominio de la función secante es el conjunto de todos los números reales\(t\) para los cuales\(t \neq \dfrac{\pi}{2} + k\pi\) para cada entero\(k\).

El término secante fue introducido por fue por Thomas Fincke (1561-1656) en su Thomae Finkii Flenspurgensis Geometriae rotundi libri XIII, Basileae: Per Sebastianum Henricpetri, 1583. Vieta (1593) no aprobó el término secante, creyendo que podría confundirse con el término geometría. En su lugar utilizó Transsinuosa. Desde los primeros usos conocidos de algunas de las palabras de las matemáticas en http://jeff560.tripod.com/mathword.html.

El siguiente es la función cosecante.

Definición: función cosecante

La función cosecante es la recíproca de la función secante. Entonces el cosecante de un número real\(t\) se define para que sea\(\dfrac{1}{\sin(t)}\) para esos valores t donde\(\sin(t) \neq 0\). La abreviatura común para la secante de\(t\) es\[\csc(t) = \dfrac{1}{\sin(t)}.\]

Ya\(\sin(t) = 0\) que siempre\(t = k\pi\) para algún entero\(k\), vemos que el dominio de la función cosecante es el conjunto de todos los números reales t para los cuales\(t \neq k\pi\) para cada entero\(k\).

Finalmente, tenemos la función cotangente.

Definición: función cotangente

La función cotangente es la recíproca de la función secante. Entonces la cotangente de un número real\(t\) se define para que sea\(\dfrac{1}{\tan(t)}\) para esos valores t donde\(\tan(t) \neq 0\). La abreviatura común para la secante de\(t\) es\[\cot(t) = \dfrac{1}{\tan(t)}.\]

Ya\(\tan(t) = 0\) que siempre\(t = k\pi\) para algún entero\(k\), vemos que el dominio de la función cotangente es el conjunto de todos los números reales\(t\) para los cuales\(t \neq k\pi\) para cada entero\(k\).

Georg Joachim von Lauchen Rheticus parece ser el primero en utilizar el término cosecante (como cosecanos en latín) en su Opus Palatinum de triangulis. Desde los primeros usos conocidos de algunas de las palabras de las matemáticas en http://jeff560.tripod.com/mathword.html.

La palabra cotangente fue introducida por Edmund Gunter en Canon Triangulorum (Tabla de Senos Artificiales y Tangentes) donde utilizó el término cotangens en latín. Desde los primeros usos conocidos de algunas de las palabras de las matemáticas en http://jeff560.tripod.com/mathword.html.

Una nota sobre las calculadoras

Cuando no es posible determinar valores exactos de una función trigonométrica, utilizamos una calculadora para determinar valores aproximados. Sin embargo, tenga en cuenta que muchas calculadoras solo tienen claves para las funciones seno, coseno y tangente. Con estas calculadoras, debemos usar las definiciones de cosecante, secante y cotangente para determinar valores aproximados para estas funciones.

Ejercicio\(\PageIndex{3}\)

Cuando sea posible, encuentre el valor exacto de cada uno de los siguientes valores funcionales. Cuando esto no sea posible, utilice una calculadora para encontrar una aproximación decimal a cuatro decimales.

1. \(\sec(\dfrac{7\pi}{4})\)
2. \(\csc(\dfrac{-\pi}{4})\)
3. \(\tan(\dfrac{7\pi}{8})\)
4. \(\cot(\dfrac{4\pi}{3})\)
5. \(\csc(5)\)

Contestar

1. \[\sec(\dfrac{7\pi}{4}) = \dfrac{1}{\cos(\dfrac{7\pi}{4})} = \dfrac{1}{\cos(\dfrac{\pi}{4})} = \dfrac{2}{\sqrt{2}} = \sqrt{2}\]
2. \[\csc(-\dfrac{\pi}{4}) = \dfrac{1}{\sin(-\dfrac{\pi}{4})} = \dfrac{1}{\sin(-\dfrac{\pi}{4})} = -\dfrac{2}{\sqrt{2}} = -\sqrt{2}\]
3. \[\tan(\dfrac{7\pi}{8}) \approx -0.4142\]
4. \[\cot(\dfrac{4\pi}{3}) = \cot(\dfrac{\pi}{3}) = \dfrac{1}{\tan(\dfrac{\pi}{3})} = \dfrac{2}{\sqrt{3}}\]
5. \[\csc(5) = \dfrac{1}{\sin(5)} \approx -1.0428\]

Ejercicio\(\PageIndex{4}\)

1. Si\(\cos(t) = \dfrac{1}{3}\) y\(\sin(t) < 0\), determinar los valores exactos de\(\sin(t)\),\(\tan(t)\),\(\csc(t)\), y\(\cot(t)\).
2. Si\(\sin(t) = \dfrac{-7}{10}\) y\(\tan(t) > 0\), determinar los valores exactos de\(\cos(t)\) y\(\cot(t)\).
3. ¿Cuál es otra forma de escribir\((\tan(t))(\cos(t))\)?

Contestar

1. Si\(\cos(x) = \dfrac{1}{3}\) y\(\sin(x) < 0\), utilizamos la Identidad Pitagórica para determinarlo\(\sin(x) = -\dfrac{\sqrt{8}}{3}\). Entonces podemos determinar que

\[\tan(x) = -\sqrt{8}\]\[\csc(x) = -\dfrac{3}{\sqrt{8}}\]\[\cot(t) = -\dfrac{1}{\sqrt{8}}\]

2. Si\(\sin(x) = -0.7\) y\(\tan(x) > 0\), utilizamos la Identidad Pitagórica para obtener\[\cos^{2}(x) + (-0.7)^{2} = 1\]\[\cos^{2}(x) = 0.51\]

Ya que también se nos da eso\(\tan(x) > 0\), sabemos que el punto terminal ofx está en el tercer cuadrante. Por lo tanto,\(\cos(x) < 0\) y\(\cos(x) = -\sqrt{0.51}\). Por lo tanto,

\[\tan(x) = \dfrac{-0.7}{-\sqrt{0.51}}\]\[\cot(x) = \dfrac{\sqrt{0.51}}{0.7}\]

3. Podemos utilizar la definición de\(\tan(x)\) para obtener\[(\tan(x))(\cos(x)) = \dfrac{\sin(x)}{\cos(x)}\cdot \cos(x) = \sin(x)\]

Entonces\(\tan(x)\cos(x) = \sin(x)\), pero hay que señalar que esta ecuación sólo es válida para aquellos valores de\(x\) para los que\(\tan(x)\) se define. Es decir, esta ecuación sólo es válida si no\(x\) es un múltiplo entero de\(\pi\).

Resumen

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

• La función tangente es el cociente de la función sinusoidal dividido por la función coseno. Así es el cociente de la función sinusoidal dividido por la función coseno. Es decir,\(\tan(t) = \dfrac{sin(t)}{\cos(t)}\) para aquellos valores\(t\) para los cuales\(\cos(t) \neq 0\). El dominio de la función tangente es el conjunto de todos los números reales\(t\) para los cuales\(t \neq \dfrac{\pi}{2} + k\pi\) para cada entero\(k\).
• Las funciones recíprocas son las funciones secante, cosecante y tangente.

Función Recíproca	Dominio
\(\sec(t) = \dfrac{1}{\cos(t)}\)	El conjunto de todos los números reales\(t\) para los cuales\(t \neq \dfrac{\pi}{2} + k\pi\) para cada entero\(k\)
\(\csc(t) = \dfrac{1}{\sin(t)}\)	El conjunto de todos los números reales t para los cuales\(t \neq k\pi\) para cada entero\(k\).
\(\cot(t) = \dfrac{1}{\tan(t)}\)	El conjunto de todos los números reales t para los cuales\(t \neq k\pi\) para cada entero\(k\).