1.E: Las Funciones Trigonométricas (Ejercicios)

Ejercicio\(\PageIndex{1}\)

El siguiente diagrama muestra ocho puntos trazados en el círculo unitario. Estos puntos corresponden a los siguientes valores cuando la recta numérica se envuelve alrededor del círculo unitario.

\(t = 1, t = 2, t = 3, t = 4, t = 5, t = 6, t = 7\), y\(t = 9\).

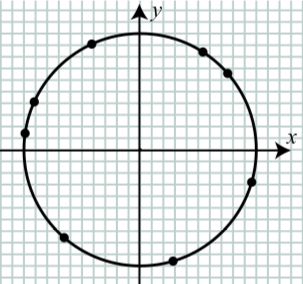
Figura\(\PageIndex{1}\)

(a) Etiquetar cada punto del diagrama con su valor de\(t\).

b) Aproximar las coordenadas de los puntos correspondientes a\(t = 1, t = 5\), y\(t=9\).

Contestar

\(t\)	punto
\ (t\) ">\(1\)	\((0.54, 0.84)\)
\ (t\) ">\(5\)	\((0.28, -0.96)\)
\ (t\) ">\(9\)	\((-0.91, 0.41)\)

Ejercicio\(\PageIndex{2}\)

El siguiente diagrama muestra los puntos correspondientes\(t = \dfrac{\pi}{5}\) y\(t = \dfrac{2\pi}{5}\) cuándo la recta numérica se envuelve alrededor del círculo unitario.

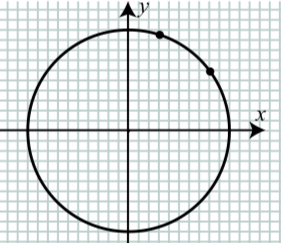
Figura\(\PageIndex{2}\)

En este círculo unitario, dibuje los puntos correspondientes a\(t = \dfrac{4\pi}{5}\),\(t = \dfrac{5\pi}{6}\),\(t = \dfrac{8\pi}{5}\) y\(t = \dfrac{10\pi}{5}\).

Contestar

Agrega textos aquí. No elimine primero este texto.

Ejercicio\(\PageIndex{3}\)

Dibuja los siguientes arcos en el círculo unitario.

(a) El arco que está determinado por el intervalo\([0, \dfrac{\pi}{6}]\) en la recta numérica.

b) El arco que está determinado por el intervalo\([0, \dfrac{7\pi}{6}]\) en la recta numérica.

(c) El arco que está determinado por el intervalo\([0, -\dfrac{\pi}{3}]\) en la recta numérica.

d) El arco que está determinado por el intervalo\([0, -\dfrac{4\pi}{5}]\) en la recta numérica.

Contestar

Agrega textos aquí. No elimine primero este texto.

Ejercicio\(\PageIndex{4}\)

Determinar el cuadrante que contiene el punto terminal de cada arco dado con punto inicial\((1, 0)\) en el círculo unitario.

(a)\(\dfrac{7\pi}{4}\)

b)\(\dfrac{-7\pi}{4}\)

c)\(\dfrac{5\pi}{3}\)

(d)\(\dfrac{-5\pi}{3}\)

(e)\(\dfrac{7\pi}{3}\)

f)\(\dfrac{-7\pi}{3}\)

(g)\(\dfrac{5\pi}{8}\)

(h)\(\dfrac{-5\pi}{8}\)

(i)\(2.5\)

(j)\(-2.5\)

k\(3\)) l\(3+2\pi\)

(m)\(3-\pi\)

(n)\(3-2\pi\)

Contestar

	\((a)\)	\((b)\)	\((d)\)	\((i)\)	\((j)\)	\((l)\)	\((m)\)
\(t\)	\ ((a)\)” class="lt-matemática-17332">\(\dfrac{7\pi}{4}\)	\ ((b)\)” class="lt-matemática-17332">\(-\dfrac{7\pi}{4}\)	\ ((d)\)” class="lt-matemática-17332">\(-\dfrac{3\pi}{5}\)	\ ((i)\)” class="lt-matemática-17332">\(2.5\)	\ ((j)\)” class="lt-matemática-17332">\(-2.5\)	\ ((l)\)” class="lt-matemática-17332">\(3 + 2\pi\)	\ ((m)\)” class="lt-matemática-17332">\(3 - \pi\)
Cuadrante	\ ((a)\)” class="LT-MATH-17332">IV	\ ((b)\)” class="LT-MATH-17332">I	\ ((d)\)” class="LT-MATH-17332">III	\ ((i)\)” class="LT-MATH-17332">II	\ ((j)\)” class="LT-MATH-17332">III	\ ((l)\)” class="LT-MATH-17332">II	\ ((m)\)” class="LT-MATH-17332">IV

Ejercicio\(\PageIndex{5}\)

Encuentra todos los puntos en el círculo de unidades:

(a) Cuya coordenada x es\(\dfrac{1}{3}\)

(b) Cuya coordenada y es\(-\dfrac{1}{2}\)

c) Cuya coordenada x es\(-\dfrac{3}{5}\)

(d) Cuya coordenada\(-\dfrac{3}{4}\) y cuya\(x\) coordenada es negativa.

Agrega texto aquí. Para que el número automático funcione, es necesario agregar la plantilla “AutoNum” (preferiblemente al final) a la página.

Contestar

(a) Sustituimos\(x = \dfrac{1}{3}\) en la ecuación\(x^{2} + y^{2} = 1\). Resolviendo para\(y\), obtenemos\(y = \pm\dfrac{\sqrt{8}}{3}\). Entonces los puntos son\((\dfrac{1}{3}, \dfrac{\sqrt{8}}{3})\) y\((\dfrac{1}{3}, -\dfrac{\sqrt{8}}{3})\).

(b) Sustituimos\(y = -\dfrac{1}{2}\) en la ecuación\(x^{2} + y^{2} = 1\). Resolviendo para\(x\), obtenemos\(x = \pm\dfrac{\sqrt{3}}{3}\). Entonces los puntos son\((\dfrac{\sqrt{8}}{3}, -\dfrac{1}{3})\) y\((-\dfrac{\sqrt{3}}{3}, -\dfrac{1}{2})\).

Ejercicio\(\PageIndex{6}\)

Rellene los espacios en blanco para cada uno de los siguientes:

1. Para un número real\(t\), el valor de\(\cos(t)\) se define como la () - coordenada del punto () de un arco t cuyo punto inicial es () en el () cuya ecuación es\(x^2 + y^2 = 1\).
2. El dominio de la función coseno es ().
3. El valor máximo de\(\cos(t)\) es () y esto ocurre en\(t\) = () para\(0 \leq t < 2\pi\). El valor mínimo de\(\cos(t)\) es () y esto ocurre en\(t\) = () para\(0 \leq t < 2\pi\).
4. El rango de la función coseno es ().

Contestar

1. Para un número real\(t\), el valor de\(\cos(t)\) se define como la coordenada x del punto terminal de un arco\(t\) cuyo punto inicial está \((1, 0)\)en el círculo unitario cuya ecuación es\(x^{2} + y^{2} = 1\).

2. El dominio de la función coseno es el conjunto de todos los números reales.

3. El valor máximo de\(\cos(t)\) es 1 y esto ocurre en\(t =\) 0 para\(1 \leq t < 2\pi\). El valor mínimo de\(\cos(t)\) es -1 y esto ocurre en\(t = \pi\) for\(0 \leq t < 2\pi\).

4. El rango de la función coseno es el intervalo cerrado\([-1,1]\).

Ejercicio\(\PageIndex{7}\)

Rellene los espacios en blanco para cada uno de los siguientes:

1. Para un número real\(t\), el valor de sin\((t)\) se define como la () - coordenada del punto () de un arco t cuyo punto inicial es () en el () cuya ecuación es\(x^2 + y^2 = 1\).
2. El dominio de la función sinusoidal es ().
3. El valor máximo de\(\sin(t)\) es () y esto ocurre en\(t\) = () para\(0 \leq t < 2\pi\). El valor mínimo de\(\sin(t)\) es () y esto ocurre en\(t\) = () para\(0 \leq t < 2\pi\).
4. El rango de la función sinusoidal es ().

Contestar

(a)\(\cos(t) = \dfrac{4}{5}\) o\(\cos(-\dfrac{4}{5})\).

c)\(\sin(t) = -\dfrac{-\sqrt{5}}{3}\).

Ejercicio\(\PageIndex{8}\)

• Complete la siguiente tabla de valores:

Longitud del arco en el círculo unitario	Punto terminal del arco	\(\cos(t)\)	\(\sin(t)\)
\(0\)	\((1, 0)\)	\(1\)	\(0\)
\(\dfrac{\pi}{2}\)
\(\pi\)
\(\dfrac{3\pi}{2}\)
\(2\pi\)

• Complete la siguiente tabla de valores:

Longitud del arco en el círculo unitario	Punto terminal del arco	\(\cos(t)\)	\(\sin(t)\)
\(0\)	\((1, 0)\)	\(1\)	\(0\)
\(-\dfrac{\pi}{2}\)
\(-\pi\)
\(-\dfrac{3\pi}{2}\)
\(-2\pi\)

• Complete la siguiente tabla de valores:

Longitud del arco en el círculo unitario	Punto terminal del arco	\(\cos(t)\)	\(\sin(t)\)
\(2\pi\)	\((1, 0)\)	\(1\)	\(0\)
\(\dfrac{5\pi}{2}\)
\(3\pi\)
\(\dfrac{7\pi}{2}\)
\(4\pi\)

Ejercicio\(\PageIndex{9}\)

1. ¿Cuáles son los valores posibles de\(\cos(t)\) si se sabe que\(\sin(t) = \dfrac{3}{5}\)?
2. ¿Cuáles son los valores posibles de\(\cos(t)\) si se sabe que\(\sin(t) = \dfrac{3}{5}\) y el punto terminal de\(t\) está en el segundo cuadrante?
3. ¿Cuál es el valor de\(\sin(t)\) si se sabe que\(\cos(t) = \dfrac{-2}{3}\) y el punto terminal de\(t\) está en el tercer cuadrante?

Ejercicio\(\PageIndex{10}\)

Supongamos que se sabe eso\(0 < \cos(t) < \dfrac{1}{3}\).

1. Al cuadrar las expresiones en las desigualdades dadas, ¿qué conclusiones se pueden sacar\(\cos^2(t)\)?
2. Utilice la parte (a) para escribir desigualdades que involucran\(-\cos^2(t)\) y luego desigualdades que involucran\(1 - \cos^2(t)\).
3. Usando la identidad pitagórica, vemos eso\(\sin^2(t) = 1 - \cos^2(t)\). Escribir la última desigualdad en la parte (b) en términos de\(\sin^2(t)\).
4. Si también lo sabemos\(\sin(t) > 0\), ¿qué podemos concluir ahora sobre el valor de\(\sin(t)\)?

Contestar

(a)\(0 < \cos^{2}(t) < \dfrac{1}{9}\).

b)\(-\dfrac{1}{9} < -\cos^{2}(t) < 0\) y así\(\dfrac{8}{9} < 1 - \cos^{2}(t) < 1\)

c)\(\dfrac{8}{9} < \sin^{2}(t) < 1\)

(d)\(\dfrac{\sqrt{8}}{3} < \sin(t) < 1\)

Ejercicio\(\PageIndex{11}\)

Utilice un proceso similar al del ejercicio (5) para completar cada uno de los siguientes:

1. Supongamos que se sabe eso\(-\dfrac{1}{4} < sin(t) < 0\) y aquello\(\cos(t) > 0\). ¿De qué se puede concluir\(\cos(t)\)?
2. Supongamos que se sabe eso\( 0 \leq \sin(t) \leq \dfrac{3}{7}\) y aquello\(\cos(t) < 0\). ¿De qué se puede concluir\(\cos(t)\)?

Ejercicio\(\PageIndex{12}\)

Usando las aproximaciones de cuatro dígitos para los valores de coseno y seno en el Ejercicio 1.6, calcule cada uno de los siguientes:

1. \(\cos^2(1) + \sin^2(1)\)
2. \(\cos^2(2) + \sin^2(2)\)
3. \(\cos^2(-4) + \sin^2(-4)\)
4. \(\cos^2(15) + \sin^2(15)\)

¿Cuál debería ser el valor exacto de cada uno de estos cálculos? ¿Por qué los resultados no son iguales a este valor exacto?

Ejercicio\(\PageIndex{13}\)

Convierta cada una de las siguientes mediciones de grados para ángulos en medidas de radianes para los ángulos. En cada caso, primero escriba el resultado como un múltiplo fraccionario de\(\pi\) y luego use una calculadora para obtener una aproximación de 4 decimales de la medida del radián.

a)\(15^\circ\) b\(58^\circ\)) c\(112^\circ\)) d\(210^\circ\)) e\(-40^\circ\)) f\(-78^\circ\)

Ejercicio\(\PageIndex{14}\)

Convierta cada una de las siguientes mediciones de radianes para los ángulos en medidas de grado para los ángulos. Cuando sea necesario, escriba cada resultado como una aproximación de 4 decimales.

a)\(\dfrac{3}{8}\pi\) radianes b)\(\dfrac{7}{9}\pi\) radianes c)\(-\dfrac{7}{15}\pi\) radianes d)\(1\) radianes e)\(2.4\) radianes f\(3\) radianes

Contestar

(a)\(67.5^\circ\)

b)\(231. 4268^\circ\)

(d)\(57.2958^\circ\)

Ejercicio\(\PageIndex{15}\)

Dibuje un ángulo en posición estándar de un ángulo cuya medida de radianes sea:

a)\(\dfrac{1}{4}\pi\) b\(\dfrac{1}{3}\pi\)) c\(\dfrac{2}{3}\pi\)) d\(\dfrac{5}{4}\pi\)) e\(-\dfrac{1}{3}\pi\)) f\(3.4\)

Ejercicio\(\PageIndex{16}\)

En el Ejercicio 1.16, se utilizó el Applet de Geogebra llamado Puntos Terminales de Arcos en el Círculo Unitario para aproximar valores de las funciones coseno y seno. Ahora haremos algo similar para aproximar los valores de coseno y seno para ángulos medidos en grados.

Hemos visto que el lado terminal de un ángulo en posición estándar cruza el círculo unitario en un punto. Utilizamos las coordenadas de este punto para determinar el coseno y el seno de ese ángulo. Cuando el ángulo se mide en radianes, la medida radianes del ángulo es la misma que el arco en el círculo unitario subtendido por el ángulo. Esto no es cierto cuando el ángulo se mide en grados, pero aún podemos usar el punto de intersección para definir el coseno y el seno del ángulo. Entonces, si un ángulo en posición estándar tiene medición de grados\(a^\circ\), entonces\(\cos(a^\circ)\) definimos como la coordenada x del punto de intersección del lado terminal de ese ángulo y el círculo unitario. \(\sin(a^\circ)\)Definimos como la coordenada y del punto de intersección del lado terminal de ese ángulo y el círculo unitario.

Ahora utilizaremos el applet Geogebra Angles y el Unit Circle. Una dirección web para este applet es

http://gvsu.edu/s/VG

Para este applet, controlamos el valor de la entrada\(a^\circ\) con el deslizador para\(a\). Los valores de un rango de\(-180^\circ\) a\(180^\circ\) en incrementos de\(5^\circ\). Para un valor dado de\(a^\circ\), se dibuja un ángulo en posición estándar y se muestran las coordenadas del punto de intersección del lado terminal de ese ángulo y el círculo unitario. Utilice este applet para aproximar valores para cada uno de los siguientes:

a)\(\cos(10^\circ)\) y\(\sin(10^\circ)\)

b)\(\cos(60^\circ)\) y\(\sin(60^\circ)\)

c)\(\cos(135^\circ)\) y\(\sin(135^\circ)\)

d)\(\cos(-10^\circ)\) y\(\sin(-10^\circ)\)

e)\(\cos(-135^\circ)\) y\(\sin(-135^\circ)\)

f)\(\cos(85^\circ)\) y\(\sin(85^\circ)\)

Contestar

(a)\(\cos(10^\cric) \approx 0.9848, \sin(10^circ) \approx 0.1736\)

b)\(\cos(-10^\cric) \approx 0.9848, \sin(-10^circ) \approx -0.1736\)

Ejercicio\(\PageIndex{17}\)

El ejercicio (4) debe completarse antes de realizar este ejercicio. Pon la calculadora que estás usando en modo Grados. Luego usa la calculadora para determinar los valores de las funciones coseno y seno en el Ejercicio (4). ¿Los valores son los mismos? ¿En qué se diferencian?

Ejercicio\(\PageIndex{18}\)

Determine la longitud del arco (a la centésima de unidad más cercana cuando sea necesario) para cada una de las siguientes.

(a) Un arco en un círculo de radio de 6 pies que es interceptado por un ángulo central de\(\dfrac{2\pi}{3}\) radianes. Compare esto con un tercio de la circunferencia del círculo.

b) Un arco en un círculo de radio de 100 millas que es interceptado por un ángulo central de 2 radianes.

c) Un arco en un círculo de radio de 20 metros que es interceptado por un ángulo central de\(\dfrac{13\pi}{10}\) radianes radianes.

d) Un arco en un círculo de radio de 10 pies que es interceptado por un ángulo central de 152 grados.

Contestar

(a) La longitud del arco es\(4\pi\) pies, que es igual a\(\dfrac{1}{3}\) la circunferencia del círculo.

b) La longitud del arco es de\(200\) millas.

(c) La longitud del arco es de\(26\pi\) metros.

Ejercicio\(\PageIndex{19}\)

En cada una de las siguientes, cuando sea posible, determinar la medida exacta del ángulo central en radianes. De lo contrario, redondear a la centésima más cercana de un radián.

(a) El ángulo central que intercepta un arco de\(3\) pies de longitud en un círculo de\(5\) pies de radio.

(b) El ángulo central que intercepta un arco de\(18\) pies de longitud sobre un círculo de\(5\) pies de radio.

c) El ángulo central que intercepta un arco de\(20\) metros de longitud sobre un círculo de\(12\) metros de radio.

Contestar

a)\(\theta = \dfrac{3\pi}{5}\) radianes.

b)\(\theta = \dfrac{18}{5}\) radianes\(= 3.6\) radianes.

Ejercicio\(\PageIndex{20}\)

En cada una de las siguientes, cuando sea posible, determinar la medida exacta del ángulo central en grados. De lo contrario, redondear a la centésima de grado más cercana.

(a) El ángulo central que intercepta un arco de longitud 3 pies en un círculo de radio de 5 pies.

(b) El ángulo central que intercepta un arco de longitud 18 pies en un círculo de radio de 5 pies.

c) El ángulo central que intercepta un arco de longitud 20 metros sobre un círculo de radio 12 metros.

d) El ángulo central que intercepta un arco de 5 pulgadas de longitud sobre un círculo de 5 pulgadas de radio.

e) El ángulo central que intercepta un arco de 12 pulgadas de longitud sobre un círculo de 5 pulgadas de radio.

Contestar

(a)\(\theta = 108^\circ\)

b)\(\theta = (\dfrac{648}{\pi})^\circ \approx 206.26^\circ\)

Ejercicio\(\PageIndex{21}\)

Determinar la distancia (en millas) que recorre el planeta Marte en una semana a su paso alrededor del sol. Para este problema, supongamos que Marte completa una revolución completa alrededor del sol en 687 días y que el camino de Marte alrededor del sol es un círculo con un radio de 227.5 millones de millas.

Ejercicio\(\PageIndex{22}\)

Determinar la distancia (en millas) que recorre la Tierra en un día a su paso alrededor del sol. Para este problema, supongamos que la Tierra completa una revolución completa alrededor del sol en 365.25 días y que el camino de la Tierra alrededor del sol es un círculo con un radio de 92.96 millones de millas.

Ejercicio\(\PageIndex{23}\)

Un disco compacto (CD) tiene un diámetro de 12 centímetros (cm). Supongamos que el CD está en un reproductor de CD y está rotando a 225 revoluciones por minuto. ¿Cuál es la velocidad angular del CD (en radianes por segundo) y cuál es la velocidad lineal de un punto en el borde del CD?

Ejercicio\(\PageIndex{24}\)

Una persona está montando en una noria que tarda 28 segundos en hacer una revolución completa. Su asiento está a 25 pies del eje de la rueda.

a) ¿Cuál es su velocidad angular en revoluciones por minuto? ¿Radianes por minuto? ¿Grados por minuto?

b) ¿Cuál es su velocidad lineal?

c) ¿Cuál de las cantidades de velocidad angular y velocidad lineal cambian si el asiento de la persona estaba a 20 pies del eje en lugar de 25 pies? Calcular el nuevo valor para cualquier valor que cambie. Explique por qué cada valor cambia o no cambia.

Ejercicio\(\PageIndex{25}\)

Una polea pequeña con un radio de\(3\) pulgadas está conectada por una correa a una polea más grande con un radio de\(7.5\) pulgadas (Ver Figura\(\PageIndex{3}\)). La polea más pequeña está conectada a un motor que hace que gire en sentido antihorario a una velocidad de\(120\) rpm (revoluciones por minuto). Debido a que las dos poleas están conectadas por la correa, la polea más grande también gira en sentido contrario a las agujas del reloj.

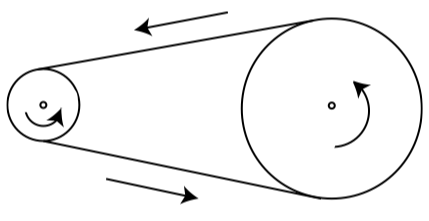
Figura\(\PageIndex{3}\): Dos poleas conectadas por una correa

(a) Determinar la velocidad angular de la polea más pequeña en radianes por minuto.

(b) Determinar la velocidad lineal de la llanta de la polea más pequeña en pulgadas por minuto.

(c) ¿Cuál es la velocidad lineal de la llanta de la polea más grande? Explique.

(d) Encontrar la velocidad angular de la polea más grande en radianes por segundo.

e) ¿Cuántas revoluciones por minuto gira la polea más grande?

Contestar

b)\(v = 720\pi\dfrac{in}{min} \approx 2261.95\dfrac{in}{min}\)

Ejercicio\(\PageIndex{26}\)

Una polea pequeña con un radio de\(10\) centímetros pulgadas está conectada por una correa a una polea más grande con un radio de\(24\) centímetros pulgadas (Ver Figura 1.16). La polea más grande está conectada a un motor que hace que gire en sentido antihorario a una velocidad de\(75\) rpm (revoluciones por minuto). Debido a que las dos poleas están conectadas por la correa, la polea más pequeña también gira en sentido contrario a las agujas del reloj.

(a) Determinar la velocidad angular de la polea más grande en radianes por minuto.

(b) Determinar la velocidad lineal de la llanta de la polea grande en pulgadas por minuto.

(c) ¿Cuál es la velocidad lineal de la llanta de la polea más pequeña? Explique.

(d) Encontrar la velocidad angular de la polea más pequeña en radianes por segundo.

e) ¿Cuántas revoluciones por minuto gira la polea más pequeña?

Contestar

b)\(v = 3600\pi\dfrac{cm}{min} \approx 11309.73\dfrac{cm}{min}\)

Ejercicio\(\PageIndex{27}\)

El radio de una rueda de automóvil es de 15 pulgadas. Si el automóvil viaja 60 millas por hora, ¿cuál es la velocidad angular de la rueda en radianes por minuto? ¿Qué tan rápido gira la rueda en revoluciones por minuto?

Ejercicio\(\PageIndex{28}\)

La distancia media de la Tierra a la Luna es de 238,857 millas. Suponiendo que la órbita de la luna alrededor de la Tierra es un círculo con un radio de 238,857 millas y que la luna hace una revolución alrededor de la Tierra cada 27.3 días, determinar la velocidad lineal de la luna en millas por hora. Investiga la distancia de la luna a la Tierra y explica por qué los cálculos que se acaban de hacer son aproximaciones

Ejercicio\(\PageIndex{29}\)

En cada uno de los siguientes se muestra un círculo unitario que muestra información sobre un arco\(t\). En cada caso, utilice la información del círculo unitario para determinar los valores de\(t\),\(\cos(t)\), y\(\sin(t)\).

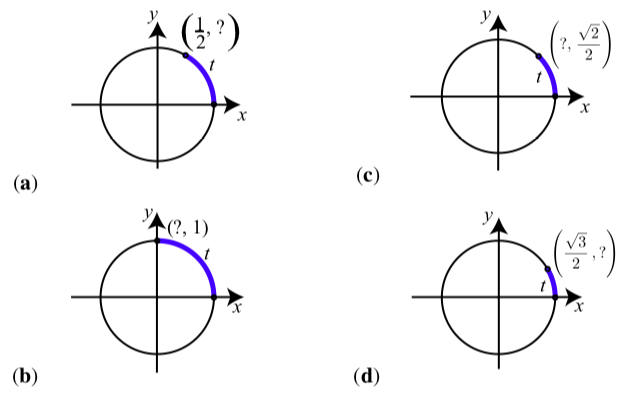
Figura\(\PageIndex{4}\)

Contestar

(a)\(t = \dfrac{\pi}{3}, \cos(t) = \dfrac{1}{2}, \sin(t) = \dfrac{\sqrt{3}}{2}\).

b)\(t = \dfrac{\pi}{2}, \cos(t) = 0, \sin(t) = 1\).

c)\(t = \dfrac{\pi}{4}, \cos(t) = \dfrac{\sqrt{2}}{2}, \sin(t) = \dfrac{\sqrt{2}}{2}\).

d)\(t = \dfrac{\pi}{6}, \cos(t) = \dfrac{\sqrt{3}}{2}, \sin(t) = \dfrac{1}{2}\).

Ejercicio\(\PageIndex{30}\)

Determine el valor exacto para cada una de las siguientes expresiones y luego use una calculadora para verificar el resultado. Por ejemplo,

\[\cos(0) + \sin(\dfrac{\pi}{3}) = 1 + \dfrac{\sqrt{3}}{2} \approx 1.8660.\]

(a)\[\cos^2(\dfrac{\pi}{6})\]

b)\[2\sin^2(\dfrac{\pi}{6}) + \cos(\pi)\]

c)\[\dfrac{\cos(\dfrac{\pi}{6})}{\sin(\dfrac{\pi}{6})}\]

(d)\[3\sin(\dfrac{\pi}{2}) + \cos(\dfrac{\pi}{4})\]

Contestar

(a)\(\cos^{2}(\dfrac{\pi}{6}) = \dfrac{3}{2}\).

b)\(2\sin^{2}(\dfrac{\pi}{4}) + \cos(\pi) = 0\).

Ejercicio\(\PageIndex{31}\)

Para cada uno de los siguientes, determine el arco de referencia para el arco dado y dibuje el arco y su arco de referencia en el círculo unitario.

(a)\(t = \dfrac{4\pi}{3}\)

b)\(t = \dfrac{13\pi}{8}\)

c)\(t = \dfrac{9\pi}{4}\)

(d)\(t = -\dfrac{4\pi}{3}\)

e\(t = -\dfrac{7\pi}{5}\)) f\(t = 5\)

Contestar

(a) El arco de referencia es\(\dfrac{\pi}{3}\).

b) El arco de referencia es\(\dfrac{3\pi}{8}\).

d) El arco de referencia es\(\dfrac{\pi}{3}\).

Ejercicio\(\PageIndex{32}\)

Para cada uno de los siguientes, dibuje el arco dado t en el círculo unitario, determine el arco de referencia para t, y luego determine los valores exactos para\(cos(t)\) y\(sin(t)\).

(a)\(t = \dfrac{5\pi}{6}\)

b)\(t = \dfrac{5\pi}{4}\)

c)\(t = \dfrac{5\pi}{3}\)

(d)\(t = -\dfrac{2\pi}{3}\)

(e)\(t = -\dfrac{7\pi}{4}\)

f)\(t = \dfrac{19\pi}{6}\)

Contestar

a) El arco de referencia es\(\dfrac{\pi}{6}\);\(\cos(\dfrac{5\pi}{6}) = -\dfrac{\sqrt{3}}{2}\);\(\sin(\dfrac{5\pi}{6}) = -\dfrac{1}{2}\).

b) El arco de referencia es\(\dfrac{\pi}{3}\);\(\cos(-\dfrac{2\pi}{3}) = -\dfrac{1}{2}\);\(\sin(-\dfrac{2\pi}{3}) = -\dfrac{\sqrt{3}}{2}\).

Ejercicio\(\PageIndex{33}\)

(a) Utilice una calculadora (en modo radianes) para determinar aproximaciones de cinco dígitos para\(\cos(4)\) y\(\sin(4)\).

(b) Utilizar una calculadora (en modo radianes) para determinar aproximaciones de cinco dígitos para\(\cos(4 - \pi)\) y\(\sin(4 - \pi)\).

c) Utilizar el concepto de arcos de referencia para explicar los resultados en las partes (a) y (b).

Ejercicio\(\PageIndex{34}\)

Supongamos que tenemos la siguiente información sobre el arco\(t\).

\[0 < t < \dfrac{\pi}{2} \space and \space sin(t) = \dfrac{1}{5}\]

Utilice esta información para determinar los valores exactos de cada uno de los siguientes:

(a)\(\cos(t)\)

b)\(\sin(\pi - t)\)

c)\(\cos(\pi - t)\)

(d)\(\sin(\pi + t)\)

(e)\(\cos(\pi + t)\)

f)\(\sin(2\pi - t)\)

Contestar

(a)\(\cos(t) = \dfrac{\sqrt{24}}{5}\).

d)\(\sin(\pi + t) = -\dfrac{1}{5}\).

Ejercicio\(\PageIndex{35}\)

Supongamos que tenemos la siguiente información sobre el arco\(t\).

\[\dfrac{\pi}{2} < t < \pi \space and \space \cos(t) = -\dfrac{2}{3}\]

Utilice esta información para determinar los valores exactos de cada uno de los siguientes:

a)\(\sin(t)\) b\(\sin(\pi - t)\)) c\(\cos(\pi - t)\)) d\(\sin(\pi + t)\)) e\(\cos(\pi + t)\)) f\(\sin(2\pi - t)\)

Ejercicio\(\PageIndex{36}\)

Asegúrate de que tu calculadora esté en Modo Radián.

(a) Utilice una calculadora para encontrar una aproximación de ocho dígitos de\(\sin(\dfrac{\pi}{6}+\dfrac{\pi}{4}) = \sin(\dfrac{5\pi}{12})\)

b) Determinar el valor exacto de\(\sin(\dfrac{\pi}{6}) + \sin(\dfrac{\pi}{4})\).

(c) Use una calculadora para encontrar una aproximación de ocho dígitos de su resultado en la parte (b). Compare esto con su resultado en la parte (a). ¿Parece que

\[\sin(\dfrac{\pi}{6}+\dfrac{\pi}{4}) = \sin(\dfrac{\pi}{6}) + sin(\dfrac{\pi}{4}).\]

d) Determinar el valor exacto de\(\sin(\dfrac{\pi}{6})\cos(\dfrac{\pi}{4}) + \cos(\dfrac{\pi}{6})\sin(\dfrac{\pi}{4})\).

(e) Determine una aproximación de ocho dígitos de su resultado en la parte (d).

f) Comparar los resultados en las partes (a) y (e). ¿Parece que

\[\sin(\dfrac{\pi}{6}+\dfrac{\pi}{4}) = \sin(\dfrac{\pi}{6})\cos(\dfrac{\pi}{4}) + \cos(\dfrac{\pi}{6})\sin(\dfrac{\pi}{4}).\]

Ejercicio\(\PageIndex{37}\)

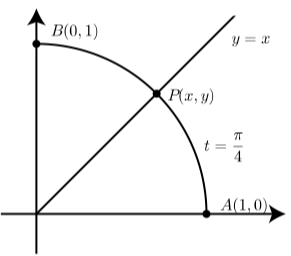
Figura\(\PageIndex{5}\)

Este ejercicio proporciona un método alternativo para determinar los valores exactos de\(\cos(\dfrac{\pi}{4})\) y\(\sin(\dfrac{\pi}{4})\). El diagrama muestra el punto terminal\(P(x, y)\) para un arco de longitud\(t = \dfrac{\pi}{4}\) en el círculo unitario. Los puntos\(A(1, 0)\) y también\(B(0, 1)\) se muestran.

Dado que el punto B es el punto terminal del arco de longitud\(\dfrac{\pi}{2}\), podemos concluir que la longitud del arco de P a B también lo es\(\dfrac{\pi}{4}\). Debido a esto, concluimos que el punto P se encuentra en la línea y D x como se muestra en el diagrama. Utilice este hecho para determinar los valores de x e y. Explique por qué esto demuestra que\[\cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2} \space and \space \sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}.\]

Ejercicio\(\PageIndex{38}\)

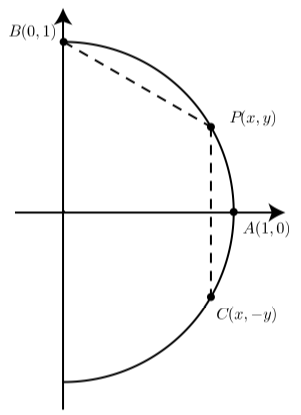
Figura\(\PageIndex{6}\)

Este ejercicio proporciona un método alternativo para determinar los valores exactos de\(\cos(\dfrac{\pi}{6})\) y\(\sin(\dfrac{\pi}{6})\). El diagrama muestra el punto terminal\(P(x, y)\) para un arco de longitud\(t = \dfrac{\pi}{6}\) en el círculo unitario. Los puntos\(A(1, 0)\),\(B(0, 1)\), y también\(C(x, -y)\) se muestran. Observe que B es el punto terminal de la Ahora\(arc \space t = -\dfrac{\pi}{6}.\)
notamos que la longitud del arco de P a B es\[\dfrac{\pi}{2} - \dfrac{\pi}{6} = \dfrac{\pi}{3}.\] Además, la longitud del arco de C a P\[\dfrac{\pi}{6} - \dfrac{-\pi}{6} = \dfrac{\pi}{3}.\]
Esto significa que la distancia de P a B es igual a la distancia de C a P.

(a) Utilice la fórmula de distancia para escribir una fórmula (en términos de x e y) para la distancia de P a B.

(b) Usar la fórmula de distancia para escribir una fórmula (en términos de x e y) para la distancia de C a P.

(c) Establecer las distancias de (a) y (b) iguales entre sí y resolver la ecuación resultante para y Para ello, comience por cuadrar ambos lados de la ecuación. Para resolver por y, puede ser necesario utilizar el hecho de que\(x^2 + y^2 = 1\).

(d) Utilizar el valor para y en (c) y el hecho de que x2 C y2 D 1 para determinar el valor para x Explique por qué esto demuestra que\[\cos(\dfrac{\pi}{6}) = \dfrac{\sqrt{3}}{2} \space and \space \sin(\dfrac{\pi}{3}) = \dfrac{1}{2}.\]

Ejercicio\(\PageIndex{39}\)

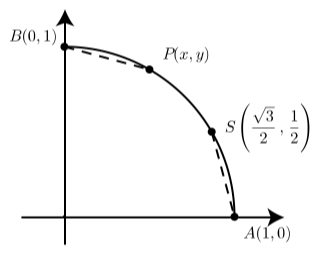
Figura\(\PageIndex{7}\)

Este ejercicio proporciona un método alternativo para determinar los valores exactos de\(\cos(\dfrac{\pi}{3})\) y\(\sin(\dfrac{\pi}{3})\). El diagrama muestra el punto terminal\(P(x, y)\) para un arco de longitud\(t = \dfrac{\pi}{3}\) en el círculo unitario. Los puntos\(A(1, 0)\),\(B(0, 1)\), y también\(S(\dfrac{\sqrt{3}}{2}, \dfrac{1}{2})\) se muestran. Observe que B es el punto terminal del\(arc \space t = \dfrac{\pi}{2}.\) Aviso de que B es el punto terminal del\(arc \space t = \dfrac{\pi}{2}.\)

A partir del Ejercicio (10), sabemos que\(S\) es el punto terminal de un arco de longitud\(\dfrac{\pi}{6}\).

Ahora notamos que la longitud del arco de\(A\) a\(P\) es\(\dfrac{\pi}{3}\). Además, dado que la longitud del arco de\(A\) a\(B\) es\(\dfrac{\pi}{2}\) y la y la longitud del arco de\(B\) a\(P\) es\(\dfrac{\pi}{3}\). Esto significa que la distancia de\(P\) a\(B\) es igual\[\dfrac{\pi}{2} - \dfrac{\pi}{3} = \dfrac{\pi}{6}.\] Dado que ambos arcos tienen longitud\(\dfrac{\pi}{6}\), la distancia de\(A\) a\(S\) es igual a la distancia de\(P\) a\(B\).

(a) Utilice la fórmula de distancia para escribir una fórmula (en términos de x e y) para la distancia de\(P\) a\(B\).

(b) Utilice la fórmula de distancia para escribir una fórmula (en términos de x e y) para la distancia de\(P\) a\(B\).

(c) Establecer las distancias de (a) y (b) iguales entre sí y resolver la ecuación resultante para\(y\). Para ello, comience por cuadrar ambos lados de la ecuación. Para resolver por y, puede ser necesario utilizar el hecho de que\(x^2 + y^2 = 1\).

d) Utilizar el valor para\(y\) en (c) y el hecho de que\(x^2 + y^2 = 1\) para determinar el valor para\(x\).

Explique por qué esto demuestra que\[\cos(\dfrac{\pi}{3}) = \dfrac{1}{2} \space and \space \sin(\dfrac{\pi}{3}) = \dfrac{\sqrt{3}}{2}.\]

Ejercicio\(\PageIndex{40}\)

Complete la siguiente tabla con los valores exactos de cada valor funcional si se define.

\(t\)	\(\cot(t)\)	\(\sec(t)\)	\(\csc(t)\)
\(0\)
\(\dfrac{\pi}{6}\)
\(\dfrac{\pi}{4}\)
\(\dfrac{\pi}{4}\)
\(\dfrac{\pi}{2}\)

Contestar

\(t\)	\(\cos(t)\)	\(\sec(t)\)	\(\csc(t)\)
\(0\)	undefined	\(1\)	undefined
\(\dfrac{\pi}{6}\)	\(\sqrt{3}\)	\(\dfrac{2}{\sqrt{3}}\)	\(2\)
\(\dfrac{\pi}{4}\)	\(1\)	\(\sqrt{2}\)	\(\sqrt{2}\)
\(\dfrac{\pi}{3}\)	\(\dfrac{1}{\sqrt{3}}\)	\(2\)	\(\dfrac{2}{\sqrt{3}}\)
\(\dfrac{\pi}{2}\)	\(0\)	undefined	\(1\)

Ejercicio\(\PageIndex{41}\)

Complete la siguiente tabla con los valores exactos de cada valor funcional si se define.

\(t\)	\(\cot(t)\)	\(\sec(t)\)	\(\csc(t)\)
\(\dfrac{2\pi}{3}\)
\(\dfrac{7\pi}{6}\)
\(\dfrac{7\pi}{4}\)
\(-\dfrac{\pi}{3}\)
\(\pi\)

Ejercicio\(\PageIndex{42}\)

Determinar el cuadrante en el que se encuentra el punto terminal de cada arco en base a la información dada.

1. \(\cos(x) > 0\)y\(\tan(x) < 0\)
2. \(\tan(x) > 0\)y\(\csc(x) < 0\)
3. \(\cot(x) > 0\)y\(\sec(x) > 0\)
4. \(\sin(x) < 0\)y\(\sec(x) > 0\)
5. \(\sec(x) < 0\)y\(\csc(x) > 0\)
6. \(\sin(x) < 0\)y\(\cot(x) > 0\)

Contestar

(a) El punto terminal se encuentra en el cuarto cuadrante.

b) El punto terminal se encuentra en el tercer cuadrante.

Ejercicio\(\PageIndex{43}\)

Si\(\sin(t) = \dfrac{1}{3}\) y\(\cos(t) < 0\), determinar los valores exactos de\(\cos(t)\),\(\tan(t)\),\(\csc(t)\),\(\sec(t)\), y\(\cot(t)\).

Contestar

1. \(\cos(t) = -\dfrac{\sqrt{8}}{3}\)
2. \(\tan(t) = -\dfrac{1}{\sqrt{8}}\)
3. \(\csc(t) = 3\)
4. \(\sec(t) = -\dfrac{3}{\sqrt{8}}\)
5. \(\cot(t) = -\sqrt{8}\)

Ejercicio\(\PageIndex{44}\)

Si\(\cos(t) = -\dfrac{3}{5}\) y\(\sin(t) < 0\), determinar los valores exactos de\(\sin(t)\),\(\tan(t)\),\(\csc(t)\),\(\sec(t)\), y\(\cot(t)\).

Ejercicio\(\PageIndex{45}\)

Si\(\sin(t) = -\dfrac{2}{5}\) y\(\tan(t) < 0\), determinar los valores exactos de\(\cos(t)\),\(\tan(t)\),\(\csc(t)\),\(\sec(t)\), y\(\cot(t)\).

Ejercicio\(\PageIndex{46}\)

Si\(\sin(t) = 0. 273\) y\(\cos(t) < 0\), determine las aproximaciones de cinco dígitos para\(\cos(t)\)\(\tan(t)\),\(\csc(t)\),\(\sec(t)\), y\(\cot(t)\).

Ejercicio\(\PageIndex{47}\)

En cada caso, determinar el arco t que satisface las condiciones dadas o explicar por qué no existe tal arco.

1. \(\tan(t) = 1, \cos(t) = -\dfrac{1}{\sqrt{2}}, and 0< t < 2\pi\)
2. \(\sin(t) = 1, \sec(t)\)no está definido, y\(0< t < \pi\)
3. \(\sin(t) = \dfrac{\sqrt{2}}{2}, \sec(t) = -\sqrt{2}, and 0< t < \pi\)
4. \(\sec(t) = -\dfrac{2}{\sqrt{3}}, \tan(t) = \sqrt{2}, and 0< t < 2\pi\)
5. \(\csc(t) = \sqrt{2}, \tan(t) = -1, and 0< t < 2\pi\)

Contestar

(a)\(t = \dfrac{5\pi}{4}\)

b)\(t = \dfrac{\pi}{2}\)

Ejercicio\(\PageIndex{48}\)

Utilice una calculadora para determinar aproximaciones decimales de cuatro dígitos para cada una de las siguientes.

1. \(\csc(1)\)
2. \(\tan(\dfrac{12\pi}{5})\)
3. \(\cot(t)\)
4. \(\sec(\dfrac{13\pi}{8})\)
5. \(\sin^2(5.5)\)
6. \(1 + \tan^2(2)\)
7. \(\sec^2(2)\)