2.3: Aplicaciones y Modelado con Funciones Sinusoidales

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

Dejar\(A, B, C\), y\(D\) ser constantes con\(B > 0\) y considerar la gráfica de\(f(t) = A\sin(B(t - C)) + D\) o\(f(t) = A\cos(B(t - C)) + D\).

• ¿Qué significa frequency?
• ¿Cómo modelizamos los datos periódicos con precisión con una función sinusoidal?
• ¿Qué es un modelo matemático?
• ¿Por qué es razonable utilizar una función sinusoidal para modelar fenómenos periódicos?

En la Sección 2.2, utilizamos el diagrama de la Figura\(\PageIndex{1}\) para ayudar a recordar hechos importantes sobre las funciones sinusoidales.

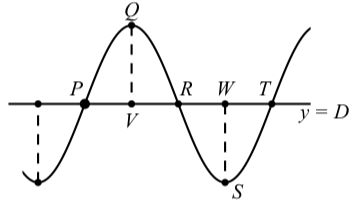
Figura\(\PageIndex{1}\): Gráfica de una sinusoide

Por ejemplo:

• La distancia horizontal entre un punto donde ocurre un máximo y el siguiente punto donde ocurre un mínimo (como puntos\(Q\) y\(S\)) es la mitad de un período. Esta es la longitud del segmento desde\(V\) hasta\(W\) en la Figura\(\PageIndex{1}\).
• La distancia vertical entre un punto donde ocurre un mínimo (como un punto\(S\)) y un punto donde se produce el máximo (como punto\(Q\)) es igual a dos veces la amplitud.
• La línea central\(y = D\) para la sinusoide está a medio camino entre el valor máximo en el punto\(Q\) y el valor mínimo en el punto\(S\). El valor de se\(D\) puede encontrar calculando el promedio\(y\) de las coordenadas de estos dos puntos.
• La distancia horizontal entre dos puntos sucesivos cualesquiera en la línea\(y = D\) de la Figura\(\PageIndex{1}\) es de un cuarto de período.

En Progress Check 2.16, utilizaremos algunos de estos hechos para ayudar a determinar una ecuación que modelará el volumen de sangre en el corazón de una persona en función del tiempo. Un modelo matemático es una función que describe algún fenómeno. Para los objetos que presentan un comportamiento periódico, se puede utilizar una función sinusoidal como modelo ya que estas funciones son periódicas. Sin embargo, el concepto de frecuencia se utiliza en algunas aplicaciones de fenómenos periódicos en lugar del periodo.

Definición

La frecuencia de una función sinusoidal es el número de periodos (o ciclos) por unidad de tiempo.

Una unidad típica para la frecuencia es el hertz. Un hercio (Hz) es un ciclo por segundo. Esta unidad lleva el nombre de Heinrich Hertz (1857 — 1894).

Dado que la frecuencia es el número de ciclos por unidad de tiempo, y el periodo es la cantidad de tiempo para completar un ciclo, vemos que la frecuencia y el período están relacionados de la siguiente manera:

\[frequency = \dfrac{1}{period}.\]

Ejercicio\(\PageIndex{1}\)

El volumen del corazón promedio es de 140 mililitros (ml), y empuja aproximadamente la mitad de su volumen (70 ml) con cada latido. Además, la frecuencia del latido del corazón para un atleta bien entrenado para un atleta bien entrenado es de 50 latidos (ciclos) por minuto. Modelaremos el volumen, V.t/(en mililitros) de sangre en el corazón en función del tiempo t medido en segundos. Usaremos una función sinusoidal de la forma\[V(t) = A\cos(B(t - C)) + D\]

Si elegimos tiempo 0 minutos para que sea un momento en el que el volumen de sangre en el corazón sea el máximo (el corazón está lleno de sangre), entonces es razonable usar una función coseno para nuestro modelo ya que la función coseno alcanza un valor máximo cuando su entrada es 0 y así podemos usar\(C = 0\), que corresponde a una fase turno de 0. Entonces nuestra función se puede escribir como\(V(t) = A\cos(Bt) + D\).

1. ¿Cuál es el valor máximo de\(V(t)\)? ¿Cuál es el valor mínimo de\(V(t)\)? Utilizar estos valores para determinar los valores de\(A\) y\(D\) para nuestro modelo? Explique.
2. Dado que la frecuencia de los latidos cardíacos es de 50 latidos por minuto, sabemos que el tiempo para un latido del corazón será de 1 de minuto. Determine el tiempo (en 50 segundos) que tarda en completar un latido del corazón (ciclo). Este es el periodo para esta función sinusoidal. Utilice este periodo para determinar el valor de B. Escriba la fórmula para\(V(t)\) usar los valores de\(A, B, C\), y\(D\) que se hayan determinado.

Contestar

El valor máximo de\(V(t)\) es\(140\) ml y el valor mínimo de\(V(t)\) es\(70\) ml. Entonces la diferencia\((140 - 70 = 70)\) es el doble de la amplitud. De ahí que la amplitud sea\(35\) y vamos a utilizar\(A = 35\). La línea central será entonces\(35\) unidades por debajo del máximo. Es decir,\(D = 140 - 35 = 105\).

Ya que hay\(50\) latidos por minuto, el periodo es\(\dfrac{1}{50}\) de un minuto. Ya que estamos usando segundos para el tiempo, el periodo es\(\dfrac{60}{50}\) segundos o\(\dfrac{6}{5}\) seg. Podemos determinar\(B\) resolviendo la ecuación\[\dfrac{2\pi}{B} = \dfrac{6}{5}\] para\(B\). Esto da\(B = \dfrac{10\pi}{6} = \dfrac{5\pi}{3}\). Nuestra función es

\[V(t) = 35\cos(\dfrac{5\pi}{3}t) + 105.\]

Ejemplo\(\PageIndex{1}\):

(Continuación de Comprobación de Progreso 2.16)

Ahora que hemos determinado que\[V(t) = 35\cos(\dfrac{5\pi}{3}t) + 105\]

(donde\(t\) se mide en segundos ya que el corazón estaba lleno y\(V(t)\) se mide en mililitros) es un modelo para la cantidad de sangre en el corazón, podemos utilizar este modelo para determinar otros valores asociados a la cantidad de sangre en el corazón. Por ejemplo:

Podemos determinar la cantidad de sangre en el corazón\(1\) segundo después de que el corazón se llenó usando\(t = 1\). \[V(1) = 35\cos(\dfrac{5\pi}{3}) + 105\]Entonces podemos decir que\(1\) segundo después de que el corazón esté lleno, habrá\(122.5\) mililitros de sangre en el corazón.

De manera similar,\(4\) segundos después de que el corazón esté lleno de sangre, habrá\(87.5\) mililitros de sangre en el corazón ya que\[V(4) = 35\cos(\dfrac{20\pi}{3}) + 105 \approx 87.5\]

Supongamos que queremos saber en qué momentos después de que el corazón esté lleno que habrá 100 mililitros de sangre en el corazón. Podemos determinar esto si podemos resolver la ecuación\(V(t) = 100\) para\(t\). Es decir, tenemos que resolver la ecuación\[35\cos(\dfrac{5\pi}{3}t) + 105 = 100\]

Aunque aprenderemos otros métodos para resolver este tipo de ecuaciones más adelante en el libro, podemos usar una utilidad gráfica para determinar soluciones aproximadas para esta ecuación. La figura\(\PageIndex{2}\) muestra las gráficas de\(y = V(t)\) y\(y = 100\). Para resolver la ecuación, necesitamos usar una utilidad gráfica que nos permita determinar o aproximar los puntos de intersección de dos gráficas. (Esto se puede hacer usando la mayoría de las calculadoras de Texas Instruments y Geogebra.) La idea es encontrar las coordenadas de los puntos\(P, Q\), y\(R\) en la Figura\(\PageIndex{2}\).

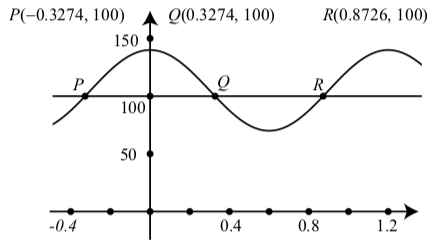
Figura\(\PageIndex{2}\): Gráfica de\(V(t) = 35\cos(\dfrac{5\pi}{3}) + 105\) y\(y = 100\)

Realmente solo necesitamos encontrar las coordenadas de uno de esos puntos ya que podemos usar propiedades de sinusoides para encontrar los demás. Por ejemplo, podemos determinar que las coordenadas de\(P\) son\((-0.3274, 100)\). Entonces usando el hecho de que la gráfica de\(y = V(t)\) es simétrica alrededor del eje y, sabemos que las coordenadas de\(Q\) son\((0.3274, 100)\). Entonces podemos usar la propiedad periódica de la función, para determinar la\(t\) coordenada de\(R\) sumando un punto a la\(t\) coordenada de\(P\). Esto da\(0.3274 + \dfrac{6}{5} = 0.8726\), y las coordenadas de\(R\) son\((0.8726, 100)\). También podemos usar la propiedad periódica para determinar tantas soluciones de la ecuación\(V(t) = 100\) como queramos.

Ejercicio\(\PageIndex{2}\)

El solsticio de verano en 2014 fue el 21 de junio y el solsticio de invierno fue el 21 de diciembre. Las horas máximas de luz diurna se dan en el solsticio de verano y las horas mínimas de luz se dan en el solsticio de invierno. Según el sitio web del Observatorio Naval de Estados Unidos, AA.usno.navy.mil/data/docs/dur_oneyear.php,

el número de horas de luz diurna en Grand Rapids, Michigan el 21 de junio de 2014 fue de 15.35 horas, y el número de horas de luz del día del 21 de diciembre de 2014 fue de 9.02 horas. Esto significa que en Grand Rapids,

• El número máximo de horas de luz diurna fue\(15.35\) horas y ocurrió el día\(172\) del año.
• El número mínimo de horas de luz diurna fue\(9.02\) horas y ocurrió el día\(355\) del año.

1. Deja\(y\) ser el número de horas de luz del día en 2014 en Grand Rapids y deja que\(t\) sea el día del año. Determinar un modelo sinusoidal para el número de horas de luz diurna\(y\) en 2014 en Grand Rapids en función de\(t\).

2. Según este modelo,

• a) ¿Cuántas horas de luz había el 10 de marzo de 2014?
• b) ¿En qué días del año había 13 horas de luz diurna?

Contestar

1. Como tenemos las coordenadas para un punto alto y bajo, primero hacemos los siguientes cálculos:

\(2(amp) = 15.35 - 9.02 = 6.33\). De ahí que la amplitud sea\(3.165\).

\[D = 9.02 + 3.165 = 12.185\].

\(\dfrac{1}{2}\)periodo\(= 355 - 172 = 183\). Entonces el periodo es\(366\). Tenga en cuenta que solemos decir que hay\(365\) días en un año. Por lo que también sería razonable utilizar un periodo de\(365\) días. Usando un periodo de\(366\) días, encontramos que\[\dfrac{2\pi}{B} = 366\]

y por lo tanto\(B = \dfrac{\pi}{183}\).

Ahora debemos decidir si usar una función sinusoidal o una función coseno para obtener el desplazamiento de fase. Ya que tenemos las coordenadas de un punto alto, usaremos una función coseno. Para ello, el desplazamiento de fase será de 172. Entonces nuestra función es

\[y = 3.165\cos(\dfrac{\pi}{183}(t - 172)) + 12.185\]

Podemos verificar esto verificando que cuando\(t = 155, y = 15.135\) y que cuando\(t = 355, y = 9.02\).

(a) Marzo\(10\) es día número\(69\). Así que usamos\(t = 69\) y obtenemos\[y = 3.165\cos(\dfrac{\pi}{183}(69 - 172)) + 12.185 \approx 11.5642\]

Por lo que el 10 de marzo de 2014, había alrededor de\(11.564\) horas de luz diurna.

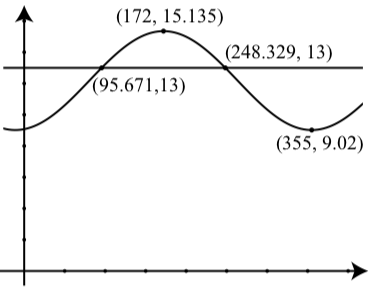
(b) Utilizamos una utilidad gráfica para aproximar los puntos de intersección de\(y = 3.165\cos(\dfrac{\pi}{183}(69 - 172)) + 12.125\) y\(y = 13\). Los resultados se muestran a la derecha. Por lo que el día 96 (6 de abril de 2014) y el día 248 (5 de septiembre), hubo alrededor de 13 horas de luz diurna.

Determinación de una sinusoide a partir de datos

En Progreso Verifique 2.18 los valores y tiempos para las horas máximas y mínimas de luz diurna. Aunque sepamos que algún fenómeno es periódico, es posible que no conozcamos los valores del máximo y mínimo. Por ejemplo, en la siguiente tabla se muestra el número de horas de luz diurna (redondeadas a la centésima de hora más cercana) el primero del mes para Edimburgo, Escocia\((55^\circ 57' N, 3^\circ 12' W)\).

Utilizaremos una función sinusoidal de la forma\(y = A\sin(B(t - C)) + D\), donde\(y\) está el número de horas de luz diurna y\(t\) es el tiempo medido en meses para modelar estos datos. Utilizaremos el 1 de enero, el 2 de febrero, etc. como primer intento, lo usaremos\(17.48\) para las horas máximas de luz diurna y\(7.08\) para las horas mínimas de luz diurna.

Ene	Feb	Mar	Abr	Mayo	junio	julio	Ago	Sept	Oct	Nov	Dic
7.08	8.60	10.73	13.15	15.40	17.22	17.48	16.03	13.82	11.52	9.18	7.40

Tabla 2.2: Horario de luz en Edimburgo

• Ya que\(17.48 - 7.08 = 10.4\), vemos que la amplitud es 5.2 y así\(A = 5.2\).
• El desplazamiento vertical será\(7.08 + 5.2 = 12.28\) y así\(D = 12.28\).
• El periodo es de 12 meses y así\(B = \dfrac{2\pi}{12} = \dfrac{\pi}{6}\).
• El máximo ocurre en\(t = 7\). Para una función sinusoidal, el máximo es de un cuarto de período desde el momento en que la función sinusoidal cruza su eje horizontal. Esto indica un desplazamiento de fase de 4 a la derecha. Entonces\(C = 4\).

Entonces usaremos la función\(y = 5.2\sin(\dfrac{\pi}{6}(t - 4)) + 12.28\) para modelar el número de horas de luz diurna. La figura\(\PageIndex{3}\) muestra una gráfica de dispersión para los datos y una gráfica de esta función. Aunque la gráfica se ajusta razonablemente bien a los datos, parece que deberíamos poder encontrar un mejor modelo. Uno de los problemas es que el número máximo de horas de luz diurna no ocurre el 1 de julio. Probablemente ocurre unos 10 días antes. El mínimo tampoco ocurre el 1 de enero y probablemente sea algo menor que 7.08 horas. Por lo que intentaremos un máximo de 17.50 horas y un mínimo de 7.06 horas. Además, en lugar de que el máximo ocurra en\(t = 7\), diremos que ocurre a t D 6:7. Usando estos valores, tenemos\(A = 5.22, B = \dfrac{\pi}{6}, C = 3.7, \space and \space D = 12.28\). La Figura 2.22 muestra una gráfica de dispersión de los datos y una gráfica de\[y = 5.22\sin(\dfrac{\pi}{6}(t - 3.7)) + 12.28\]

Esto parece modelar muy bien los datos. Una cosa importante a tener en cuenta es que al tratar de determinar una sinusoide que “se ajuste” o modele datos reales, no hay una sola respuesta correcta. A menudo tenemos que encontrar un modelo y luego usar nuestro juicio para determinar un mejor modelo. Hay una ecuación matemática de “mejor ajuste” para una sinusoide que se llama la ecuación de regresión sinusoidal. Tenga en cuenta que necesitamos usar alguna utilidad gráfica o software para obtener una ecuación de regresión sinusoidal. Muchas calculadoras de Texas Instruments tienen tal característica como lo hace el software Geogebra. A continuación se presenta una ecuación de regresión sinusoidal para el número de horas de luz diurna en Edimburgo que se muestra en la Tabla 2.2 obtenida de Geogebra.

\[y = 5.153\sin(0.511t - 1.829) + 12.174\]

En la Figura se muestra una gráfica de dispersión con una gráfica de esta función\(\PageIndex{5}\).

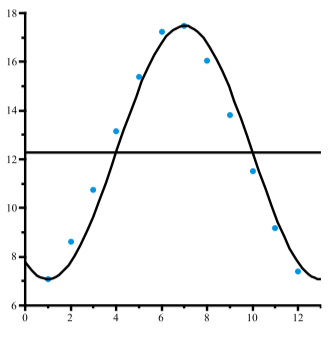
Figura\(\PageIndex{3}\): Horario de luz en Edimburgo

Nota

Consulte los suplementos al final de esta sección para obtener instrucciones sobre cómo usar Geogebra y un TI-84 de Texas Instruments para determinar una ecuación de regresión sinusoidal para un conjunto determinado de datos.

Es interesante comparar la ecuación (1) y la ecuación (2), las cuales son modelos para los datos del Cuadro 2.2. Podemos ver que ambas ecuaciones tienen una amplitud similar y un desplazamiento vertical similar, pero notemos que la ecuación (2) no está en nuestra forma estándar para la ecuación de una sinusoide. Por lo que no podemos decir de inmediato qué dice esa ecuación sobre el periodo y el cambio de fase. En esta siguiente actividad, aprenderemos a determinar el periodo y desplazamiento de fase para sinusoides cuyas ecuaciones son de la forma\(y = a\sin(bt + c) + d\) o\(y = a\cos(bt + c) + d\).

Actividad 2.19 (Trabajar con sinusoides que no están en forma estándar)

Hasta el momento, hemos estado trabajando con sinusoides cuyas ecuaciones son de la forma\(y = A\sin(B(t - C)) + D\) o\(y = A\cos(B(t - C)) + D\). Cuando se escribe en esta forma, podemos usar los valores de\(A, B, C\), y\(D\) para determinar la amplitud,

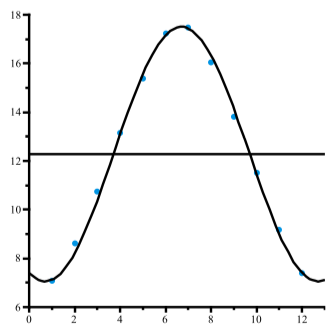
Figura\(\PageIndex{4}\): Horario de luz en Edimburgo

período, desplazamiento de fase y desplazamiento vertical de la sinusoide. Siempre debemos recordar, sin embargo, que para ello, la ecuación debe escribirse exactamente en esta forma. Si tenemos una ecuación en una forma ligeramente diferente, tenemos que determinar si hay alguna manera de usar álgebra para reescribir la ecuación en la forma\(y = A\sin(B(t - C)) + D\) o\(y = A\cos(B(t - C)) + D\). Considera la ecuación\(y = 2\sin(3t + \dfrac{\pi}{2})\)

• Utilice una utilidad gráfica para dibujar la gráfica de esta ecuación con\(-\dfrac{\pi}{3} \leq t \leq \dfrac{2\pi}{3} \) y. ¿Esta parece ser la gráfica de una sinusoide? Si es así, ¿puede usar la gráfica para encontrar su amplitud, período, desplazamiento de fase y desplazamiento vertical?
• Es posible verificar cualquier observación que se hiciera usando un poco de álgebra para escribir esta ecuación en la forma\(y = A\sin(B(t - C)) + D\). La idea es reescribir el argumento de la función seno, que es\(3t + \dfrac{\pi}{2}\) por “factorizar un 3” a partir de ambos términos. Esto puede parecer un poco extraño ya que no estamos acostumbrados a usar fracciones cuando factorizamos. Por ejemplo, es bastante fácil factorizar\(3y + 12\) como\[3y + 12 = 3(y + 4)\]
• Con el fin de “factor” tres de\(\dfrac{\pi}{2}\), básicamente utilizamos el hecho de que\(3 \cdot \dfrac{1}{3} = 1\)

  

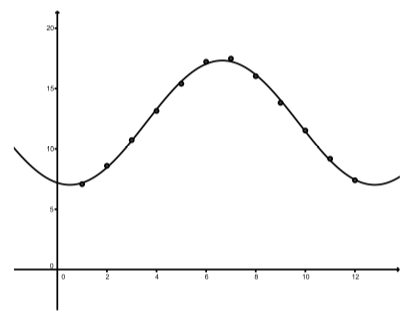
  Figura\(\PageIndex{5}\): Horario de luz en Edimburgo

  Así podemos escribir\[\dfrac{\pi}{2} = 3 \cdot \dfrac{1}{3} \cdot \dfrac{\pi}{6} = 3 \cdot \dfrac{\pi}{6}\]

  Ahora reescribe\(3t + \dfrac{\pi}{2}\) factorizando un 3 y luego reescribe\(y = 2\sin(3t + \dfrac{\pi}{2})\) en el formulario\(y = A\sin(B(t - C)) + D\).

  3. ¿Para qué sirve la amplitud, el período, el desplazamiento de fase y el desplazamiento vertical\(y = 2\sin(3t + \dfrac{\pi}{2})\)?

  En la Actividad 2.19, hicimos un poco de factorización para demostrar que\[y = 2\sin(3t + \dfrac{\pi}{2}) = 2\sin(3(t + \dfrac{\pi}{6}))\]\[y = 2\sin(3(t - (-\dfrac{\pi}{6})))\]

  Entonces podemos ver que tenemos una función sinusoidal y que la amplitud es 3, el periodo es 2, el desplazamiento de fase es\(\dfrac{2\pi}{3}\), y el desplazamiento vertical es 0.
  En general, podemos ver que si\(b\) y\(c\) son números reales, entonces\[bt + c = b(t + \dfrac{c}{b}) = b(t - (-\dfrac{c}{d}))\]

  Esto significa que\[y = a\sin(bt + c) + d = a\sin(b(t - (-\dfrac{c}{d}))) + d\]

  Entonces tenemos el siguiente resultado:

  Si\(y = a\sin(bt + c) + d\) o\(y = a\cos(bt + c) + d\), entonces

• La amplitud de la sinusoide es\(|a|\).
• El periodo de la sinusoide es\(\dfrac{2\pi}{b}\)
• El desplazamiento de fase de la sinusoide es\(-\dfrac{c}{b}\)
• El desplazamiento vertical de la sinusoide es\(d\).

Ejercicio\(\PageIndex{3}\)

• Determinar la amplitud, periodo, desplazamiento de fase y desplazamiento vertical para cada una de las siguientes sinusoides. Luego usa esta información para graficar un periodo completo de la sinusoide y establecer las coordenadas de un punto alto, un punto bajo y un punto donde la sinusoide cruza la línea central.

  (a)\(y = -2.5\cos(3x + \dfrac{\pi}{3}) + 2\)

  b)\(y = 4\sin(100\pi x - \dfrac{\pi}{4})\)

• Determinamos dos modelos sinusoidales para el número de horas de luz diurna en Edimburgo, Escocia que se muestran en la Tabla 2.2. Estos fueron

  \[y = 5.22\sin(\dfrac{\pi}{6}(t - 3.7)) + 12.28\]\[y = 5.153\sin(0.511t - 1.829) + 12.174\]

• La segunda ecuación se determinó usando una característica de regresión sinusoidal en una utilidad gráfica. Compare las amplitudes, periodos, desplazamientos de fase y desplazamientos verticales de estas dos funciones sinusoidales.

Contestar

1. (a) La amplitud es\(2.5\).

El periodo es\(\dfrac{2\pi}{3}\).

El desplazamiento de fase es\(-\dfrac{\pi}{9}\). El desplazamiento vertical es\(2\).

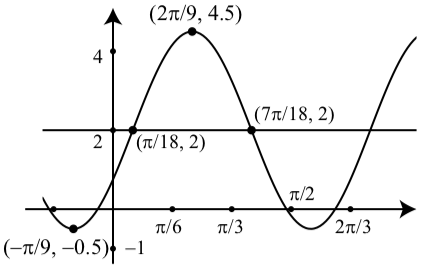
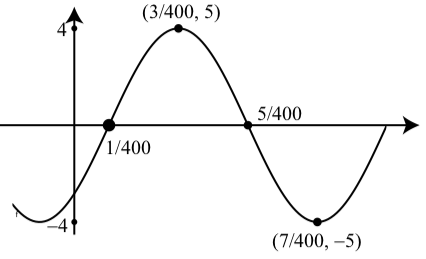
(b) La amplitud es\(4\).

El periodo es\(\dfrac{1}{50}\)

El desplazamiento de fase es\(\dfrac{1}{400}\).

El desplazamiento vertical es\(0\).

primera ecuación		segunda ecuación
\(5.22\)	amplitud	\(5.153\)
\(12\)	periodo	\(12.30\)
\(3.7\)	desplazamiento de fase	\(3.58\)
\(12.28\)	desplazamiento vertical	\(12.174\)

Suplemento — Regresión sinusoidal usando Geogebra

Antes de dar instrucciones escritas para crear una ecuación de regresión sinusoidal en Geogebra, cabe señalar que hay una Playlist de Geogebra en el Canal de Matemáticas de la Universidad Estatal de Grand Valley en YouTube. La dirección web es http://gvsu.edu/s/QA

Los cast de pantallas de video que son de mayor interés por ahora son:

• Geogebra—Basicgraphing
• GeoGebra: copia de la vista de gráficos
• Geogebra — Puntos de trazado
• Geogebra — Regresión sinusoidal

Para ilustrar el procedimiento para una ecuación de regresión sinusoidal usando Geogebra, utilizaremos los datos del Cuadro 2.2 en la página 115.

Paso 1. Establecer una ventana de visualización que sea apropiada para los datos que se van a utilizar.

Paso 2. Ingresa los puntos de datos. Hay tres formas de hacerlo.

• Quizás la forma más eficiente de ingresar puntos es usar la vista de hoja de cálculo. Para ello, haga clic en el Menú Ver y seleccione Hoja de Cálculo. A la derecha se abrirá una pequeña hoja de cálculo. Aunque puede usar cualquier conjunto de filas y columnas, una manera fácil es usar las celdas A1 y B1 para el primer punto de datos, las celdas A2 y B2 para el segundo punto de datos, y así sucesivamente. Entonces las primeras filas de la hoja de cálculo serían:

  	\(A\)	\(B\)
  1	\ (A\) ">1	\ (B\) ">7.08
  2	\ (A\) ">2	\ (B\) ">8.6
  3	\ (A\) ">3	\ (B\) ">10.73

Una vez ingresados todos los datos, para trazar los puntos, seleccione las filas y columnas en la hoja de cálculo que contengan los datos, luego haga clic en la pequeña flecha hacia abajo en la parte inferior derecha del botón con la etiqueta\({1, 2}\) y seleccione “Crear Lista de Puntos”. Aparecerá una pequeña pantalla emergente en la que se puede dar nombre a la lista de puntos. El nombre predeterminado es “list'” pero eso se puede cambiar si se desea. Ahora haga clic en el botón Crear en la parte inferior derecha de la pantalla emergente. Si se ha establecido una ventana de visualización adecuada, los puntos deben aparecer en la vista gráfica. Por último, cierre la vista de hoja de cálculo.

• Ingresa cada punto por separado como un par de pedidos. Por ejemplo, para el primer punto de la Tabla 2.2, entraríamos\((1, 7.08)\). En este caso, a cada punto se le dará un nombre como\(A, B, C\), etc.
• Ingresa todos los puntos en una lista. Por ejemplo (para un conjunto más pequeño de puntos), podríamos ingresar algo así como\ [pts = {(-3, 3), (-2, -1), (0, 1), (1, 3), (3, 0)}\) Observe que la lista de pares ordenados debe estar encerrada entre llaves.

Paso 3. Utilice el comando FitSin. La forma en que se utilice esto depende de qué opción se utilizó para ingresar y trazar los puntos de datos.

• Si se ha creado una lista de puntos (como una lista con nombre 1), simplemente ingrese\[f(x) = FitSin[list1]\] Todo lo que se necesita es el nombre de la lista dentro de los corchetes.
• Si se han ingresado puntos de datos separados, incluya los nombres de todos los puntos dentro de los corchetes y sepárelos con comas. Una versión abreviada de esto es\ [f (x) = FitSin [A, B, C]\) La ecuación de regresión sinusoidal se mostrará ahora en la vista Álgebra y se graficará en la vista gráfica.

Paso 4. Seleccione la opción de redondeo que se va a utilizar. (Este paso podría realizarse en cualquier momento). Para ello, da clic en el menú Opciones y selecciona Redondeo.

Resumen

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

• La frecuencia de una función sinusoidal es el número de periodos (o ciclos) por unidad de tiempo. \[frequency = \dfrac{1}{period}\]
• Un modelo matemático es una función que describe algún fenómeno. Para los objetos que presentan un comportamiento periódico, se puede utilizar una función sinusoidal como modelo ya que estas funciones son periódicas.

Para determinar una función sinusoidal que modele un fenómeno periódico, necesitamos determinar la amplitud, el período y el desplazamiento vertical para los fenómenos periódicos. Además, necesitamos determinar si se debe utilizar una función coseno o una función sinusoidal y el desplazamiento de fase resultante.Se puede determinar una ecuación de regresión sinusoidal que sea un “mejor ajuste” matemático para los datos de un fenómeno periódico.