2.4: Gráficas de las Otras Funciones Trigonométricas

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Cuáles son las propiedades importantes de la gráfica de\(y = \tan(t)\). Es decir, ¿cuál es el dominio y cuál es el rango de la función tangente, y qué sucede con los valores de la función tangente en los puntos que están cerca de puntos no en el dominio de la función tangente?
• ¿Cuáles son las propiedades importantes de la gráfica de\(y = \sec(t)\). Es decir, ¿cuál es el dominio y cuál es el rango de la función secante, y qué sucede con los valores de la función secante en los puntos que están cerca de puntos no en el dominio de la función secante?
• ¿Cuáles son las propiedades importantes de la gráfica de\(y = \cot(t)\). Es decir, ¿cuál es el dominio y cuál es el rango de la función cotangente, y qué sucede con los valores de la función cotangente en los puntos que están cerca de puntos no en el dominio de la función cotangente?
• ¿Cuáles son las propiedades importantes de la gráfica de\(y = \csc(t)\). Es decir, ¿cuál es el dominio y cuál es el rango de la función cosecante, y qué sucede con los valores de la función cosecante en los puntos que están cerca de puntos no en el dominio de la función cosecante?

Hemos visto como las gráficas de las funciones coseno y seno están determinadas por la definición de estas funciones. También se investigaron los efectos de las constantes\(A, B, C\), y\(D\) sobre la gráfica\(y = A\sin(B(x - C)) + D\) y la gráfica de\(y = A\sin(B(x - C)) + D\).

En la siguiente actividad inicial, exploraremos la gráfica de la función tangente. Más adelante en esta sección, discutiremos la gráfica de la función secante, y en los ejercicios se explorarán las gráficas de las funciones cotangente y cosecante. Una de las características clave de estas gráficas es el hecho de que todas tienen asíntotas verticales. Al final de esta sección se resume información importante sobre las cuatro funciones.

Actividad inicial

1. Utilice una utilidad gráfica para dibujar la gráfica de\(f(x) = \dfrac{1}{(x+1)(x-1)}\) usar\(-2 \leq x \leq 2\) y\(-10 \leq y \leq 10\). Si es posible, utilice la utilidad gráfica para dibujar las gráficas de las líneas verticales\(x = -1\) y\(x = 1\). La gráfica de la función\(f\) tiene asíntotas verticales\(x = -1\) y\(x = 1\). La razón de esto es que a estos valores de\(x\), el numerador de la función no es cero y el denominador es 0. Entonces\(x = -1\) y no\(x = 1\) están en el dominio de esta función. En general, si una función es un cociente de dos funciones, entonces habrá una asíntota vertical para aquellos valores de x para los que el numerador no es cero y el denominador es cero. Veremos esto para las funciones tangente, cotangente, secante y cosecante.
2. ¿Cómo se define la función tangente? Complete lo siguiente: Por cada número real\(x\) con\(\cos(t) \neq 0, \tan(t) = ?\).
3. Utilice una utilidad gráfica para dibujar la gráfica de\(y = \tan(t)\) usar\(-\pi \leq t \leq \pi\) y\(-10 \leq y \leq 10\).
4. ¿Cuáles son algunas de las asíntotas verticales de la gráfica de la función\(y = \tan(t)\)? ¿Cuál parece ser el rango de la función tangente?

La Gráfica de la Función Tangente

La gráfica de la función tangente es muy diferente a las gráficas de las funciones seno y coseno. Una razón es que porque\(\tan(t) = \dfrac{\sin(t)}{\cos(t)}\), hay valores de\(t\) para los cuales no\(\tan(t)\) está definido. Hemos visto que el dominio de la función tangente es el conjunto de todos los números reales\(t\) para los cuales\(t = \neq \dfrac{\pi}{2} + k\pi\) para cada entero\(k\).

En particular, los números reales\(\dfrac{\pi}{2}\) y no\(-\dfrac{\pi}{2}\) están en el dominio de la función tangente. Entonces la gráfica de la función tangente tendrá asíntotas verticales en\(t = \dfrac{\pi}{2}\) y\(t = -\dfrac{\pi}{2}\) (así como en otros valores). Deberíamos haber observado esto en la actividad inicial.

Entonces, para dibujar una gráfica precisa de la función tangente, será necesario entender el comportamiento de la tangente cerca de los puntos que no están en su dominio. Ahora investigamos el comportamiento de la tangente para puntos cuyos valores de\(t\) eso son ligeramente menores que\(\dfrac{\pi}{2}\) y para puntos cuyos valores de t que son ligeramente mayores que\(-\dfrac{\pi}{2}\). Usando una calculadora, podemos obtener los valores que se muestran en la Tabla 2.4.

\(t\)	\(\tan(t)\)
\ (t\) ">\(\dfrac{\pi}{2} - 0.1\)	\ (\ tan (t)\) ">9.966644423
\ (t\) ">\(\dfrac{\pi}{2} - 0.01\)	\ (\ tan (t)\) ">99.99666664
\ (t\) ">\(\dfrac{\pi}{2} - 0.001\)	\ (\ tan (t)\) ">999.9996667
\ (t\) ">\(\dfrac{\pi}{2} - 0.0001\)	\ (\ tan (t)\) ">9999.999967
\ (t\) ">\(\dfrac{\pi}{2} + 0.1\)	\ (\ tan (t)\) ">-9.966644423
\ (t\) ">\(\dfrac{\pi}{2} + 0.01\)	\ (\ tan (t)\) ">-99.99666664
\ (t\) ">\(\dfrac{\pi}{2} + 0.001\)	\ (\ tan (t)\) ">-999.9996667
\ (t\) ">\(\dfrac{\pi}{2} + 0.0001\)	\ (\ tan (t)\) ">-9999.999967

Cuadro 2.4: Tabla de Valores para la Función Tangente

Entonces, a medida que la entrada\(t\) se acerca\(\dfrac{\pi}{2}\) pero permanece menor que\(\dfrac{\pi}{2}\), los valores de\(\tan(t)\) son cada vez más grandes, aparentemente sin límite. Del mismo modo, la entrada\(t\) se acerca\(-\dfrac{\pi}{2}\) pero permanece mayor que\(-\dfrac{\pi}{2}\), los valores de tan.t/se están alejando cada vez más de 0 en la dirección negativa, aparentemente sin límite. Esto lo podemos ver en la definición de la tangente: como\(t\) se acerca\(\dfrac{\pi}{2}\) desde la izquierda,\(\cos(t)\) se acerca a 0 y\(\sin(t)\) se acerca a 1. Ahora\(\tan(t) = \dfrac{\sin(t)}{\cos(t)}\) y fracciones donde el numerador está cerca\(1\) y el denominador cercano para\(0\) tener valores muy grandes. Del mismo modo, a medida que t se acerca\(-\dfrac{\pi}{2}\) desde la derecha,\(\cos(t)\) se acerca a\(0\) (pero es negativo) y\(\sin(t)\) se acerca a\(1\). Las fracciones donde el numerador está cerca de 1 y el denominador cercano a 0, pero negativo, son números negativos muy grandes (en magnitud).

Ejercicio\(\PageIndex{1}\)

1. Utilice una utilidad gráfica para dibujar la gráfica de\(y = \tan(t)\) usar\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\) y\(-10 \leq y \leq 10\).
2. Utilice una utilidad gráfica para dibujar la gráfica de\(y = \tan(t)\) usar\(-\dfrac{3\pi}{2} \leq t \leq \dfrac{3\pi}{2}\) y\(-10 \leq y \leq 10\).
3. ¿Estas gráficas son consistentes con la información que hemos discutido sobre las asíntotas verticales para la función tangente?
4. ¿Cuál parece ser el rango de la función tangente?
5. ¿Cuál parece ser el periodo de la función tangente?

Contestar

A continuación se muestran las gráficas para (1) y (2).

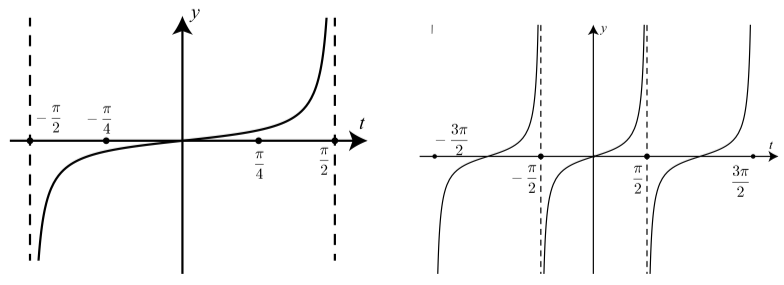
En ambas gráficas, la gráfica justo a la izquierda\(t = \dfrac{\pi}{2}\) y justo a la derecha de\(t = -\dfrac{\pi}{2}\) es consistente con la información de la Tabla 2.4. La gráfica de la

derecho también es consistente con la información de esta tabla en ambos lados de\(t = \dfrac{\pi}{2}\) y\(t = -\dfrac{\pi}{2}\)

El rango de la función tangente es el conjunto de todos los números reales.

Basado en la gráfica en (2), el periodo de la función tangente parece ser\(\pi\). El periodo es en realidad igual a\(\pi\), y se da más información al respecto en el Ejercicio (1).

Actividad 2.22 (La función tangente y el círculo unitario)

El diagrama de la Figura se\(\PageIndex{1}\) puede utilizar para mostrar cómo\(\tan(t)\) se relaciona con las definiciones de círculo unitario de\(\cos(t)\) y\(\sin(t)\).

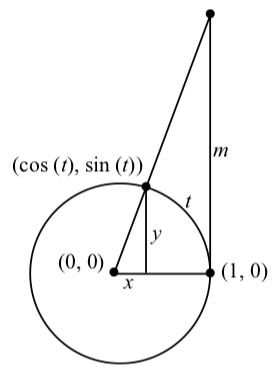
Figura\(\PageIndex{1}\): Ilustrando\(\tan(t)\) con el Círculo de Unidad

En el diagrama, se dibuja un arco de longitud t y\(\tan(t) = \dfrac{\cos(t)}{\sin(t)} = \dfrac{y}{x}\). Esto da la pendiente de la línea que pasa por los puntos\((0, 0)\) y\((\cos(t), \sin(t))\). La línea vertical a través del punto\((1, 0)\) cruza esta línea en el punto\((1, m)\). Esto quiere decir que la pendiente de esta línea también es m y por lo tanto, vemos que\[\tan(t) = \dfrac{\cos(t)}{\sin(t)} = m.\]

Ahora usa el applet Geogebra Generador de Gráfica Tangente para ver cómo se puede usar esta información para ayudar a ver cómo se puede generar la gráfica de la función tangente usando las ideas de la Figura\(\PageIndex{1}\). La dirección web es http://gvsu.edu/s/Zm

Efectos de Constantes en las Gráficas de la Función Tangente

Hay similitudes y algunas diferencias en los métodos de dibujar la gráfica de una función de la forma\(y = A\tan(B(t - C)) + D\) y dibujar la gráfica de una función de la forma\(y = A\sin(B(t - C)) + D\). Consulte la página 101 para obtener un resumen de los efectos de los parámetros\(A, B, C\), y\(D\) en la gráfica de una función sinusoidal.

Una de las diferencias al tratar con una función tangente (secante, cotangente o cosecante) es que no utilizamos la terminología específica de las ondas sinusoidales. En particular, no usaremos los términos amplitud y desplazamiento de fase. En lugar de amplitud, usamos el término más general estiramiento vertical (o compresión vertical), y en lugar de desplazamiento de fase, usamos el término más general desplazamiento horizontal. Exploraremos esta es la siguiente comprobación de progreso.

Ejercicio\(\PageIndex{2}\)

Considera la función cuya ecuación es\(y = 3\tan(2(x - \dfrac{\pi}{8})) + 1\). Incluso si usamos una utilidad gráfica para dibujar el gráfico, primero debemos responder las siguientes preguntas para obtener una ventana de visualización razonable para la utilidad gráfica. Podría ser una buena idea usar un método similar al que usaríamos si estuviéramos graficando\(y = 3\sin(2(x - \dfrac{\pi}{8})) + 1\)

1. Sabemos que para la sinusoide, el periodo es\(\dfrac{2\pi}{2}\). Sin embargo, el periodo de la función tangente es\(\pi\). Entonces, ¿cuál será el periodo de\(y = 3\tan(2(x - \dfrac{\pi}{8})) + 1\)?
2. Para la sinusoide, la amplitud es 3. Sin embargo, no utilizamos el término “amplitud” para la tangente. Entonces, ¿cuál es el efecto del parámetro 2 en la gráfica de\(y = 3\tan(2(x - \dfrac{\pi}{8})) + 1\)?
3. Para la sinusoide, el desplazamiento de fase es\(\dfrac{\pi}{8}\). Sin embargo, no utilizamos el término “desplazamiento de fase” para la tangente. Entonces, ¿cuál es el efecto del parámetro 8 en la gráfica de\(y = 3\tan(2(x - \dfrac{\pi}{8})) + 1\)?
4. Utilice una utilidad gráfica para dibujar la gráfica de esta función durante un periodo completo. Utilice el periodo de la función que contiene el número 0.

Contestar

1. La ecuación para la función es\(y = 3\tan(2(x - \dfrac{\pi}{8})) + 1\)
2. El periodo de esta función es\(\dfrac{\pi}{2}\).
3. El efecto del parámetro\(3\) es estirar verticalmente la gráfica de la función tangente.
4. A continuación se muestra una gráfica de un periodo de esta función utilizando\(-\dfrac{\pi}{8} \leq x \leq \dfrac{3\pi}{8}\) y\(-20 \leq y \leq 20\). Se muestran las asíntotas verticales, así como la línea horizontal\(y = 1\).\(x = -\dfrac{\pi}{8}\)\(x = \dfrac{3\pi}{8}\)

• El efecto del parámetro\(\dfrac{\pi}{8}\) es desplazar la gráfica de\(y = 3\tan(2(x)) + 1\) hacia la derecha por\(\dfrac{\pi}{8}\) unidades.

La Gráfica de la Función Secante

Para entender la gráfica de la función secante, necesitamos recordar la definición de la secante y las restricciones a su dominio. Si es necesario, consulte la Sección 1.6 para completar la siguiente verificación de progreso.

Ejercicio\(\PageIndex{3}\)

1. ¿Cómo se define la función secante?
2. ¿Cuál es el dominio de la función secante?
3. ¿Dónde tendrá asíntotas verticales la gráfica de la función secante?
4. ¿Cuál es el periodo de la función secante?

Contestar

La función secante es la recíproca de la función coseno. Es decir,\(\sec(t) = \dfrac{1}{\cos(t)}\)

El dominio de la función secante es el conjunto de todos los números reales\(t\) para los cuales\(t \neq \dfrac{\pi}{2} + k\pi\) para cada entero\(k\).

La gráfica de la función secante tendrá una asíntota vertical en aquellos valores de\(t\) que no estén en el dominio. Entonces habrá una asíntota vertical cuando\(t = \dfrac{\pi}{2} + k\pi\) para algún entero\(k\).

Ya que\(\sec(t) = \dfrac{1}{\cos(t)}\), y el periodo de la función coseno es\(2\pi\), concluimos que el periodo de la función secante es también\(2\pi\).

Actividad 2.25 (La Gráfica de la Función Secante)

Utilizaremos el Applet de Geogebra con la siguiente dirección web: http://gvsu.edu/s/Zn Este applet mostrará cómo se relaciona la gráfica de la función secante con la gráfica de la función coseno. En el applet,\(y = \cos(t)\) se muestra la gráfica de y se deja fija. Generamos puntos en la gráfica de\(y = \sec(t)\) usando el deslizador para t. Por cada valor de\(t\), se dibuja una línea vertical del punto\((t, \cos(t))\) al punto\((t, \sec(t))\). Observe cómo estos puntos indican que la gráfica de la función secante tiene asíntotas verticales en\(t = \dfrac{\pi}{2}, t = \dfrac{3\pi}{2}\) y\(\dfrac{5\pi}{2}\).

• Utilice una utilidad gráfica para dibujar la gráfica de\(y = \sec(t)\) usar\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\) y\(-10 \leq y \leq 10\). Nota: Puede ser necesario usar\(\sec(x) = \dfrac{1}{\cos(x)}\)
• Utilice una utilidad gráfica para dibujar la gráfica de\(y = \sec(t)\) usar\(-\dfrac{3\pi}{2} \leq x \leq \dfrac{3\pi}{2}\) y\(-10 \leq y \leq 10\).
• El trabajo en Actividad 2.25 y Figura\(\PageIndex{2}\) puede ser utilizado para ayudar a responder las preguntas en Ejercicio\(\PageIndex{3}\).

  

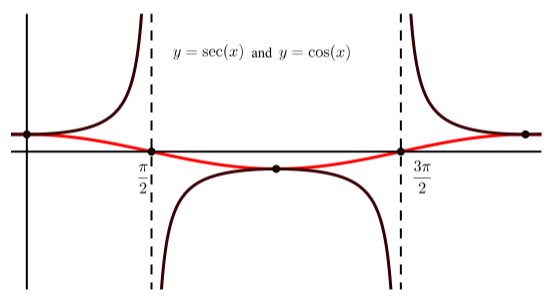
  Figura\(\PageIndex{2}\): Gráfica de un Periodo de\(y = \sec(t)\) con\(0 \ leq x \ leq 2\pi\)

Ejercicio\(\PageIndex{4}\)

1. ¿La gráfica de la Figura es\(\PageIndex{2}\) consistente con las gráficas de la Actividad 2.25?
2. ¿Por qué es la gráfica de\(y = \sec(t)\) arriba del eje x cuándo\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\)?
3. ¿Por qué está la gráfica de\(y = \sec(t)\) debajo del eje x cuando\(\dfrac{\pi}{2} \leq x \leq \dfrac{3\pi}{2}\)
4. ¿Cuál es el rango de la función secante?

Contestar

Todas las gráficas son consistentes.

Ya que\(\sec(x) = \dfrac{1}{\cos(x)}\), vemos que\(\sec(x) > 0\) si y sólo si\(\cos(x) > 0\). Entonces la gráfica de\(y = \sec(x)\) está por encima del\(x\) eje -si y sólo si la gráfica de\(y = \cos(x)\) está por encima del\(x\) -eje.

3. Ya que\(\sec(x) = \dfrac{1}{\cos(x)}\), vemos que\(\sec(x) < 0\) si y sólo si\(\cos(x) < 0\). Entonces la gráfica de\(y = \sec(x)\) está por debajo del\(x\) eje -si y sólo si la gráfica de\(y = \cos(x)\) está por encima del\(x\) -eje.

La clave es eso\(\sec(x) = \dfrac{1}{\cos(x)}\). Ya que\(-1 \leq \cos(x) \leq 1\), concluimos que\(\sec(x) \geq 1\) cuando\(\cos(x) > 0\) y\(\sec(x) \leq -1\) cuando\(\cos(x) < 0\). Dado que la gráfica de la función secante tiene asíntotas verticales, vemos que el rango de la función secante consiste en todos los números reales\(y\) para los cuales\(y \geq 1\) o\(y \leq -1\). Esto también se puede ver en la gráfica de\(y = \sec(x)\).

Resumen

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

La Función Tangente. El Cuadro 2.5 muestra algunas de las características importantes de la función tangente. Ya hemos discutido la mayoría de estos ítems, pero los dos últimos ítems de esta tabla serán explorados en Ejercicio (1) y Ejercicio (2). En la Figura se muestra una gráfica de tres periodos de la función tangente\(\PageIndex{3}\).

	\(y = \tan(t)\)	\(y = \sec(t)\)
periodo	\(\pi\)	\(2\pi\)
dominio	números reales\(t\) con\(t \neq \dfrac{\pi}{2}+k\pi\) para cada número entero\(k\)	números reales\(t\) con\(t \neq \dfrac{\pi}{2}+k\pi\) para cada número entero\(k\)
\(y\)-interceptar	\((0, 0)\)	\((0, 1)\)
\(x\)-intercepta	\(t = k\pi\), donde\(k\) hay algún número entero	ninguno
simetría	con respecto al origen	con respecto al\(y\) eje -

Tabla 2.5: Propiedades de las Funciones Tangente y Secante

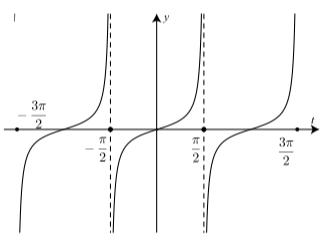
Figura\(\PageIndex{3}\): Gráfica de\(y = \tan(t)\)

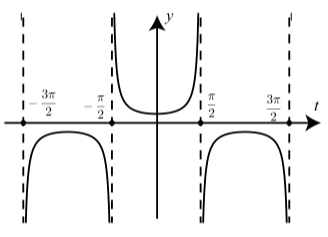
Figura\(\PageIndex{4}\): Gráfica de\(y = \sec(t)\)

La Función Secante. El Cuadro 2.5 muestra algunas de las características importantes de la función secante. La simetría de la función secante se explora en el Ejercicio (3). La Figura 2.29 muestra una gráfica de la función secante.

La Función Cosecante. La gráfica de la función cosecante se estudia de una manera similar a como estudiamos la gráfica de la función secante. Esto se hace en los Ejercicios (4), (5) y (6). En el Cuadro 2.6 se muestran algunas de las características importantes de la función cosecante. La simetría de la función cosecante se explora en el Ejercicio (3). La Figura 2.30 muestra una gráfica de la función cosecante.

La función cotangente. La gráfica de la función cosecante se estudia de una manera similar a como estudiamos la gráfica de la función tangente. Esto se hace en los Ejercicios (7), (8) y (9). En el Cuadro 2.6 se muestran algunas de las características importantes de la función cotangente. La simetría de la función cotangente se explora en el Ejercicio (3). La Figura 2.31 muestra una gráfica de la función cotangente.

	\(y = \csc(t)\)	\(y = \cot(t)\)
periodo	\ (y =\ csc (t)\) ">\(2\pi\)	\ (y =\ cuna (t)\) ">\(\pi\)
dominio	\ (y =\ csc (t)\) ">números reales\(t\) con\(t \neq k\pi\) para cada entero\(k\)	\ (y =\ cot (t)\) ">números reales\(t\) con\(t \neq k\pi\) para cada entero\(k\)
gama	\ (y =\ csc (t)\) ">\(|y| \geq 1\)	\ (y =\ cot (t)\) ">todos los números reales
\(y\)-interceptar	\ (y =\ csc (t)\) ">ninguno	\ (y =\ cot (t)\) ">ninguno
\(x\)-intercepta	\ (y =\ csc (t)\) ">ninguno	\ (y =\ cot (t)\) ">\(t = \dfrac{\pi}{2}+k\pi\) donde\(k\) es un entero
simetría	\ (y =\ csc (t)\) ">con respecto al origen	\ (y =\ cot (t)\) ">con respecto al origen

Tabla 2.6: Propiedades de las funciones cosecante y cotangente

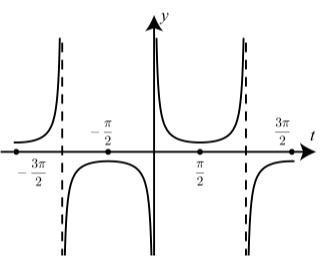
Figura\(\PageIndex{5}\): Gráfica de\(y = \csc(t)\)

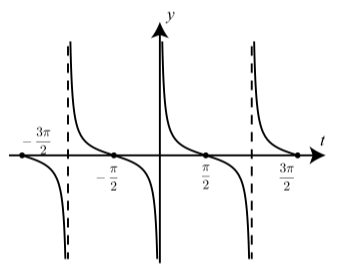
Figura\(\PageIndex{6}\): Gráfica de\(y = \cot(t)\)