2.5: Funciones trignométricas inversas

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Por qué la función sinusoidal no tiene realmente una inversa? ¿Qué queremos decir, entonces, con la función sinusoidal inversa? En otras palabras, ¿cómo se define la función sinusoidal inversa?
• ¿Cómo se define la función coseno inverso?
• ¿Cómo se define la función tangente inversa?

Actividad inicial

1. Si\(y = 5x + 7\) y\(y = 4\), ¿cuál es el valor de\(x\)?
2. Si\(y = \sqrt{x}\) y\(y = 2.5\), ¿cuál es el valor de\(x\)?
3. Si\(y = x^{2}\) y\(y = 25\), ¿cuáles son los valores posibles de\(x\)?
4. Si\(y = \sin(x)\) y\(y = 1\), encuentre dos valores para\(x\) con\(0 \leq x \leq 2.2\)

Introducción

El trabajo en la actividad inicial ilustra el problema general que si se nos da una función\(f\) y\(y = f(x)\), podemos encontrar los valores de\(x\) si conocemos el valor de\(y\). En efecto, esto significa que si conocemos el valor de\(y\), ¿podemos resolver por el valor de\(x\)? Para el primer problema, podemos\(y = 4\) sustituirlo\(y = 5x + 7\) y resolverlo\(x\). Esto da\[4 = 5x + 7\]\[-3 = 5x\]\[x = \dfrac{-3}{5}\]
Para el segundo y tercer problema, tenemos\[2.5 = \sqrt{x}\]\[2.5^{2} = (\sqrt{x})^{2}\]\[x = 6.25\]\[25 = \sqrt{x}\]\[x = \pm(\sqrt{25})\]\[x = \pm5\]
El trabajo con la ecuación\(x^{2} = 25\) muestra que podemos tener más de una solución para este tipo de problemas . Con funciones trigonométricas, incluso podemos tener más soluciones. Por ejemplo, si\(y = \sin(x)\) y\(y = \dfrac{1}{2}\), tenemos\[\sin(x) = \dfrac{1}{2}\]

Si restringimos los valores de\(0 \leq x \leq 2\pi\), habrá dos soluciones como se muestra en la Figura 2.32

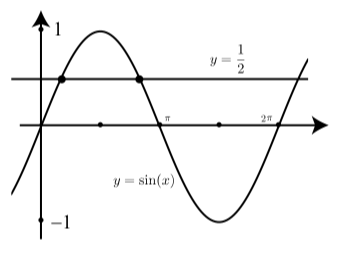
Figura\(\PageIndex{1}\): Gráfico que muestra\(\sin(x) = \dfrac{1}{2}\)

Desde nuestro conocimiento de los arcos comunes y arcos de referencia, estas dos soluciones son\(x = \dfrac{\pi}{6}\) y\(x = \dfrac{5\pi}{6}\). Además, la naturaleza periódica de la función sinusoidal nos dice que si no hay restricciones sobre\(x\), habrá infinitamente muchas soluciones de la ecuación\(\sin(x) = \dfrac{1}{2}\). Lo que queremos desarrollar es un método para indicar exactamente una de estas soluciones. Pero, ¿cuál elegimos?

Hemos hecho algo así cuando resolvemos una ecuación como\(x^{2} = 25\). Hay dos soluciones a esta ecuación, pero tenemos una función (la función de raíz cuadrada) que nos da exactamente una de estas dos funciones. Entonces cuando escribimos\(x = \sqrt{25} = 5\), estamos especificando sólo la solución positiva de la ecuación. Si queremos la otra solución, tenemos que escribir\(x = -\sqrt{25} = -5\). Observe que utilizamos la función raíz cuadrada para designar la “más simple” de las dos funciones, es decir, la solución positiva.

Para la función seno, lo que queremos es una función sinusoidal inversa que haga exactamente lo que sugiere el nombre, invierte de manera única lo que hace la función sinusoidal. Es decir, la función sinusoidal inversa toma un valor del rango de la función sinusoidal y nos da exactamente un arco cuyo seno tiene ese valor. Vamos a tratar de hacer esto de la manera más sencilla posible. (A veces puede ser difícil de creer, pero los matemáticos generalmente tratan de mantener las cosas simples). Para ser más específicos, si tenemos\(y = \sin(x)\), queremos poder especificar cualquier valor para\(y\) con\(-1 \leq y \leq 1\) y obtener un valor para\(x\). Vamos a elegir el valor para\(x\) que sea lo más cercano a 0 como sea posible. (Mantenlo simple.)

Entonces asegurar que solo haya una solución, vamos a restringir la gráfica de\(y = \sin(x)\) al intervalo\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\). Esto también garantiza que\(-1 \leq y \leq 1\) como se muestra en la Figura 2.33.

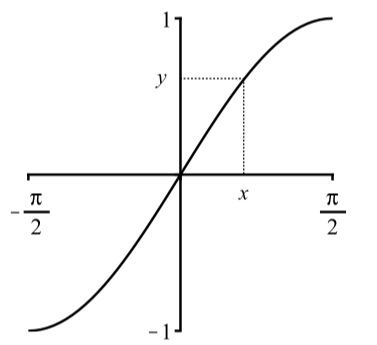
Figura\(\PageIndex{2}\): Gráfica de\(y = \sin(x)\) restringido a\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\)

Como se ilustra en la Figura\(\PageIndex{2}\), para cada valor de\(y\) con\(-1 \leq y \leq 1\), hay exactamente un valor de\(x\) con\(\sin(x) = y\) y\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\).

Definición

La función sinusoidal inversa (denotada por\(\arcsin\) o\(sin^{-1}\)), se define de la siguiente manera:
For\(-1 \leq y \leq 1\),\[t = \arcsin(y) \space or \space t = sin^{-1}(y)\] means\[y = \sin(t) \space and \space -\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}.\]

Precaución. Cualquiera de las dos notación puede ser utilizada para la función arcoseno. Es decir,\(\arcsin(y)\) y\(sin^{-1}(y)\)) significan lo mismo. Sin embargo, la notación\(sin^{-1}\)) no significa el recíproco del seno sino el inverso del seno con un dominio restringido. Es muy importante recordar los hechos de que el dominio del seno inverso es el intervalo\([-1, 1]\) y el rango del seno inverso es el intervalo\([-\dfrac{\pi}{2}, \dfrac{\pi}{2}].\)

Nota

Algunas personas prefieren usar\(t = \arcsin(y)\) en lugar de\(t = sin^{-1}(y)\)) ya que puede ser un recordatorio de lo que significa la notación. La ecuación\(t = \arcsin(y)\) es una abreviatura para\(t\) es el arco con valor sinusoidal\(y\) y\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\).

Es importante seguir escribiendo la restricción\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\) ya que es importante darse cuenta de que la\(\arcsin(y)\) función da sólo un arco cuyo valor sinusoidal es\(y\) y\(t\) debe estar en este intervalo.

Ejemplo\(\PageIndex{1}\): Inverse Sine Function

Determinaremos el valor exacto de\(\arcsin(\dfrac{\sqrt{3}}{2})\). Así que dejamos\(t = \arcsin(\dfrac{\sqrt{3}}{2})\)

Esto significa que\[\sin(t) = \dfrac{\sqrt{3}}{2}\] y\[-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}.\]

Es decir, estamos tratando de encontrar el arco t cuyo seno es\(\dfrac{\sqrt{3}}{2}\) y\(-\dfrac{\pi}{2} \leq y \leq \dfrac{\pi}{2}\). Usando nuestro conocimiento de los valores sinusoidales para arcos comunes, lo notamos\(\sin(\dfrac{\pi}{3}) = \dfrac{\sqrt{3}}{2}\) y así concluimos que\(t = \dfrac{\pi}{3}\) o aquello\[\arcsin(\dfrac{\sqrt{3}}{2}) = \dfrac{\pi}{3}\]

Esto se ilustra gráficamente en la Figura\(\PageIndex{3}\).

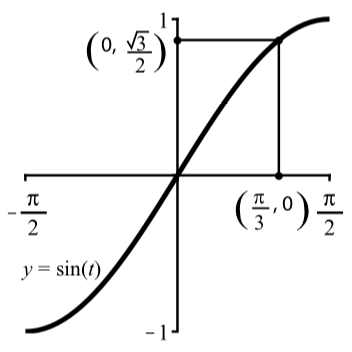
Figura\(\PageIndex{3}\): Versión gráfica de\(\arcsin(\dfrac{\sqrt{3}}{2}) = \dfrac{\pi}{3}\)

Nota: La mayoría de las calculadoras y utilidades gráficas pueden calcular valores aproximados para la función sinusoidal inversa. En las calculadoras, suele ser la\(\sin^{-1}\) clave y para muchos programas informáticos, es necesario escribir “arcsin”. Usando una calculadora, vemos eso\(\arcsin(\dfrac{\sqrt{3}}{2}) \approx 1.04720\), que es una aproximación decimal para\(\dfrac{\pi}{3}\).

Ejercicio\(\PageIndex{1}\)

1. \(\arcsin(-\dfrac{\sqrt{3}}{2})\)
2. \(\sin^{-1}(\dfrac{1}{2})\)
3. \(\arcsin(-1)\)
4. \(\arcsin(-\dfrac{\sqrt{2}}{2})\)

En la siguiente comprobación de progreso, utilizaremos la función sinusoidal inversa en cálculos de dos pasos. Por favor, preste atención a los resultados que se obtengan.

Responder

1. \(\arcsin(-\dfrac{\sqrt{3}}{2}) = -\dfrac{\pi}{3}\)desde\(\sin(-\dfrac{\pi}{3}) = -\dfrac{\sqrt{3}}{2}\) y\(-\dfrac{\pi}{2} \leq -\dfrac{\pi}{3} \leq \dfrac{\pi}{2}\).

2. \(\sin^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{6}\)desde\(\sin(\dfrac{\pi}{2}) = -\dfrac{1}{2}\) y\(-\dfrac{\pi}{2} \leq \dfrac{\pi}{6} \leq \dfrac{\pi}{2}\).

3. \(\arcsin(-1) = -\dfrac{\pi}{2}\)desde\(\sin(-\dfrac{\pi}{2}) = -1\) y\(-\dfrac{\pi}{2} \leq -\dfrac{\pi}{2} \leq \dfrac{\pi}{2}\).

4. \(\arcsin(-\dfrac{\sqrt{2}}{2}) = -\dfrac{\pi}{4}\)desde\(\sin(-\dfrac{\pi}{4}) = -\dfrac{\sqrt{2}}{2}\) y\(-\dfrac{\pi}{2} \leq -\dfrac{\pi}{4} \leq \dfrac{\pi}{2}\).

Ejercicio\(\PageIndex{2}\)

Determinar el valor exacto de cada uno de los siguientes. Puedes consultar tus resultados con una calculadora.

1. \(\sin(\sin^{-1}(\dfrac{1}{2}))\)
2. \(\arcsin(\sin(\dfrac{\pi}{4}))\)
3. \(\sin(\sin^{-1}(\dfrac{1}{2}))\)
4. \(\arcsin(\sin(\dfrac{3\pi}{4}))\)

Responder

1. Ya que\(\sin^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{6}\), vemos que\(\sin(\sin^{-1}(\dfrac{1}{2})) = \sin(\dfrac{\pi}{6}) = \dfrac{1}{2}\)

2. \(\arcsin(\sin(\dfrac{\pi}{4})) = \arcsin(\dfrac{\sqrt{2}}{2})\). Además,\(\arcsin(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}\) desde\(\sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}\) y\(-\dfrac{\pi}{2} \leq -\dfrac{\pi}{4} \leq \dfrac{\pi}{2}\). Entonces vemos que\[\arcsin(\sin(\dfrac{\pi}{4})) = \arcsin(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}.\]

3. No conocemos un valor exacto para\(\sin^{-1}(\dfrac{2}{5})\). Entonces dejamos\(t = \sin^{-1}(\dfrac{2}{5})\).

Entonces sabemos eso\(\sin(t) = \dfrac{2}{5}\) y\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\) .Entonces

\[\sin(\sin^{-1}(\dfrac{2}{5})) = \sin(t) = \dfrac{2}{5}\]

4. \(\arcsin(\sin(\dfrac{\pi}{4})) = \arcsin(\dfrac{\sqrt{2}}{2})\). Además,\(\arcsin(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}\) desde\(\sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}\) y\(-\dfrac{\pi}{2} \leq \dfrac{\pi}{4} \leq \dfrac{\pi}{2}\). Entonces vemos que\[\arcsin(\sin(\dfrac{\pi}{4})) = \arcsin(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}\]

El trabajo en Ejercicio\(\PageIndex{2}\) ilustra algunas propiedades importantes de la inversa desde la función cuando se compone con la función seno. Esta propiedad es que en algún sentido, el seno inverso y las funciones sinusoidales se “deshacen” entre sí. Para ver lo que esto significa, dejamos\(y = \sin(t)\) con\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\). Entonces\[\sin^{-1}(\sin(t)) = \sin^{-1}(y) = t\] por definición. Esto significa que si aplicamos el seno, entonces el seno inverso a un arco entre\(-\dfrac{\pi}{2}\) y\(\dfrac{\pi}{2}\), recuperamos el arco. Esto es lo que queremos decir cuando decimos que el seno inverso deshace el seno.
Del mismo modo, si\(t = \sin^{-1}(y)\) para algunos\(y\) con\(-1 \leq y \leq 1\), entonces\[\sin(\sin^{-1}(y)) = \sin(t) = y\] por definición. Entonces el seno también deshace el seno inverso también. Resumimos estos dos resultados de la siguiente manera:

Propiedades de la Función Sinusoidal Inversa

• Por cada t en el intervalo cerrado\([-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\),\[\sin^{-1}(\sin(t)) = t.\]
• Por cada y en el intervalo cerrado\([-1, 1]\),\[\sin(\sin^{-1}(y)) = y.\]

Las funciones de coseno inverso y tangente inversa

De manera similar a como definimos la función sinusoidal inversa, podemos definir las funciones coseno inverso y tangente inversa. La clave es restringir el dominio de la función circular correspondiente para que obtengamos la gráfica de una función uno a uno. Entonces usaremos\(y = \cos(t)\) con\(0 \leq t \leq \pi\) y\(y = \tan(t)\) con\(-\dfrac{\pi}{2} < t < \dfrac{\pi}{2}\) como se ilustra en la Figura\(\PageIndex{4}\).

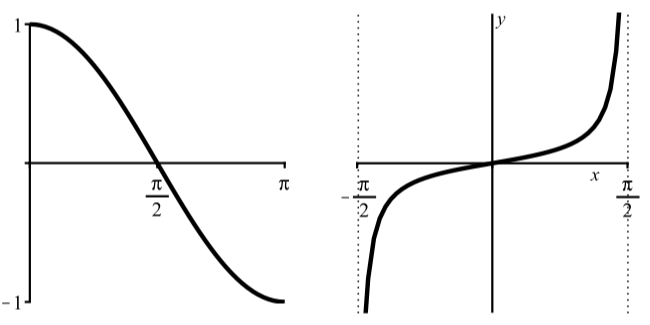
Figura\(\PageIndex{4}\): Gráfica de\(y = \cos(t)\) para\(0 \leq t \leq \pi\) y Gráfica de\(y = \tan(t)\) para\(-\dfrac{\pi}{2} < t < \dfrac{\pi}{2}\).

Nota

No usamos el intervalo\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\) para la función coseno ya que la función coseno no es uno a uno en ese intervalo. Además, el intervalo para la función tangente no contiene los puntos finales ya que la función tangente no está definida en y\(-\dfrac{\pi}{2}\) y\(\dfrac{\pi}{2}\).

Usando estos dominios, ahora definimos las funciones inversas para coseno y tangente.

Definición

La función coseno inversa (denotada por\(\arccos\) o\(cos^{-1}\)), se define de la siguiente manera:
For\(-1 \leq y \leq 1\),\[t = \arccos(y) \space or \space t = cos^{-1}(y)\] to mean\[y = \cos(t) \space and \space 0 \leq x \leq \pi.\]

Definimos la función tangente inversa (denotada por\(\arctan\) o\(tan^{-1}\)), de la siguiente manera:
For\(t \in \mathbb{R}\),\[t = \arctan(y) \space or \space t = tan^{-1}(y)\] means\[y = \tan(t) \space and \space -\dfrac{\pi}{2} < x < \dfrac{\pi}{2}.\]

Nota

Los resultados anteriores se pueden escribir usando la función arcsine en lugar de\(\sin^{-1}\). Es muy importante darse cuenta que estos resultados son válidos solo para\ (-\ dfrac {\ pi} {2}\ leq x leq\ dfrac {\ pi} {2}\] y\[-1 \leq y \leq 1.\]

Ejemplo\(\PageIndex{2}\): An Example of Inverse Cosine

La ecuación\(y = \arccos(-\dfrac{1}{2}) = \cos^{-1}(-\dfrac{1}{2})\) significa que\(\cos(y) = -\dfrac{1}{2}\) y\(0 \leq y \leq \pi\).

Es decir, estamos tratando de encontrar el arco\(y\) cuyo coseno es\(0 \leq y \leq \pi\). Utilizando nuestro conocimiento de los valores de coseno para arcos comunes, notamos que\(\cos(\dfrac{\pi}{3}) = \dfrac{1}{2}.\) Así concluimos que el ángulo de referencia\(\hat{y}\) para\(y\) es\(\hat{y} = \dfrac{\pi}{3}\). Ya que\(y\) debe estar en la QII, concluimos que\(y = \pi - \dfrac{\pi}{3}\) o\(y = \dfrac{2\pi}{3}\). Entonces\[\arccos(-\dfrac{1}{2}) = \dfrac{2\pi}{3}.\]

Esto se puede verificar usando una calculadora y se ilustra en la Figura\(\PageIndex{5}\).

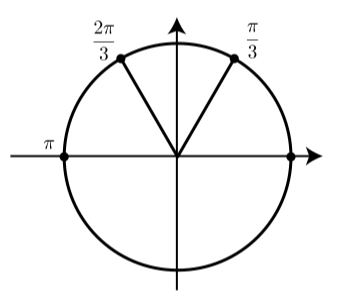
Figura\(\PageIndex{5}\): Diagrama utilizado para el coseno inverso de\(-\dfrac{1}{2}\).

Ejercicio\(\PageIndex{3}\)

Determinar el valor exacto de cada uno de los siguientes. Puedes consultar tus resultados con una calculadora.

1. \(\cos(\cos^{-1}(\dfrac{1}{2}))\)
2. \(\arccos(\cos(\dfrac{\pi}{4}))\)
3. \(\arccos(\cos(\dfrac{-\pi}{4}))\)
4. \(\tan^{-1}(\tan(\dfrac{5\pi}{4}))\)

El trabajo en Ejercicio\(\PageIndex{2}\) ilustra algunas propiedades importantes del coseno inverso y las funciones tangentes inversas similares a las propiedades de la función sinusoidal inversa en la página 147.

Responder

1. Ya que\(\cos^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{3}\), vemos eso\(\cos(\cos^{-1}(\dfrac{1}{2})) = \cos(\dfrac{\pi}{3}) = \dfrac{1}{2}\).

2. \(\arccos(\cos(\dfrac{\pi}{4})) = \arccos(\dfrac{\sqrt{2}}{2})\). Además,\(\arccos(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}\) desde\(\cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}\) y\(0 \leq \dfrac{\pi}{4} \leq \pi\). Entonces vemos que\[\arccos(\cos(\dfrac{\pi}{4})) = \arccos(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}.\]

3. \(\arccos(\cos(-\dfrac{\pi}{4})) = \arccos(\dfrac{\sqrt{2}}{2})\). Además,\(\arccos(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}\) desde\(\cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}\) y\(0 \leq \dfrac{3\pi}{4} \leq \pi\). Entonces vemos que\[\arccos(\cos(-\dfrac{\pi}{4})) = \arccos(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}.\]

4. \(\tan^{-1}(\tan(\dfrac{5\pi}{4})) = \tan^{-1}(1)\). Además,\(\tan^{-1}(1) = \dfrac{\pi}{4}\) desde\(\tan(\dfrac{\pi}{4}) = 1\) y\(-\dfrac{\pi}{2} \leq \dfrac{\pi}{4} \leq \dfrac{\pi}{2}\). Entonces vemos que\[\tan^{-1}(\tan(\dfrac{5\pi}{4})) = \tan^{-1}(1) = \dfrac{\pi}{4}\]

Propiedades de la Función Coseno Inversa

• Para cada uno\(t\) en el intervalo cerrado\([0, \pi]\):\[\cos^{-1}(\cos(t)) = t\]
• Para cada uno\(y\) en el intervalo cerrado\([-1, 1]\):\[\cos(\cos^{-1}(y)) = y\]

Propiedades de la Función Tangente Inversa

• Para cada uno\(t\) en el intervalo abierto\((-\dfrac{\pi}{2}, \pi)\):\[\tan^{-1}(\tan(t)) = t\]
• Por cada número real\(y\):\[\tan(\tan^{-1}(y)) = y\]

La justificación de estas propiedades se incluye en los ejercicios.

Ejercicio\(\PageIndex{4}\)

Determine el valor exacto de cada uno de los siguientes y verifíquelos usando una calculadora.

1. \(y = \arccos(1)\)
2. \(y = \tan^{-1}(\sqrt{3})\)
3. \(y = \arctan(-1)\)
4. \(y = \cos^{-1}(-\dfrac{\sqrt{2}}{2})\)
5. \(\sin(\arccos(-\dfrac{1}{2}))\)
6. \(\tan(\arcsin(-\dfrac{\sqrt{3}}{2}))\)
7. \(\arccos(\sin(\dfrac{\pi}{6}))\)

Cuando evaluamos una expresión como\(\sin(\arccos(-\dfrac{1}{2}))\) en la actividad previa previa, podemos usar el hecho de que es posible determinar el valor exacto de\(\arccos(-\dfrac{1}{2})\) para completar el problema. Si se nos da un problema similar pero no conocemos el valor exacto de una función trigonométrica inversa, a menudo podemos usar la Identidad Pitagórica para ayudar. Esto lo haremos en la próxima comprobación de progreso.

Responder

1. \(y = \arccos(1) = 0\)
2. \(y = \tan(\sqrt{3}) = \dfrac{\pi}{3}\)
3. \(y = \arctan(-1) = -\dfrac{\pi}{4}\)
4. \(y = \cos^{-1}(-\dfrac{\sqrt{2}}{2}) = \dfrac{3\pi}{4}\)
5. \(\sin(\arccos(\dfrac{1}{2})) = \dfrac{\sqrt{3}}{2}\)
6. \(\tan(\arcsin(-\dfrac{\sqrt{3}}{2})) = -\sqrt{3}\)
7. \(\arccos(\sin(\dfrac{\pi}{6})) = \dfrac{\pi}{3}\)

Ejercicio\(\PageIndex{5}\)

1. Determinar el valor exacto de\(\sin(\arccos(\dfrac{1}{3}))\). A continuación se sugiere una forma de iniciar esto. Como no conocemos el valor exacto de\(\arccos(\dfrac{1}{3})\), empezamos por dejar\(t = \arccos(\dfrac{1}{3})\). Entonces sabemos eso\(\cos(t) = \dfrac{1}{3}\) y\(0 \leq t \leq \pi\). Observe eso\(\sin(t) = \sin(\arccos(\dfrac{1}{3}))\). Entonces, para completar el problema, determinar el valor exacto de\(\sin(t)\) usar la Identidad Pitagórica teniendo en cuenta eso\(0 \leq t \leq \pi\).
2. Determinar el valor exacto de\(\cos(\arcsin(-\dfrac{4}{7}))\)

Responder

1. Vamos\(t = \arccos(\dfrac{1}{3})\). Entonces sabemos eso\[\cos(t) = \dfrac{1}{3}\] y\[0 \leq t \leq \pi\]
Usando la Identidad Pitagórica, vemos eso\((\dfrac{1}{3})^{2} + \sin^{2}(t) = 1\) y esto implica eso\(\sin^{2}(t) = \dfrac{8}{9}\). Ya que\(0 \leq t \leq \pi\),\(t\) está en el segundo cuadrante y en ambos cuadrantes,\(\sin(t) > 0\). Entonces,\(\sin(t) = \dfrac{\sqrt{8}}{3}\). Es decir,\ [\ sin (\ arccos (\ dfrac {1} {3})) =\ dfrac {\ sqrt {8}} {3}\).

2. Para\(\cos(\arcsin(-\dfrac{4}{7}))\), dejamos\(t = \arcsin(-\dfrac{4}{7})\). Esto significa que

\[\sin(t) = -\dfrac{4}{7}\]y\[-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}.\]
Podemos utilizar la Identidad Pitagórica para obtener\(\cos^{2}(t) + (-\dfrac{4}{7})^{2} = 1\). Esto da\(\cos^{2}(t) = \dfrac{33}{49}\). También tenemos la restricción\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\) y sabemos\(\sin(t) < 0\). Esto quiere decir que\(t\) debe estar en\(QIV\) y así\(\cos(t) > 0\). De ahí,\(\cos(t) = \dfrac{\sqrt{33}}{7}\). Es decir,

\[\cos(\arcsin(-\dfrac{4}{7})) = \dfrac{\sqrt{33}}{7}\]

Nota: Puedes usar tu calculadora para verificar este trabajo. Usa tu calculadora para aproximar tanto\(\cos(\arcsin(-\dfrac{4}{7}))\) y\(\dfrac{\sqrt{33}}{7}\). Ambos resultados deben ser\(0.8206518066\).

Resumen

En esta sección, estudiamos los siguientes conceptos e ideas importantes:

• La función sinusoidal inversa invierte de manera única lo que hace la función sinusoidal. La función sinusoidal inversa toma un valor\(y\) del rango de la función sinusoidal y nos da exactamente un número real t cuyo seno es igual a\(y\). Es decir, si\(y\) es un número real y\(-1 \leq y \leq 1\), entonces\(\sin^{-1}(y) = t\) significa que\(\sin(t) = y\) y\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\). Además, la función sinusoidal inversa satisface las siguientes propiedades importantes:

1. Para cada uno\(t\) en el intervalo cerrado\([-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\),\[\sin^{-1}(\sin(t)) = t\]
2. Para cada uno\(y\) en el intervalo cerrado\([-1, 1]\),\[\sin(\sin^{-1}(y)) = y\]

• La función de coseno inverso invierte de manera única lo que hace la función coseno. La función coseno inversa toma un valor\(y\) del rango de la función coseno y nos da exactamente un número real\(t\) cuyo coseno es igual a\(y\). Es decir, si\(y\) es un número real y\(-1 \leq y \leq 1\), entonces\(\cos^{-1}(y) = t\) significa que\(\cos(t) = y\) y\(0 \leq t \leq \pi\). Además, la función coseno inverso satisface las siguientes propiedades importantes:

1. Para cada uno\(t\) en el intervalo cerrado\([0, \pi]\),\[\cos^{-1}(\cos(t)) = t\]
2. Para cada uno\(y\) en el intervalo cerrado\([-1, 1]\),\[\cos(\cos^{-1}(y)) = y\]

• La Función Tangente Inversa invierte de manera única lo que hace la función tangente. La función tangente inversa toma un valor\(y\) del rango de la función tangente y nos da exactamente un número real\(t\) cuya tangente es igual a\(y\). Es decir, si\(y\) es un número real, entonces\(\tan^{-1}(y) = t\) significa que\(\tan(t) = y\) y\(-\dfrac{\pi}{2} < x < \dfrac{\pi}{2}\). Además, la función tangente inversa satisface las siguientes propiedades importantes:

1. Para cada uno\(t\) en el intervalo abierto\((-\dfrac{\pi}{2}, \dfrac{\pi}{2})\),\[\tan^{-1}(\tan(t)) = t\]
2. Por cada número real\(y\),\[\tan(\tan^{-1}(y)) = y\]