2.6: Resolver ecuaciones trigonmétricas

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

Para estas preguntas, dejamos\(q\) ser un número real con\(-1 \leq q \leq 1\) y dejar\(r\) ser un número real.

• ¿Cómo se puede utilizar una función trigonométrica inversa para determinar una solución de una ecuación de la forma\(\sin(x) = q, \cos(x) = q\), o\(\tan(x) = r\)?
• ¿Cómo pueden utilizarse las propiedades de las funciones trigonométricas para determinar todas las soluciones de una ecuación de la forma\(\sin(x) = q, \cos(x) = q\), o\(\tan(x) = r\)? dentro de un periodo completo de la función trigonométrica?
• ¿Cómo podemos usar el periodo de una función trigonométrica para determinar una fórmula para las soluciones de una ecuación de la forma\(\sin(x) = q, \cos(x) = q\), o\(\tan(x) = r\)?

Recordemos que una ecuación matemática como\(x^{2} = 1\) es una relación entre dos expresiones que puede ser cierta para algunos valores de la variable mientras que una identidad like\(\cos(-x) = \cos(x)\) es una ecuación que es verdadera para todos los valores permitidos de la variable. Entonces una identidad es un tipo especial de ecuación. Las ecuaciones que no son identidades también se denominan ecuaciones condicionales porque no son válidas para todos los valores permitidos de la variable. Resolver una ecuación significa encontrar todos los valores para las variables que hacen que las dos expresiones a cada lado de la ecuación sean iguales entre sí. Resolvimos ecuaciones algebraicas en álgebra y ahora resolveremos ecuaciones trigonométricas.

Una ecuación trigonométrica es una ecuación que involucra funciones trigonométricas. Ya hemos utilizado métodos gráficos para aproximar soluciones de ecuaciones trigonométricas. En el Ejemplo 2.17, usamos la función

\[V(t) = 35\cos \left(\dfrac{5\pi}{3}t \right) + 105\]

como modelo para la cantidad de sangre en el corazón. Para esta función, t se mide en segundos ya que el corazón estaba lleno y V .t/se mide en mililitros. Para determinar los tiempos en que hay 140 mililitros de sangre en el corazón, necesitábamos resolver la ecuación

\[35\cos \left(\dfrac{5\pi}{3}t \right) + 105 = 100\]

En ese momento, se utilizó la capacidad de “intersección” de una utilidad gráfica para determinar algunas soluciones de esta ecuación. En esta sección, aprenderemos a usar la función coseno inverso y las propiedades de la función coseno para determinar las soluciones de esta ecuación. Comenzamos por estudiar primero ecuaciones más simples.

Actividad inicial

Utilice una utilidad gráfica para dibujar las gráficas de\(y = \cos(x)\) y\(y = 0.7\) sobre los mismos ejes usando\(-\pi \leq x \leq \pi\) y\(-1.2 \leq y \leq 1.2\). Utilice la utilidad gráfica para encontrar los puntos de intersección de estas dos gráficas y determinar soluciones de la ecuación\(\cos(x) = 0.7\)

En la actividad inicial, deberíamos haber determinado las siguientes aproximaciones para soluciones de la ecuación\(\cos(x) = 0.7\):

• \(x_{1} \approx 0.79540\)
• \(x_{1} \approx -0.79540\)

Estas aproximaciones se han redondeado a cinco decimales.

La gráfica a continuación muestra las dos gráficas que utilizan\(-3\pi \leq x \leq 3\pi\). Las soluciones\(x_{1}\) y\(x_{2}\) se muestran en la gráfica. Como se puede ver, la gráfica muestra\(x_{1}\) y\(x_{2}\) y otras cuatro soluciones a la ecuación\(\cos(x) = 0.7\). De hecho, si imaginamos que la gráfica se extendió indefinidamente hacia la izquierda y hacia la derecha, podemos ver que hay infinitamente muchas soluciones para esta ecuación.

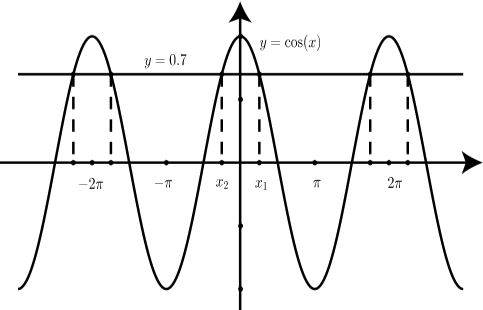
Aquí es donde podemos usar el hecho de que está el periodo de la función coseno\(2\pi\). Las otras soluciones difieren de\(x_{1}\) o\(x_{2}\) por un múltiplo entero del período de\(2\pi\). Podemos representar un múltiplo entero de\(2\pi\) por\(k(2\pi)\) para algún entero\(k\). Entonces decimos que cualquier solución de la ecuación\(\cos(x) = 0.7\) puede aproximarse por

\[x_{1} \approx 0.79540 + k(2\pi)\]

o

\[x_{1} \approx -0.79540 + k(2\pi)\]

Por ejemplo, si usamos\(k = 4\), vemos eso\(x \approx 25.92814\) o\(x \approx 24.33734\).

Podemos usar una calculadora para verificar eso para ambos valores,\(\cos(x) = 0.7\).

Una estrategia para resolver una ecuación trigonométrica

El ejemplo usando la ecuación\(\cos(x) = 0.7\) fue diseñado para ilustrar el hecho de que si no hay restricciones impuestas a lo desconocido\(x\), entonces puede haber infinitamente muchas soluciones para una ecuación de la forma “alguna función trigonométrica de\(x\)” = un número.

Una estrategia general para resolver tales ecuaciones es:

• Encuentra todas las soluciones de la ecuación dentro de un periodo de la función. Esto a menudo se hace mediante el uso de propiedades de la función trigonométrica. Muy a menudo, habrá dos soluciones dentro de un solo periodo.
• Utilice el período de la función para expresar fórmulas para todas las soluciones agregando múltiplos enteros del período a cada solución encontrada en el primer paso. Por ejemplo, si la función tiene un periodo de\(2\pi\) y\(x_{1}\) y\(x_{2}\) son las dos únicas soluciones en un periodo completo, entonces escribiríamos las soluciones para la ecuación como\[x = x_{1} + k(2\pi), x = x_{2} + k(2\pi)\], donde\(k\) es un entero.

Nota

En lugar de escribir “\(k\)es un entero”, podríamos escribir\[k \in \{\dotsb, -2, -1, 0, 1, 2, \dotsb\}.\]

Ejercicio\(\PageIndex{1}\)

Utilice una gráfica para aproximar las soluciones (redondeadas a cuatro decimales) de la ecuación\(\sin(x) = -0.6\) en el intervalo\(-\pi \leq x \leq \pi\). Luego usa el periodo de la función sinusoidal para escribir fórmulas que puedan ser utilizadas para aproximar cualquier solución de esta ecuación.

Responder

Cualquier solución de la ecuación\(\sin(x) = -0.6\) puede aproximarse con una de las siguientes:

\[x \approx 0.64350 + k(2\pi)\]o\[x \approx 2.49809 + k(2\pi)\]

Uso de funciones inversas para resolver ecuaciones trigonométricas

Aunque podemos usar una utilidad gráfica para determinar aproximaciones para soluciones a muchas ecuaciones, a menudo necesitamos tener alguna notación para indicar números específicos (que a menudo son soluciones de ecuaciones). Esto ya lo hemos visto en cursos previos de matemáticas. Por ejemplo, usamos la notación\(\sqrt{20}\) para representar el número real positivo cuyo cuadrado es igual a\(20\). Podemos usar esto para decir que las dos soluciones de la ecuación\(x^{2} = 20\) son\[x = \sqrt{20} \space and \space x = -\sqrt{20}\]

Observe que hay dos soluciones de la ecuación pero\(\sqrt{20}\) representa sólo una de esas soluciones. Ahora aprenderemos a usar las funciones trigonométricas inversas para hacer algo similar para las ecuaciones trigonométricas. Una gran diferencia es que la mayoría de las ecuaciones trigonométricas tendrán infinitamente muchas soluciones en lugar de solo dos. Utilizaremos las funciones trigonométricas inversas para representar una solución de una ecuación y luego aprenderemos a representar todas las soluciones en términos de esta única solución. Primero mostraremos cómo se hace esto con la ecuación\(\cos(x) = 0.7\) desde la actividad inicial para esta sección.

Ejemplo\(\PageIndex{1}\): Solving an Equation Involving the Cosine Function

Para la ecuación\(\cos(x) = 0.7\), primero usamos el resultado sobre la función coseno inverso en la página 150, que establece que para\(t\) en el intervalo cerrado\([0, \pi]\),\[\cos^{-1}(\cos(t)) = t\]

Así que “aplicamos la función coseno inversa” a ambos lados de la ecuación\(\cos(x) = 0.7\) Esto da:

\[\cos(x) = 0.7\]

\[\cos^{-1}(\cos(x)) = \cos^{-1}(0.7)\]

\[x = \cos^{-1}(0.7) \nonumber\]

Otra cosa que debemos recordar es que esto da la única solución para la ecuación que está en intervalo\([0, \pi]\). Antes de usar la propiedad periódica, necesitamos determinar las otras soluciones para la ecuación en un periodo completo de la función coseno. Podemos usar el intervalo\([0, 2\pi]\) pero es más fácil usar el intervalo\([-\pi, \pi]\). Una de las razones de ello es la siguiente llamada “identidad de arco negativo” declarada en p edad 82.

\ [\ cos (-x) =\ cos (x)\) por cada número real\(x\).

De ahí que ya que una solución para la ecuación es\(x = \cos^{-1}(0.7)\), otra solución es\(x = -\cos^{-1}(0.7)\). Esto significa que las dos soluciones de la ecuación\(x = \cos(x)\) en el intervalo\([-\pi, \pi]\) son

\[x = \cos^{-1}(0.7) \space and \space x = -\cos^{-1}(0.7) \nonumber\]

Se puede verificar que la ecuación\(\cos(x) = 0.7\) tiene dos soluciones en el intervalo\([-\pi, \pi]\) dibujando las gráficas de\(y = \cos(x)\) y\(y = 0.7\) sobre el intervalo\([-\pi, \pi]\). Entonces, si nos limitamos a este intervalo, tenemos algo muy parecido a resolver la ecuación\(x^{2} = 20\) en que hay dos soluciones que son negativas entre sí. La principal diferencia ahora es que la ecuación trigonométrica tiene infinitamente muchas soluciones y como antes, ahora usamos la propiedad periódica de la función coseno. Ya que el periodo es\(2\pi\), al igual que con las aproximaciones numéricas desde la actividad inicial, podemos decir que cualquier solución de la ecuación\(\cos(x) = 0.7\) será de la forma

\[x = \cos^{-1}(0.7) + k(2\pi) \space or \space x = -\cos^{-1}(0.7) + k(2\pi) \nonumber\]

donde\(k\) es algún número entero.

Ejercicio\(\PageIndex{2}\)

Determinar todas las soluciones de la ecuación\(4\cos(x) + 3 = 2\) en el intervalo\([-\pi, \pi]\). Luego usa la propiedad periódica de la función coseno para escribir fórmulas que puedan ser utilizadas para generar todas las soluciones de esta ecuación.

Pista

Primero usa álgebra para reescribir la ecuación en la forma\(\cos(x)\) = “algún número”.

Responder

Primero reescribimos la ecuación de la\(4\cos(x) + 3 = 2\) siguiente manera:

\[\begin{align*} 4\cos(x) + 3 &= 2 \\[4pt] 4\cos(x) &= -1 \\[4pt] \cos(x) &= -\dfrac{1}{4} \end{align*}\]

Entonces en el intervalo\([-\pi, \pi]\), las soluciones son\(x_{1} = \arccos(-\dfrac{1}{4})\) y\(x_{2} = -\arccos(-\dfrac{1}{4})\). Entonces cualquier solución de la ecuación\(4\cos(x) + 3 = 2\) es de la forma

\[x = \arccos(-\dfrac{1}{4}) + k(2\pi)\]o\[x = -\arccos(-\dfrac{1}{4}) + k(2\pi) \nonumber\]

Los ejemplos anteriores han demostrado que al usar la función coseno inverso para resolver ecuaciones de la forma\(\cos(x)\) = un número, es más fácil usar el intervalo\([-\pi, \pi]\); en lugar del intervalo\([0, 2\pi]\). Esto no es necesariamente cierto cuando se usa la función sinusoidal inversa ya que la función sinusoidal inversa da un valor en el intervalo\([-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\). Sin embargo, para mantener las cosas similares, seguiremos usando el intervalo\([-\pi, \pi]\); como el periodo completo para la función seno (o coseno). Para el seno inverso, utilizamos la siguiente propiedad indicada en la página 147.

Por cada t en el intervalo cerrado\([-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\),\[\sin^{-1}(sin(t)) = t\]

Al resolver ecuaciones que involucran la función coseno, también usamos una identidad de arco negativo. Hacemos lo mismo y utilizaremos la siguiente identidad de arco negativo que se indica en la página 82. \[\sin(-x) = -\sin(x)\]por cada número real\(x\).

Ejemplo\(\PageIndex{2}\): Solving an Equation Involving the Sine Function

Ilustraremos el proceso general utilizando la ecuación\(\sin(x) = -0.6\) de la Comprobación de Progreso 2.34. Debido a la identidad de arco negativo para la función sinusoidal, en realidad es más fácil trabajar con la ecuación\(\sin(x) = 0.6\). Esto se debe a que si\(x = a\) es una solución de la ecuación\(\sin(x) = 0.6\), entonces\[\sin(-a) = -\sin(a) = -0.6\]

y así,\(x = -a\) es una solución de la ecuación\(\sin(x) = -0.6\). Para la ecuación\(\sin(x) = 0.6\), comenzamos por “aplicar la función sinusoidal inversa” a ambos lados de la ecuación.

\[\sin(x) = 0.6\]\[\sin^{-1}(\sin(x)) = \sin^{-1}(0.6)\]\[x = \sin^{-1}(0.6)\]

Debemos recordar que esta es sólo una solución de la ecuación. Ya que sabemos que la función sinusoidal es positiva en el primer y segundo cuadrantes, esta solución está en el primer cuadrante y hay otra solución en el segundo cuadrante. Usando\(x = \sin^{-1}(0.6)\) como arco de referencia (ángulo), la solución en el segundo cuadrante es\(x = \pi - \sin^{-1}(0.6)\). Ahora usamos el resultado de que si\(x = a\) es una solución de la ecuación\(\sin(x) = 0.6\), entonces\(x = -a\) es una solución de la ecuación\(\sin(x) = -0.6\). Tenga en cuenta que\[-(\pi - \sin^{-1}(0.6)) = -\pi + \sin^{-1}(0.6)\]

Nuestro trabajo hasta el momento se resume en la siguiente tabla.

Soluciones para\(\sin(x) = 0.6\)\([0, \pi]\)	Soluciones para\(\sin(x) = -0.6\)\([-\pi, 0]\)
\(x = \sin^{-1}(0.6)\)	\(x = -\sin^{-1}(0.6)\)
\(x = \pi - \sin^{-1}(0.6)\)	\(x = -\pi + \sin^{-1}(0.6)\)

En este punto, debemos usar una calculadora para verificar que los dos valores en la columna derecha son en realidad soluciones de la ecuación\(\sin(x) = -0.6\). Ahora que tenemos las soluciones para\(\sin(x) = -0.6\) en un ciclo completo, podemos usar el hecho de que el periodo de la función sinusoidal es\(2\pi\) y decir que las soluciones de la ecuación\(\sin(x) = -0.6\) tienen la forma

\[x = -\sin^{-1}(0.6) + k(2\pi) \space or \space x = (-\pi + \sin^{-1}(0.6)) + k(2\pi) \nonumber\]

donde\(k\) es algún número entero.

Ejercicio\(\PageIndex{3}\)

Determinar todas las soluciones de la ecuación\(2\sin(x) + 1.2 = 2.5\) en el intervalo\([-\pi, \pi]\) Luego usa la propiedad periódica de la función sinusoidal para escribir fórmulas que puedan ser utilizadas para generar todas las soluciones de esta ecuación.

Pista: Primero usa álgebra para reescribir la ecuación en la forma\(sin(x)\) = “algún número”.

Responder

Primero usamos álgebra para reescribir la ecuación\(2\sin(x) + 1.2 = 2.5\) en la forma

\[\sin(x) = 0.65\]

Entonces en el intervalo\([-\pi, \pi]\), las soluciones son\(x_{1} = \arcsin(0.65)\) y\(x_{2} = \pi - \arcsin(0.65)\). Entonces cualquier solución de la ecuación\(2\sin(x) + 1.2 = 2.5\) es de la forma

\[x = \arcsin(0.65) + k(2\pi)\]o\[x = \pi - \arcsin(0.65) + k(2\pi)\]

Resolviendo ecuaciones trigonométricas más complicadas

Ahora hemos aprendido a resolver ecuaciones de la forma\(\cos(x) = q\), y\(\sin(x) = q\), donde\(q\) está un número real y\(-1 \leq q \leq 1\). Podemos usar nuestra capacidad para resolver este tipo de ecuaciones para ayudar a resolver ecuaciones más complicadas de la forma\(\cos(f(x)) = q\), y\(\sin(f(x)) = q\) donde\(f\) hay alguna función. La idea (que es típica en matemáticas) es convertir este problema más complicado en dos problemas más simples. La idea es:

1. Hacer la sustitución\(t = f(x)\) para obtener una ecuación de la forma\(\cos(t) = q\), o\(\sin(t) = q\).
2. Resuelve la ecuación en (1) para\(t\).
3. Para cada solución\(t\) de la ecuación en (1), resolver la ecuación\(f(x) = t\) para\(x\). Este paso puede ser fácil, difícil o quizás imposible dependiendo de la ecuación\(f(x) = t\).

Este proceso se ilustrará en la próxima comprobación de progreso, que será una investigación guiada para resolver la ecuación\(3\cos(2x + 1) + 6 = 5\).

Ejercicio\(\PageIndex{4}\)

Vamos a resolver la ecuación\(3\cos(2x + 1) + 6 = 5\).

1. Primero, use álgebra para reescribir la ecuación en la forma\(\cos(2x + 1) = -\dfrac{1}{3}\). Después, hacer la sustitución\(t = 2x + 1\).
2. Determinar todas las soluciones de la ecuación\(\cos(t) = -\dfrac{1}{3}\) con\(-\pi \leq t \leq \pi\).
3. Para cada una de estas dos soluciones, utilice\(t = 2x + 1\) para encontrar las soluciones correspondientes para\(x\). Además, utilizar la sustitución\(t = 2x + 1\) para escribir\(-\pi \leq 2x + 1 \leq \pi\) y resolver esta desigualdad para\(x\). Esto dará todas las soluciones de la ecuación\(\cos(2x + 1) = -\dfrac{1}{3}\) en un ciclo completo de la función dada por\(y = \cos(2x + 1)\)
4. Cuál es el periodo de la función\(y = \cos(2x + 1)\). Usa los resultados en (3) y este periodo para escribir fórmulas que generen todas las soluciones de la ecuación\(\cos(2x + 1) = -\dfrac{1}{3}\). Estas serán las soluciones de la ecuación original\(3\cos(2x + 1) + 6 = 5\).

Responder

1. \[3\cos(2x + 1) + 6 = 5\]\[3\cos(2x + 1) = -1\]\[\cos(2x + 1) = -\dfrac{1}{3}\]

2. \(t = \cos^{-1}(-\dfrac{1}{3})\)o\(t = -\cos^{-1}(-\dfrac{1}{3})\).

3. \[2x + 1 = \cos^{-1}(-\dfrac{1}{3})\]

\[2x = \cos^{-1}(-\dfrac{1}{3}) - 1\]

\[x = \dfrac{1}{2}\cos^{-1}(-\dfrac{1}{3}) - \dfrac{1}{2}\]

\[2x + 1 = -\cos^{-1}(-\dfrac{1}{3})\]

\[2x = -\cos^{-1}(-\dfrac{1}{3}) - 1\]

\[x = -\dfrac{1}{2}\cos^{-1}(-\dfrac{1}{3}) - \dfrac{1}{2}\]

4. El periodo de la función\(y = \cos(2x + 1)\). Por lo que se pueden utilizar las siguientes fórmulas para generar las soluciones para la ecuación.

\[x = (\dfrac{1}{2}\cos^{-1}(-\dfrac{1}{3}) - \dfrac{1}{2}) + k\pi\]o\[x = (-\dfrac{1}{2}\cos^{-1}(-\dfrac{1}{3}) - \dfrac{1}{2}) + k\pi\]

donde\(k\) es algún número entero. Observe que agregamos un múltiplo entero del periodo, que es\(\pi\), a las soluciones en (3).

Resolver ecuaciones que involucran la función tangente

Resolver una ecuación de la forma\(\tan(x) = q\) es muy similar a resolver ecuaciones de la forma\(\cos(x) = q\) o\(\sin(x) = q\). Las principales diferencias son que la función tangente tiene un periodo de\(\pi\) (en lugar de\(2\pi\)), y la ecuación\(\tan(x) = q\) tiene sólo una solución en un periodo completo. Nosotros, por supuesto, usamos la función tangente inversa para la ecuación\(\tan(x) = q\).

Ejercicio\(\PageIndex{5}\)

Utilice la función tangente inversa para determinar una solución de la ecuación\[4\tan(x) + 1 = 10\] en el intervalo\((-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2})\). Después determinar una fórmula que pueda ser utilizada para generar todas las soluciones de esta ecuación.

Responder

Primero escribimos la ecuación\(4\tan(x) + 1 = 10\) en la forma\(\tan(x) = \dfrac{9}{4}\). Entonces la única solución de la ecuación en el intervalo\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\) es

\[x = \arctan(\dfrac{9}{4})\]

Dado que el periodo de la función tangente es\(\pi\), cualquier solución de esta ecuación se puede escribir en la forma\[x = \arctan(\dfrac{9}{4}) + k\pi\] donde\(k\) es algún número entero.

Resumen

Una ecuación trigonométrica es una ecuación que involucra funciones trigonométricas. Si podemos escribir la ecuación trigonométrica en la forma “alguna función trigonométrica de\(x\)” = un número, entonces podemos usar la siguiente estrategia para resolver la ecuación.

• Encuentre una solución de la ecuación utilizando la función trigonométrica inversa apropiada.
• Determinar todas las soluciones de la ecuación dentro de un periodo completo de la función trigonométrica. (Esto a menudo implica el uso de un arco de referencia basado en la solución obtenida en el primer paso).
• Utilice el periodo de la función para escribir fórmulas para todas las soluciones de la ecuación trigonométrica.