2.E: Gráficas de las Funciones Trigonométricas (Ejercicios)

Ejercicio\(\PageIndex{1}\)

En cada una de las siguientes, la gráfica de la izquierda muestra el punto terminal de un arco\(t\) (con\(0 \leq t \leq 2\pi\)) en el círculo unitario. Las gráficas de la derecha muestran las gráficas de\(y = \cos(t)\) y\(y = \sin(t)\) con algunos puntos en la gráfica etiquetada. Coincidir con el punto en las gráficas de\(y = \cos(t)\) y\(y = \sin(t)\) que corresponden al punto en el círculo unitario. Además, indicar las coordenadas de los puntos sobre\(y = \cos(t)\) y\(y = \sin(t)\).

a)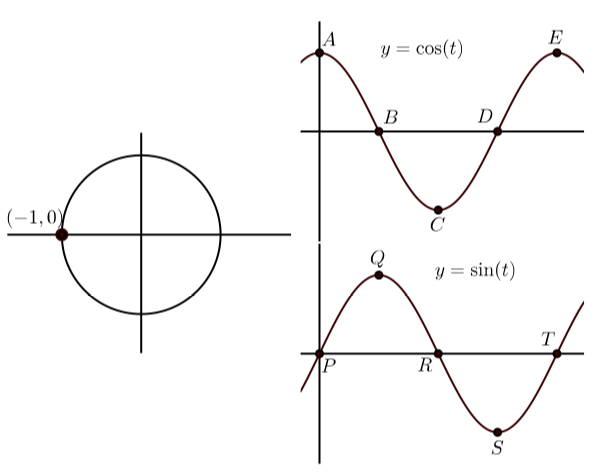

b)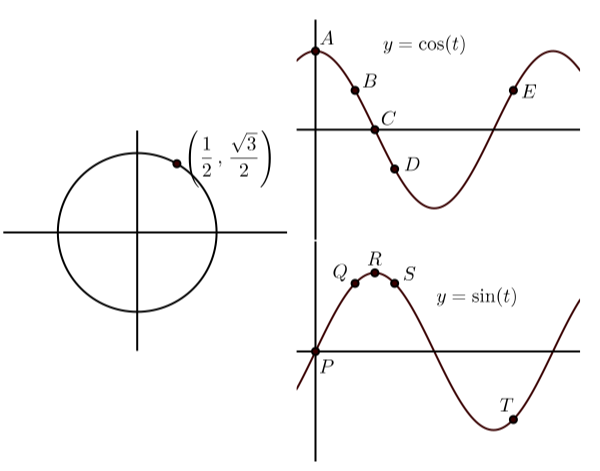

c)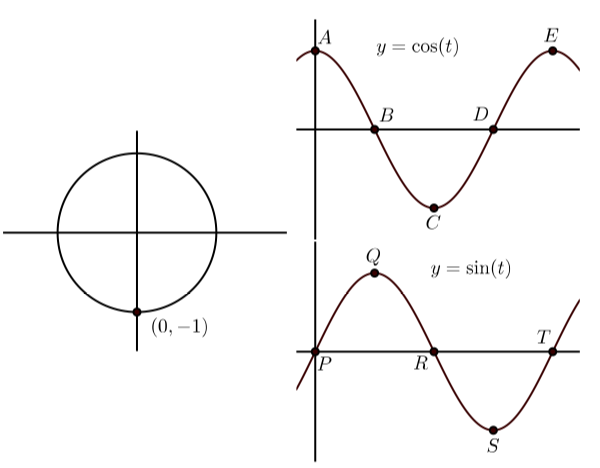

d)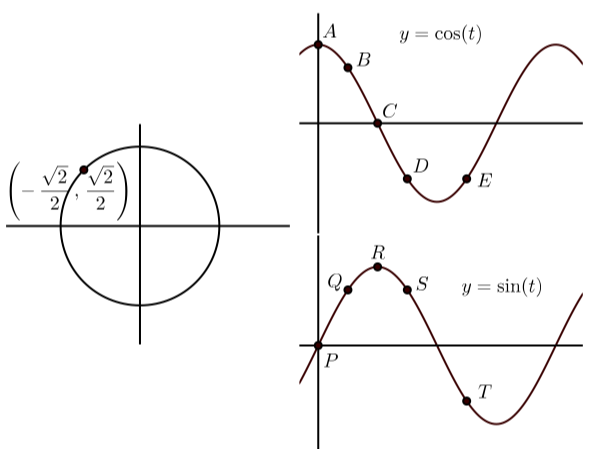

Responder

a)\(C(\pi, -1)\)\(R(\pi, 0)\)

b)\(B(\dfrac{\pi}{3}, \dfrac{1}{2})\)\(Q(\dfrac{\pi}{3}, \dfrac{\sqrt{3}}{2})\)

Ejercicio\(\PageIndex{2}\)

Para cada una de las siguientes, determine una ecuación de la forma\(y = A\cos(t)\) o\(y = A\sin(t)\) para la gráfica dada.

a)

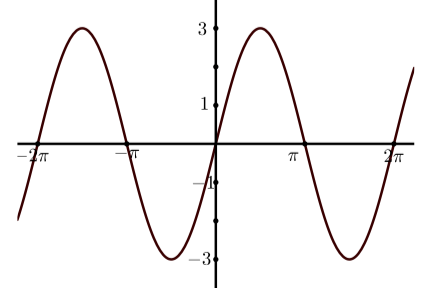
b)

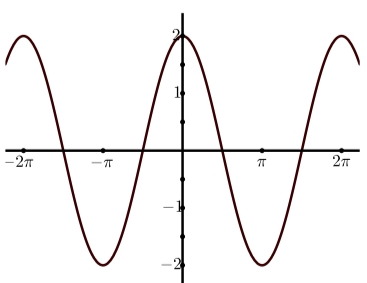
c)

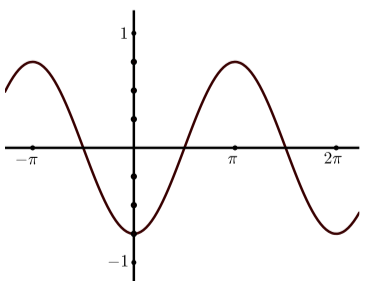
Responder

a)\(y = 3\sin(x)\)

b)\(y = 2\cos(x)\)

Ejercicio\(\PageIndex{3}\)

Dibuja la gráfica de cada una de las siguientes funciones sinusoidales en el intervalo indicado. Para cada gráfica,

• Declarar las\(t\) -intercepciones en el intervalo dado.
• Estado la\(y\) -intercepción.
• Indicar el valor máximo de la función y las coordenadas de todos los puntos donde se produce el valor máximo.
• Indicar el valor mínimo de la función y las coordenadas de todos los puntos donde se produce el valor mínimo.

1. \(y = \sin(t)\)con\(-2\pi \leq t \leq 2\pi\).
2. \(y = 3\cos(t)\)con\(-\pi \leq t \leq 3\pi\).
3. \(y = 5\sin(t)\)con\(0 \leq t\leq 4\pi\).
4. \(y = \dfrac{3}{7}\cos(t)\)con\(-\pi \leq t \leq 3\pi\).
5. \(y = -2.35\sin(t)\)con\(-\pi \leq t \leq \pi\).
6. \(y = -4\cos(t)\)con\(0 \leq t \leq 6\pi\).

Responder

(a)\(t\) -intercepta:\(-2\pi, -\pi, 0, \pi, 2\pi\),\(y\) -interceptar:\((0, 0)\)

El valor máximo es\(1\). El valor máximo se produce en los puntos\((-\dfrac{3\pi}{2}, 1)\) y\((\dfrac{\pi}{2}, 1)\).

El valor mínimo es\(-1\). El valor mínimo se produce en los puntos\((-\dfrac{\pi}{2}, -1)\) y\((\dfrac{3\pi}{2}, -1)\).

b)\(t\) -intercepta:\(-\dfrac{3\pi}{2}, -\dfrac{\pi}{2}, \dfrac{\pi}{2}, \dfrac{3\pi}{2}\),\(y\) -interceptar:\((0, 2)\)

El valor máximo es\(2\). El valor máximo se produce en los puntos\((0, 2)\) y\((2\pi, 2)\).

El valor mínimo es\(-2\). El valor mínimo se produce en los puntos\((-\pi -2)\),\((\pi, -2)\) y\((3\pi, -2)\).

Ejercicio\(\PageIndex{4}\)

A continuación se presenta una gráfica de poco más de un periodo de una función sinusoidal. Seis puntos están etiquetados en la gráfica.

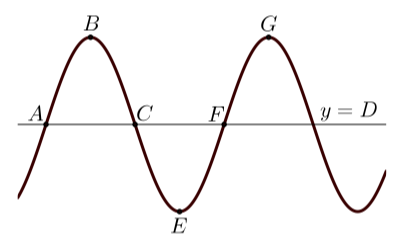
Figura\(\PageIndex{1}\)

Para cada una de las siguientes funciones sinusoidales:

• Anote la amplitud, el periodo, el desplazamiento de fase y el desplazamiento vertical.
• Anotar las coordenadas de los puntos\(A, B, C, E, F\), y\(G\). Dado que las funciones son periódicas, hay varias respuestas correctas. Para estas funciones, hacer que el punto\(A\) esté lo más cerca posible del origen.

Observe que la línea horizontal no es el eje horizontal sino más bien, la línea\(y = D\).

\[(a) y = 2\sin(\pi x)\]

\[(b) y = 7.2\cos(2x)\]

\[(c) y = 3\sin(x - \dfrac{\pi}{4})\]

\[(d) y = 3\sin(x + \dfrac{\pi}{4})\]

\[(e) y = 4\cos(x - \dfrac{\pi}{3})\]

\[(f) y = 2.8\cos(2(x - \dfrac{\pi}{3}))\]

\[(g) y = 4\sin(2(x - \dfrac{\pi}{4}))+1\]

\[(h) y = -4\cos(2(x + \dfrac{\pi}{4}))+1\]

\[(i) y = 3\cos(2\pi x - \dfrac{\pi}{2})\]

\[(j) y = -1.75\sin(2x - \dfrac{\pi}{3}) + 2\]

\[(k) y = 5\sin(120\pi x)\]

\[(l) y = 40\sin(50\pi(x - \dfrac{1}{100}))\]

Responder

a)\(y = 2\sin(\pi x)\). La amplitud es\(2\); el periodo es\(2\); el desplazamiento de fase es\(0\); y el desplazamiento vertical es\(0\).

\[A(0, 0)\]\[B(\dfrac{\pi}{2}, 2)\]\[C(\pi, 0)\]\[E(\dfrac{3\pi}{2}, -2)\]\[F(2\pi, 0)\]\[G(\dfrac{5\pi}{2}, 2)\]

c)\(y = 3\sin(x - \dfrac{\pi}{4})\). La amplitud es\(3\); el periodo es\(2\pi\); el desplazamiento de fase es\(\dfrac{\pi}{4}\); y el desplazamiento vertical es\(0\).

\[A(\dfrac{\pi}{4}, 0)\]\[B(\dfrac{3\pi}{4}, 3)\]\[C(\dfrac{5\pi}{4}, 0)\]\[E(\dfrac{7\pi}{4}, -3)\]\[F(\dfrac{7\pi}{4}, -3)\]\[G(\dfrac{11\pi}{4}, 3)\]

g)\(y = 4\sin(2(x - \dfrac{\pi}{4})) + 1\). La amplitud es\(4\); el periodo es\(\pi\); el desplazamiento de fase es\(\dfrac{\pi}{4}\); y el desplazamiento vertical es\(1\).

\[A(\dfrac{\pi}{4}, 1)\]\[B(\dfrac{\pi}{2}, 5)\]\[C(\dfrac{3\pi}{4}, 1)\]\[E(\pi, -3)\]\[F(\dfrac{5\pi}{4}, 1)\]\[G(\dfrac{3\pi}{2}, 5)\]

Ejercicio\(\PageIndex{5}\)

Cada una de las siguientes gráficas es una gráfica de una función sinusoidal. En cada caso:

• Determinar la amplitud de la función sinusoidal.
• Determinar el periodo de la función sinusoidal.
• Determinar el desplazamiento vertical de la función sinusoidal.
• Determinar una ecuación de la forma\(y = A\sin(B(x - C)) + D\) que produce la gráfica dada.
• Determinar una ecuación de la forma\(y = A\cos(B(x - C)) + D\) que produce la gráfica dada.

a)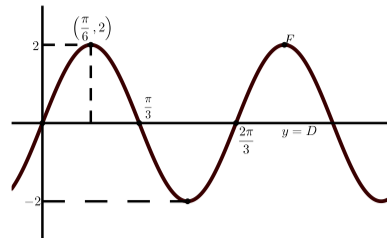

b)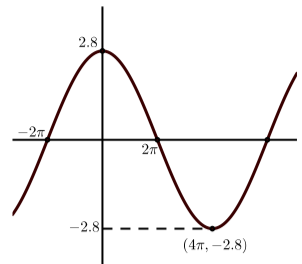

c)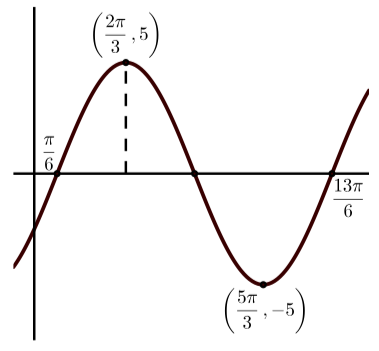

d)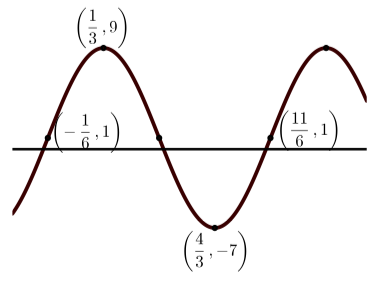

e)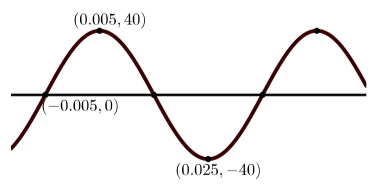

f)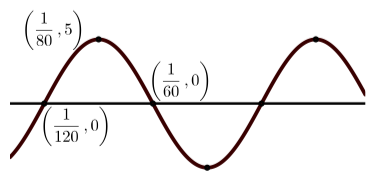

Responder

(a) La amplitud es\(2\); el periodo es\(\dfrac{2\pi}{3}\); y no hay desplazamiento vertical.

Porque\(y = A\sin(B(x - C)) + D\), no hay desplazamiento de fase y así\(C = 0\). Entonces\[y = 2\sin(3x)\]. Porque\(y = A\cos(B(x - C)) + D\), el desplazamiento de fase es\(\dfrac{\pi}{6}\) y así\(C = \dfrac{\pi}{6}\). Entonces\[y = 2\cos(3(x - \dfrac{\pi}{6}))\].

d) La amplitud es\(8\); el periodo es\(2\); y el desplazamiento vertical es\(1\).

Porque\(y = A\sin(B(x - C)) + D\), el desplazamiento de fase es\(-\dfrac{1}{6}\) y así\(C = -\dfrac{1}{6}\). Entonces\[y = 8\sin(\pi(x + \dfrac{1}{6}))\]. Porque\(y = A\cos(B(x - C)) + D\), el desplazamiento de fase es\(\dfrac{1}{3}\) y así\(C = \dfrac{1}{3}\). Entonces\[y = 8\cos(\pi(x - \dfrac{1}{3})) + 1\].

Ejercicio\(\PageIndex{6}\)

Cada uno de los siguientes enlaces web es a un applet en Geogebratube. Para cada uno se da la gráfica de una función sinusoidal. El objetivo es determinar una función de la forma

\[f(x) = A\sin(B(x - C)) + D\]o\[f(x) = A\cos(B(x - C)) + D\]
como se indica en el applet. Hay casillas que se deben usar para ingresar los valores de\(A, B, C\), y\(D\).

1. gvsu.edu/s/09f
2. gvsu.edu/s/09g
3. http://gvsu.edu/s/09h
4. gvsu.edu/s/09i
5. gvsu.edu/s/09j
6. http://gvsu.edu/s/09k

Ejercicio\(\PageIndex{7}\)

Determinar la amplitud, periodo, desplazamiento de fase y desplazamiento vertical para cada una de las siguientes sinusoides. Luego usa esta información para graficar un periodo completo de la sinusoide y las coordenadas de estado de un punto alto, un punto bajo y un punto donde la sinusoide cruza la línea central.

\[(a) y = 4\sin(\pi x - \dfrac{\pi}{8})\]

\[(b) y = 5\cos(4x + \dfrac{\pi}{2}) + 2\]

\[(c) y = -3.2\cos(50\pi x - \dfrac{\pi}{2})\]

\[(d) y = 4.8\sin(\dfrac{1}{4}x + \dfrac{\pi}{8})\]

Agrega texto aquí. Para que el número automático funcione, es necesario agregar la plantilla “AutoNum” (preferiblemente al final) a la página.

Responder

(a) Escribimos\(y = 4\sin(\pi x - \dfrac{\pi}{8}) = 4\sin(\pi(x - \dfrac{1}{8}))\). Entonces la amplitud es\(4\), el periodo es\(2\), el desplazamiento de fase es\(\dfrac{1}{8}\), y no hay desplazamiento vertical.

Algunos puntos altos en la gráfica:\((\dfrac{5}{8}, 4)\),\((\dfrac{21}{8}, 4)\). Algunos puntos bajos en la gráfica:\((\dfrac{13}{8}, -4)\),\((\dfrac{29}{8}, -4)\). La gráfica cruza la línea central en:\((\dfrac{1}{8}, 0)\),\((\dfrac{9}{8}, 0)\),\((\dfrac{17}{8}, 0)\).

(b) Escribimos\(y = 4\cos(4x + \dfrac{\pi}{2}) + 2 = 5\cos(4(x + \dfrac{\pi}{8})) + 2\). Entonces la amplitud es\(5\), el periodo es\(\dfrac{\pi}{2}\), el desplazamiento de fase es\(-\dfrac{\pi}{8}\), y el desplazamiento vertical lo es\(2\).

Algunos puntos altos en la gráfica:\((-\dfrac{\pi}{8}, 7)\),\((\dfrac{3\pi}{8}, 7)\). Algunos puntos bajos en la gráfica:\((\dfrac{\pi}{8}, -3)\),\((\dfrac{5\pi}{8}, -3)\). La gráfica cruza la línea central en:\((0, 2)\),\((\dfrac{\pi}{4}, 2)\),\((\dfrac{\pi}{2}, 2)\).

Ejercicio\(\PageIndex{8}\)

Modelando un Latido. Para una persona determinada en reposo, supongamos que el corazón bombea sangre a un ritmo regular de aproximadamente 75 pulsos por minuto. Además, supongamos que el volumen del corazón de esta persona es aproximadamente de 150 mililitros (ml), y empuja hacia fuera alrededor de\(54\%\) su volumen con cada latido. Modelaremos el volumen,\(V(t)\) de sangre (en mililitros) en el corazón en cualquier momento\(t\), como una función sinusoidal de la forma\[V(t) = A\cos(Bt) + D\]

1. Si elegimos tiempo\(0\) para ser un momento en el que el corazón está lleno de sangre, ¿por qué es razonable usar una función coseno para nuestro modelo?
2. ¿Cuál es el valor máximo de\(V(t)\)? ¿Cuál es el valor mínimo de (V (t)\)? ¿Qué nos dice esto sobre los valores de A y D? Explique.
3. La frecuencia de un movimiento armónico simple es el número de periodos por unidad de tiempo, o el número de pulsos por minuto en este ejemplo. ¿Cómo se relaciona la frecuencia f con el periodo? ¿Qué valor debe tener B? Explique.
4. Dibuja una gráfica (sin calculadora) de tu (V (t)\) usando tus valores de A, B y D, de dos periodos comenzando en\(t = 0\).
5. Identificar claramente los valores máximos y mínimos de\(V(t)\) en la gráfica. ¿Qué nos dicen estos números del corazón en estos momentos?

Responder

b) El valor máximo es\(150\) ml, y el valor mínimo es\(81\) ml. Para que podamos usar\(A = \dfrac{150 - 81}{2} = 34.5\) y\(D = \dfrac{150 + 81}{2} = 115.5\).

(c) El periodo es\(\dfrac{1}{75}\) min.

Ejercicio\(\PageIndex{9}\)

La electricidad que se suministra a las casas residenciales se denomina corriente alterna (CA) porque la corriente varía sinusoidalmente con el tiempo. El voltaje que hace que la corriente fluya también varía sinusoidalmente con el tiempo. En un circuito de corriente alterna (CA), el voltaje\(V\) (en voltios) en función del tiempo es una función sinusoidal de la forma\[V = V_{0}\sin(2\pi ft)\]

donde\(V_{0}\) es una constante positiva y f es la frecuencia. La frecuencia es el número de oscilaciones completas (ciclos) por segundo. En Estados Unidos, fis 60 hertz (Hz), lo que significa que la frecuencia es de 60 ciclos por segundo.

1. ¿Cuál es la amplitud y cuál es el periodo de la función sinusoidal en (1)? La potencia (en vatios) entregada a una resistencia R (en ohmios) en cualquier momento t viene dada por\[P = \dfrac{V^2}{R}\]
2. Demostrar que\(P = \dfrac{V^2}{R}\sin^2(2\pi ft)\)
3. A continuación se muestra la gráfica de\(P\) como función del tiempo.

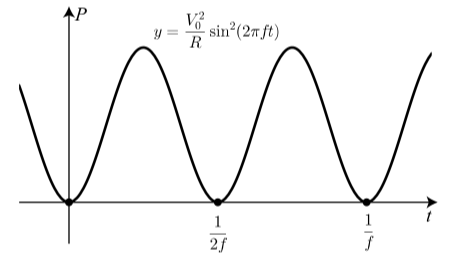
Figura\(\PageIndex{2}\)

Suponiendo que esto demuestra que\(P\) es una función sinusoidal de t, escriba\(P\) como una función sinusoidal del tiempo\(t\) usando el negativo de una función coseno sin desplazamiento de fase.
4. Entonces sabemos eso\(P = \dfrac{V_{0}^2}{R}\sin^2(2\pi ft)\) y que P es igual a la función sinusoidal en la parte (c). Establezca las dos expresiones\(P\) iguales entre sí y use la ecuación resultante para concluir que\[sin^2(2\pi ft) = \dfrac{1}{2}[1 - cos(4\pi ft)]\]

Ejercicio\(\PageIndex{10}\)

La electricidad que se suministra a las casas residenciales se denomina corriente alterna (CA) porque la corriente varía sinusoidalmente con el tiempo. El voltaje que hace que la corriente fluya también varía sinusoidalmente con el tiempo. Tanto la corriente como la tensión tienen una frecuencia de 60 ciclos por segundo, pero tienen diferentes desplazamientos de fase. (Nota: Una frecuencia de 60 ciclos por segundo corresponde a un periodo\(\dfrac{1}{60}\) de un segundo.)

Dejar\(C\) ser la corriente (en amperios), dejar\(V\) ser el voltaje (en voltios), y dejar t ser el tiempo (en segundos). La siguiente lista da información que se conoce sobre\(C\) y\(V\).

• La corriente\(C\) es una función sinusoidal del tiempo con una frecuencia de 60 ciclos por segundo, y alcanza su máximo de 5 amperios cuando\(t = 0\) segundos.
• El voltaje\(V\) es una función sinusoidal del tiempo con una frecuencia de 60 ciclos por segundo. Como se muestra en las gráficas de la página siguiente,\(V\) “lidera” la corriente en el sentido de que alcanza su máximo antes de que la corriente alcance su máximo. (“Líder” corresponde a un desplazamiento de fase negativo, y “rezagado” corresponde a un desplazamiento de fase positivo). En este caso, el voltaje V conduce la corriente por 0.003 segundos, lo que significa que alcanza su máximo 0.003 segundos antes de que la corriente alcance su máximo.
• El voltaje pico es de 180 voltios.
• No hay desplazamiento vertical ni en el gráfico de corriente ni en el gráfico de voltaje.

1. Determinar las funciones sinusoidales para ambos\(C\) y\(V\).
2. ¿Cuál es el voltaje cuando la corriente es máxima?
3. ¿Cuál es la corriente cuando el voltaje es mínimo?
4. ¿Cuál es la corriente cuando el voltaje es igual a cero?

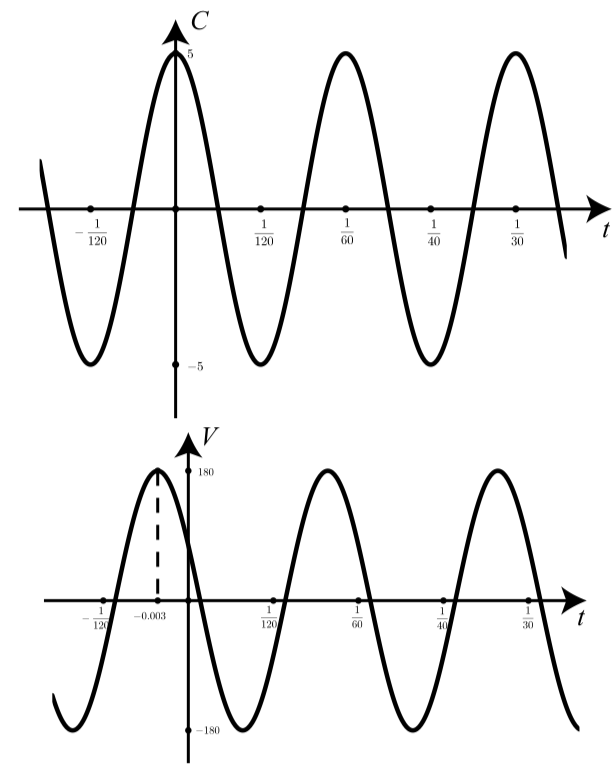
Figura\(\PageIndex{3}\): Corriente\(C\) y voltaje\(V\) como funciones del tiempo

Ejercicio\(\PageIndex{11}\)

Dejaremos\(t\) ser el número del día del año. En la siguiente tabla se muestran las horas de salida del sol (en minutos desde la medianoche) de ciertos días del año en Houghton, Michigan.

día	1	31	61	91	121	151	181	211	241	271	301	331	361
tiempo	521	501	453	394	339	304	302	330	369	408	451	494	520

Los puntos para esta tabla se trazan en la siguiente gráfica.

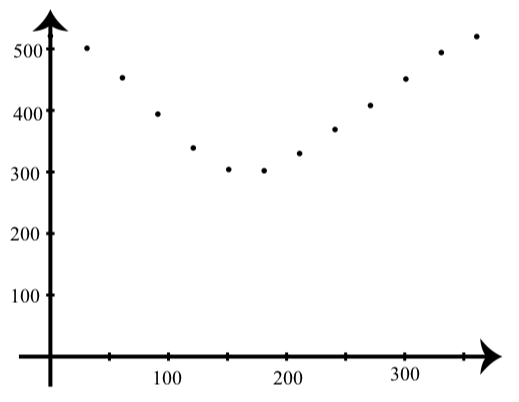
Figura\(\PageIndex{4}\)

1. \(t\)Sea el número del día del año y deje\(y\) ser la hora del amanecer en minutos desde la medianoche en Houghton, MI. Determinar un modelo sinusoidal para\(y\) como una función de\(t\).
2. Para verificar el trabajo en la Parte (a), utilice una utilidad gráfica o Geogebra para trazar los puntos en la tabla y superponer la gráfica de la función de la Parte (a).
3. Utilice Geogebra para determinar un modelo sinusoidal para\(y\) como una función de\(t\). Este modelo estará en la forma\(y = a\sin(bt + c) + d\), dónde\(a, b, c\), y\(d\) son números reales.
4. Determinar la amplitud, periodo, desplazamiento de fase y desplazamiento vertical para el modelo sinusoidal en la Parte (c).

Ejercicio\(\PageIndex{12}\)

Modelando la Distancia de la Tierra al Sol.

La órbita de la Tierra alrededor del sol no es un círculo perfecto. En 1609 Johannes Kepler publicó dos de sus famosas leyes del movimiento planetario, una de las cuales establece que las órbitas planetarias son en realidad elipses. Por lo que la distancia de la Tierra al sol no es una constante, sino que varía a lo largo de su órbita (asumiremos un año de 365 días). Según las Efemérides estadounidenses de 1996, las distancias del sol a la Tierra el día 21 de cada mes se dan en la Tabla 2.3. Las distancias se miden en Unidades Astronómicas (AU), donde 1 AU es aproximadamente\(149597900\) kilómetros.

http://image.gsfc.nasa.gov/poetry/venus/q638.html

Mes	Día del año	Distancia
enero	21	0.9840
febrero	52	0.9888
marzo	80	0.9962
abril	111	1.0050
Mayo	141	1.0122
junio	172	1.0163
julio	202	1.0161
agosto	233	1.0116
septiembre	264	1.0039
Octubre	294	0.9954
noviembre	325	0.9878
diciembre	355	0.9837

Tabla\(\PageIndex{1}\): Distancias de la Tierra al Sol el 21 de cada mes

En la Figura se da una gráfica de estos datos con el día del año a lo largo del eje horizontal y la distancia desde la Tierra hasta el sol en el eje vertical\(\PageIndex{5}\).

Utilizaremos una función sinusoidal para modelar estos datos. Es decir, dejaremos\(f(t)\) ser la distancia de la Tierra al Sol el día\(t\) del año y que\[f(t) = A\sin(B(t - C)) + D\]

1. ¿Cuáles son las distancias máxima y mínima de la Tierra al Sol dadas por los datos? ¿Qué nos dice esto sobre la amplitud off.t/? Usa esto para aproximar los valores de\(A\) y\(D\) en la función modelo\(f\)? ¿Cuál es la línea central para este modelo sinusoidal?
2. El periodo de esta función sinusoidal es de 365 días. ¿Cuál es el valor\(B\) de esta función sinusoidal?
3. Dibuja la línea central que encontraste en la parte (a) en la gráfica de los datos de la Figura\(\PageIndex{5}\). ¿A aproximadamente qué valor de la gráfica de\(t\) fintersectará esta línea central? ¿Cómo se relaciona este número con el desplazamiento de fase de los datos? ¿Cuál es el valor\(C\) de esta función sinusoidal?
4. Usa Geogebra para trazar los puntos a partir de los datos en Tabla\(\PageIndex{1}\) y luego usa Geogebra para dibujar la gráfica del modelo sinusoidal\(f(t) = A\sin(B(t - C)) + D\). ¿Esta función modela razonablemente bien los datos?
5. Utilice el modelo sinusoidal\(f(t) = A\sin(B(t - C)) + D\) para estimar la distancia de la Tierra al Sol el 4 de julio.

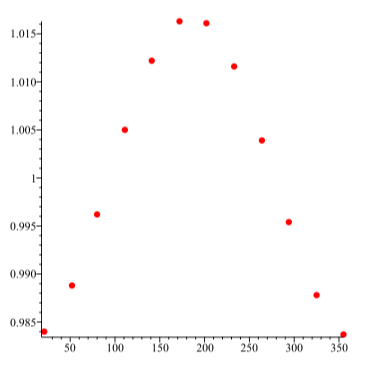
Figura\(\PageIndex{5}\): Distancia de la Tierra al Sol en función del día del año

Ejercicio\(\PageIndex{13}\)

Continuación de Ejercicio\(\PageIndex{12}\).

Utilice Geogebra para trazar los puntos a partir de los datos en la Tabla\(\PageIndex{1}\). Luego usa el comando “FitSin” en Geogebra para encontrar un modelo sinusoidal para estos datos de la forma\(g(t) = a\sin(bt + c) + d\)

¿Cuál es la amplitud de este modelo sinusoidal? ¿Cuál es el periodo? ¿Cuál es el cambio horizontal? ¿Cuál es el cambio de fase?

¿Cómo se comparan estos valores con los valores correspondientes para la sinusoide\(f(t) = A\sin(B(t - C)) + D\) obtenidos en el Ejercicio (6)?

Ejercicio\(\PageIndex{14}\)

A medida que la luna orbita la tierra, la apariencia de la luna cambia. Vemos varios discos lunares en distintas épocas del mes. Estos cambios reaparecen durante cada mes lunar. No obstante, un mes lunar no es exactamente lo mismo que los doce meses que hoy usamos en nuestro calendario. Un mes lunar es el número de días que tarda la luna en pasar por un ciclo completo desde una luna llena (100% de iluminación) hasta la siguiente luna llena.

Los siguientes datos fueron recopilados del sitio web del Observatorio Naval de Estados Unidos. Los datos son el porcentaje de la luna que se ilumina es valor geocéntrico del porcentaje de la luna que se ilumina. Es decir, el porcentaje de iluminación se calcula para un observador ficticio ubicado en el centro de la Tierra.

Fecha	Porcentaje Iluminado
3/1/2013	\(87\%\)
3/3/2013	\(69\%\)
3/5/2017	\(47\%\)
3/7/2017	\(25\%\)
3/9/2017	\(9\%\)
3/12/2013	\(0\%\)
13/03/2013	\(2\%\)
15/03/2017	\(12\%\)
17/03/2013	\(27\%\)
19/03/2013	\(45\%\)
21/3/2013	\(64\%\)
23/3/2013	\(81\%\)
25/03/2013	\(94\%\)
27/03/2013	\(100\%\)
29/03/2013	\(96\%\)

Mesa\(\PageIndex{2}\)

1. Determinar una función sinusoidal de la forma\(y = A\cos(B(t - C)) + D\) para modelar estos datos. Para esta función, que x sea el número de días desde principios de marzo de 2017 y que y sea el porcentaje de la luna que se ilumina. ¿Cuál es la amplitud, periodo, desplazamiento de fase y desplazamiento vertical de esta función sinusoidal?
2. Usa Geogebra para dibujar una gráfica de dispersión de estos datos y superponer la gráfica de la función de la parte (a).
3. Utilice Geogebra para determinar una función sinusoidal de la forma\(y = A\sin(Bx + K) + D\) para modelar estos datos y superponer su gráfica en la gráfica de dispersión. ¿Cuál es la amplitud, periodo, desplazamiento de fase y desplazamiento vertical de esta función sinusoidal?

Ejercicio\(\PageIndex{15}\)

Cada uno de los siguientes enlaces web es a un applet en Geogebratube. Para cada uno, se trazan los datos y en algunos casos, los datos reales se muestran en una hoja de distribución a la derecha. El objetivo es determinar una función de la forma

\[f(x) = A\sin(B(x- C)) + D\]o\[f(x) = A\cos(B(x- C)) + D\]

que se ajuste a los datos lo más cerca posible. Cada applet indicará qué tipo de función usar. Hay casillas que se deben usar para ingresar los valores de\(A, B, C\), y\(D\).

1. gvsu.edu/s/09l
2. http://gvsu.edu/s/09m
3. http://gvsu.edu/s/09n
4. http://gvsu.edu/s/09o

Ejercicio\(\PageIndex{16}\)

En este ejercicio, exploraremos el periodo de la función tangente.

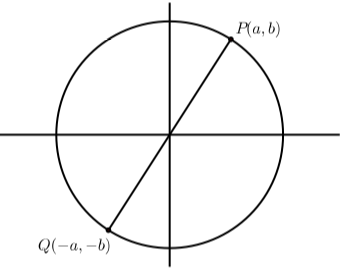
Figura\(\PageIndex{6}\)

1. Utilizar la definición de la función tangente y el hecho de que el periodo tanto de las funciones seno como coseno es igual\(2\pi\) a para probar que para cualquier número real t en el dominio de la función tangente,\[\tan(t + 2\pi) = \tan(t)\] Sin embargo, esto no prueba que el periodo de la función tangente sea igual a\(2\pi\). Ahora vamos a demostrar que el periodo es igual a\(\pi\). La clave de la prueba es el diagrama de la derecha. Supongamos que\(P\) es el punto terminal del arco\(t\). Entonces\(\cos(t) = a\) y\(\sin(t) = b\). El diagrama muestra un punto Q que es el punto terminal del arco\(t + \pi\). Por la simetría del círculo, sabemos que el punto\(Q\) tiene coordenadas\((-a, -b)\).
2. Explique por qué\(\cos(t + \pi) = -a\) y\(\sin(t + \pi) = -b\)
3. Utilice la información en la parte (1) y la definición de la función tangente para demostrarlo\(\tan(t + \pi) = \tan(t)\).

El diagrama también indica que el valor positivo más pequeño de\(p\) para el cual\(\tan(t + p) = \tan(t)\) debe ser\(p = \pi\). De ahí que el periodo al que sea igual la función tangente\(\pi\).

Ejercicio\(\PageIndex{17}\)

Eso lo hemos visto\(\cos(-t) = \cos(t)\) y\(\sin(-t) = \sin(t)\) por cada número real\(t\). Ahora supongamos que\(t\) es un número real para el que\(\tan(t)\) se define.

1. Utilice la definición de la función tangente para escribir una fórmula para\(\tan(-t)\) en términos de\(\sin(-t)\) y\(\cos(-t)\).
2. Ahora usa las identidades de arco negativo para las funciones coseno y seno para ayudar a probarlo\(\tan(-t) = -\tan(t)\). Esto se llama la identidad de arco negativo para la función tangente.
3. Utilice la identidad de arco negativo para la función tangente para explicar por qué la gráfica de\(y = \tan(t)\) es simétrica sobre el origen.

Ejercicio\(\PageIndex{18}\)

Utilice las identidades de arco negativo para seno, coseno y tangente para ayudar a probar las siguientes identidades de arco negativo para cosecante, secante y cotangente.

1. Por cada número real\(t\) para el cual\(t \neq k\pi\) para cada entero\(k\),\(\csc(-t) = -\csc(t)\).
2. Por cada número real\(t\) para el cual\(t \neq \dfrac{\pi}{2} + k\pi\) para cada entero\(k\),\(\sec(-t) = \sec(t)\).
3. Por cada número real\(t\) para el cual\(t \neq k\pi\) para cada entero\(k\),\(\cot(-t) = -\cot(t)\).

Ejercicio\(\PageIndex{19}\)

La Función Cosecante.

En caso necesario, remitirse a la Sección 1.6 para responder a las siguientes preguntas.

1. ¿Cómo se define la función cosecante?
2. ¿Cuál es el dominio de la función cosecante?
3. ¿Dónde tendrá asíntotas verticales la gráfica de la función cosecante?
4. ¿Cuál es el periodo de la función cosecante?

Ejercicio\(\PageIndex{20}\)

Explorando la Gráfica de la Función Cosecante.

1. Utilice el Applet de Geogebra con la siguiente dirección web para explorar la relación entre la gráfica de la función cosecante y la función seno. http://gvsu.edu/s/0bH En el applet,\(y = \sin(t)\) se muestra la gráfica de y se deja fija. Los puntos en la gráfica de\(y = \csc(t)\) se generan mediante el uso del control deslizante para\(t\). Para cada valor de\(t\), se dibuja una línea vertical del punto\((t, \sin(t))\) al punto\((t, \csc(t))\). Observe cómo estos puntos indican que la gráfica de la función cosecante tiene asíntotas verticales en\(t = 0, t = \pi\) y\(t = 2\pi\).
2. Utilice una utilidad gráfica para dibujar la gráfica de\(y = \csc(t)\) usar\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\) y\(-10 \leq y \leq 10\). Nota: Puede ser necesario usar\(\csc(x) = \dfrac{1}{\sin(x)}\)
3. Utilice una utilidad gráfica para dibujar la gráfica de\(y = \csc(t)\) usar\(-\dfrac{3\pi}{2} \leq x \leq \dfrac{3\pi}{2}\) y\(-10 \leq y \leq 10\).

Ejercicio\(\PageIndex{21}\)

La Gráfica de la Función Cosecante.

1. ¿Por qué la gráfica de\(y = \csc(t)\) tiene asíntotas verticales en\(x = 0, x = \pi\), y\(x = 2\pi\)? ¿Cuál es el dominio de la función cosecante?
2. ¿Por qué es la gráfica de\(y = \csc(t)\) arriba del eje x cuándo\(0 < x < \pi\)?
3. ¿Por qué es la gráfica de\(y = \csc(t)\) arriba del eje x cuándo\(\pi < x < 2\pi\)?
4. ¿Cuál es el rango de la función cosecante?

Ejercicio\(\PageIndex{22}\)

La función cotangente.

En caso necesario, remitirse a la Sección 1.6 para responder a las siguientes preguntas.

1. ¿Cómo se define la función cotangente?
2. ¿Cuál es el dominio de la función cotangente?
3. ¿Dónde tendrá asíntotas verticales la gráfica de la función cotangente?
4. ¿Cuál es el periodo de la función cotangente?

Ejercicio\(\PageIndex{23}\)

Explorando la Gráfica de la Función Cotangente.

1. Utilice una utilidad gráfica para dibujar la gráfica de\(y = \cot(x)\) usar\(-\pi \leq x \leq \pi\) y\(-10 \leq y \leq 10\). Nota: Puede ser necesario su uso\(\cot(x) = \dfrac{1}{tan(x)}\).
2. Utilice una utilidad gráfica para dibujar la gráfica de\(y = \cot(x)\) usar\(-2\pi \leq x \leq 2\pi\) y\(-10 \leq y \leq 10\).

Ejercicio\(\PageIndex{24}\)

La Gráfica de la Función Cotangente.

1. ¿Por qué la gráfica de\(y = \cot(t)\) tiene asíntotas verticales en\(x = 0, x = \pi\), y\(x = 2\pi\)? ¿Cuál es el dominio de la función cosecante?
2. ¿Por qué es la gráfica de\(y = \cot(t)\) arriba del eje x cuándo\(0 < x < \dfrac{\pi}{2}\) y cuándo\(\pi < x < \dfrac{3\pi}{2}\)?
3. ¿Por qué es la gráfica de\(y = \cot(t)\) arriba del eje x cuándo\(\dfrac{\pi}{2} < x < \pi\) y cuándo\(\dfrac{3\pi}{2} < x < 2\pi\)?
4. ¿Cuál es el rango de la función cotangente?

Ejercicio\(\PageIndex{25}\)

Reescribir cada uno de los siguientes usando la función trigonométrica correspondiente para la función trigonométrica inversa. Luego determinar el valor exacto de la función trigonométrica inversa.

\[(a) t = \arcsin(\dfrac{\sqrt{2}}{2})\]

\[(b) t = \arcsin(-\dfrac{\sqrt{2}}{2})\]

\[(c) t = \arccos(\dfrac{\sqrt{2}}{2})\]

\[(d) t = \arccos(-\dfrac{\sqrt{2}}{2})\]

\[(e) y = \tan^{-1}(\dfrac{\sqrt{3}}{2})\]

\[(f) y = \tan^{-1}(\dfrac{-\sqrt{3}}{2})\]

\[(g) y = \cos^{-1}(0)\]

\[(h) t = \arctan(0)\]

\[(i) y = \sin^{-1}(-\dfrac{1}{2})\]

\[(j) y = \cos^{-1}(-\dfrac{1}{2})\]

Responder

(a)\(t = \arcsin(\dfrac{\sqrt{2}}{2})\) medios\(\sin(t) = \dfrac{\sqrt{2}}{2}\) y\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\). Ya que\(\sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}\), vemos eso\(t = \arcsin(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}\).

(b)\(t = \arcsin(-\dfrac{\sqrt{2}}{2})\) medios\(\sin(t) = -\dfrac{\sqrt{2}}{2}\) y\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\). Ya que\(\sin(\dfrac{-\pi}{4}) = -\dfrac{\sqrt{2}}{2}\), vemos eso\(t = \arcsin(\dfrac{\sqrt{2}}{2}) = -\dfrac{\pi}{4}\).

(d)\(t = \arccos(-\dfrac{\sqrt{2}}{2})\) medios\(\cos(t) = -\dfrac{\sqrt{2}}{2}\) y\(0 \leq t \leq \pi\). Ya que\(\cos(\dfrac{3\pi}{4}) = -\dfrac{\sqrt{2}}{2}\), vemos eso\(t = \arccos(\dfrac{\sqrt{2}}{2}) = \dfrac{3\pi}{4}\).

(f)\(y = \tan^{-1}(-\dfrac{\sqrt{3}}{3})\) medios\(\tan(y) = -\dfrac{\sqrt{3}}{3}\) y\(-\dfrac{\pi}{2} < y < \dfrac{\pi}{2}\). Ya que\(\tan(-\dfrac{\pi}{6}) = -\dfrac{\sqrt{3}}{3}\), vemos eso\(y = \tan^{-1}(-\dfrac{\sqrt{3}}{2}) = -\dfrac{\pi}{6}\).

h)\(t = \arctan(0) = 0\)

j)\(y = \cos^{-1}(-\dfrac{1}{2}) = \dfrac{2\pi}{3}\).

Ejercicio\(\PageIndex{26}\)

Determinar el valor exacto de cada una de las siguientes expresiones.

\[(a) \sin(\sin^{-1}(1))\]

\[(b) \sin^{-1}(\sin(\dfrac{\pi}{3}))\]

\[(c) \cos^{-1}(\sin(\dfrac{\pi}{3}))\]

\[(d) \sin^{-1}(\sin(-\dfrac{\pi}{3}))\]

\[(e) \cos^{-1}(\cos(-\dfrac{\pi}{3}))\]

\[(f) \arcsin(\sin(\dfrac{2\pi}{3}))\]

\[(g) \tan(\arctan(1))\]

\[(h) \arctan(\tan(\dfrac{\pi}{4}))\]

\[(i) \arctan(\tan(\dfrac{3\pi}{4}))\]

Responder

a)\(\sin(\sin^{-1}(1)) = \sin(\dfrac{\pi}{2}) = 1\)

b)\(\sin^{-1}(\sin(\dfrac{\pi}{3})) = \sin^{-1}(\dfrac{\sqrt{3}}{2}) = \dfrac{\pi}{3}\)

e)\(\cos^{-1}(\cos(-\dfrac{\pi}{3})) = \cos^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{3}\)

f)\(\arcsin(\sin(\dfrac{2\pi}{3})) = \arcsin(\dfrac{\sqrt{3}}{2}) = \dfrac{\pi}{3}\)

i)\(\arctan(\tan(\dfrac{3\pi}{4})) = \arctan(-1) = -\dfrac{\pi}{4}\)

Ejercicio\(\PageIndex{27}\)

Determinar el valor exacto de cada una de las siguientes expresiones.

\[(a) \cos(\arcsin(\dfrac{2}{5}))\]

\[(b) \sin(\arccos(-\dfrac{2}{3}))\]

\[(c) \tan(\arcsin(\dfrac{1}{3}))\]

\[(d) \cos(\arcsin(-\dfrac{2}{5}))\]

\[(e) \tan(\arccos(-\dfrac{2}{9}))\]

Responder

(a) Dejar\(t = \arcsin(\dfrac{2}{5})\). Entonces\(\sin(t) = \dfrac{2}{5}\) y\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\), y

\[\cos^{2}(t) + \sin^{2}(t) = 1\]

\[\cos^{2}(t) + \dfrac{4}{25} = 1\]

\[\cos^{2}(t) = \dfrac{21}{25}\]

Ya que\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\), eso lo sabemos\(\cos(t) \geq 0\). De ahí,\(\cos(t) = \dfrac{\sqrt{21}}{5}\) y\(\cos(\arcsin(\dfrac{2}{5})) = \dfrac{\sqrt{21}}{5}\).

b)\(\sin(\arccos(-\dfrac{2}{3})) = \dfrac{\sqrt{5}}{3}\).

c)\(\tan(\arcsin(\dfrac{1}{3})) = \dfrac{1}{\sqrt{8}}\).

Ejercicio\(\PageIndex{28}\)

Este ejercicio proporciona una justificación de las propiedades de la función coseno inverso en la página 150. Dejar\(t\) ser un número real en el intervalo cerrado\([0, \pi]\) y dejar que luego\[y = \cos(t).\] veamos eso\(-1 \leq y \leq 1\) y\[\cos^{-1}(y) = t\]

1. Utilice las ecuaciones para reescribir la expresión\(\cos^{-1}(\cos(t))\).
2. Utilice las ecuaciones para reescribir la expresión\(\cos(\cos^{-1}(y))\).

Ejercicio\(\PageIndex{29}\)

Este ejercicio proporciona una justificación de las propiedades de la función coseno inverso en la página 151. Let\(t\) be a real number in the open interval\((-\dfrac{\pi}{2}, \dfrac{\pi}{2})\) and let\[y = \tan(t).\] We then see that\(y\) is a real number and\[\tan^{-1}(y) = t\]

1. Utilice las ecuaciones para reescribir la expresión\(\tan^{-1}(\tan(t))\).
2. Utilice las ecuaciones para reescribir la expresión\(\tan(\tan^{-1}(y))\).

Ejercicio\(\PageIndex{30}\)

Para cada una de las siguientes ecuaciones, utilice una gráfica para aproximar las soluciones (a tres decimales) de la ecuación en el intervalo indicado. Luego use la propiedad periódica de la función trigonométrica para escribir fórmulas que puedan ser utilizadas para aproximar cualquier solución de la ecuación dada.

1. \(\sin(x) = 0.75\)con\(-\pi \leq x \leq \pi\)
2. \(\cos(x) = 0.75\)con\(-\pi \leq x \leq \pi\)
3. \(\tan(x) = 0.75\)con\((-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2})\)
4. \(\sin(x) = -0.75\)con\(-\pi \leq x \leq \pi\)
5. \(\cos(x) = -0.75\)con\(-\pi \leq x \leq \pi\)
6. \(\tan(x) = -0.75\)con\((-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2})\)

Responder

(a)\(x = 0.848 + k(2\pi)\) o\(x = 2.294 + k(2\pi)\), donde\(k\) es un entero.

d)\(x = -0.848 + k(2\pi)\) o\(x = -2.294 + k(2\pi)\), donde\(k\) es un número entero.

Ejercicio\(\PageIndex{31}\)

Para cada una de las ecuaciones en el Ejercicio (1), utilice una función trigonométrica inversa para escribir los valores exactos de todas las soluciones de la ecuación en el intervalo indicado. Luego use la propiedad periódica de la función trigonométrica para escribir fórmulas que puedan ser utilizadas para generar todas las soluciones de la ecuación dada.

Responder

(a)\(x = \sin^{-1}(0.75) + k(2\pi)\) o\(x = (\pi - \sin^{-1}(0.75)) + k(2\pi)\), donde\(k\) es un entero.

d)\(x = \arcsin(-0.75) + k(2\pi)\) o\(x = (\pi - \arcsin(-0.75)) + k(2\pi)\), donde\(k\) es un número entero.

Ejercicio\(\PageIndex{32}\)

Para cada una de las ecuaciones de las siguientes ecuaciones, utilice una función trigonométrica inversa para escribir los valores exactos de todas las soluciones de la ecuación en el intervalo indicado. Luego use la propiedad periódica de la función trigonométrica para escribir fórmulas que puedan ser utilizadas para generar todas las soluciones de la ecuación dada.

1. \(\sin(x) + 2 = 2.4\)con\(-\pi \leq x \leq \pi\)
2. \(5\cos(x) + 3 = 7\)con\(-\pi \leq x \leq \pi\)
3. \(2\tan(x) + 4 = 10\)con\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\)
4. \(-3.8\sin(x) + 7 = 10\)con\(-\pi \leq x \leq \pi\)
5. \(8\cos(x) + 7 = 2\)con\(-\pi \leq x \leq \pi\)

Responder

(a)\(x = \sin^{-1}(0.4) + k(2\pi)\) o\(x = (\pi - \sin^{-1}(0.4)) + k(2\pi)\), donde\(k\) es un entero.

b)\(x = \cos^{-1}(\dfrac{4}{5}) + k(2\pi)\) o\(x = -\cos^{-1}(\dfrac{4}{5}) + k(2\pi)\), donde\(k\) es un número entero.

Ejercicio\(\PageIndex{33}\)

Determinar los valores exactos de las soluciones de la ecuación dada en un periodo completo de la función trigonométrica que se utiliza en la ecuación. Luego use la propiedad periódica de la función trigonométrica para escribir fórmulas que puedan ser utilizadas para todas las soluciones de la ecuación dada.

1. \(4\sin(2x) = 3\)
2. \(4\cos(2x) = 3\)
3. \(\cos(\pi x) = 0.6\)
4. \(\sin(\pi x - \dfrac{\pi}{4}) = 0.2\)
5. \(\cos(\pi x - \dfrac{\pi}{4}) = 0.2\)

Responder

(a) El periodo para la función trigonométrica es\(\pi\). Primero resolvemos la ecuación\(4\sin(t) = 3\) con\(-\pi \leq t \leq \pi\) y obtenemos\(t = \sin^{-1}(0.75) + k(2\pi)\) o\(t = (\pi - \sin^{-1}(0.75)) + k(2\pi)\). Luego usamos la sustitución\(t = 2x\) para obtener\(x = \dfrac{1}{2}\sin^{-1}(0.75) + k\pi\) o\(x = \dfrac{1}{2}(\pi - \sin^{-1}(0.75)) + k\pi\), donde\(k\) es un número entero.

d) El periodo para la función trigonométrica es\(2\). Primero resolvemos la ecuación\(\sin(t) = 0.2\) con\(-\pi \leq t \leq \pi\) y obtenemos\(t = \sin^{-1}(0.2) + k(2\pi)\) o\(t = (\pi - \sin^{-1}(0.2)) + k(2\pi)\). Ahora usamos la sustitución\(t = \pi x - \dfrac{\pi}{4}\) para obtener\(x = \dfrac{1}{\pi}\sin^{-1}(0.2) + \dfrac{1}{4}\) o\(x = -\dfrac{1}{\pi} + \dfrac{5}{4}) + 2k\), donde\(k\) es un entero.

Ejercicio\(\PageIndex{34}\)

En el Ejemplo 2.17 de la página 2.17, utilizamos métodos gráficos para encontrar dos soluciones de la ecuación\[35\cos(\dfrac{5\pi}{3}t) + 105 = 100\]

Encontramos que dos soluciones fueron\(t \approx 0.3274\) y\(t \approx 0.8726\). Reescribe esta ecuación y luego usa la función coseno inverso para determinar los valores exactos de estas dos soluciones. Luego usa el periodo de la función\(35\cos(\dfrac{5\pi}{3}t) + 105\) para escribir fórmulas que puedan ser utilizadas para generar todas las soluciones de la ecuación dada.