3.3: Triángulos que no son triángulos rectos

Última actualización
Guardar como PDF

Page ID: 113330

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

¿Qué es la Ley de los Senos?
¿Qué información necesitamos de un triángulo para aplicar la Ley de Sines?
¿Qué entendemos por el caso ambiguo para la Ley de los Sines? ¿Por qué es ambiguo?
¿Qué es la Ley de los Cosinos?
¿Qué información necesitamos de un triángulo para aplicar la Ley de Cosinos?

En la Sección 3.2 aprendimos a usar las funciones trigonométricas y se dio información sobre un triángulo rectángulo para determinar otras partes de ese triángulo rectángulo. Por supuesto, hay muchos triángulos sin ángulos rectos (estos triángulos se llaman triángulos oblicuos). Nuestra siguiente tarea es desarrollar métodos para relacionar lados y ángulos de triángulos oblicuos. En esta sección, desarrollaremos dos de tales métodos, la Ley de los Sinos y la Ley de los Cosinos. En la siguiente sección, aprenderemos a usar estos métodos en aplicaciones.

Al igual que con los triángulos rectos, vamos a querer alguna notación estándar cuando se trabaja con triángulos generales. Nuestra notación será similar a la que usamos para los triángulos rectos. En particular, a menudo dejaremos que las longitudes de los tres lados de un triángulo sean$a$,$b$, y$c$. Los ángulos opuestos a los lados de longitud$a$$b$,, y$c$ serán etiquetados$\alpha$,$\beta$, y$\gamma$ respectivamente (Figura$\PageIndex{1}$).

A veces etiquetaremos los vértices del triángulo como A, B y C como se muestra en la Figura$\PageIndex{1}$.

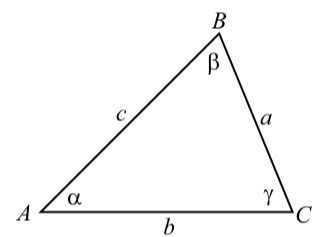
$3.12.png$

Figura$\PageIndex{1}$: Etiquetado estándar para un triángulo

Actividad inicial

Antes de exponer la Ley de Sinos y la Ley de Cosinos, vamos a utilizar dos aplicaciones de Geogebra para explorar las relaciones sobre las partes de un triángulo. En cada una de estas aplicaciones, se dibuja un triángulo. Se muestran las longitudes de los lados del triángulo y la medida para cada uno de los ángulos. El tamaño y la forma del triángulo se pueden cambiar arrastrando uno (o todos) de los puntos que forman los vértices del triángulo.

1. Abre la app Geogebra llamada La Ley de Sines en http://gvsu.edu/s/01B

Experimenta moviendo los vértices del triángulo y observando lo que sucede con las longitudes y los ángulos y los cálculos mostrados en la parte inferior izquierda de la pantalla.
Usa un triángulo en particular y verifica los cálculos mostrados en la parte inferior izquierda de la pantalla. Redondee sus resultados a la milésima más cercana como se hace en la aplicación.
Escribe una ecuación (o ecuaciones) que esta app esté ilustrando. Esto será parte de la Ley de los Sines.

2. Abre la app Geogebra llamada La ley de los cosenos en http://gvsu.edu/s/01C

Experimenta moviendo los vértices del triángulo y observando lo que sucede con las longitudes y los ángulos y los cálculos mostrados en la parte inferior izquierda de la pantalla.
Usa un triángulo en particular y verifica los cálculos mostrados en la parte inferior izquierda de la pantalla. Redondee sus resultados a la milésima más cercana como se hace en la aplicación.
Escribe una ecuación que esta app esté ilustrando. Esto será parte de la Ley de Cosinos.

La ley de los senos

La primera parte de la actividad inicial tenía por objeto ilustrar la Ley de los Sines. A continuación se presenta una declaración formal de la Ley de Sines.

Ley de Sines

En un triángulo, si$a$,$b$, y$c$ son las longitudes de los lados opuestos ángulos$\alpha$,$\beta$, y$\gamma$, respectivamente, entonces

\[\dfrac{\sin(\alpha)}{a} = \dfrac{\sin(\beta)}{b} = \dfrac{\sin(\gamma)}{c}\]

Esto es equivalente a

\[\dfrac{a}{\sin(\alpha)} = \dfrac{b}{\sin(\beta)} = \dfrac{c}{\sin(\gamma)}\]

Tenga en cuenta que la Ley de Sines en realidad tiene tres ecuaciones condensadas en una sola línea. Las tres ecuaciones son:

\[\dfrac{\sin(\alpha)}{a} = \dfrac{\sin(\beta)}{b}\]\[\dfrac{\sin(\alpha)}{a} = \dfrac{\sin(\gamma)}{c}\]\[\dfrac{\sin(\beta)}{b} = \dfrac{\sin(\gamma)}{c}\]

La clave para usar la Ley de los Sinos es que cada ecuación involucra 4 cantidades, y si conocemos 3 de estas cantidades, podemos usar la Ley de Sines para determinar la cuarta. Estas 4 cantidades son en realidad dos pares diferentes, donde un elemento de un par es un ángulo y el otro elemento de ese par es la longitud del lado opuesto a ese ángulo. En la Figura$\PageIndex{2}$,$\theta$ y$x$ formar uno de esos pares, y$\phi$ y$y$ son otro de esos pares. Podemos escribir la Ley de los Sines de la siguiente manera:

$3.13.png$

Figura$\PageIndex{2}$: Diagrama para la Ley de los Senos

Ley de Sines

En un triángulo, si$x$ es la longitud del lado opuesto al ángulo$\theta$ y$y$ es la longitud del lado opuesto al ángulo$\phi$, entonces

\[\dfrac{x}{\sin(\theta)} = \dfrac{y}{\sin(\phi)}\]o\[\dfrac{\sin(\theta)}{x} = \dfrac{\sin(\phi)}{y}. \label{lawofsines}\]

Ejemplo$\PageIndex{1}$: Using the Law of Sines

Supongamos que las medidas de dos ángulos de un triángulo son$25^\circ$ y$51.3^\circ$ y que el lado opuesto al$25^\circ$ ángulo es de 12 pies de largo. Utilizaremos la Ley de los Sinos para determinar las otras tres partes del triángulo. (Recuerda que a menudo decimos que estamos “resolviendo el triángulo”). El primer paso es dibujar un diagrama razonable y preciso del triángulo y etiquetar las partes. Esto se muestra en el siguiente diagrama.

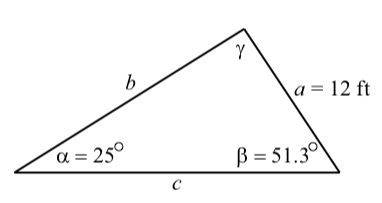
$Ejemplo 3.13.png$

Notamos que conocemos los valores de la longitud de un lado y sus ángulos opuestos ($a$y$\alpha$). Ya que también conocemos el valor de$\beta$, podemos utilizar la Ley de los Sinos para determinar$b$. Esto se hace de la siguiente manera:

\[\dfrac{a}{\sin(\alpha)} = \dfrac{b}{\sin(\beta)}\]\[b = \dfrac{a\sin(\beta)}{\sin(\alpha)}\]\[b = \dfrac{12\sin(51.3^\circ)}{\sin(25^\circ)}\]\[b \approx 22.160\]

Entonces vemos que el lado opuesto al$51.3^\circ$ ángulo es de unos 22.160 pies de largo. Todavía tenemos que determinar$\gamma$ y$c$. Usaremos el hecho de que la suma de los ángulos de un triángulo es igual$180^\circ$ a para determinar$\gamma$.
Ahora que sabemos$\gamma$, podemos utilizar de nuevo la Ley de los Sinos para determinar$c$. Para ello, resolvemos la siguiente ecuación para$c$.

\[\dfrac{a}{\sin(\alpha)} = \dfrac{c}{\sin(\gamma)}\]

Debemos verificar que el resultado es$c \approx 27.587$ pies. Para verificar nuestros resultados, debemos verificar que para este triángulo,\[\dfrac{\sin(\alpha)}{a} = \dfrac{\sin(\beta)}{b} = \dfrac{\sin(\gamma)}{c} \approx 0.035.\]

Ejercicio$\PageIndex{1}$

Supongamos que las medidas de dos ángulos de un triángulo son$15^\circ$$135^\circ$ y y que el lado que es común a estos dos ángulos es$71$ pulgadas de largo. A continuación se presenta un diagrama razonablemente preciso para este triángulo.

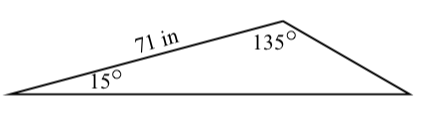
$pc 3.14.png$

Determinar las longitudes de los otros dos lados del triángulo y la medida del tercer ángulo. Pista: Primero introduce alguna notación apropiada, determina la medida del tercer ángulo y luego usa la Ley de los Sines.

Contestar

Primero notamos que el tercer ángulo en el triángulo es$30^\circ$ ya que la suma de los dos ángulos dados es$150^\circ$. Dejamos x ser la longitud del lado opuesto al$15^\circ$ ángulo y dejamos$y$ ser la longitud del lado opuesto al$135^\circ$ ángulo. Entonces vemos que

\[\dfrac{x}{\sin(15^\circ)} = \dfrac{71}{\sin(30^\circ)}\]
\[x = \dfrac{71\sin(15^\circ)}{\sin(30^\circ)}\]
\[x \approx 36.752\]

\[\dfrac{y}{\sin(135^\circ)} = \dfrac{71}{\sin(30^\circ)}\]
\[y = \dfrac{71\sin(135^\circ)}{\sin(30^\circ)}\]
\[y \approx 100.409\]

Entonces la longitud del lado opuesto al$15^\circ$ ángulo es de aproximadamente$36.75$ pulgadas, y la longitud del lado opuesto al$135^\circ$ ángulo es de aproximadamente$100.41$ pulgadas.

Uso de la Ley de los Senos para Determinar un Ángulo

Como hemos dicho, una ecuación para la Ley de los Sinos involucra cuatro cantidades, dos ángulos y las longitudes de los dos lados opuestos a estos ángulos. En los ejemplos que hemos mirado, se han dado dos ángulos y un lado. Luego se utilizó la Ley de los Sines para determinar la longitud del otro lado.

Podemos encontrarnos con una ligera complicación cuando queremos determinar un ángulo usando la Ley de los Sines. Esto puede ocurrir cuando se nos dan las longitudes de dos lados y la medida de un ángulo opuesto a uno de estos lados. El problema es que hay dos ángulos diferentes entre$0^\circ$ y$180^\circ$ que son soluciones de una ecuación de la forma$\sin(\theta) = $ “un número entre$0$ y$1$”.
Por ejemplo, considere la ecuación$\sin(\theta) = 0.7$. Podemos usar la función sinusoidal inversa para determinar una solución de esta ecuación, que es\[\theta_{1} = \sin^{-1}(0.7) \approx 44.427^\circ.\]

La función sinusoidal inversa nos da la solución que está entre$0^\circ$ y$90^\circ$, es decir, la solución en el primer cuadrante. Hay una segunda solución a esta ecuación en el segundo cuadrante, es decir, entre$90^\circ$ y$180^\circ$. Esta segunda solución es$\theta_{2} = 180^\circ - \theta_{1}$. Entonces en este caso,\[\theta_{2} = 180^\circ - \sin^{-1}(0.7) \approx 135.573^\circ.\]
Las próximas dos comprobaciones de progreso serán actividades guiadas a través de ejemplos donde necesitaremos usar la Ley de Sines para determinar un ángulo.

Ejercicio$\PageIndex{2}$

Supongamos que un triángulo tiene un lado de longitud$2$ pies que es un lado adyacente para un ángulo de$40^\circ$. ¿Es posible que el lado opuesto al$40^\circ$ ángulo tenga una longitud de$1.7$ pies?

Para tratar de responder a esto, primero dibujamos un diagrama razonablemente exacto de la situación como se muestra a continuación.

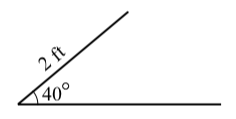
$pc 3.15.png$

La línea horizontal no es un lado del triángulo (todavía). Por ahora, solo lo estamos usando como uno de los lados del$40^\circ$ ángulo. Además, no hemos dibujado el lado opuesto al$40^\circ$ ángulo ya que solo por observación, parece que podría haber dos formas posibles de dibujar un lado de longitud 3 pies. Ahora llegamos a los detalles.

Dejar$\theta$ ser el ángulo opuesto al lado de longitud 2 pies. Utilizar la Ley de los Senos para determinar$\sin(\theta)$.
Utilice la función sinusoidal inversa para determinar una solución (redondeada a la décima de grado más cercana) para$\theta$. Llama a esta solución$\theta_{1}$.
Dejar$\theta_{2} = 180^\circ - \theta_{1}$ Explicar por qué (o verificar que) también$\theta_{2}$ es una solución de la ecuación en la parte (1).

Esto quiere decir que podría haber dos triángulos que satisfagan las condiciones del problema.

Determinar el tercer ángulo y el tercer lado cuando$2$ es el ángulo opuesto al lado de longitud$\theta_{1}$.
Determinar el tercer ángulo y el tercer lado cuando$2$ es el ángulo opuesto al lado de longitud$\theta_{2}$.

Contestar

1. El lado opuesto al ángulo de$40^\circ$ tiene$1.7$ pies de longitud. Así que conseguimos

\[\dfrac{\sin(\theta)}{2} = \dfrac{\sin(40^\circ)}{1.7}\]
\[\sin(\theta) = \dfrac{2\sin(40^\circ)}{1.7} \approx 0.75622\]
2. Vemos que

\[\theta_{1} = \sin^{-1}(\dfrac{2\sin(40^\circ)}{1.7}) \approx 49.132^\circ\]

3. $\theta_{2} = 180^\circ - \theta_{1} \approx 130.868^\circ$. El uso de ángulos de referencia en lugar de arcos de referencia,$\theta_{1}$ es el ángulo de referencia para$\theta_{2}$, que está en el segundo cuadrante. Por lo tanto,$\sin(\theta_{2}) = \sin(\theta_{1})$

4. El tercer ángulo se$\alpha$ puede determinar usando la suma de los ángulos de un triángulo.

\[\alpha + \theta_{1} + 40^\circ = 180^\circ\]

\[\alpha \approx 180^\circ - 40^\circ - 49.132^\circ\]

\[\alpha \approx 90.868^\circ\]

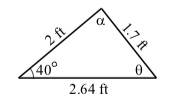
Utilizamos la Ley de los Sinos para determinar la longitud$x$ del lado opuesto$\alpha$. El triángulo resultante se muestra a la derecha.

\[\dfrac{x}{\sin(\alpha)} = \dfrac{1.7}{\sin^(40^\circ)}\]

\[x = \dfrac{1.7\sin(\alpha)}{\sin(40^\circ)}\]

\[x \approx 2.644\space ft\]

$3.15.png$

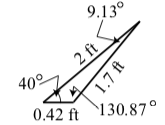
5. Usando el mismo procedimiento que hicimos en la parte (4), obtenemos

\[\theta_{2} \approx 130.868^\circ\]

\[\theta_{2} \approx 9.132^\circ\]

\[x_{2} \approx 0.420\space ft\]

El triángulo se muestra a la derecha.

$3.15 5.png$

Hay momentos en que la Ley de Sines demostrará que no hay triángulos que cumplan ciertas condiciones. A menudo vemos esto cuando una ecuación la Ley de Sines produce una ecuación de la forma\[\sin(\theta) = p\]

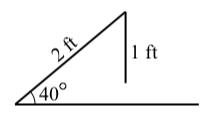
donde$p$ es el número real pero no está entre 0 y 1. Por ejemplo, cambiar las condiciones en la Comprobación de Progreso 3.15 para que queramos un triángulo que tenga un lado de longitud 2 pies que sea un lado adyacente para un ángulo de$40^\circ$ y el lado opuesto al$40^\circ$ ángulo sea tener una longitud de 1 pie. Al igual que en Progreso Comprobación 3.15, dejamos$\theta$ ser el ángulo opuesto al lado de longitud 2 pies y usamos la Ley de Senos para obtener

\[\dfrac{\sin(\theta)}{2} = \dfrac{\sin(40^\circ)}{1}\]

\[\sin(\theta) = \dfrac{2\sin(40^\circ)}{1} \approx 1.2856\]

No existe tal ángulo$\theta$ y esto demuestra que no existe ningún triángulo que cumpla con las condiciones especificadas. El diagrama de la derecha ilustra la situación.

$p197.png$

Ejercicio$\PageIndex{3}$

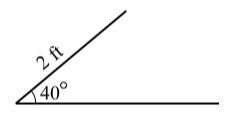
$pc 3.16.png$

Contestar

La única diferencia entre esta y la Comprobación de Progreso 3.15 está en la longitud del lado opuesto al$40^\circ$ ángulo. Podemos usar el mismo diagrama. Por observación, parece que es probable que solo haya manera de dibujar un lado de$3$ pies de longitud. Ahora llegamos a los detalles.

Dejar$\theta$ ser el ángulo opuesto al lado de los$2$ pies de longitud. Utilizar la Ley de los Senos para determinar$\sin(\theta)$. Utilice la función sinusoidal inversa para determinar una solución (redondeada a la décima de grado más cercana) para$\theta$. Llama a esta solución$\theta_{1}$.

Esto quiere decir que podría haber dos triángulos que satisfagan las condiciones del problema.

Determinar el tercer ángulo y el tercer lado cuando el ángulo opuesto al lado de longitud 2 es$\theta_{1}$. Determinar el tercer ángulo y el tercer lado cuando$2$ es el ángulo opuesto al lado de longitud$\theta_{2}$. Ahora determina la suma$40^\circ + \theta_{2}$ y explica por qué esto no es posible en un triángulo.

Let$\theta_{2} = 180^\circ - \theta_{1}$
Explicar por qué (o verificar que) también$\theta_{2}$ es una solución de la ecuación en la parte (1).

Ley de Cosinos

Hemos visto cómo se puede utilizar la Ley de Sines para determinar información sobre lados y ángulos en triángulos oblicuos. Sin embargo, para usar la Ley de Desde (Ecuación\ ref {lawofsines}) necesitamos conocer tres piezas de información. Necesitamos conocer un ángulo y la longitud de su lado opuesto, y además, necesitamos conocer otro ángulo o la longitud de otro lado. Si tenemos tres piezas diferentes de información como las longitudes de dos lados y el ángulo incluido entre ellos o las longitudes de los tres lados, entonces necesitamos un método diferente para determinar las otras piezas de información sobre el triángulo. Aquí es donde es útil la Ley de Cosinos.

Primero exploramos la Ley de Cosinos en la actividad inicial para esta sección. A continuación se presenta la declaración formal habitual de la Ley de Cosinos. Al término de este apartado se incluye el comprobante de la Ley de Cosinos.

Ley de Cosinos

En un triángulo, si$a$,$b$, y$c$ son las longitudes de los lados opuestos ángulos$\alpha$,$\beta$, y$\gamma$, respectivamente, entonces

\[c^{2} = a^{2} + b^{2} - 2ab\cos(\gamma)\]

\[b^{2} = a^{2} + c^{2} - 2ac\cos(\beta)\]

\[a^{2} = b^{2} + c^{2} - 2bc\cos(\alpha)\]

Al igual que con la Ley de los Sinos, hay tres ecuaciones en la Ley de los Sinos. No obstante, podemos recordar esto con una sola ecuación ya que la clave para utilizar la Ley de Cosinos es que esta ley involucra 4 cantidades. Estas 4 cantidades son las longitudes de los tres lados y la medida de uno de los ángulos del triángulo como se muestra en la Figura 3.14.

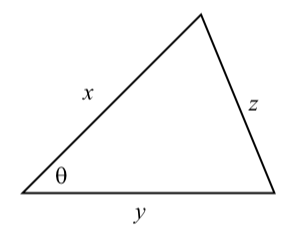
$3.14.png$

Figura$\PageIndex{3}$: Diagrama para la Ley de Cosinos

En este diagrama, se encuentran las longitudes de los tres lados y$\theta$ es el ángulo entre los lados$x$ y$y$. Theta también se puede considerar como el ángulo de lados opuestos. Así podemos escribir la Ley de Cosinos de la siguiente manera:

Ley de Cosinos

En un triángulo, si$x$,$y$, y$z$ son las longitudes de los lados de un triángulo y$\theta$ es el ángulo entre los lados$x$ y$y$ como en la Figura$\PageIndex{3}$, entonces

\[z^{2} = x^{2} + y^{2} - 2xy\cos(\theta).\]

La idea es que si conoces 3 de estas 4 cantidades, puedes usar la Ley de Cosinos para determinar la cuarta cantidad. La Ley de Cosinos involucra las longitudes de los tres lados de un triángulo y un ángulo. Afirma que:

El cuadrado del lado opuesto a un ángulo es la suma de los cuadrados de los dos lados del ángulo menos dos veces el producto de los dos lados del ángulo y el coseno del ángulo.

Exploraremos el uso de la Ley de Cosinos en la próxima comprobación de progreso.

Ejercicio$\PageIndex{4}$

Dos lados de un triángulo tienen$2.5$ metros de longitud y$3.5$ metros, y el ángulo formado por estos dos lados tiene una medida de$60^\circ$. Determinar las otras partes del triángulo.

El primer paso es dibujar un diagrama razonablemente preciso del triángulo y etiquetar las partes. Esto se muestra en el diagrama a continuación.

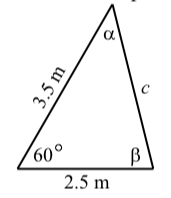
$pc 3.17.png$

Usa la Ley de Cosinos para determinar la longitud del lado opuesto al$60^\circ$ ángulo. ($c$). Ahora conocemos un ángulo ($60^\circ$) y la longitud de su lado opuesto. Podemos usar la Ley de los Sinos para determinar los otros dos ángulos. No obstante, recuerde que debemos tener cuidado al usar la Ley de los Senos para determinar un ángulo ya que la ecuación puede producir dos ángulos.
Usa la Ley de Sines para$\sin(\alpha)$ determinar .Determinar los dos valores posibles para$\alpha$ y explicar por qué uno de ellos no es posible.
Usa el hecho de que la suma de los ángulos de un triángulo es$180^\circ$ para determinar el ángulo$\beta$.
Usa la Ley de Sines para verificar los resultados.

Contestar

1. Utilizando la Ley de Cosinos, obtenemos

\[c^{2} = 3.5^{2} + 2.5^{2} - 2(3.5)(2.5)\cos(60^\circ) = 9.75\]

Entonces$c = \sqrt{9.75} \approx 3.12250\space ft$
2. Usando la Ley de Sines, obtenemos

\[\dfrac{\sin(\alpha)}{2.5} = \dfrac{\sin(60^\circ)}{c}\]

\[\sin(\alpha) = \dfrac{2.5\sin(60^\circ)}{c} \approx 0.69338\] $página385imagen770554416$

A partir de esto, obtenemos$\alpha \approx 43.898^\circ$ o$\alpha \approx 136.102^\circ$. Sin embargo, dado que el ángulo dado en$60^\circ$, el segundo valor no es posible desde entonces$136.102^\circ + 60^\circ < 180^\circ$. Entonces$\alpha \approx 43.898^\circ$.

Como la suma de los ángulos de un triángulo debe ser$180^\circ$, tenemos\[60^\circ + 43.898^\circ + \beta = 180^\circ\]\[\beta \approx 76.102^\circ\]

Con los valores que hemos determinado, podemos verificar nuestro trabajo demostrando que\[\dfrac{\sin(60^\circ)}{c} = \dfrac{\sin(\alpha)}{2.5} = \dfrac{\beta}{3.5} \approx 0.27735.\]

Se utilizó la Ley de Sines para determinar dos ángulos en Progreso Comprobación 3.17 y vimos que había que tener cuidado ya que la ecuación para la Ley de Sines a menudo produce dos ángulos posibles. Podemos evitar esta situación utilizando la Ley de Cosinos para determinar los ángulos en su lugar. Esto se debe a que una ecuación de la forma$\cos(\theta) = p$, donde p es un número real entre$0$ y$1$ tiene solo una solución para$\theta$ entre$0^\circ$ y$180^\circ$. La idea es resolver una ecuación a partir de la Ley de Cosinos para el coseno del ángulo. En Ejercicio$\PageIndex{4}$, primero determinamos$\theta^{2} = 3.12250$. Entonces podríamos haber procedido de la siguiente manera:

\[2.5^{2} = 3.5^{2} + 3.12250^{2} - 2(3.5)(3.12250)\cos(\alpha)\]
\[2(3.5)(3.12250)\cos(\alpha) = 3.5^{2} + 3.12250^{2} - 2.5^{2}\]
\[\cos(\alpha) = \dfrac{15.75}{21.8575} \approx 0.720577\]

Entonces podemos usar la función coseno inversa y obtener$\alpha \approx 43.898^\circ$, que es lo que obtuvimos en Ejercicio$\PageIndex{4}$.

Ahora podemos usar el hecho de que la suma de los ángulos en un triángulo es$180^\circ$ para determinar$\beta$ pero para completar, también podríamos usar la Ley de Cosinos para determinar$\beta$ y luego usar la suma de ángulos para el triángulo como un cheque de nuestro trabajo.

Ejercicio$\PageIndex{5}$

Los tres lados de un triángulo tienen longitudes de$3$ pies,$5$ pies y$6$ pies. Utilizar la Ley de Cosinos para determinar cada uno de los tres ángulos.

Contestar

El primer paso es dibujar un diagrama razonablemente preciso y etiquetar los ángulos. Usaremos el diagrama de la derecha.

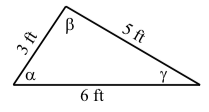
$3.18.png$

Ley de Cosinos, obtenemos

\[5^{2} = 3^{2} + 6^{2} - 2(3)(6)\cos(\alpha)\]\[\cos(\alpha) = \dfrac{20}{36}\]\[\alpha \approx 56.251^\circ\]

\[6^{2}\ = 3^{2} + 5^{2} - 2(3)(5)\cos(\beta)\]\[\cos(\beta) = \dfrac{-2}{30}\]\[\beta \approx 98.823^\circ\]

\[3^{2}\ = 5^{2} + 6^{2} - 2(5)(6)\cos(\gamma)\]\[\cos(\gamma) = \dfrac{52}{60}\]\[\gamma \approx 29.926^\circ\]

Comprobamos estos resultados verificándolo$\alpha + \beta + \gamma = 180^\circ$.

Apéndice — Prueba de la Ley de Sines

Usaremos lo que sabemos de los triángulos rectos para probar la Ley de los Sinos. La idea clave es crear triángulos rectos a partir del diagrama para un triángulo general dibujando una altitud de longitud$h$ desde uno de los vértices. Primero notamos que si$\alpha$,$\beta$, y$\gamma$ son los tres ángulos de un triángulo, entonces\[\alpha + \beta + \gamma = 180^\circ\]

Esto significa que como máximo uno de los tres ángulos puede ser un ángulo obtuso (entre$90^\circ$ y$180^\circ$), y por lo tanto, al menos dos de los ángulos deben ser agudos (menores que$90^\circ$) .La figura 3.15 muestra los dos casos posibles para un triángulo general. El triángulo de la izquierda tiene tres ángulos agudos y el triángulo de la derecha tiene dos ángulos agudos ($\alpha$y$\beta$) y y un ángulo obtuso$\gamma$.

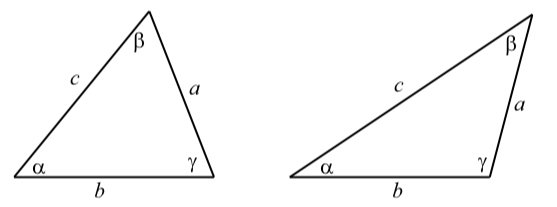
$3.15.png$

Figura$\PageIndex{4}$: Triángulos generales

Ahora probaremos la Ley de Sines para el caso donde los tres ángulos del triángulo son ángulos agudos. La prueba para el caso donde un ángulo del triángulo es obtuso se incluye en los ejercicios. La idea clave es crear triángulos rectos a partir del diagrama para un triángulo general dibujando altitudes en el triángulo como se muestra en la Figura$\PageIndex{5}$ donde$h$ se dibuja una altitud de longitud desde el vértice de ángulo$\beta$ y una altitud de longitud$k$ se dibuja desde el vértice de ángulo $\gamma$

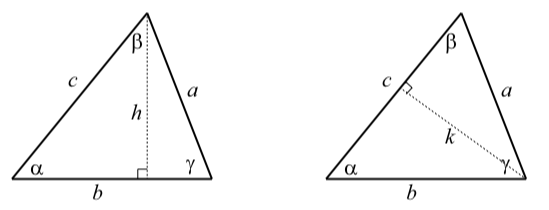
$3.16.png$

Figura$\PageIndex{5}$: Diagrama para la Prueba de la Ley de los Senos

Usando los triángulos derechos en el diagrama de la izquierda, vemos que\[\sin(\alpha) = \dfrac{h}{c}\]\[\sin(\gamma) = \dfrac{h}{a}\]

A partir de esto, podemos concluir que\[h = c\sin(\alpha)\]\[h = a\sin(\gamma)\]

Usando las dos ecuaciones en (1), podemos usar el hecho de que ambos lados derechos son iguales a h para concluir que\[c\sin(\alpha) = a\sin(\gamma)\]
Ahora, dividiendo ambos lados de la última ecuación por$ac$, vemos que

\[\dfrac{\sin(\alpha)}{a} = \dfrac{\sin(\gamma)}{c}\]

Ahora usamos un argumento similar usando el triángulo de la derecha en la Figura$\PageIndex{5}$. Vemos que\[\sin(\alpha) = \dfrac{k}{b}\]\[\sin(\beta) = \dfrac{k}{a}\]

A partir de esto, obtenemos\[k = b\sin(\alpha)\]\[k = a\sin(\beta)\] y así\[b\sin(\alpha) = a\sin(\beta)\]\[\dfrac{\sin(\alpha)}{a} = \dfrac{\sin(\beta)}{b}\]

Ahora podemos usar las ecuaciones (2) y (3) para completar la prueba de la Ley de los Sines,

que es\[\dfrac{\sin(\alpha)}{a} = = \dfrac{\sin(\beta)}{b} = \dfrac{\sin(\gamma)}{c}.\]

Apéndice — Prueba de la Ley de Cosinos

Al igual que con la Ley de Sines, utilizaremos resultados sobre triángulos rectos para probar la Ley de los Cosinos. También usaremos la fórmula de distancia. Comenzaremos con un triángulo general con$a$,$b$, y$c$ representando las longitudes de los lados opuestos a los ángulos$\alpha$,$\beta$, y$\gamma$, respectivamente. Colocaremos el ángulo$\gamma$ en posición estándar en el sistema de coordenadas como se muestra en la Figura$\PageIndex{6}$.

En este diagrama, el ángulo$\gamma$ se muestra como un ángulo obtuso pero la prueba sería la misma si$\gamma$ fuera un ángulo agudo. Hemos etiquetado el vértice de ángulo$\alpha$ como$A$ con coordenadas$(x, y)$ y hemos dibujado una línea desde$A$ perpendicular al$x$ eje -eje. Entonces, a partir de las definiciones de las funciones trigonométricas en la Sección 3.1, vemos que

\[\cos(\gamma) = \dfrac{x}{b}\]\[x = b\cos(\gamma)\]

\[\sin(\gamma) = \dfrac{y}{b}\]\[y = b\sin(\gamma)\]

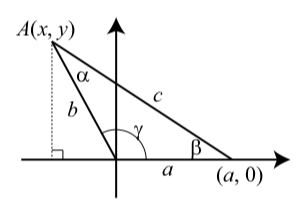
$3.17.png$
Figura$\PageIndex{6}$: Diagrama para la Ley de Cosinos

Ahora usamos la fórmula de distancia con los puntos$A$ y el vértice de ángulo$\beta$, que tiene coordenadas$(a, 0)$. Esto da

\[c = \sqrt{(x - a)^{2} + (y - 0)^{2}}\]
\[c^{2} = (x - a)^{2} + y^{2}\]
\[c^{2} = x^{2} - 2ax + a^{2}+ y^{2}\]

Ahora sustituimos los valores para$x$ y$y$ en la ecuación (4) y obtenemos

\[c^{2} = b^{2}\cos^{2}(\gamma) - 2ab\cos(\gamma) + a^{2} + b^{2}sin^{2}(\gamma)\]
\[c^{2} = a^{2} + b^{2}\cos^{2}(\gamma) + b^{2}sin^{2}(\gamma) - 2ab\cos(\gamma)\]
\[c^{2} = a^{2} + b^{2}(\cos^{2}(\gamma) + sin^{2}(\gamma)) - 2ab\cos(\gamma)\]

Ahora podemos usar la última ecuación y el hecho de que$cos^{2}(\gamma) + \sin^{2}(\gamma) = 1$ para concluir que

\[c^{2} = a^{2} + b^{2} -2ab\cos(\gamma)\]

Esto prueba una de las ecuaciones en la Ley de Cosinos. Las otras dos ecuaciones se pueden probar de la misma manera colocando cada uno de los otros dos ángulos en posición estándar.

Resumen

En esta sección, estudiamos los siguientes conceptos e ideas importantes:

La Ley de los Sinos y la Ley de los Cosinos pueden utilizarse para determinar las longitudes de los lados de un triángulo y la medida de los ángulos de un triángulo.

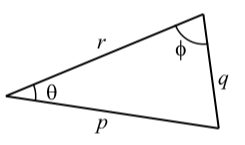
$summary.png$

La Ley de Sines establece que si q es la longitud del lado opuesto al ángulo$\theta$ y$p$ es la longitud del lado opuesto al ángulo$\theta$, entonces\[\dfrac{\sin(\theta)}{q} = \dfrac{\sin(\phi)}{p}\]

La Ley de Cosinos establece que si$p$,$q$, y$r$ son las longitudes de los lados de un triángulo y$\theta$ son los ángulos opuestos al lado$q$, entonces

\[q^{2} = p^{2} + r^{2} - 2pr\cos(\theta).\]

Cada una de las ecuaciones en la Ley de los Sinos y la Ley de los Cosinos involucra cuatro variables. Entonces, si conocemos los valores de tres de las variables, entonces podemos usar la ecuación apropiada para resolver para la cuarta variable.