3.5: Vectores desde un punto de vista geométrico

Última actualización
Guardar como PDF

Page ID: 113348

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

¿Qué es un vector?
¿Cómo utilizamos la forma geométrica de los vectores para encontrar la suma de dos vectores?
¿Cómo usamos la forma geométrica de los vectores para encontrar un múltiplo escalar de un vector?
¿Cómo utilizamos la forma geométrica de los vectores para encontrar la diferencia de dos vectores?
¿Cuál es el ángulo entre dos vectores?
¿Por qué la fuerza es un vector y cómo usamos vectores y triángulos para determinar las fuerzas que actúan sobre un objeto?

Todos hemos tenido la experiencia de dejar caer algo y verlo caer al suelo. Lo que está sucediendo, por supuesto, es que la fuerza de la gravedad está provocando que el objeto caiga al suelo. De hecho, experimentamos la fuerza de la gravedad todos los días simplemente por estar en la Tierra. El peso de cada persona es una medida de la fuerza de gravedad ya que las libras son una unidad de fuerza. Entonces, cuando una persona pesa 150 libras, significa que la gravedad está ejerciendo una fuerza de 150 libras directamente hacia abajo sobre esa persona. Observe que describimos esto con una cantidad y una dirección (recto hacia abajo). Tal cantidad (con magnitud y dirección) se llama vector.

Ahora supongamos que esa persona que pesa 150 libras está de pie en una colina. En matemáticas, simplificamos la situación y decimos que la persona está de pie sobre un plano inclinado como se muestra en la Figura 3.20. (Al hacer del cerro una línea recta, simplificamos las matemáticas involucradas.) El diagrama de la Figura$\PageIndex{1}$, un objeto se encuentra en el plano inclinado en el punto$P$. El plano inclinado hace un ángulo de$\theta$ con la horizontal. El vector$\textbf{w}$ muestra el peso del objeto (fuerza de gravedad, recto hacia abajo). El diagrama también muestra otros dos vectores. El vector$\textbf{b}$ es perpendicular

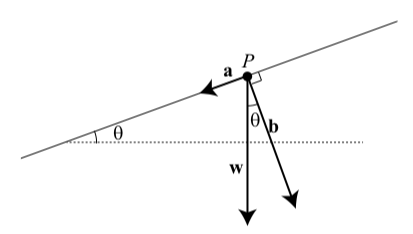
$3.20.png$

Figura$\PageIndex{1}$: Plano Inclinado

al plano representa la fuerza que el objeto ejerce sobre el plano. El vector$\textbf{a}$ es perpendicular$\textbf{b}$ y paralelo al plano inclinado. Este vector representa la fuerza de gravedad a lo largo del plano. En esta y en la siguiente sección, aprenderemos más sobre estos vectores y cómo determinar las magnitudes de estos vectores. También veremos eso con nuestra definición de la adición de dos vectores que$\textbf{w} = \textbf{a} + \textbf{b}$.

Definiciones

Hay algunas cantidades que requieren sólo un número para describirlas. Llamamos a este número la magnitud de la cantidad. Un ejemplo de ello es la temperatura ya que describimos esto con sólo un número como 68 grados Fahrenheit. Otras cantidades son longitud, área y masa. A estos tipos de cantidades se les suele llamar cantidades escalares. Sin embargo, hay otras cantidades que requieren tanto una magnitud como una dirección. Un ejemplo de ello es la fuerza, y otro es la velocidad. Describiríamos una velocidad con algo así como 45 millas por hora al noroeste. La velocidad y la fuerza son ejemplos de una cantidad vectorial. Otros ejemplos de vectores son la aceleración y el desplazamiento.

Algunos vectores están estrechamente asociados con los escalares. En matemáticas y ciencias, hacemos una distinción entre velocidad y velocidad. La velocidad es un escalar y diríamos algo así como que nuestra velocidad es de 65 millas por hora. No obstante, si usáramos una velocidad, diríamos algo así como 65 millas por hora al este. Esto es diferente a una velocidad de$65$ millas por hora al norte aunque en ambos casos, la velocidad es de 65 millas por hora.

Definiciones: Vectores y Escalares

Un vector es una cantidad que tiene tanto magnitud como dirección.
Un escalar es una cantidad que solo tiene magnitud.

Representación Geométrica de Vectores

Los vectores se pueden representar geométricamente mediante flechas (segmentos de línea dirigida). La punta de flecha indica la dirección del vector, y la longitud de la flecha describe la magnitud del vector.

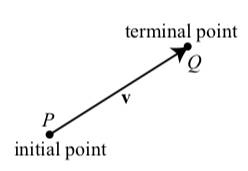
$GRV.png$

Un vector con punto inicial$P$ (la cola de la flecha) y punto terminal$Q$ (la punta de la punta de flecha) puede ser representado por

\[\overrightarrow{PQ}, \textbf{v}, or \overrightarrow{v}.\]

A menudo escribimos$v = \overrightarrow{PQ}$. En este texto, utilizaremos la fuente negrita para designar un vector. Al escribir con lápiz y papel, siempre usamos una flecha sobre la letra (como$\overrightarrow{v}$) para designar un vector. La magnitud (o norma o longitud) del vector$\textbf{v}$ es designada por$\textbf{|v|}$. Es importante recordar que$|\textbf{v}|$ es un número que representa la magnitud o longitud del vector$\textbf{v}$.

Según nuestra definición, un vector posee los atributos de longitud (magnitud) y dirección, pero no se menciona la posición. Entonces consideraremos que dos vectores son iguales si tienen la misma magnitud y dirección. Por ejemplo, si dos autos diferentes viajan a$45$ millas por hora al noroeste (pero en diferentes ubicaciones), tienen vectores de velocidad iguales. Hacemos una definición más formal.

Definición: Vectores iguales

Dos vectores son iguales si y sólo si tienen la misma magnitud y la misma dirección. Cuando los vectores$\textbf{v}$ y$\textbf{w}$ son iguales, escribimos$\textbf{v} = \textbf{v}$.

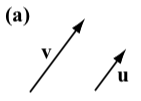
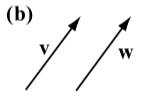
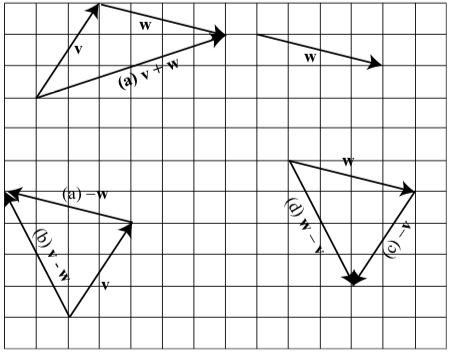
Ejercicio$\PageIndex{1}$

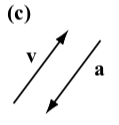
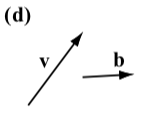
Los siguientes diagramas muestran el vector$\textbf{v}$ junto a otros cuatro vectores. ¿Cuáles (si los hay) de estos cuatro vectores son iguales al vector$\textbf{v}$?

$pc3.24 a.png$ $pc3.24 b.png$ $pc3.24 c.png$ $pc3.24 d.png$

Contestar: El vector$\textbf{w}$ es el único vector que es igual al vector$\textbf{v}$. Vector$\textbf{u}$ tiene la misma dirección que$\textbf{v}$ pero una magnitud diferente. Vector$\textbf{a}$ tiene la misma magnitud que$\textbf{v}$ pero una dirección diferente (tenga en cuenta que la dirección de a es la dirección opuesta de$\textbf{v}$). Vector$\textbf{b}$ tiene una dirección diferente y una magnitud diferente a la$\textbf{v}$.

Operaciones en vectores

Múltiple escalar de un vector

Duplicar una cantidad escalar es simplemente una cuestión de multiplicar su magnitud por$2$. Por ejemplo, si un recipiente tiene$20$ onzas de agua y la cantidad de agua se duplica, entonces tendrá$40$ onzas de agua. ¿Qué queremos decir con duplicar un vector? La idea básica es mantener la misma dirección y multiplicar la magnitud por$2$. Entonces, si un objeto tiene una velocidad de$5$ pies por segundo al sureste y un segundo objeto tiene una velocidad del doble de esa, el segundo objeto tendrá una velocidad de$10$ pies por segundo en dirección sureste. En este caso, decimos que multiplicamos el vector por el escalar$2$. Ahora hacemos una definición que también toma en cuenta que un escalar puede ser negativo.

Definición

Para cualquier vector$\textbf{v}$ y cualquier escalar$c$, el vector$c\textbf{v}$ (llamado múltiplo escalar del vector$\textbf{v}$ es un vector cuya magnitud es$|c|$ multiplicada por la magnitud del vector$\textbf{v}$.

Si$c > 0$, entonces la dirección de$c\textbf{v}$ es la misma que la dirección de$\textbf{v}$.
Si$c < 0$, entonces la dirección de$c\textbf{v}$ es la opuesta a la dirección de$\textbf{v}$.
Si$c = 0$, entonces$c\textbf{v} = 0 \textbf{v} = 0$.

El vector$\textbf{0}$ se llama vector cero y el vector cero no tiene magnitud ni dirección. A veces escribimos$\overrightarrow{0}$ para el vector cero.

En esta definición,$|c|$ se encuentra el valor absoluto del escalar$c$. Se debe tener cuidado de no confundir esto con la notación$\textbf{|v|}$, que es la magnitud del vector$\textbf{v}$. Esta es una razón por la que es importante tener una notación que indique claramente cuándo estamos trabajando con un vector o un escalar.

Adición de vectores

Ilustramos cómo agregar vectores con dos vectores de desplazamiento. Al igual que con la velocidad y la velocidad, existe una distinción entre desplazamiento y distancia. La distancia es un escalar. Entonces podríamos decir que hemos recorrido 2 millas. El desplazamiento, por otro lado, es un vector que consiste en una distancia y una dirección. Entonces los vectores 2 millas al norte y 2 millas al este son diferentes vectores de desplazamiento.

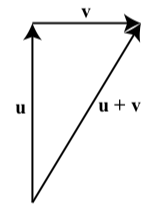
Ahora bien, si viajamos 3 millas al norte y luego viajamos 2 millas al este, terminamos en un punto que define un nuevo vector de desplazamiento. Ver el diagrama a la derecha. En este diagrama,$\textbf{u}$ es “3 millas al norte” y$\textbf{v}$ es “2 millas al este”. La suma vectorial$\textbf{u} + \textbf{v}$ va desde el punto inicial de$\textbf{u}$ hasta el punto terminal de$\textbf{v}$.

$Adición de v.png$

Definición: suma de dos vectores

La suma de dos vectores se define de la siguiente manera: Posicionamos los vectores de manera que el punto inicial de$\textbf{w}$ coincida con el punto terminal de$\textbf{v}$. El vector$\textbf{v} + \textbf{w}$ es el vector cuyo punto inicial coincide con el punto inicial de$\textbf{v}$ y cuyo punto terminal coincide con el punto terminal de$\textbf{w}$.

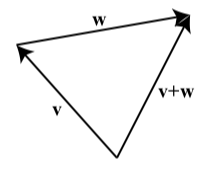
$def.png$

El vector $\ textbf {v} +\ textbf {w}$ se llama la suma o resultante de los vectores$\textbf{v}$ y$\textbf{w}$.

En la definición, observe que los vectores$\textbf{v}$, $\textbf{w}$, y$\textbf{v} + \textbf{w}$ se colocan de manera que el resultado sea un triángulo. Las longitudes de los lados de ese triángulo son las magnitudes de estos lados$|\textbf{v}|$,$|\textbf{w}|$, y$|\textbf{v} + \textbf{w}|$. Si colocamos los dos vectores$\textbf{v}$ y$\textbf{w}$ para que sus puntos iniciales coincidan, podemos usar un paralelogramo para sumar los dos vectores. Esto se muestra en la Figura$\PageIndex{2}$.

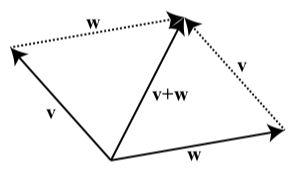
$3.21.png$

Figura$\PageIndex{2}$: Suma de dos vectores usando un paralelogramo

Observe que el vector$\textbf{v}$ forma un par de lados opuestos del paralelogramo al igual que el vector$\textbf{w}$.

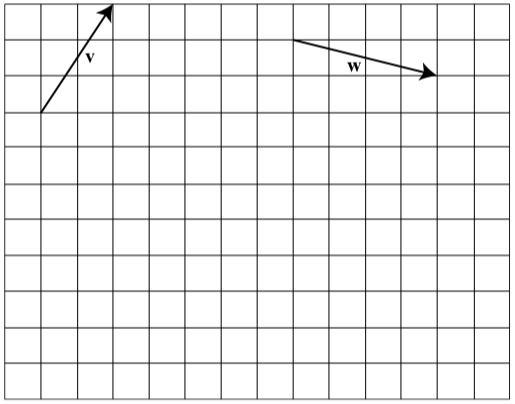
Ejercicio$\PageIndex{2}$

El siguiente diagrama muestra dos vectores,$\textbf{v}$ y$\textbf{w}$. Dibuja los siguientes vectores:

$\textbf{v} + \textbf{w}$
$2\textbf{v}$
$2\textbf{v} + \textbf{w}$
$-2\textbf{w}$
$-2\textbf{w + v}$

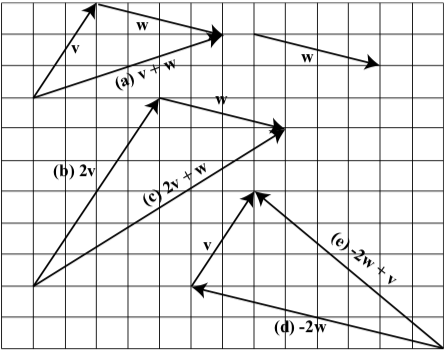
$pc 3.25.png$

Contestar: $3.25.png$

Resta de vectores

Antes de explicar cómo restar vectores, primero explicaremos qué se entiende por el “negativo de un vector”. Esto funciona de manera similar al negativo de un número real. Por ejemplo, sabemos que cuando sumamos$-3$ a$3$, el resultado es$0$. Es decir,$3 + (-3) = 0$

Queremos algo similar para los vectores. Para un vector$\textbf{w}$, la idea es usar el múltiplo escalar$(-1)\textbf{w}$. El vector$(-1)\textbf{w}$ tiene la misma magnitud que$\textbf{w}$ pero tiene la dirección opuesta a$\textbf{w}$. Definimos$-\textbf{w}$ ser$(-1)\textbf{w}$. La figura muestra que cuando sumamos$-\textbf{w}$ a$\textbf{w}$, el punto terminal de la suma es el mismo que el punto inicial de la suma y así el resultado es el vector cero. Es decir,$\textbf{w} + (-\textbf{w}) = \textbf{0}$.

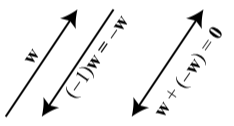
$3.22.png$

Figura$\PageIndex{3}$: La suma de un vector y su negativo

Ahora estamos en condiciones de definir la resta de vectores. La idea es muy similar a la resta de números reales en eso para dos números reales cualesquiera$a$ y$b$,$a - b = a + (-b)$.

Definición: Diferencia entre vectores

Para dos vectores cualesquiera$\textbf{v}$ y$\textbf{w}$, la diferencia entre$\textbf{v}$ y$\textbf{w}$ se denota por$\textbf{v} - \textbf{w}$ y se define de la siguiente manera:

\[\textbf{v} - \textbf{w} = \textbf{v} + (-\textbf{w}).\]

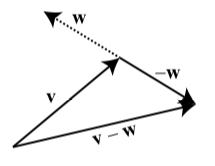
$def2.png$

También decimos que estamos restando el vector$\textbf{w}$ del vector$\textbf{v}$.

Ejercicio$\PageIndex{3}$

El siguiente diagrama muestra dos vectores,$\textbf{v}$ y$\textbf{w}$. Dibuja los siguientes vectores:

$-\textbf{w}$
$\textbf{v - w}$
$-\textbf{v}$
$\textbf{w - v}$

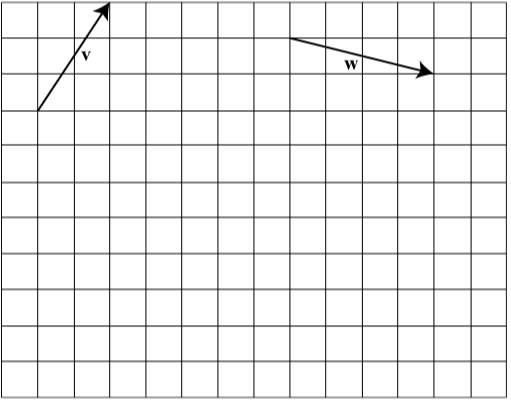
$pc 3.26.png$

Contestar: $3.26.png$

El ángulo entre dos vectores

Hemos visto que podemos usar triángulos para ayudarnos a sumar o restar dos vectores. Las longitudes de los lados del triángulo son las magnitudes de ciertos vectores. Ya que estamos tratando con triángulos, también usaremos ángulos determinados por los vectores.

Definición

El ángulo$\theta$ entre vectores es el ángulo formado por estos dos vectores (con$0^\circ \leq \theta \leq 180^\circ$) cuando tienen el mismo punto inicial.

Entonces en el diagrama de la izquierda en la Figura$\PageIndex{4}$, el ángulo$\theta$ es el ángulo entre los vectores$\textbf{v}$ y$\textbf{w}$. Sin embargo, cuando queremos determinar la suma de dos ángulos, a menudo formamos el paralelogramo determinado por los dos vectores como se muestra en el diagrama de la derecha en la Figura$\PageIndex{3}$. (Consulte la página 422 en el Apéndice C para ver un resumen de las propiedades de un paralelogramo.) Entonces usaremos el ángulo$180^\circ - \theta$ y la Ley de Cosinos ya que nosotros los dos lados del triángulo son las longitudes de$\textbf{v}$ y$\textbf{w}$ y el ángulo incluido es$180^\circ - \theta$. Exploraremos esto en la próxima comprobación de progreso.

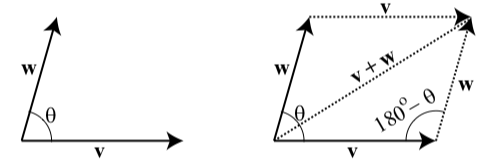
$3.23.png$

Figura$\PageIndex{3}$: Ángulo entre dos vectores

Ejercicio$\PageIndex{4}$

Supongamos que los vectores$\textbf{a}$ y$\textbf{b}$ tienen magnitudes de 80 y 60, respectivamente, y que el ángulo$\theta$ entre los dos vectores es de 53 grados. En la Figura 3.24, hemos dibujado el paralelogramo determinado por estos dos vectores y hemos etiquetado los vértices para referencia.

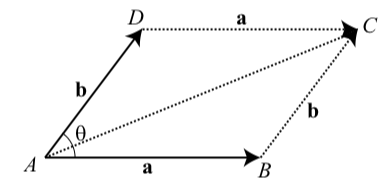
$3.24.png$
Figura 3.24: Diagrama para Comprobación de Progreso 3.27

Recuerde que un vector está determinado por su magnitud y dirección. Determinaremos$|\textbf{a + b}|$ y la medida del ángulo entre$\textbf{a}$ y$\textbf{a + b}$

Determinar la medida de$\angle ABC$.

En$\triangle ABC$, la longitud del lado$AB$ es$|\textbf{a}| = 80$ y la longitud del lado$BC$ es$|\textbf{b}| = 60$. Usa este triángulo y la Ley de Cosinos para determinar la longitud del tercer lado, que es$|\textbf{a + b}|$.

Determinar la medida del ángulo entre$\textbf{a}$ y$\textbf{a + b}$. Esto está$\angle CAB$ en$\triangle ABC$.

Responder

1. $\angle{ABC} = 180^\circ - \theta = 127^\circ$.

2. Usando la Ley de Cosinos, vemos que

\[|\textbf{a} + \textbf{a}|^{2} = |\textbf{a}|^{2} + |\textbf{b}|^{2} - 2|\textbf{a}|\cdot |\textbf{b}|\cos(\angle{ABC}) = 80^{2} + 60^{2} -2\cdot 60 \cdot 80 \cos(127^\circ) = 10000 - 9600\cos(127^\circ) \approx 15777.42422\]así vemos que$|\textbf{a} + \textbf{b} \approx 125.61|.$

3. El ángulo entre los vectores a y a C b es †CAB. En 4ABC, sabemos que †ABC D 127ı, y así †CAB debe ser un ángulo agudo. Utilizaremos la Ley de los Sinos para determinar este ángulo.

\[\dfrac{\sin(\angle{CAB})}{|\textbf{b}|} = \dfrac{\sin(\angle{CAB})}{|\textbf{a} + \textbf{b}|}\]
\[\sin(\angle{CAB} = \dfrac{60\sin(127^\circ)}{|\textbf{a} + \textbf{b}|}\]
\[\sin(\angle{CAB} \approx 0.38148341\]
Entonces el ángulo entre los vectores$\textbf{a}$ y$\textbf{a} + \textbf{b}$ es aproximadamente$22.43^\circ$.

Fuerza

Una cantidad de vector importante es la de la fuerza. En física, una fuerza sobre un objeto se define como cualquier interacción que, cuando se deja sin oposición, cambiará el movimiento del objeto. Entonces una fuerza hará que un objeto cambie su velocidad, es decir, el objeto se acelerará. De manera más informal, una fuerza es un empuje o un tirón sobre un objeto.

Una fuerza que afecta nuestras vidas es la fuerza de la gravedad. La magnitud de la fuerza de gravedad sobre una persona es el peso de esa persona. La dirección de la fuerza de gravedad es recta hacia abajo. Entonces, si una persona que pesa 150 libras se queda quieta en el suelo, entonces el suelo también está ejerciendo una fuerza de 150 libras sobre la persona en dirección ascendente. La fuerza neta sobre la persona estacionaria es cero. Este es un ejemplo de lo que se conoce como equilibrio estático. Cuando un objeto está en equilibrio estático, la suma de las fuerzas que actúan sobre el objeto es igual al vector cero.

Ejemplo$\PageIndex{1}$: Object Suspended from a Ceiling

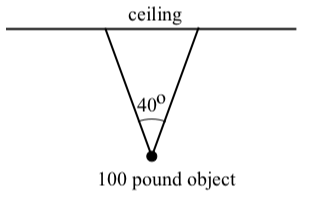
$Ejemplo 3.28.png$

Supongamos que un objeto de 100 libras está suspendido del techo por dos cables que forman un$40^\circ$ ángulo como se muestra en el diagrama a la derecha. Debido a que el objeto es estacionario, los dos cables deben ejercer una fuerza sobre el objeto de manera que la suma de estas dos fuerzas sea igual a 100 libras rectas hacia arriba. (La fuerza de gravedad es de 100 libras hacia abajo.)

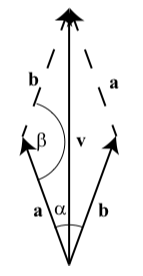
$ejemplo 3.28 2.png$

Supondremos que los dos alambres ejercen unas fuerzas de igual magnitud y que el ángulo entre estas fuerzas y la vertical adentro$20^\circ$. Entonces nuestro primer paso es dibujar una imagen de estas fuerzas, que se muestra a la derecha. El vector$\textbf{v}$ es un vector de magnitud 100 libras. Los vectores$\textbf{a}$ y$\textbf{b}$ son los vectores para las fuerzas ejercidas por los dos hilos. (Tenemos$|\textbf{a}| = |\textbf{b}|$.) También sabemos eso$\alpha = 20^\circ$ y así por las propiedades de los paralelogramos,$\beta = 140^\circ$.

Ejercicio$\PageIndex{5}$

Utilice la trigonometría triangular para determinar la magnitud del vector$\textbf{a}$ en el Ejemplo 3.28. Tenga en cuenta que ya conocemos la dirección de este vector.

Responder

Usando la Ley de los Sines, vemos que

\[\dfrac{|\textbf{a}|}{\sin(20^\circ)} = \dfrac{100}{\sin(140^\circ)}\]
\[|\textbf{a}| = \dfrac{100\sin(20^\circ)}{\sin(140^\circ)}\]
\[|\textbf{a}| \approx 53.21\]
La magnitud del vector a (y del vector b) es aproximadamente$53.21$ libras.

Planos Inclinados

Al inicio de esta sección, discutimos las fuerzas involucradas cuando un objeto se coloca en un plano inclinado. La Figura 3.25 es el diagrama que usamos, pero ahora hemos agregado etiquetas para algunos de los ángulos. Recordemos que el vector$\textbf{w}$ muestra el peso del objeto (fuerza de gravedad, recto hacia abajo), el vector$\textbf{b}$ es perpendicular al plano y representa la fuerza que el objeto ejerce sobre el plano, y el vector$\textbf{a}$ es perpendicular$\textbf{b}$ y paralelo al plano inclinado. Este vector representa la fuerza de gravedad a lo largo del plano. Observe que también hemos agregado una segunda copia del vector a que comienza en la punta del vector$\textbf{b}$.

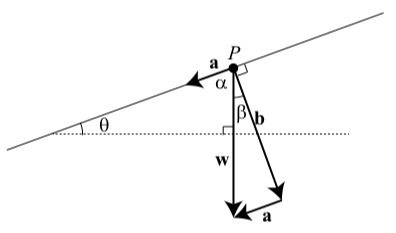
$3.25.png$

Figura 3.25: Plano Inclinado

Usando los ángulos mostrados, vemos que$\alpha + \beta = 90^\circ$ ya que se combinan para formar un ángulo recto, y$\alpha + \theta = 90^\circ$ como son los dos ángulos agudos en un triángulo rectángulo. De esto, concluimos que$\beta = \theta$. Esto nos da la versión final del diagrama de las fuerzas sobre un plano inclinado que se muestra en la Figura 3.26. Observe que los vectores$\textbf{a}$,

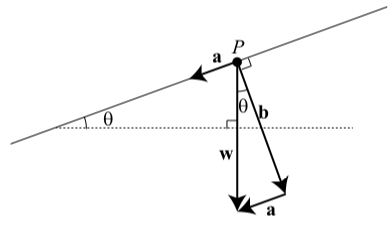
$3.26.png$

Figura 3.26: Plano Inclinado

$\textbf{b}$, y$\textbf{w}$ formar un triángulo rectángulo, y así podemos usar la trigonometría de triángulo rectángulo para problemas de manejo de las fuerzas en un plano inclinado.

Ejercicio$\PageIndex{6}$

Un objeto que pesa$250$ libras se coloca en un plano inclinado que forma un ángulo de$12^\circ$ grados con la horizontal. Usando un diagrama como el de la Figura 3.26, determinar la magnitud de la fuerza contra el plano causada por el objeto y la magnitud de la fuerza hacia abajo del plano sobre el objeto debido a la gravedad.

Nota: La magnitud de la fuerza hacia abajo en el plano será la fuerza en la dirección hacia arriba del plano que se requiere para mantener el objeto estacionario.

Responder

Usando la notación en la Figura 3.26, obtenemos lo siguiente:

\[\dfrac{|\textbf{b}|}{|\textbf{w}|} = \cos(12^\circ)\]
\[\dfrac{|\textbf{a}|}{|\textbf{w}|} = \sin(12^\circ)\]
\[|\textbf{b}| = |\textbf{w}|\cos(12^\circ)\]
\[|\textbf{a}| = |\textbf{w}|\sin(12^\circ)\]
\[|\textbf{b}| \approx 244.54\]
\[|\textbf{a}| \approx 51.98\] $página390imagen792885200$

El objeto ejerce una fuerza de aproximadamente$244.54$ libras perpendiculares al plano y la fuerza de gravedad hacia abajo del plano sobre el objeto es de aproximadamente$51.98$ libras. Entonces, para mantener el objeto estacionario, se debe aplicar al objeto una fuerza de aproximadamente$51.98$ libras por encima del avión.

Resumen

En esta sección, estudiamos los siguientes conceptos e ideas importantes:

Vectores y Escalares
- Un vector es una cantidad que tiene tanto magnitud como dirección.
- Un escalar es una cantidad que solo tiene magnitud.
- Dos vectores son iguales si y sólo si tienen la misma magnitud y la misma dirección.
Múltiple escalar de un vector

Si$c > 0$, entonces la dirección de$c\textbf{v}$ es la misma que la dirección de$\textbf{v}$.
Si$c < 0$, entonces la dirección de$c\textbf{v}$ es la opuesta a la dirección de$\textbf{v}$.
Si$c = 0$, entonces$c\textbf{v} = 0\textbf{v} = 0$.

El vector$\(\textbf{0}$\) se llama vector cero y el vector cero no tiene magnitud ni dirección. A veces escribimos$\overrightarrow{0}$ para el vector cero.

La suma de dos vectores

$def.png$

El vector $\ textbf {v} +\ textbf {w}$ se llama la suma o resultante de los vectores$\textbf{v}$ y$\textbf{w}$.

El ángulo entre dos vectores

El ángulo$\theta$ entre vectores es el ángulo formado por estos dos vectores (con$0^\circ \leq \theta \leq 180^\circ$) cuando tienen el mismo punto inicial.