5.2: La forma trigonométrica de un número complejo

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Cuál es la forma polar (trigonométrica) de un número complejo?
• ¿Cómo multiplicamos dos números complejos en forma polar?
• ¿Cómo dividimos un número complejo en forma polar por un número complejo distinto de cero en forma polar?

Actividad inicial

Si\(z = a + bi\) es un número complejo, entonces podemos trazar\(z\) en el plano como se muestra en la Figura\(\PageIndex{1}\). En esta situación, dejaremos\(r\) ser la magnitud de\(z\) (es decir, la distancia desde\(z\) el origen) y\(\theta\) el ángulo\(z\) hace con el eje real positivo como se muestra en la Figura\(\PageIndex{1}\).

Utilice trigonometría de triángulo rectángulo para escribir\(a\) y\(b\) en términos de\(r\) y\(\theta\).

Explique por qué podemos escribir\(z\) como

\[z = r(\cos(\theta) + i\sin(\theta)). \]

Cuando escribimos\(z\) en la forma dada en Ecuación\(\PageIndex{1}\):, decimos que\(z\) está escrito en forma trigonométrica (o forma polar).

El ángulo\(\theta\) se llama el argumento del argumento del número complejo\(z\) y el número real\(r\) es el módulo o norma de\(z\). Para encontrar la representación polar de un número complejo\(z = a + bi\), primero notamos que

\[r = |z| = \sqrt{a^{2} + b^{2}}\]

\[a = r\cos(\theta)\]

\[b = r\sin(\theta)\]

La multiplicación de números complejos es más complicada que la suma de números complejos. Para comprender mejor el producto de números complejos, primero investigamos la forma trigonométrica (o polar) de un número complejo. Esta forma trigonométrica conecta el álgebra con la trigonometría y será útil para encontrar rápida y fácilmente poderes y raíces de números complejos.

Nota

La palabra polar aquí viene del hecho de que este proceso puede ser visto como ocurriendo con coordenadas polares.

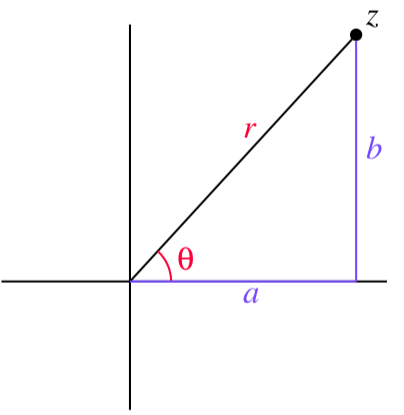
Figura\(\PageIndex{1}\): Forma trigonométrica de un número complejo.

Para encontrar\(\theta\), hay que considerar casos.

• Si\(z = 0 = 0 + 0i\), entonces\(r = 0\) y\(\theta\) puede tener algún valor real.
• Si\(z \neq 0\) y\(a \neq 0\), entonces\(\tan(\theta) = \dfrac{b}{a}\).
• Si\(z \neq 0\) y\(a = 0\) (así\(b \neq 0\)), entonces

\[^* \space \theta = \dfrac{\pi}{2} \space if \space b > 0\]
\[^* \space \theta = -\dfrac{\pi}{2} \space if \space b < 0\]

Ejercicio\(\PageIndex{1}\)

1. Determinar la forma polar de los números complejos\(w = 4 + 4\sqrt{3}i\) y\(z = 1 - i\).
2. Determinar números reales\(a\) y\(b\) para que\(a + bi = 3(\cos(\dfrac{\pi}{6}) + i\sin(\dfrac{\pi}{6}))\)

Contestar

1. Obsérvese eso\(|w| = \sqrt{4^{2} + (4\sqrt{3})^{2}} = 4\sqrt{4} = 8\) y el argumento de\(w\) es\(\arctan(\dfrac{4\sqrt{3}}{4}) = \arctan\sqrt{3} = \dfrac{\pi}{3}\). Entonces

\[w = 8(\cos(\dfrac{\pi}{3}) + \sin(\dfrac{\pi}{3}))\]

También,\(|z| = \sqrt{1^{2} + 1^{2}} = \sqrt{2}\) y el argumento de\(z\) es\(\arctan(\dfrac{-1}{1}) = -\dfrac{\pi}{4}\).

Entonces\[z = \sqrt{2}(\cos(-\dfrac{\pi}{4}) + \sin(-\dfrac{\pi}{4})) = \sqrt{2}(\cos(\dfrac{\pi}{4}) - \sin(\dfrac{\pi}{4})\]

2. Recordemos eso\(\cos(\dfrac{\pi}{6}) = \dfrac{\sqrt{3}}{2}\) y\(\sin(\dfrac{\pi}{6}) = \dfrac{1}{2}\). Entonces\[3(\cos(\dfrac{\pi}{6} + i\sin(\dfrac{\pi}{6})) = 3(\dfrac{\sqrt{3}}{2} + \dfrac{1}{2}i) = \dfrac{3\sqrt{3}}{2} + \dfrac{3}{2}i\]

Entonces\(a = \dfrac{3\sqrt{3}}{2}\) y\(b = \dfrac{3}{2}\).

Hay una representación alternativa que a menudo verás para la forma polar de un número complejo usando un exponencial complejo. No entraremos en los detalles, sino que solo consideraremos esto como notación. Cuando escribimos\(e^{i\theta}\) (donde\(i\) está el número complejo con\(i^{2} = -1\)) nos referimos

\[e^{i\theta} = \cos(\theta) + i\sin(\theta)\]
Entonces la forma polar también se\(r(\cos(\theta) + i\sin(\theta))\) puede escribir como\(re^{i\theta}\):

\[re^{i\theta} = r(\cos(\theta) + i\sin(\theta))\]

Productos de Números Complejos en Forma Polar

Existe una fórmula de producto importante para números complejos que proporciona la forma polar. Ilustramos con un ejemplo.

Ejemplo\(\PageIndex{1}\): Products of Complex Numbers in Polar Form

Dejar\(w = -\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i\) y\(z = \sqrt{3} + i\). Usando nuestra definición del producto de números complejos vemos que

\[wz = (\sqrt{3} + i)(-\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i) = -\sqrt{3} + i.\]
Ahora escribimos\(w\) y\(z\) en forma polar. Obsérvese eso\(|w| = \sqrt{(-\dfrac{1}{2})^{2} + (\dfrac{\sqrt{3}}{2})^{2}} = 1\) y el argumento de\(w\) satisface\(\tan(\theta) = -\sqrt{3}\). Ya que\(w\) está en el segundo cuadrante, vemos eso\(\theta = \dfrac{2\pi}{3}\), por lo que la forma polar de\(w\) es\[w = \cos(\dfrac{2\pi}{3}) + i\sin(\dfrac{2\pi}{3})\]

También,\(|z| = \sqrt{(\sqrt{3})^{2} + 1^{2}} = 2\) y el argumento de\(z\) satisface\(\tan(\theta) = \dfrac{1}{\sqrt{3}}\).

Ya que\(z\) está en el primer cuadrante, lo sabemos\(\theta = \dfrac{\pi}{6}\) y la forma polar de\(z\) es\[z = 2[\cos(\dfrac{\pi}{6}) + i\sin(\dfrac{\pi}{6})]\]

También podemos encontrar la forma polar del producto complejo\(wz\). Aquí tenemos\(|wz| = 2\), y el argumento de\(zw\) satisface\(\tan(\theta) = -\dfrac{1}{\sqrt{3}}\). Ya que\(wz\) está en el cuadrante II, vemos eso\(\theta = \dfrac{5\pi}{6}\) y la forma polar de\(wz\) es\[wz = 2[\cos(\dfrac{5\pi}{6}) + i\sin(\dfrac{5\pi}{6})].\]

Cuando comparamos las formas polares de\(w, z\), y\(wz\) podríamos notar eso\(|wz| = |w||z|\) y que el argumento de\(zw\) es\(\dfrac{2\pi}{3} + \dfrac{\pi}{6}\) o la suma de los argumentos de\(w\) y\(z\). Esto resulta ser cierto en general.

El resultado de Ejemplo no\(\PageIndex{1}\) es coincidencia, como vamos a mostrar. En general, tenemos el siguiente resultado importante sobre el producto de dos números complejos.

Multiplicación de números complejos en forma polar

Dejar\(w = r(\cos(\alpha) + i\sin(\alpha))\) y\(z = s(\cos(\beta) + i\sin(\beta))\) ser números complejos en forma polar. Entonces la forma polar del producto complejo\(wz\) viene dada por

\[wz = rs(\cos(\alpha + \beta) + i\sin(\alpha + \beta))\]

Esto establece que para multiplicar dos números complejos en forma polar, multiplicamos sus normas y sumamos sus argumentos.

Para entender por qué este resultado es cierto en general, dejar\(w = r(\cos(\alpha) + i\sin(\alpha))\) y\(z = s(\cos(\beta) + i\sin(\beta))\) ser números complejos en forma polar. Usaremos coseno y seno de sumas de ángulos identidades para encontrar\(wz\):

\[w = [r(\cos(\alpha) + i\sin(\alpha))][s(\cos(\beta) + i\sin(\beta))] = rs([\cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta)]) + i[\cos(\alpha)\sin(\beta) + \cos(\beta)\sin(\alpha)]\]

Ahora usamos las identidades coseno y suma y vemos que

\(\cos(\alpha + \beta) = \cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta)\)y\(\sin(\alpha + \beta) = \cos(\alpha)\sin(\beta) + \cos(\beta)\sin(\alpha)\).

Usando la ecuación (1) y estas identidades, vemos que

\[w = rs([\cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta)]) + i[\cos(\alpha)\sin(\beta) + \cos(\beta)\sin(\alpha)] = rs(\cos(\alpha + \beta) + i\sin(\alpha + \beta))\]

Una ilustración de esto se da en la Figura\(\PageIndex{2}\). La fórmula para multiplicar números complejos en forma polar nos dice que para multiplicar dos números complejos, sumamos sus argumentos y multiplicamos sus normas.

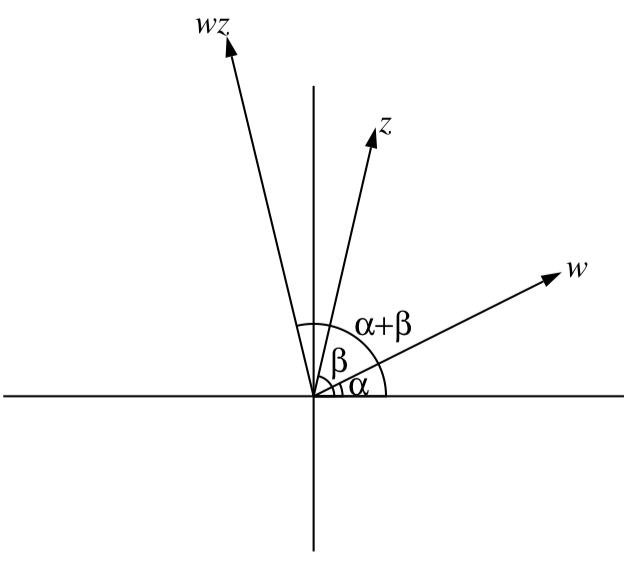
Figura\(\PageIndex{2}\): Una interpretación geométrica de la multiplicación de números complejos.

Ejercicio\(\PageIndex{2}\)

Dejar\(w = 3[\cos(\dfrac{5\pi}{3}) + i\sin(\dfrac{5\pi}{3})]\) y\(z = 2[\cos(-\dfrac{\pi}{4}) + i\sin(-\dfrac{\pi}{4})]\).

1. ¿Qué es\(|wz|\)?
2. ¿Cuál es el argumento de\(wz\)?
3. ¿En qué cuadrante está\(wz\)? Explique.
4. Determinar la forma polar de wz.
5. Dibuja una imagen de\(w\)\(z\),, y\(wz\) que ilustre la acción del producto complejo.

Contestar

1. Desde\(|w| = 3\) y\(|z| = 2\), vemos que

\[|wz| = |w||z| = (3)(2) = 6\]

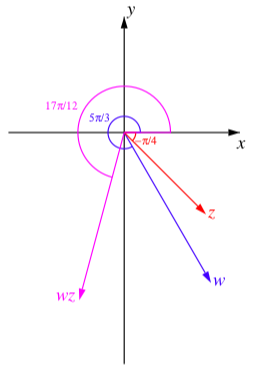
2. El argumento de\(w\) es\(\dfrac{5\pi}{3}\) y el argumento de\(z\) es\(-\dfrac{\pi}{4}\), vemos que el argumento de\(wz\) es\[\dfrac{5\pi}{3} - \dfrac{\pi}{4} = \dfrac{20\pi - 3\pi}{12} = \dfrac{17\pi}{12}\]

3. El lado terminal de un ángulo de\(\dfrac{17\pi}{12} = \pi + \dfrac{5\pi}{12}\) radianes se encuentra en el tercer cuadrante.

4. Conocemos la magnitud y el argumento de\(wz\), por lo que la forma polar de\(wz\) es

\[wz = 6[\cos(\dfrac{17\pi}{12}) + \sin(\dfrac{17\pi}{12})]\]

5. A continuación se presenta una imagen de\(w, z\), y\(wz\) eso ilustra la acción del producto complejo.

Cocientes de números complejos en forma polar

Hemos visto que multiplicamos números complejos en forma polar multiplicando sus normas y sumando sus argumentos. Existe un método similar para dividir un número complejo en forma polar por otro número complejo en forma polar.

División de números complejos en forma polar

Dejar\(w = r(\cos(\alpha) + i\sin(\alpha))\) y\(z = s(\cos(\beta) + i\sin(\beta))\) ser números complejos en forma polar con\(z \neq 0\). Entonces la forma polar del cociente complejo\(\dfrac{w}{z}\) viene dada por\[\dfrac{w}{z} = \dfrac{r}{s}(\cos(\alpha - \beta) + i\sin(\alpha - \beta)).\]

Entonces, para dividir números complejos en forma polar, dividimos la norma del número complejo en el numerador por la norma del número complejo en el denominador y restamos el argumento del número complejo en el denominador del argumento del número complejo en el numerador.

El comprobante de ello es similar a la prueba de multiplicar números complejos y se incluye como complemento a esta sección.

Ejercicio\(\PageIndex{3}\)

Dejar\(w = 3[\cos(\dfrac{5\pi}{3}) + i\sin(\dfrac{5\pi}{3})]\) y\(z = 2[\cos(-\dfrac{\pi}{4}) + i\sin(-\dfrac{\pi}{4})]\).

1. ¿Qué es\(|\dfrac{w}{z}|\)?
2. ¿Cuál es el argumento de\(|\dfrac{w}{z}|\)?
3. ¿En qué cuadrante está\(|\dfrac{w}{z}|\)? Explique.
4. Determinar la forma polar de\(|\dfrac{w}{z}|\).
5. Dibuja una imagen de\(w\)\(z\),, y\(|\dfrac{w}{z}|\) que ilustre la acción del producto complejo.

Contestar

1. Desde\(|w| = 3\) y\(|z| = 2\), vemos que

\[|\dfrac{w}{z}| = \dfrac{|w|}{|z|} = \dfrac{3}{2}\]

2. El argumento de\(w\) es\(\dfrac{5\pi}{3}\) y el argumento de\(z\) es\(-\dfrac{\pi}{4}\), vemos que el argumento de\(\dfrac{w}{z}\) es

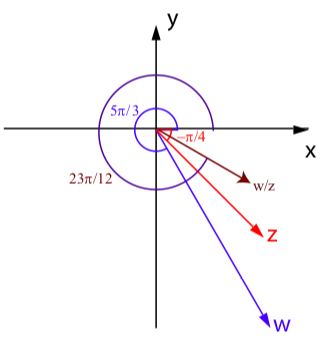
\[\dfrac{5\pi}{3} - (-\dfrac{\pi}{4}) = \dfrac{20\pi + 3\pi}{12} = \dfrac{23\pi}{12}\]

3. El lado terminal de un ángulo de\(\dfrac{23\pi}{12} = 2\pi - \dfrac{\pi}{12}\) radianes se encuentra en el cuarto cuadrante.

4. Conocemos la magnitud y el argumento de\(wz\), por lo que la forma polar de\(wz\) es\[\dfrac{w}{z} = \dfrac{3}{2}[\cos(\dfrac{23\pi}{12}) + \sin(\dfrac{23\pi}{12})]\]

5. A continuación se presenta una imagen de\(w, z\), y\(wz\) eso ilustra la acción del producto complejo.

Prueba de la regla para dividir números complejos en forma polar

Dejar\(w = r(\cos(\alpha) + i\sin(\alpha))\) y\(z = s(\cos(\beta) + i\sin(\beta))\) ser números complejos en forma polar con\(z \neq 0\). Entonces

\[\dfrac{w}{z} = \dfrac{r(\cos(\alpha) + i\sin(\alpha))}{s(\cos(\beta) + i\sin(\beta)} = \dfrac{r}{s}\left [\dfrac{\cos(\alpha) + i\sin(\alpha)}{\cos(\beta) + i\sin(\beta)} \right ]\]

Trabajaremos con la fracción\(\dfrac{\cos(\alpha) + i\sin(\alpha)}{\cos(\beta) + i\sin(\beta)}\) y seguiremos la práctica habitual de multiplicar el numerador y denominador por\(\cos(\beta) - i\sin(\beta)\). Entonces

\[\dfrac{w}{z} = \dfrac{r}{s}\left [\dfrac{(\cos(\alpha) + i\sin(\alpha))}{(\cos(\beta) + i\sin(\beta)} \right ] = \dfrac{r}{s}\left [\dfrac{(\cos(\alpha) + i\sin(\alpha))}{(\cos(\beta) + i\sin(\beta)} \cdot \dfrac{(\cos(\beta) - i\sin(\beta))}{(\cos(\beta) - i\sin(\beta)} \right ] = \dfrac{r}{s}\left [\dfrac{(\cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta)) + i(\sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta)}{\cos^{2}(\beta) + \sin^{2}(\beta)} \right ]\]

Ahora usamos las siguientes identidades con la última ecuación:

• \(\cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta) = \cos(\alpha - \beta)\)
• \(\sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta) = \sin(\alpha - \beta)\)
• \(\cos^{2}(\beta) + \sin^{2}(\beta) = 1\)

Usando estas identidades con la última ecuación para\(\dfrac{w}{z}\), vemos que

\[\dfrac{w}{z} = \dfrac{r}{s}[\dfrac{\cos(\alpha - \beta) + i\sin(\alpha- \beta)}{1}].\]

Resumen

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

Si\(z = a + bi\) es un número complejo, entonces podemos trazar\(z\) en el plano. Si\(r\) es la magnitud de\(z\) (es decir, la distancia desde\(z\) el origen) y\(\theta\) el ángulo\(z\) hace con el eje real positivo, entonces la forma trigonométrica (o forma polar) de\(z\) is\(z = r(\cos(\theta) + i\sin(\theta))\), donde

\[r = \sqrt{a^{2} + b^{2}}, \cos(\theta) = \dfrac{a}{r}\]

y\[\sin(\theta) = \dfrac{b}{r}\]

El ángulo\(\theta\) se llama el argumento del número complejo\(z\) y el número real\(r\) es el módulo o norma de\(z\).

Si\(w = r(\cos(\alpha) + i\sin(\alpha))\) y\(z = s(\cos(\beta) + i\sin(\beta))\) son números complejos en forma polar, entonces la forma polar del producto complejo\(wz\) viene dada por

\[wz = rs(\cos(\alpha + \beta) + i\sin(\alpha + \beta))\]y\(z \neq 0\), la forma polar del cociente complejo\(\dfrac{w}{z}\) es

\[\dfrac{w}{z} = \dfrac{r}{s}(\cos(\alpha - \beta) + i\sin(\alpha - \beta)),\]

Esto establece que para multiplicar dos números complejos en forma polar, multiplicamos sus normas y sumamos sus argumentos, y para dividir dos números complejos, dividimos sus normas y restamos sus argumentos.