5.1: El sistema numérico complejo

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Qué es un número complejo?
• ¿Qué significa que dos números complejos sean iguales?
• ¿Cómo sumamos dos números complejos juntos?
• ¿Cómo multiplicamos dos números complejos juntos?
• ¿Cuál es el conjugado de un número complejo?
• ¿Cuál es el módulo de un número complejo?
• ¿Cómo se relacionan el conjugado y el módulo de un número complejo?
• ¿Cómo dividimos un número complejo por otro?

La fórmula cuadrática nos\(x = \dfrac{-b \pm \sqrt{b^{2} - 4ac}}{2a}\) permite encontrar soluciones a la ecuación cuadrática\(ax^2+ bx + c = 0\). Por ejemplo, las soluciones a la ecuación\(x^{2} + x + 1 = 0\) son

\[x = \dfrac{-1 \pm \sqrt{1 - 4}}{2} = \dfrac{-1 \pm \sqrt{-3}}{2}. \nonumber\]

Un problema surge de inmediato con esta solución ya que no hay número real\(t\) con el inmueble que\(t^{2} = -3\) o\(t = \sqrt{-3}\). Para dar sentido a soluciones como esta introducimos números complejos. Aunque los números complejos surgen naturalmente al resolver ecuaciones cuadráticas, su introducción en las matemáticas surgió del problema de resolver ecuaciones cúbicas.

Si usamos la fórmula cuadrática para resolver una ecuación como\(x^{2} + x + 1 = 0\),

obtenemos las soluciones\(x = \dfrac{-1 + \sqrt{-3}}{2}\) y\(x = \dfrac{-1 - \sqrt{-3}}{2}\). Estos números son números complejos y tenemos una forma especial para escribir estos números. Los escribimos de una manera que aísla la raíz cuadrada de\(-1\). Para ilustrar, el número

\[\dfrac{-1 + \sqrt{-3}}{2} \nonumber\]

se puede escribir de la siguiente manera:

\[\dfrac{-1 + \sqrt{-3}}{2} = -\dfrac{1}{2} + \dfrac{\sqrt{-3}}{2} = -\dfrac{1}{2} + \dfrac{\sqrt{3}\sqrt{-1}}{2} = -\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}\sqrt{-1} \nonumber\]

Dado que no hay un número real\(t\) satisfactorio\(t^{2} = -1\), el número no\(\sqrt{-1}\) es un número real. Llamamos a\(\sqrt{-1}\) un número imaginario y le damos una etiqueta especial\(i\). Así,\(i = \sqrt{-1}\) o\(i^{2} = -1\). Con esto en mente podemos escribir

\[\dfrac{-1 + \sqrt{-3}}{2} = -\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i \nonumber\]

y cada número complejo tiene esta forma especial.

Definición: Números Complejos

Un número complejo es un objeto de la forma

\[a + bi\]

donde\(a\) y\(b\) son los números reales y\(i^{2} = -1\).

La forma\(a + bi\), donde a y b son números reales se llama la forma estándar para un número complejo. Cuando tenemos un número complejo de la forma\(z = a + bi\), el número\(a\) se llama la parte real del número complejo\(z\) y el número\(b\) se llama la parte imaginaria de\(z\). Como i no es un número real, dos números complejos\(a + bi\) y\(c + di\) son iguales si y solo si\(a = c\) y\(b = d\).

Hay una aritmética de números complejos que está determinada por una suma y multiplicación de números complejos. Sumar y restar números complejos es natural:

\[(a + bi) + (c + di) = (a + c) + (b + d)i\]

\[(a + bi) - (c + di) = (a - c) + (b - d)i\]

Es decir, para sumar (o restar) dos números complejos sumamos (restamos) sus partes reales y sumamos (restamos) sus partes imaginarias. La multiplicación también se hace de manera natural —para multiplicar dos números complejos, simplemente expandimos el producto como de costumbre y explotamos el hecho de que\(i^{2} = -1\). Entonces el producto de dos números complejos es

\[\begin{align*} (a + bi) + (c + di) &= ac + (ad)i + (bc)i + (bd)i^{2} \\[4pt] &= (ac - bd) + (ad + bc)i \end{align*}\]

Propiedades de Número Complejo

Se puede demostrar que los números complejos satisfacen muchas propiedades útiles y familiares, que son similares a las propiedades de los números reales. Si\(u\),\(w\), y\(z\), son números complejos, entonces

1. \(w + z = z + w\)
2. \(u + (w + z) = (u + w) + z\)
3. El número complejo\(0 = 0 + 0i\) es una identidad aditiva, es decir\(z + 0 = z\).
4. Si\(z = a + bi\), entonces la inversa aditiva de\(z\) es\(-z = (-a) + (-b)i\). Es decir,\(z + (-z) = 0\).
5. \(wz = zw\)
6. \(u(wz) = (uw)z\)
7. \(u(w + z) = uw + uz\)
8. Si\(wz = 0\), entonces\(w = 0\) o\(z = 0\).

Utilizaremos estas propiedades según sea necesario. Por ejemplo, para escribir el producto complejo\((1 + i)i\) en la forma\(a + bi\) con\(a\) y números\(b\) reales, distribuimos la multiplicación sobre la suma y usamos el hecho de que\(i^{2} = -1\) para ver eso

\[(1 + i)i = i + i^{2} = i + (-1) = (-1) + i.\]

Para otro ejemplo, si\(w = 2 + i\) y\(z = 3 - 2i\), podemos usar estas propiedades para escribir\(wz\) en la\(a + bi\) forma estándar de la siguiente manera:

\[wz = (2 + i)z = 2z + iz = 2(3 - 2i) + i(3 - 2i) = (6 - 4i) + (3i - 2i^{2}) = 6 - 4i + 3i - 2(-1) = 8 - i\]

Ejercicio\(\PageIndex{1A}\)

Escribe cada una de las sumas o productos como un número complejo en forma estándar.

1. \((2 + 3i) + (7 - 4i)\)
2. \((4 - 2i)(3 + i)\)
3. \((2 + i)i - (3 + 4i)\)

Responder

a)\((2 + 3i) + (7 - 4i) = 9 - i\)

b)\((4 - 2i)(3 + i) = (4 - 2i)3 + (4 - 2i)i = 14 - 2i\)

c)\((2 + i)i - (3 + 4i) = (2i - 1) - 3 - 4i = -4 - 2i\)

Ejercicio\(\PageIndex{1B}\)

Utilice la fórmula cuadrática para escribir las dos soluciones a la ecuación cuadrática\(x^{2} - x +2 = 0\) como números complejos de la forma\(r + si\) y\(u + vi\) para algunos números reales\(r\),\(s\),\(u\), y\(v\).

(Pista: Recuerda:\(i = \sqrt{-1}\). Para que podamos reescribir algo como\(\sqrt{-4}\) as\(\sqrt{-4} = \sqrt{4}\sqrt{-1} = 2i\).)

Responder

Utilizamos la fórmula cuadrática para resolver la ecuación y obtener\[x = \dfrac{1 \pm \sqrt{-7}}{2}.\]

Entonces podemos escribir\(\sqrt{-7} = i\sqrt{7}\). Entonces las dos soluciones de la ecuación cuadrática son:

\[\begin{align*} x &= \dfrac{1 \pm i\sqrt{7}}{2} \\[4pt] &= \dfrac{1}{2} \pm \dfrac{\sqrt{7}}{2}i \\[4pt] \end{align*}\]

División de Números Complejos

Podemos sumar, restar y multiplicar números complejos, por lo que es natural preguntar si podemos dividir números complejos. Ilustramos con un ejemplo.

Ejemplo\(\PageIndex{2}\): Dividing by a Complex Number

Escribe el cociente\(\dfrac{2 + i}{3 + i}\) como un número complejo en el formulario\(a + bi\).

Solución

Este problema es racionalizar un denominador desde entonces\(i = \sqrt{-1}\). Entonces en este caso necesitamos “quitar” la parte imaginaria del denominador. Recordemos que el producto de un número complejo con su conjugado es un número real, así que si multiplicamos el numerador y denominador de\(\dfrac{2 + i}{3 + i}\) por el conjugado complejo del denominador, podemos reescribir el denominador como un número real. Los pasos son los siguientes. Multiplicando el numerador y denominador por el conjugado\(3 - i\) o nos\(3 + i\) da

\[\dfrac{2 + i}{3 + i} = \left(\dfrac{2 + i}{3 + i}\right)\left(\dfrac{3 - i}{3 - i}\right) = \dfrac{(2 + i)(3 - i)}{(3 + i)(3 - i)} = \dfrac{(6 - i^{2}) + (-2 + 3)i}{9 - i^{2}} = \dfrac{7 + i}{10} \nonumber\]

Ahora podemos escribir el resultado final en forma estándar como

\[\dfrac{7 + i}{10} = \dfrac{7}{10} + \dfrac{1}{10}i. \nonumber\]

Ejemplo\(\PageIndex{2}\) ilustra el proceso general para dividir un número complejo por otro. En general, podemos escribir el cociente\(\dfrac{a + bi}{c + di}\) en la forma\(r + si\) multiplicando el numerador y denominador de nuestra fracción por el conjugado\(c - di\) de\(c + di\) para ver que

\[\dfrac{a + bi}{c + di} = \left(\dfrac{a + bi}{c + di}\right)\left(\dfrac{c - di}{c - di}\right) = \dfrac{(ac + bd) + (bc - ad)i}{c^{2} + d^{2}} = \dfrac{ac + bd}{c^{2} + d^{2}} + \dfrac{bc - ad}{c^{2} + d^{2}}i\]

Por lo tanto, tenemos la fórmula para el cociente de dos números complejos.

Definición: Cociente de números complejos

El cociente\(\dfrac{a + bi}{c + di}\) de los números complejos\(a + bi\) y\(c + di\) es el número complejo

\[\dfrac{a + bi}{c + di} = \dfrac{ac + bd}{c^{2} + d^{2}} + \dfrac{bc - ad}{c^{2} + d^{2}}i\]

siempre\(c + di \neq 0\).

Ejercicio\(\PageIndex{3}\)

Dejar\(z = 3 + 4i\) y\(w = 5 - i\).

1. Escribe\(\dfrac{w}{z} = \dfrac{5 - i}{3 + 4i}\) como un número complejo en la forma\(r + si\) donde\(r\) y\(s\) son algunos números reales. Verifique el resultado multiplicando el cociente por\(3 + 4i\). ¿Este producto es igual a\(5 - i\)?
2. Encuentra la solución a la ecuación\((3 + 4i)x = 5 - i\) como un número complejo en la forma\(x = u + vi\) donde\(u\) y\(v\) son algunos números reales.

Responder

1. Usando nuestra fórmula con\(a = 5, b = -1, c = 3\) y nos\(d = 4\) da\[\dfrac{5 - i}{3 + 4i} = \dfrac{15 - 4}{15} + \dfrac{-3 -20}{25}i = \dfrac{11}{25} - \dfrac{23}{25}i\] Como cheque, vemos que\[\left(\dfrac{11}{25} - \dfrac{23}{25}i\right)\left(3 + 4i\right) = \left(\dfrac{33}{25} - \dfrac{69}{25}i\right) + \dfrac{44}{25}i - \dfrac{92}{25}i^{2} = \left(\dfrac{33}{25} + \dfrac{92}{25}\right) + \left(-\dfrac{69}{25}i + \dfrac{44}{25}i\right) = 5 - i\]
2. Podemos resolver\(x\) por dividiendo ambos lados de la ecuación por\(3 + 4i\) ver que\[x = \dfrac{5 - i}{3 + 4i} = \dfrac{11}{25} - \dfrac{23}{25}i\]

Representaciones geométricas de números complejos

Cada par ordenado\((a , b)\) de números reales determina:

• Un punto en el plano de coordenadas con coordenadas\((a , b)\).
• Un número complejo\(a + bi\)
• Un vector\(a\textbf{i} + b\textbf{j} = ( a, b )\)

Esto significa que podemos representar geométricamente el número complejo\(a + bi\) con un vector en posición estándar con punto terminal\((a , b)\). Por lo tanto, podemos dibujar imágenes de números complejos en el plano. Cuando hacemos esto, el eje horizontal se llama eje real, y el eje vertical se llama eje imaginario. Además, el plano de coordenadas se denomina entonces plano complejo. Es decir, si\(z = a + b i\), podemos pensar\(z\) como un segmento lineal dirigido desde el origen hasta el punto (a, b), donde el punto terminal del segmento son\(a\) unidades del eje imaginario y\(b\) unidades del eje real. Por ejemplo, los números complejos\(3 + 4i\) y\(-8 + 3i\) se muestran en la Figura 5.1.

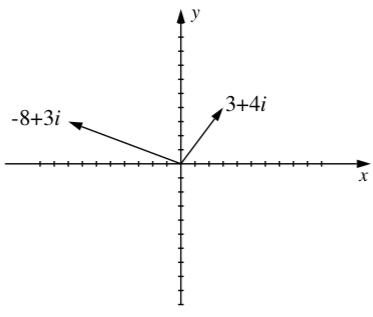
Figura\(\PageIndex{1}\): Dos números complejos.

Además, la suma de dos números complejos se puede representar geométricamente usando las formas vectoriales de los números complejos. Dibuja el paralelogramo definido por\(w = a + bi\) y\(z = c + di\). La suma de\(w\) y\(z\) es el número complejo representado por el vector desde el origen hasta el vértice en el paralelogramo opuesto al origen como se ilustra con los vectores\(w = 3 + 4i\) y\(z = -8 + 3i\) en la Figura\(\PageIndex{2}\).

Ejercicio\(\PageIndex{4}\)

Dejar\(w = 2 + 3i\) y\(z = -1 + 5i\).

1. Escribe la suma compleja\(w + z\) en forma estándar.
2. Dibuja una imagen para ilustrar la suma usando vectores para representar\(w\) y\(z\).

Responder

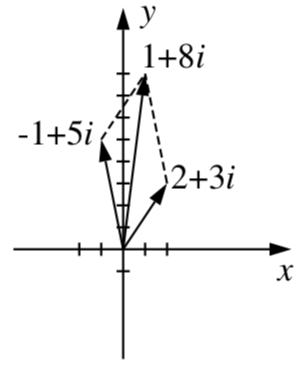
1. La suma es\(w + z = (2 - 1) + (3 + 5)i = 1 + 8i\).

2. En la siguiente figura se muestra una representación de la suma compleja usando vectores.

Ahora ampliamos nuestro uso de la representación de un número complejo como vector en posición estándar para incluir la noción de la longitud de un vector. Recordemos de la Sección 3.6 que la longitud de un vector\(\textbf{v} = a\textbf{i} + b\textbf{j}\) es\(|\textbf{v}| = \sqrt{a^{2} + b^{2}}\).

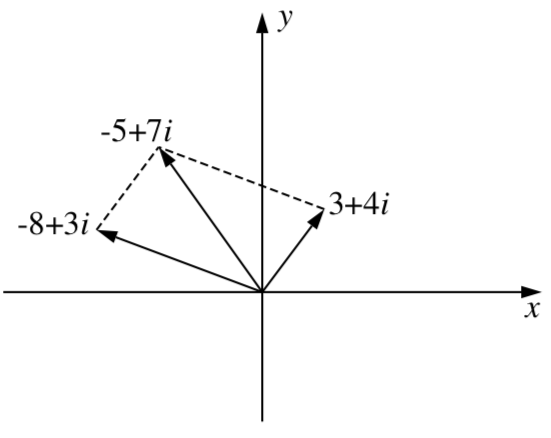
Figura\(\PageIndex{2}\): La suma de dos números complejos.

Cuando usamos esta idea con números complejos, la llamamos la norma o módulo del número complejo.

Definición: Norma

La norma (o módulo) del número complejo\(z = a + bi\) es la distancia desde el origen hasta el punto\((a, b)\) y se denota por\(|z|\). Vemos

que\[|z| = |a + bi| = \sqrt{a^{2} + b^{2}}.\]

Hay otro concepto relacionado con el número complejo que se basa en el siguiente bit de álgebra.

\[(a + bi)(a -bi) = a^{2} - (bi)^{2} = a^{2} - b^{2}i^{2} = a^{2} + b^{2}\]

El número complejo\(a - bi\) se llama el conjugado complejo de\(a + bi\). Si lo dejamos\(z = a + bi\), denotamos el complejo conjugado de\(z\) as\(\bar{z}\). Entonces\[\bar{z} = \overline{a + bi} = a - bi.\]

También notamos que

\[z\bar{z} = (a + bi)(a - bi) = a^{2} + b^{2},\]

y así el producto de un número complejo con su conjugado es un número real. De hecho,

\[z\bar{z} = a^{2} + b^{2} = |z|^{2},\], y así\[|z| = \sqrt{z\bar{z}}\]

Ejercicio\(\PageIndex{5}\)

Let\(w = 2 + 3i\) y\(z = -1 + 5i\)

1. Encontrar\(\bar{w}\) y\(\bar{z}\).
2. Cómputos\(|w|\) y\(|z|\).
3. Cómputos\(w\bar{w}\) y\(z\bar{z}\).
4. ¿Qué es\(\bar{z}\) si\(z\) es un número real?

Responder

1. Usando la definición del conjugado de un número complejo encontramos que\(\bar{w} = 2 - 3i\) y\(\bar{z} = -1 - 5i\).
2. Utilizando la definición de la norma de un número complejo nos encontramos con que\(|w| = \sqrt{2^{2} + 3^{2}} = \sqrt{13}\) y\(|z| = \sqrt{(-1)^{2} + 5^{2}} = \sqrt{26}\).
3. Usando la definición del producto de números complejos encontramos que

\[w\bar{w} = (2 + 3i)(2 - 3i) = 4 + 9 = 13\]

\[z\bar{z} = (-1 + 5i)(-1 - 5i) = 1 + 25 = 26\]

4. Vamos\(z = a + 0i\) para algunos\(a \in \mathbb{R}\). Entonces\(\bar{z} = a - 0i\). Así,\(\bar{z} = z\) cuando\(z \in \mathbb{R}\).

Resumen

En esta sección, estudiamos los siguientes conceptos e ideas importantes:

• Un número complejo es un objeto de la forma\(a + bi\), donde\(a\) y\(b\) son números reales y\(i^{2} = -1\). Cuando tenemos un número complejo de la forma\(z = a + bi\), el número\(a\) se llama la parte real del número complejo\(z\) y el número\(b\) se llama la parte imaginaria de\(z\).
• Podemos sumar, restar, multiplicar y dividir números complejos de la siguiente manera:

\[(a + bi) + (c + di) = (a + c) + (b + d)i \nonumber \]

\[(a + bi) - (c + di) = (a - c) + (b - d)i\nonumber\]

\[(a + bi)(c + di) = (ac - bd) + (ad + bc)i\nonumber\]

\[\dfrac{a + bi}{c + di} = \dfrac{ac + bd}{c^{2} + d^{2}} + \dfrac{bc - ad}{c^{2} + d^{2}}i\nonumber\]siempre\(c + di \neq 0\)

• Un número complejo se\(a + bi\) puede representar geométricamente con un vector en posición estándar con punto terminal\((a, b)\). Cuando hacemos esto, el eje horizontal se llama eje real, y el eje vertical se llama eje imaginario. Además, el plano de coordenadas se denomina entonces plano complejo. Es decir, si\(z = a + bi\) podemos pensar en un segmento lineal dirigido desde el origen hasta el punto\((a, b)\), donde el punto terminal del segmento es una unidad del eje imaginario y\(b\) unidades del eje real.\(z\)
• La norma (o módulo) del número complejo\(z = a + bi\) es la distancia desde el origen hasta el punto\((a, b)\) y se denota por\(|z|\). Vemos que\[|z| = |a + bi| = \sqrt{a^{2} + b^{2}} \nonumber\]
• El número complejo\(a - bi\) se llama el conjugado complejo de\(a + bi\). Tenga en cuenta que\[(a + bi)(a - bi) = a^{2} + b^{2} = |a + bi|^{2} \nonumber\]