5.4: El sistema de coordenadas polares

Última actualización
Guardar como PDF

Page ID: 113371

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

¿Cómo se determinan las coordenadas polares de un punto en el plano?
¿Cómo convertimos de coordenadas polares a coordenadas rectangulares?
¿Cómo convertimos de coordenadas rectangulares a polares?
¿Cómo podemos graficar correctamente las ecuaciones polares tanto a mano como con una calculadora?

Actividad inicial

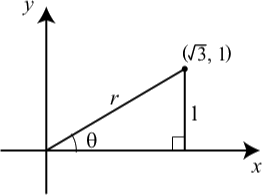
En el diagrama se$(\sqrt{3}, 1)$ ha trazado el punto con coordenadas. Determinar el valor de$r$ y el ángulo$\theta$ en radianes y grados.

$imageedit_2_7600796155.png$

En nuestro estudio de la trigonometría hasta el momento, siempre que graficamos una ecuación o ubicamos un punto en el plano, hemos utilizado coordenadas rectangulares (o cartesianas). El uso de este tipo de sistema de coordenadas revolucionó las matemáticas ya que proporcionó el primer vínculo sistemático entre geometría y álgebra. Aunque el sistema de coordenadas rectangulares es muy importante, existen otros métodos para ubicar puntos en el plano. Estudiaremos uno de esos sistemas en esta sección.

Las coordenadas rectangulares utilizan dos números (en forma de par ordenado) para determinar la ubicación de un punto en el plano. Estos números dan la posición de un punto que corresponde al par ordenado$(\sqrt{3}, 1)$, partimos en el origen y viajamos$\sqrt{3}$ unidades a la derecha y luego viajamos$1$ unidad hacia arriba. La idea del sistema de coordenadas polares es dar una distancia a recorrer y un ángulo en qué dirección viajar. Llegamos al mismo punto que el dado por las coordenadas$(\sqrt{3}, 1)$ rectangulares diciendo que viajaremos 2 unidades en un ángulo de$30^\circ$ desde el$x$ eje -eje. Estos valores corresponden a los valores de$r$ y$\theta$ en el diagrama para la actividad inicial. Usando el Teorema de Pitágoras, podemos obtener$r = 2$ y utilizando el hecho de que$\sin(\theta) = \dfrac{1}{2}$, vemos que$\theta = \dfrac{\pi}{6}$ radianes o$30^\circ$.

El sistema de coordenadas polares

Para el sistema de coordenadas rectangulares, utilizamos dos números, en forma de par ordenado, para ubicar un punto en el plano. Hacemos lo mismo para las coordenadas polares, pero ahora el primer número representa una distancia desde un punto y el segundo número representa un ángulo. En el sistema de coordenadas polares, comenzamos con un punto$O$, llamado polo y a partir de este punto, dibujamos un rayo horizontal (media línea dirigida) llamado eje polar. Luego podemos asignar coordenadas polares$r, \theta$ a un punto$P$ en el plano de la siguiente manera (ver Figura 5.5):

El número$r$, llamado distancia radial, es la distancia dirigida desde el polo hasta el punto$P$.
El número$\theta$, llamado ángulo polar, es la medida del ángulo desde el eje polar hasta el segmento lineal$OP$. (Se pueden usar radianes o grados para la medida del ángulo).

Convenciones para coordenadas polares

El ángulo polar$\theta$ se considera positivo si se mide en sentido contrario a las agujas del reloj desde el eje polar.

El ángulo polar$\theta$ se considera negativo si se mide en sentido horario desde el eje polar.

Si la distancia radial$r$ es positiva, entonces el punto$P$ es$r$ unidades$O$ a lo largo del lado terminal de$\theta$.

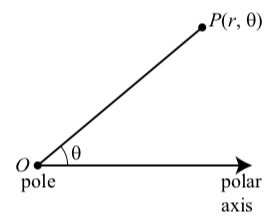
$5.5.png$

Figura$\PageIndex{1}$: Coordenadas polares

Si la distancia radial$r$ es negativa, entonces el punto$P$ es$|r$ unidades$O$ a lo largo del rayo en la dirección opuesta a la del lado terminal de$\theta$.
Si la distancia radial$r$ es cero, entonces el punto$P$ es el punto$O$.

Para ilustrar algunas de estas convenciones, considere el punto$P(3, \dfrac{4\pi}{3})$ mostrado a la izquierda en la Figura$\PageIndex{2}$. (Observe que se ha dibujado el círculo de radio$3$ con centro en el polo).

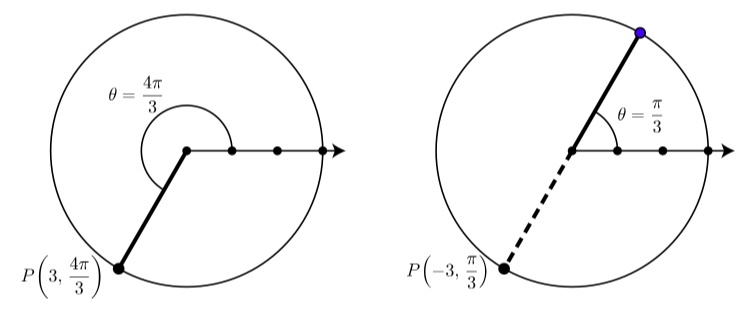
$5.6.png$

Figura$\PageIndex{2}$: Un punto con dos conjuntos diferentes de coordenadas polares

El diagrama de la derecha en la Figura$\PageIndex{2}$ ilustra que este punto$P$ también tiene coordenadas polares$P(-3, \dfrac{\pi}{3})$. Esto se debe a que cuando usamos el ángulo polar$\theta = \dfrac{\pi}{3}$ y la distancia radial$r = -3$, entonces el punto$P$ es$3$ unidades del polo a lo largo del rayo en la dirección opuesta como el lado terminal de$\theta$.

Ejercicio$\PageIndex{1}$

Dado que un punto con coordenadas polares$(r, \theta)$ debe estar en un círculo de radio r con centro en el polo, es razonable ubicar puntos en una cuadrícula de círculos concéntricos y rayos cuyo punto inicial está en el polo como se muestra en la Figura$\PageIndex{3}$. En este papel cuadrificado polar, cada incremento de ángulo es$\dfrac{\pi}{12}$ radianes. Por ejemplo, el punto$(4, \dfrac{\pi}{6})$ se traza en la Figura$\PageIndex{3}$.

$imageedit_5_9713579129.png$

Figura$\PageIndex{3}$: Papel cuadricular polar

Trace los siguientes puntos con las coordenadas polares especificadas.

\[(1, \dfrac{\pi}{4}), (5, \dfrac{\pi}{4}), (2, \dfrac{\pi}{3}), (3, \dfrac{5\pi}{4}), (4, -\dfrac{\pi}{4}), (4, \dfrac{7\pi}{4}), (6, \dfrac{5\pi}{6}), (5, \dfrac{9\pi}{4}), (-5, \dfrac{5\pi}{4})\]

Contestar: $imageedit_15_7821453481.png$

En Ejercicio$\PageIndex{1}$, notamos que las coordenadas polares$(5, \dfrac{\pi}{4}), (5, \dfrac{9\pi}{4})$, y$(-5, \dfrac{5\pi}{4})$ todas determinaron el mismo punto en el plano. Esto ilustra una diferencia importante entre las coordenadas rectangulares y las coordenadas polares. Mientras que cada punto tiene una representación única en coordenadas rectangulares, un punto dado puede tener muchas representaciones diferentes en coordenadas polares. Esto se debe principalmente a que el sistema de coordenadas polares utiliza círculos concéntricos para su cuadrícula, y podemos comenzar en un punto en un círculo y viajar alrededor del círculo y terminar en el punto desde el que partimos. Ya que una envoltura alrededor de un círculo corresponde a un ángulo de$2\pi$ radianes o$360^\circ$, tenemos lo siguiente:

Coordenadas polares de un punto

Un punto$P$, distinto del polo, determinado por las coordenadas polares también$(r, \theta)$ está determinado por las siguientes coordenadas polares:

En radianes:

\[(r, \theta + k(2\pi))\]\[(-r, \theta + (2k + 1)\pi)\]

En grados:

\[(r, \theta + k(360^\circ))\]\[(-r, \theta + (2k + 1)180^\circ)\]

donde$k$ puede ser cualquier entero.
Si el punto$P$ es el polo, sus coordenadas polares son$(0, \theta)$ para cualquier ángulo polar$\theta$.

Ejercicio$\PageIndex{2}$

Encuentra cuatro representaciones diferentes en coordenadas polares para el punto con coordenadas polares$(3, 110^\circ)$. Utilice un valor positivo para la distancia radial$r$ para dos de las representaciones y un valor negativo para la distancia radial$r$ para las otras dos representaciones.

Contestar

La columna izquierda muestra algunos conjuntos de coordenadas polares con un valor positivo para$r$ y la columna derecha muestra algunos conjuntos de coordenadas polares con un valor negativo para$r$.

\[(3, 470^\circ)\]

\[(-3, 290^\circ)\]

\[(3, 830^\circ)\]

\[(-3, 650^\circ)\]

\[(3, -250^\circ)\]

\[(-3, -70^\circ)\]

\[(3, -510^\circ)\]

\[(-3, -430^\circ)\]

\[(3, 1190^\circ)\]

\[(-3, 1010^\circ)\]

Conversiones entre coordenadas polares y rectangulares

Ahora tenemos dos formas de localizar puntos en el avión. Uno es el habitual sistema de coordenadas rectangulares (cartesianas) y el otro es el sistema de coordenadas polares. El sistema de coordenadas rectangulares utiliza dos distancias para ubicar un punto, mientras que el sistema de coordenadas polares utiliza una distancia y un ángulo para ubicar un punto. Si bien estos dos sistemas se pueden estudiar independientemente uno del otro, podemos configurarlos para que exista una relación entre los dos tipos de coordenadas. Hacemos esto de la siguiente manera:

Colocamos el polo del sistema de coordenadas polares en el origen del sistema de coordenadas rectangulares.
Tenemos el eje polar del sistema de coordenadas polares coincidiendo con el$x$ eje positivo del sistema de coordenadas rectangulares como se muestra en la Figura$\PageIndex{4}$

Utilizando la trigonometría del triángulo rectángulo y el Teorema de Pitágoras, obtenemos las siguientes relaciones entre las coordenadas rectangulares$(x, y)$ y las coordenadas polares$(r, \theta)$:

\[\cos(\theta) = \dfrac{x}{r}\]\[x = r\cos(\theta)\]

\[\sin(\theta) = \dfrac{y}{r}\]\[y = r\sin(\theta)\]

\[\tan(\theta) = \dfrac{y}{x}\]si$x \neq 0$\[x^{2} + y^{2} = r^{2}\]

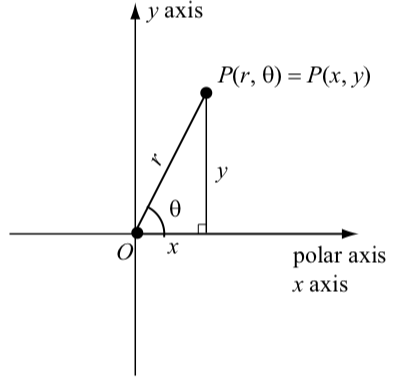
$5.8.png$

Figura$\PageIndex{4}$: Coordenadas polares y rectangulares

Conversión de coordenadas

Para determinar las coordenadas rectangulares$(x, y)$ de un punto cuyas coordenadas polares$(r, \theta)$ son conocidas, utilice las ecuaciones

\[x = r\cos(\theta)\]\[y = r\sin(\theta)\]

Para determinar las coordenadas polares$(r, \theta)$ de un punto cuyas coordenadas rectangulares$(x, y)$ son conocidas, utilice la ecuación$r^{2} = x^{2} + y^{2}$ para determinar$r$ y determinar un ángulo de$\theta$ manera que

\[\tan(\theta) = \dfrac{y}{x}\]si$x \neq 0$

\[\cos(\theta) = \dfrac{x}{r}\]

\[\sin(\theta) = \dfrac{y}{r}\]

Al determinar las coordenadas polares de un punto, generalmente elegimos el valor positivo para$r$. Podemos usar una función trigonométrica inversa para ayudar a determinar$\theta$ pero debemos tener cuidado de colocarlo$\theta$ en el cuadrante apropiado usando los signos de$x$ y$y$. Tenga en cuenta que si$x = 0$, podemos usar$\theta = \dfrac{\pi}{2}$ o$\theta = \dfrac{3\pi}{2}$

Ejercicio$\PageIndex{3}$

Determine las coordenadas rectangulares para cada uno de los siguientes puntos en coordenadas polares:

\[(3, \dfrac{\pi}{3})\]\[(5, \dfrac{11\pi}{6})\]\[(-5, \dfrac{3\pi}{4})\]

Cuando convertimos de coordenadas rectangulares a coordenadas polares, debemos tener cuidado y usar los signos de$x$ y$y$ determinar el cuadrante adecuado para el ángulo$\theta$. En muchas situaciones, podría ser más fácil determinar primero el ángulo de referencia para el ángulo$\theta$ y luego usar los signos de$x$ y$y$ determinar$\theta$.

Contestar

Para cada punto, utilizamos las ecuaciones$x = r\cos(\theta)$ y$y = r\sin(\theta)$. En cada uno de estos casos, podemos determinar los valores exactos para$x$ y$y$.

	Coordenadas polares	Coordenadas rectangulares
1.	$(3, \dfrac{\pi}{3})$	$(\dfrac{3}{2}, \dfrac{3\sqrt{3}}{2})$
2.	$(5, \dfrac{11\pi}{6})$	$(\dfrac{5\sqrt{3}}{2}, -\dfrac{5}{2})$
3.	$(-5, \dfrac{3\pi}{4})$	$(\dfrac{5\sqrt{2}}{2}, -\dfrac{5\sqrt{2}}{2})$

Ejemplo$\PageIndex{1}$: (Converting from Rectangular to Polar Coordinates)

Para determinar las coordenadas polares para el punto$(-2, 2)$ en coordenadas rectangulares, primero dibujamos una imagen y notamos que

\[r^{2} = (-2)^{2} + 2^{2} = 8 \nonumber\]

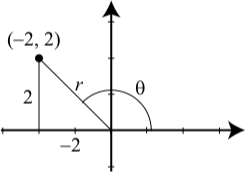
$imageedit_9_6159139972.png$

Ya que suele ser más fácil trabajar con un valor positivo para$r$, vamos a utilizar$r = \sqrt{8}$.

Eso también lo vemos$\tan(\theta) = \dfrac{3}{-3} = -1$. Podemos usar muchos valores diferentes para$\theta$ pero para mantenerlo fácil, usamos$\theta$ como se muestra en el diagrama. Para el ángulo de referencia$\hat{\theta}$, tenemos$\tan(\hat{\theta}) = 1$ y así$\hat{\theta} = \dfrac{\pi}{4}$. Desde$-2 < 0$ y$2 > 0$,$\theta$ está en el segundo cuadrante, y tenemos\[\theta = \pi - \dfrac{\pi}{4} = \dfrac{3\pi}{4}\]

Entonces el punto$(-2, 2)$ en coordenadas rectangulares tiene coordenadas polares$(\sqrt{8}, \dfrac{3\pi}{4})$.

Ejercicio$\PageIndex{4}$

Determine las coordenadas polares para cada uno de los siguientes puntos en coordenadas rectangulares:

\[(6, 6\sqrt{3})\]\[(0, -4)\]\[(-4, 5)\]

En cada caso, use una distancia radial positiva$r$ y un ángulo polar$\theta$ con$0 \leq \theta \leq 2\pi$.

Se necesitará utilizar una función trigonométrica inversa para (3).

Contestar

1. Para el punto$(6, 6\sqrt{3}), r^{2} = 6^{2} + (6\sqrt{3})^{2} = 144$ y así$r = 12$. Ya que el punto está en el primer cuadrante, podemos usar$\tan(\theta) = \sqrt{3}$ o$\cos(\theta) = \dfrac{1}{2}$ para concluir eso$\theta = \dfrac{\pi}{3}$. Entonces las coordenadas polares son$(12, \dfrac{\pi}{3})$.

2. Para el punto$(0, -4)$,$r^{2} = 0^{2} + (-4)^{2} = 16$ y así$r = 4$. Dado que el punto está en el$y$ eje -podemos usar$\cos(\theta) = 0$ y$\sin(\theta) - 1$ para concluir eso$\theta = \dfrac{3\pi}{2}$. Entonces las coordenadas polares son$(4, \dfrac{3\pi}{2})$.

3. Para el punto$(-4, 5\sqrt{3}), r^{2} = (-4)^{2} + 5^{2} = 41$ y así$r = \sqrt{41}$. Dado que el punto está en el segundo cuadrante, podemos utilizar$\tan(\theta) = -1.25$ para concluir que el ángulo de referencia es$\hat{\theta} = \tan^{-1}(-1.25)$. No podemos determinar un valor exacto para$\theta$ y así podemos decir que las coordenadas polares son$(\sqrt{41}, \pi - \tan^{-1}(1.25))$. También podemos aproximar el ángulo y ver que las coordenadas polares aproximadas son$(\sqrt{41}, 2.24554)$. Nota: Hay otras formas de escribir el ángulo$\theta$. Es cierto que$\theta = \pi - \cos^{-1}(\dfrac{4}{\sqrt{21}}) = \cos^{-1}(\dfrac{-4}{\sqrt{21}})$.

La Gráfica de una Ecuación Polar

La gráfica una ecuación en el sistema de coordenadas rectangulares consiste en todos los puntos$(x, y)$ que satisfacen la ecuación. La ecuación a menudo se puede escribir en forma de una función como$y = f(x)$ En este caso, un punto$(a, b)$ está en la gráfica de esta función si y sólo si$b = f(a)$ De manera similar,

Definición

Una ecuación cuyas variables son coordenadas polares (usualmente$r$ y$\theta$) se denomina ecuación polar. La gráfica de una ecuación polar es el conjunto de todos los puntos cuyas coordenadas polares$(r, \theta)$ satisfacen la ecuación dada.

Un ejemplo de una ecuación polar es$r = 4\sin(\theta)$. Para esta ecuación, observe que

Si$\theta = 0$, entonces$r = 4\sin(0) = 0$ y así el punto$(0, 0)$ (en coordenadas polares) está en la gráfica de esta ecuación.
Si$\theta = \dfrac{\pi}{6}$, entonces$r = 4\sin(\dfrac{\pi}{6}) = 4\cdot \dfrac{1}{2} = 2$ y así$(2, \dfrac{\pi}{6})$ está en la gráfica de esta ecuación. (Recuerde: para las coordenadas polares, el valor de$r$ es la primera coordenada.)

El método más básico para dibujar la gráfica de una ecuación polar es trazar los puntos que satisfacen la ecuación polar en papel cuadriculado polar como se muestra en la Figura$\PageIndex{4}$ y luego conectar los puntos con una curva suave.

Ejercicio$\PageIndex{5}$

En la siguiente tabla se muestran los valores de$r$ y$\theta$ para los puntos que están en la gráfica de la ecuación polar$r = 4\sin(\theta)$.

$r = 4\sin(\theta)$	$\theta$
\ (r = 4\ sin (\ theta)\) ">0	\ (\ theta\) ">0
\ (r = 4\ sin (\ theta)\) ">2	\ (\ theta\) ">$\dfrac{\pi}{6}$
\ (r = 4\ sin (\ theta)\) ">$2\sqrt{2}$	\ (\ theta\) ">$\dfrac{\pi}{4}$
\ (r = 4\ sin (\ theta)\) ">$2\sqrt{3}$	\ (\ theta\) ">$\dfrac{\pi}{3}$
\ (r = 4\ sin (\ theta)\) ">4	\ (\ theta\) ">$\dfrac{\pi}{2}$
\ (r = 4\ sin (\ theta)\) ">$2\sqrt{3}$	\ (\ theta\) ">$\dfrac{2\pi}{3}$
\ (r = 4\ sin (\ theta)\) ">$2\sqrt{2}$	\ (\ theta\) ">$\dfrac{3\pi}{4}$
\ (r = 4\ sin (\ theta)\) ">2	\ (\ theta\) ">$\dfrac{5\pi}{6}$
\ (r = 4\ sin (\ theta)\) ">0	\ (\ theta\) ">$\pi$

Trace estos puntos en papel cuadriculado polar y dibuje una curva suave a través de los puntos para la gráfica de la ecuación$r = 4\sin(\theta)$.

$imageedit_12_9615052837.png$

Contestar: $imageedit_18_3781089603.png$

Dependiendo de cuán cuidadosamente trazemos los puntos y qué tan bien dibujemos la curva, la gráfica en Ejercicio$\PageIndex{5}$ podría ser un círculo. Podemos, por supuesto, trazar más puntos. De hecho, en Ejercicio$\PageIndex{5}$, solo usamos valores para$\theta$ con$0 \leq \theta \leq \pi$. En la siguiente tabla se muestran los valores de$r$ y$\theta$ para los puntos que están en la gráfica de la ecuación polar$r = 4\sin(\theta)$ con$\pi \leq \theta \leq 2\pi$.

$r = 4\sin(\theta)$	$\theta$
\ (r = 4\ sin (\ theta)\) ">0	\ (\ theta\) ">$\pi$
\ (r = 4\ sin (\ theta)\) ">-2	\ (\ theta\) ">$\dfrac{7\pi}{6}$
\ (r = 4\ sin (\ theta)\) ">$-2\sqrt{2}$	\ (\ theta\) ">$\dfrac{5\pi}{4}$
\ (r = 4\ sin (\ theta)\) ">$-2\sqrt{3}$	\ (\ theta\) ">$\dfrac{4\pi}{3}$
\ (r = 4\ sin (\ theta)\) ">-4	\ (\ theta\) ">$\dfrac{3\pi}{2}$
\ (r = 4\ sin (\ theta)\) ">$-2\sqrt{3}$	\ (\ theta\) ">$\dfrac{5\pi}{3}$
\ (r = 4\ sin (\ theta)\) ">$-2\sqrt{2}$	\ (\ theta\) ">$\dfrac{7\pi}{4}$
\ (r = 4\ sin (\ theta)\) ">-2	\ (\ theta\) ">$\dfrac{11\pi}{6}$
\ (r = 4\ sin (\ theta)\) ">0	\ (\ theta\) ">$\pi$

Debido a los valores negativos para$r$, si trazamos estos puntos, obtendremos los mismos puntos que hicimos en Ejercicio$\PageIndex{4}$. Entonces, una buena pregunta para hacer es: “¿Realmente estos puntos se encuentran en un círculo?” Podemos responder a esta pregunta convirtiendo la ecuación$r = 4\sin(\theta)$ en una ecuación equivalente con coordenadas rectangulares.

Transformar una ecuación de forma polar a forma rectangular

Las fórmulas que utilizamos para convertir un punto en coordenadas polares en coordenadas rectangulares también se pueden utilizar para convertir una ecuación en forma polar a forma rectangular. Estas ecuaciones se dan en el recuadro de la página 326. Entonces veamos la ecuación$r = 4\sin(\theta)$ del Ejercicio$\PageIndex{5}$.

Ejercicio$\PageIndex{6}$

Empezamos con la ecuación$r = 4\sin(\theta)$. Queremos transformar esto en una ecuación que involucre$x$ y$y$. Ya que$r^{2} = x^{2} + y^{2}$, podría ser más fácil trabajar con$r^{2}$ en lugar de$r$.

Multiplique ambos lados de la ecuación$r = 4\sin(\theta)$ por$r$.
Ahora usa las ecuaciones$r^{2} = x^{2} + y^{2}$ para obtener una ecuación equivalente en$x$ y$y$.

Contestar

1. $r^{2} = 4r\sin(\theta)$

2. $x^{2} + y^{2} = 4y$

La gráfica de la ecuación de la gráfica$r = 4\sin(\theta)$ en coordenadas polares será la misma que la gráfica de$x^{2} + y^{2} = 4y$ en coordenadas rectangulares. Ahora podemos usar algo de álgebra de cursos previos de matemáticas para demostrar que esta es la gráfica de un círculo. La idea es recopilar todos los términos en el lado izquierdo de la ecuación y usar completar el cuadrado para los términos que involucran$y$.

Como recordatorio, si tenemos la expresión$t^{2} + at = 0$, completamos el cuadrado sumando$(\dfrac{a}{2})^{2}$ a ambos lados de la ecuación. Entonces tendremos un cuadrado perfecto en el lado izquierdo de la ecuación.

\[t^{2} + at + (\dfrac{a}{2})^{2} = (\dfrac{a}{2})^{2}\]

\[t^{2} + at + \dfrac{a^{2}}{4} = \dfrac{a^{2}}{4}\]

\[(t + \dfrac{a}{2})^ {2} = \dfrac{a^{2}}{4}\]

Entonces, para la ecuación$x^{2} + y^{2} = 4y$, tenemos

\[x^{2} + y^{2} - 4y = 0\]

\[x^{2} + y^{2} 4y + 4 = 4\]

\[x^{2} + (y - 2)^{2} = 2^{2}\]

Esta es la ecuación (en coordenadas rectangulares) de un círculo con radio$2$ y centro en el punto$(0, 2)$. Vemos que esto es consistente con la gráfica que obtuvimos en Ejercicio$\PageIndex{5}$.

Ejercicio$\PageIndex{7}$

Transformar la ecuación$r = 6\cos(\theta)$ en una ecuación en coordenadas rectangulares y luego explicar por qué la gráfica de$r = 6\cos(\theta)$ es un círculo. ¿Cuál es el radio de este círculo y cuál es su centro?

Contestar

\[r^{2} = 6r\sin(\theta), x^{2} + y^{2} = 6x\]

\[x^{2} - 6x + 9 + y^{2} = 9, (x - 3)^{2} + y^{2} = 3^{2}\]

Entonces la gráfica de$r = 3\cos(\theta)$ es un círculo con radio$3$ y centro en$(3, 0)$.

La rejilla polar

Presentamos el papel cuadrificado polar en la Figura 5.7. Observe que esto consiste en círculos concéntricos centrados en el polo y líneas que pasan por el polo. Estos círculos y líneas tienen ecuaciones muy simples en coordenadas polares. Por ejemplo:

Considera la ecuación$r = 3$. Para que un punto esté en la gráfica de esta ecuación, debe estar en un círculo de radio 3 cuyo centro es el polo. Entonces la gráfica de esta ecuación es un círculo de radio 3 cuyo centro es el polo. También podemos mostrar esto convirtiendo la ecuación$r = 3$ a forma rectangular de la siguiente manera:

\[r = 3\]

\[r^{2} = 3^{2}\]

\[x^{2} + y^{2} = 9\]

En coordenadas rectangulares, esta es la ecuación de un círculo de radio 3 centrado en el origen.

Ahora considere la ecuación$\theta= \dfrac{\pi}{4}$. Para que un punto esté en la gráfica de esta ecuación, la línea a través del polo y este punto deben hacer un ángulo de$\dfrac{\pi}{4}$ radianes con el eje polar. Si solo permitimos valores positivos para$r$, la gráfica será un rayo con punto inicial en el polo que hace un ángulo de$\dfrac{\pi}{4}$ radianes con el eje polar. No obstante, si permitimos$r$ que sea cualquier número real, entonces obtenemos la línea a través del polo que hace un ángulo de$\dfrac{\pi}{4}$ radianes con el eje polar. Podemos convertir esta ecuación en coordenadas rectangulares de la siguiente manera:

\[\theta = \dfrac{\pi}{4}\]

\[\tan(\theta) = \tan(\dfrac{\pi}{4})\]

\[\dfrac{y}{x} = 1\]

\[y = x\]

Esta es una ecuación para una línea recta a través del origen con una pendiente de 1.

En general:

Definición

Si$a$ es un número real positivo, entonces la gráfica de$r = a$ es un círculo de radio$a$ cuyo centro es el polo.
Si$b$ es un número real, entonces la gráfica de$\theta = b$ es una línea a través del polo que hace un ángulo de$b$ radianes con el eje polar.

Observaciones Finales

Hemos estudiado solo algunas gráficas de ecuaciones polares. Hay muchas gráficas interesantes que se pueden generar usando ecuaciones polares que son muy difíciles de lograr en coordenadas rectangulares. Dado que el sistema de coordenadas polares se basa en círculos concéntricos, no debería sorprender que los círculos con centro en el polo tuvieran ecuaciones “simples” como$r = a$.

En Ejercicio$\PageIndex{5}$ y$\PageIndex{7}$, vimos ecuaciones polares cuyas gráficas eran círculos con centros no en el polo. Se trata de casos especiales de los siguientes:

Ecuaciones polares cuyas gráficas son círculos

Si$a$ es un número real positivo, entonces
La gráfica de$r = 2a\sin(\theta)$ es un círculo de radio$a$ con centro en el punto$(0, a)$ en coordenadas rectangulares o$(a, \dfrac{\pi}{2})$ en coordenadas polares.

La gráfica de$r = 2a\sin(\theta)$ es un círculo de radio$a$ con centro en el punto$(a, 0)$ en coordenadas rectangulares o$(a, 0)$ en coordenadas polares.

Exploraremos esta y las gráficas de otras ecuaciones polares en los ejercicios.

	Coordenadas polares	Coordenadas rectangulares
1.	\((3, \dfrac{\pi}{3})\)	\((\dfrac{3}{2}, \dfrac{3\sqrt{3}}{2})\)
2.	\((5, \dfrac{11\pi}{6})\)	\((\dfrac{5\sqrt{3}}{2}, -\dfrac{5}{2})\)
3.	\((-5, \dfrac{3\pi}{4})\)	\((\dfrac{5\sqrt{2}}{2}, -\dfrac{5\sqrt{2}}{2})\)

\(r = 4\sin(\theta)\)	\(\theta\)
\ (r = 4\ sin (\ theta)\) ">0	\ (\ theta\) ">0
\ (r = 4\ sin (\ theta)\) ">2	\ (\ theta\) ">\(\dfrac{\pi}{6}\)
\ (r = 4\ sin (\ theta)\) ">\(2\sqrt{2}\)	\ (\ theta\) ">\(\dfrac{\pi}{4}\)
\ (r = 4\ sin (\ theta)\) ">\(2\sqrt{3}\)	\ (\ theta\) ">\(\dfrac{\pi}{3}\)
\ (r = 4\ sin (\ theta)\) ">4	\ (\ theta\) ">\(\dfrac{\pi}{2}\)
\ (r = 4\ sin (\ theta)\) ">\(2\sqrt{3}\)	\ (\ theta\) ">\(\dfrac{2\pi}{3}\)
\ (r = 4\ sin (\ theta)\) ">\(2\sqrt{2}\)	\ (\ theta\) ">\(\dfrac{3\pi}{4}\)
\ (r = 4\ sin (\ theta)\) ">2	\ (\ theta\) ">\(\dfrac{5\pi}{6}\)
\ (r = 4\ sin (\ theta)\) ">0	\ (\ theta\) ">\(\pi\)

\(r = 4\sin(\theta)\)	\(\theta\)
\ (r = 4\ sin (\ theta)\) ">0	\ (\ theta\) ">\(\pi\)
\ (r = 4\ sin (\ theta)\) ">-2	\ (\ theta\) ">\(\dfrac{7\pi}{6}\)
\ (r = 4\ sin (\ theta)\) ">\(-2\sqrt{2}\)	\ (\ theta\) ">\(\dfrac{5\pi}{4}\)
\ (r = 4\ sin (\ theta)\) ">\(-2\sqrt{3}\)	\ (\ theta\) ">\(\dfrac{4\pi}{3}\)
\ (r = 4\ sin (\ theta)\) ">-4	\ (\ theta\) ">\(\dfrac{3\pi}{2}\)
\ (r = 4\ sin (\ theta)\) ">\(-2\sqrt{3}\)	\ (\ theta\) ">\(\dfrac{5\pi}{3}\)
\ (r = 4\ sin (\ theta)\) ">\(-2\sqrt{2}\)	\ (\ theta\) ">\(\dfrac{7\pi}{4}\)
\ (r = 4\ sin (\ theta)\) ">-2	\ (\ theta\) ">\(\dfrac{11\pi}{6}\)
\ (r = 4\ sin (\ theta)\) ">0	\ (\ theta\) ">\(\pi\)