2.3: Formulaciones de problemas

En esta sección, presentamos un problema simple, lo analizamos y aumentamos iterativamente su complejidad hasta que se parezca mucho al problema de alineación de secuencias. Esta sección debe ser vista como un calentamiento para la Sección 2.5 sobre el algoritmo Needleman-Wunsch.

Formulación 1: Subcadena común más larga

Como primer intento, supongamos que tratamos las secuencias de nucleótidos como cadenas sobre el alfabeto A, C, G y T. Dadas dos de estas cadenas, S1 y S2, podríamos intentar alinearlas encontrando la subcadena común más larga entre ellas. En particular, estas subcadenas no pueden tener brechas en ellas.

Como ejemplo, si S1 = ACGTCATCA y S2 = TAGTGTCA (consulte la Figura 2.4), la subcadena común más larga entre ellos es GTCA. Entonces en esta formulación, podríamos alinear S1 y S2 a lo largo de su subcadena común más larga, GTCA, para obtener la mayor cantidad de coincidencias. Un algoritmo simple sería intentar alinear S1 con diferentes desplazamientos de S2 y realizar un seguimiento de la coincidencia de subcadenas más larga encontrada hasta ahora. Tenga en cuenta que este algoritmo es cuadrático en la longitud de la secuencia más corta, que es más lenta de lo que preferiríamos para un problema tan simple.

Figura 2.4: Ejemplo de formulación de subcadena común más larga

Formulación 2: Subsecuencia común más larga (LCS)

Otra formulación es permitir brechas en nuestras subsecuencias y no limitarnos solo a subcadenas sin huecos. Dada una secuencia,\( \mathrm{X}=\left(x_{1}, \ldots, x_{m}\right) \) definimos formalmente\( Z=\left(z_{1}, \ldots, z_{k}\right) \) que es una subsecuencia de X si existe una secuencia estrictamente creciente\( i_{1}<i_{2}<\ldots<i_{k} \) de índices de X tal que para todos j,\( x_{i_{j}}=z_{j} \) (CLRS 350-1).

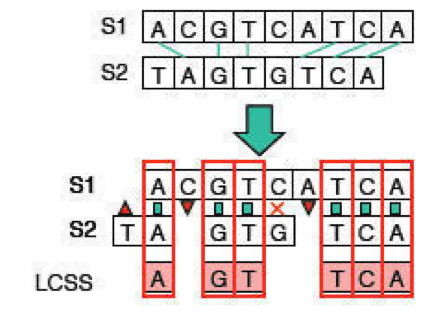
En el problema de la subsecuencia común más larga (LCS), se nos dan dos secuencias X e Y y queremos encontrar la subsecuencia común Z de longitud máxima. Consideremos el ejemplo de las secuencias S1 = ACGTCATCA y S2 = TAGTGTCA (consulte la Figura 2.5). La subsecuencia común más larga es AGTTCA, una coincidencia más larga que solo la subcadena común más larga.

Figura 2.5: Ejemplo de formulación de subsecuencia común más larga

Formulación 3: Alineación de Secuencias como Distancia de Edición

Formulación

La formulación anterior de LCS está cerca del problema de alineación de secuencias completas, pero hasta ahora no hemos especificado ninguna función de costo que pueda diferenciar entre los tres tipos de operaciones de edición (inserción, deleciones y sustituciones). Implícitamente, nuestra función de costo ha sido uniforme, lo que implica que todas las operaciones son igualmente probables. Dado que las sustituciones son mucho más probables, queremos sesgar nuestra solución LCS con una función de costo que prefiera las sustituciones sobre las inserciones y eliminaciones.

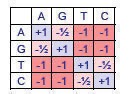
Refundimos la alineación de secuencias como un caso especial del problema clásico Edit-Distance ⁶ en informática (CLRS 366). Agregamos penalizaciones variables para diferentes operaciones de edición para reflejar ocurrencias biológicas. Un razonamiento biológico para esta decisión de puntuación es la probabilidad de que las bases se transcriban incorrectamente durante la polimerización. De las cuatro bases nucleotídicas, A y G son purinas (más grandes, dos anillos fusionados), mientras que C y T son pirimidinas (más pequeñas, un anillo). Así, la ADN polimerasa ⁷ es mucho más probable que confunda dos purinas o dos pirimidinas ya que son similares en estructura. La matriz de puntuación en la Figura 2.6 modela las consideraciones anteriores. Tenga en cuenta que la tabla es simétrica, esto es compatible con nuestro diseño reversible en el tiempo.

Figura 2.6: Matriz de costos para coincidencias y desajustes

El cálculo de las puntuaciones implica alternar entre la interpretación probabilística de la frecuencia con la que ocurren los eventos biológicos y la interpretación algorítmica de asignar una puntuación para cada operación. El problema es encontrar la secuencia de operación menos costosa (según la matriz de costos) que pueda transformar la secuencia inicial de nucleótidos en la secuencia de nucleótidos final.

Complejidad de la distancia de edición

Todos los algoritmos para resolver la distancia de edición entre dos cadenas operan en tiempo casi polinómico. En 2015, Backurs e Indyk [? ] publicó una prueba de que la distancia de edición no se puede resolver más rápido que\(O\left(n^{2}\right)\) en el caso general. Este resultado depende de la Hipótesis Fuerte del Tiempo Exponencial (SETH), que establece que los problemas NP-completos no pueden resolverse en tiempo subexponencial en el peor de los casos.

2.3.4 Formulación 4: Modelos de Costos Variables

Biológicamente, el costo de crear una brecha es más caro que el costo de extender una brecha ya creada. Así, podríamos crear un modelo que dé cuenta de esta variación de costos. Hay muchos modelos de este tipo que podríamos usar, incluyendo los siguientes:

• Penalización por hueco lineal: Costo fijo para todos los huecos (igual que la formulación 3).
• Penalización por brecha afín: Imponga un costo inicial grande para abrir una brecha, luego un costo incremental pequeño para cada extensión de brecha.

• Penalización por brecha general: Permitir cualquier función de costo. Tenga en cuenta que esto puede cambiar el tiempo de ejecución asintótico de nuestro algoritmo.

• Penalización por brecha consciente de fotogramas: Adapte la función de costo para tener en cuenta las interrupciones del marco de codificación (los indels que causan cambios de fotograma en los elementos funcionales generalmente causan modificaciones fenotípicas importantes).

2.3.5 Enumeración

Recordemos que para resolver la formulación de la Subcadena Común Más Larga, simplemente podríamos enumerar todas las alineaciones posibles, evaluar cada una y seleccionar la mejor. Esto se debió a que solo hubo alineaciones O (n) de las dos secuencias. Una vez que permitimos brechas en nuestra alineación, sin embargo, ya no es así. Es un problema conocido que no se puede enumerar el número de todas las alineaciones con huecos posibles (al menos cuando las secuencias son largas). Por ejemplo, con dos secuencias de longitud 1000, el número de posibles alineaciones supera el número de átomos en el universo.

Dada una métrica para puntuar una alineación dada, el algoritmo simple de fuerza bruta enumera todas las alineaciones posibles, calcula la puntuación de cada una y elige la alineación con la puntuación máxima. Esto lleva a la pregunta: '¿Cuántas alineaciones posibles hay?' Si considera solo NBA ⁸ n > m, el número de alineaciones es

\ [\ left (\ begin {array} {c}
n+m\\
m
\ end {array}\ right) =\ frac {(n+m)!} {n! m!} \ approx\ frac {(2 n)!} {(n!) ^ {2}}\ approx\ frac {\ sqrt {4\ pi n}\ frac {(2 n) ^ {2 n}} {e^ {2 n}}} {(\ sqrt {\ izquierda.2\ pi n\ frac {(n) ^ {n}} {e^ {n}}\ derecha) ^ {2}} =\ frac {2^ {2}} {\ sqrt {\ pi n}}\]

Este número crece extremadamente rápido, y para valores de n tan pequeños 30 es demasiado grande (> 10 ¹⁷) para que esta estrategia de enumeración sea factible. Por lo tanto, usar un algoritmo mejor que la fuerza bruta es una necesidad.

---

⁶ La distancia de edición o distancia Levenshtein es una métrica para medir la cantidad de diferencia entre dos secuencias (por ejemplo, la distancia Levenshtein aplicada a dos cadenas representa el número mínimo de ediciones necesarias para transformar una cadena en otra).

⁷ La ADN polimerasa es una enzima que ayuda a copiar una cadena de ADN durante la replicación.

⁸ Alineaciones no aburridas, o alineaciones donde los huecos siempre se emparejan con nucleótidos.