7.4: Aplicar HMM al Mundo Real- Del Casino a la Biología
- Page ID
- 54313
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El Casino Deshonesto
Imagina el siguiente escenario: Entras a un casino que ofrece un juego de dados rodando. Apostas $1 y luego tú y un repartidor tiran un dado. Si rotas un número más alto ganas $2. Ahora hay un giro en este juego aparentemente sencillo. Eres consciente de que el casino tiene dos tipos de dados:
- Muere justo: P (1) =P (2) =P (3) =P (4) =P (5) =P (6) =1/6
- Troquel cargado: P (1) = P (2) = P (3) = P (4) = P (5) = 1/10 y P (6) = 1/2
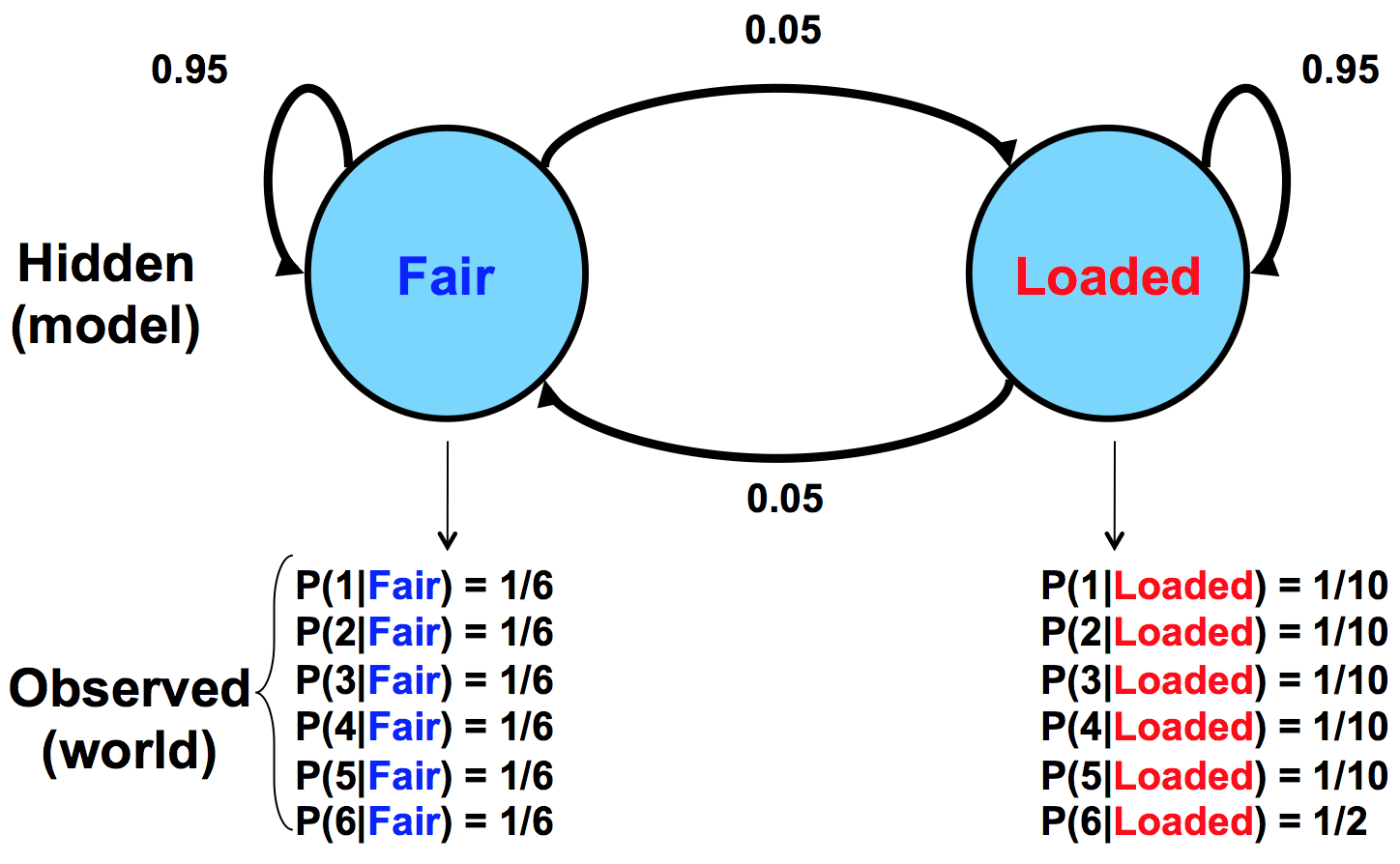
El crupier puede cambiar entre estos dos dados en cualquier momento sin que usted lo sepa. La única información que tienes son los rollos que observas. Podemos representar el estado del casino muere con un sencillo modelo de Markov:
El modelo muestra los dos estados posibles, sus emisiones y probabilidades de transición entre ellos. Las probabilidades de transición son conjeturas educadas en el mejor de los casos. Suponemos que el cambio entre los estados no ocurre con demasiada frecuencia, de ahí la probabilidad .95 de permanecer en el mismo estado con cada tirada.
Mantenerse en contacto con la biología: una analogía
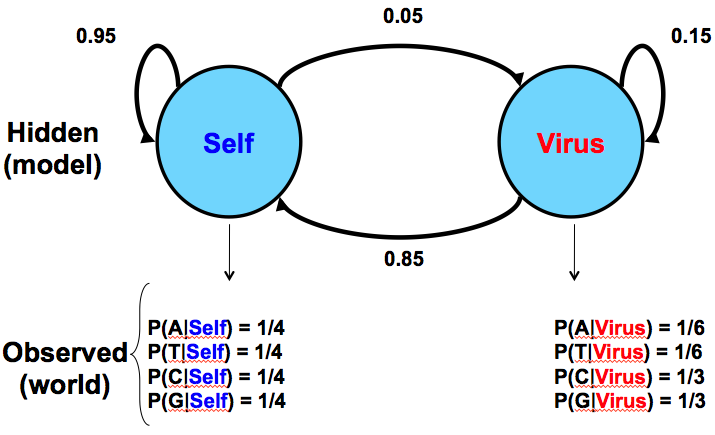
A modo de comparación, la Figura 7.5 a continuación da un modelo similar para una situación en biología donde una secuencia de ADN tiene dos fuentes potenciales: inyección por un virus versus producción normal por el propio organismo:
Dado este modelo como hipótesis, observaríamos las frecuencias de C y G para darnos pistas sobre la fuente de la secuencia en cuestión. Este modelo asume que los insertos virales tendrán mayor prevalencia de CpG, lo que conduce a las mayores probabilidades de ocurrencia de C y G.
Ejecución del modelo
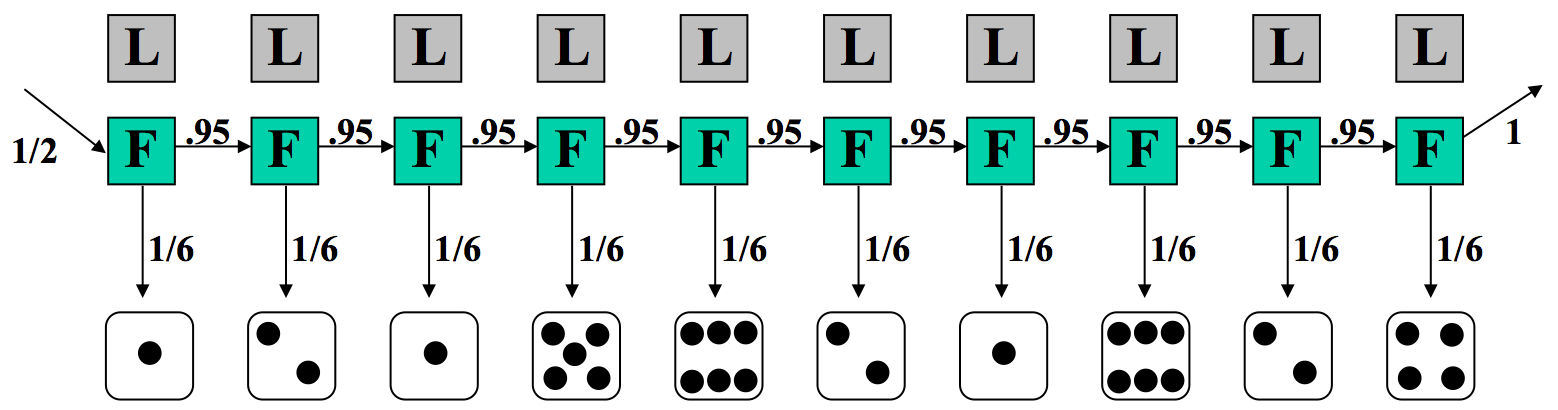
Digamos que estamos en el casino y observar la secuencia de rollos que se da en la Figura 7.6. Nos gustaría saber si es más probable que el casino esté usando el dado justo o el dado cargado.

Veamos una secuencia particular de rollos.
Por lo tanto, consideraremos dos posibles secuencias de estados en el HMM subyacente, una en la que el distribuidor siempre está usando un dado justo, y la otra en la que el distribuidor siempre está usando un dado cargado. Consideramos cada ruta de ejecución para entender las implicaciones. Para cada caso, calculamos la probabilidad conjunta de un resultado observado con esa secuencia de estados subyacentes.
En el primer caso, donde suponemos que el distribuidor siempre está utilizando un dado justo, las probabilidades de transición y emisión se muestran en la Figura 7.7. La probabilidad de esta secuencia de estados y emisiones observadas es producto de términos que pueden agruparse en tres componentes: 1/2, la probabilidad de comenzar con el dado justo; (1/6) 10, la probabilidad de la secuencia de rollos si siempre usamos el dado justo; y por último (0.95) 9, la probabilidad de que siempre sigamos usando el dado justo.
En este modelo, asumimos\(π = {F,F,F,F,F,F,F,F,F,F}\), y observamos\(x = {1,2,1,5,6,2,1,6,2,4}\).
Ahora podemos calcular la probabilidad conjunta de x y π de la siguiente manera:
\ [\ begin {alineado}
P (x,\ pi) &=P (x\ mid\ pi) P (\ pi)\\
&=\ frac {1} {2}\ veces P (1\ mid F)\ times P (F\ mid F)\ times P (2\ mid F)\ cdots\\
&=\ frac {1} {2}\ times\ left (\ frac {1} {6}\ derecha) ^ {10}\ veces (0.95) ^ {9}\\
&=5.2\ veces 10^ {-9}
\ end {alineado}\ nonumber\]
Con una probabilidad tan pequeña, este podría parecer un caso extremadamente improbable. En la actualidad, la probabilidad es baja porque hay muchas posibilidades igualmente probables, y ningún resultado es probable a priori. La cuestión no es si esta secuencia de estados ocultos es probable, sino si es más probable que las alternativas.
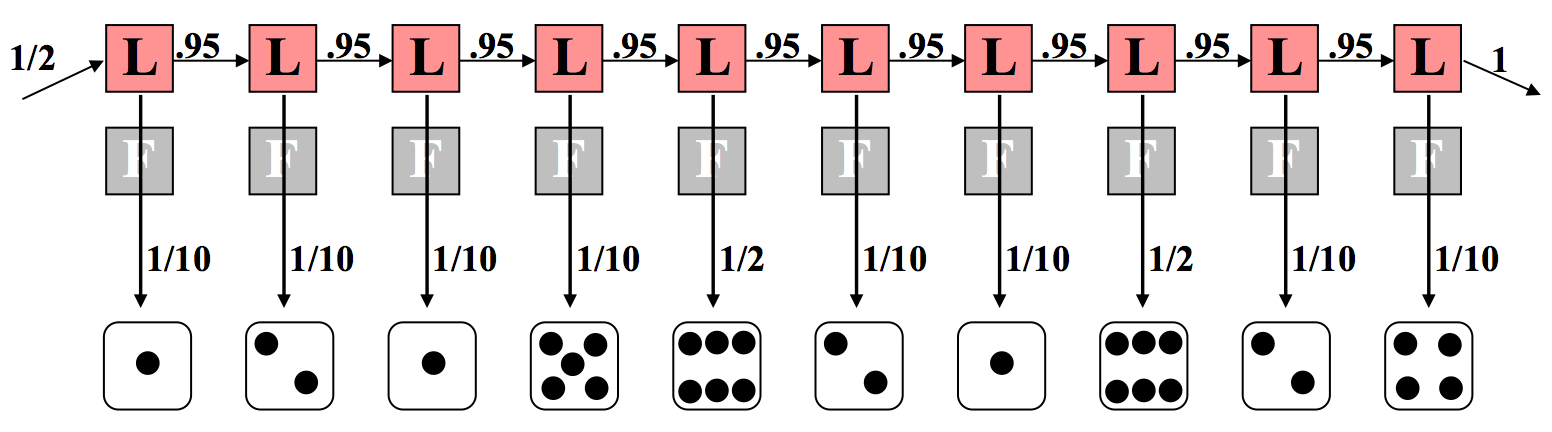
Consideremos el extremo opuesto donde el distribuidor siempre usa un dado cargado, como se muestra en la Figura 7.8. Esto tiene un cálculo similar excepto que observamos una diferencia en el componente de emisión. Esta vez, 8 de los 10 rollos llevan una probabilidad de 1/10 porque el dado cargado desfavorece a los no seis. Los dos rollos restantes de seis tienen cada uno una probabilidad de 1/2 de ocurrir. Nuevamente multiplicamos todas estas probabilidades juntas según principios de independencia y condicionamiento. En este caso, los cálculos son los siguientes:
\ [\ start {align*}
P (x,\ pi) &=\ frac {1} {2}\ veces P (1\ mid L)\ times P (L\ mid L)\ times P (2\ mid L)\ cdots\\
&=\ frac {1} {2}\ times\ left (\ frac {1} {10}\ right) ^ {8}\ veces izquierda\ (\ frac {1} {2}\ derecha) ^ {2}\ veces (0.95) ^ {9}\\
&=7.9\ veces 10^ {-10}
\ end { alinear*}\]
Anote la diferencia en los exponentes. Si hacemos una comparación directa, podemos decir que la situación en la que se usa un dado justo a lo largo de la secuencia es de 52 × 10 −10 (en comparación con 7.9 × 10 −10 con el dado cargado).
Por lo tanto, es seis veces más probable que se utilizó el dado justo que el dado cargado. Esto no es demasiado sorprendente—dos rollos de cada diez que arrojan un 6 no está muy lejos del esperado número 1.7 con el dado justo, y más lejos del esperado número 5 con el dado cargado.
Agregando complejidad
Ahora imagina el caso más complejo, e interesante, donde el distribuidor cambia el dado en algún momento durante la secuencia. Hacemos una conjetura a un modelo subyacente basado en esta premisa en la Figura 7.9.
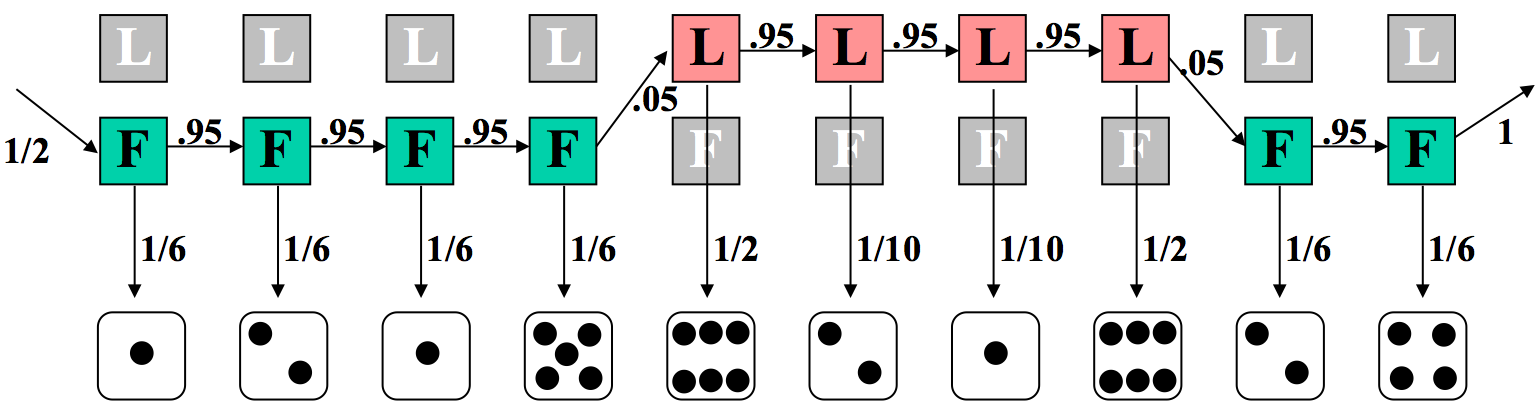
Nuevamente, podemos calcular la probabilidad de la probabilidad conjunta de esta secuencia de estados y observaciones. Aquí, seis de los rollos se calculan con el troquel justo, y cuatro con el cargado. Además, ya no todas las probabilidades de transición son del 95%. Los dos swaps (entre justos y cargados) tienen cada uno una probabilidad del 5%.
\ [\ start {alineado}
P (x,\ pi) &=\ frac {1} {2}\ veces P (1\ mid L)\ times P (L\ mid L)\ times P (2\ mid L)\ cdots\\
&=\ frac {1} {2}\ times\ left (\ frac {1} {10}\ right) ^ {2}\ times\ left (\ frac {1} {2}\ derecha) ^ {2}\ veces\ izquierda (\ frac {1} {6}\ derecha) ^ {6}\ veces (0.95) ^ {7}\ veces (0.05) ^ {2}\\
&=4.67\ times 10^ {-11}
\ end {alineado}\ nonumber\]
Volver a Biología
Ahora que hemos formalizado los HMM, queremos utilizarlos para resolver algunos problemas biológicos reales. De hecho, los HMM son una gran herramienta para el análisis de secuencias génicas, porque podemos ver una secuencia de ADN como emitida por una mezcla de modelos. Estos pueden incluir intrones, exones, factores de transcripción, etc. Si bien podemos tener algunos datos de muestra que emparejan modelos con secuencias de ADN, en el caso de que empecemos de nuevo con una nueva pieza de ADN, podemos usar HMM para atribuir algunos modelos potenciales al ADN en cuestión. Primero presentaremos un ejemplo sencillo y lo pensaremos un poco. Luego, discutiremos algunas aplicaciones de HMM en la resolución de preguntas biológicas interesantes, antes de finalmente describir las técnicas HMM que resuelven los problemas que surgen en tal análisis de primer trato/nativo.
Un ejemplo sencillo: Encontrar regiones ricas en GC
Imagínese el siguiente escenario: estamos tratando de encontrar regiones ricas en GC modelando secuencias de nucleótidos extraídas de dos distribuciones diferentes: fondo y promotor. Las regiones de fondo tienen una distribución uniforme de 0.25 para cada una de A, T, G, C. Las regiones promotoras tienen probabilidades: A: 0.15, T: 0.13, G: 0.30, C: 0.42. Dado un nucleótido observado, no podemos decir nada sobre la región de la que se originó, ya que cualquiera de las regiones emitirá cada nucleótido con cierta probabilidad. Podemos aprender estas probabilidades de estado inicial con base en probabilidades de estado estacionario. Al observar una secuencia, queremos identificar qué regiones se originan a partir de una distribución de fondo (B) y qué regiones son de un modelo promotor (P).
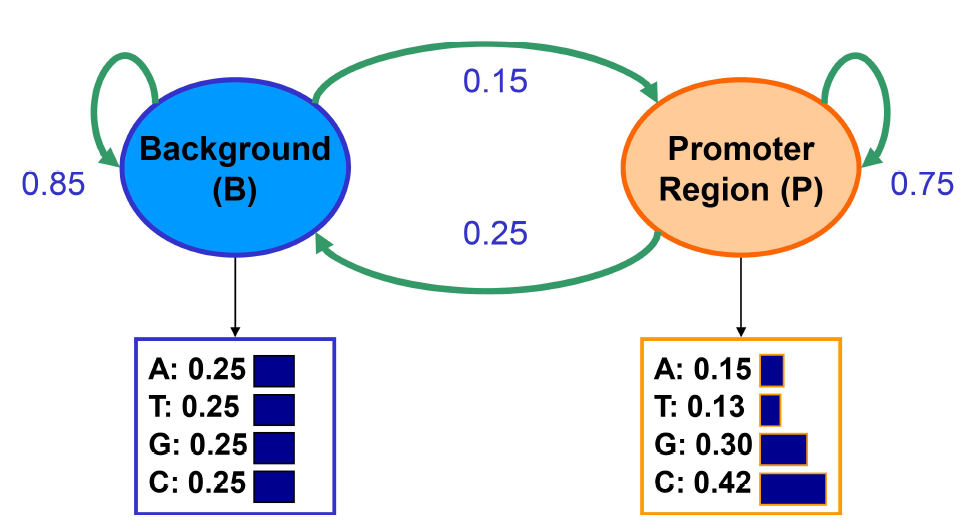
Se nos dan las probabilidades de transición y emisión basadas en abundancia relevante y longitud promedio de regiones donde x = vector de emisiones observables que consiste en símbolos del alfabeto {A, T, G, C}; π = vector de estados en una ruta (e.g. BPPBP); π ∗ = probabilidad máxima de generar ese camino. En nuestra interpretación de secuencia, la ruta de máxima verosimilitud se encontrará incorporando todas las probabilidades de emisión y transición por programación dinámica.
Los HMM son modelos generativos, en que un HMM da la probabilidad de emisión dado un estado (usando la Regla de Bayes), esencialmente diciéndote cuán probable es que el estado genere esas secuencias. Así que siempre podemos ejecutar un modelo generativo para las transiciones entre estados y comenzar en cualquier lugar. En Cadenas de Markov, el próximo estado dará diferentes resultados con diferentes probabilidades. No importa qué estado sea el siguiente, en el siguiente estado, el siguiente símbolo seguirá saliendo con diferentes probabilidades. Los HMM son similares: Se puede elegir un estado inicial basado en el vector de probabilidad inicial. En el ejemplo anterior, comenzaremos en el estado B con alta probabilidad ya que la mayoría de las localizaciones no corresponden a regiones promotoras. Luego se dibuja una emisión de la P (X|B). Cada nucleótido ocurre con probabilidad 0.25 en el estado de fondo. Digamos que el nucleótido muestreado es una G. La distribución de los estados subsiguientes depende únicamente del hecho de que estamos en estado de fondo y es independiente de esta emisión. Entonces tenemos que la probabilidad de permanecer en el estado B es de 0.85 y la probabilidad de transición al estado P es de 0.15, y así sucesivamente.
Podemos calcular la probabilidad de una de esas generaciones multiplicando las probabilidades de que el modelo haga exactamente las elecciones que asumimos. Considere los ejemplos mostrados en las Figuras 7.11, 7.12 y 7.13.
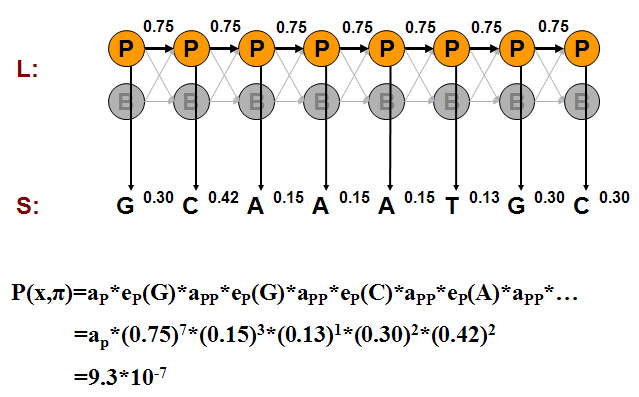
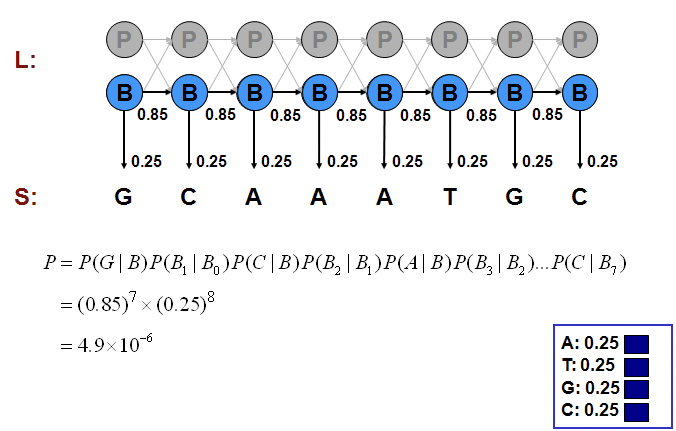
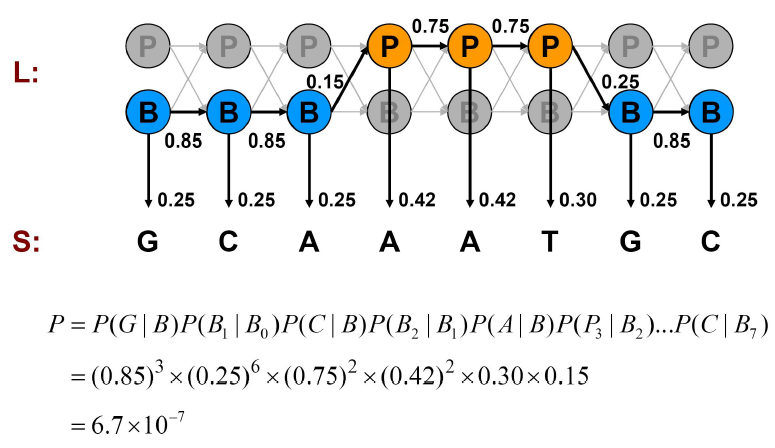
Podemos calcular la probabilidad conjunta de una secuencia particular de estados correspondientes a las emisiones observadas como hicimos en los ejemplos del Casino:
\ [\ comenzar {alineado}
P\ izquierda (x,\ pi_ {P}\ derecha) &=a_ {P}\ veces e_ {P} (G)\ veces a_ {P}\ veces e_ {P} (G)\ veces\ cdots\\
&=a_ {P}\ veces (0.75) ^ {7}\ veces (0.15) ^ {3}\ veces (0.13)\ veces (0.3) ^ {2}\ veces (0.42) ^ {2}\\
&=9.3\ veces 10^ {-7}\\
P\ izquierda (x,\ pi_ {B}\ derecha) &= (0.85) ^ {7}\ veces (0.25) ^ {8}\\
&=4.9\ veces 10^ {-6}\
P\ izquierda (x,\ pi_ {\ texto {mixto}}\ derecha) & =( 0.85) ^ {3}\ veces (0.25) ^ {6}\ veces (0.75) ^ {2}\ veces (0.42) ^ {2}\ times 0.3\ times 0.15\\
&=6.7\ times 10^ {-7}
\ end {alineado}\ nonumber\]
La alternativa de fondo puro es la opción más probable de las posibilidades que hemos examinado. Pero, ¿cómo sabemos si es la opción más probable de todos los caminos posibles de los estados haber generado la secuencia observada?
El enfoque de fuerza bruta consiste en examinar en todos los caminos, probando todas las posibilidades y calculando sus probabilidades conjuntas P (x, π) como hicimos anteriormente. La suma de probabilidades de todas las alternativas es 1. Por ejemplo, si todos los estados son promotores,\( P(x, \pi)=9.3 \times 10^{-7} \). Si todas las emisiones son Gs,\(P(x, \pi)=4.9 \times 10^{-6}\). la mezcla de B's y P's como en la Figura 7.13, P (x, π) = 6.7 × 10 −7; que es pequeña porque se paga mucha penalización por las transiciones entre B's y P's que son exponenciales en longitud de secuencia. Por lo general, si observas más G, es más probable que esté en la región promotora y si observas más A y Ts, entonces es más probable que esté en segundo plano. Pero necesitamos algo más que solo observación para apoyar nuestra creencia. Veremos cómo podemos apoyar matemáticamente nuestra intuición en las siguientes secciones.
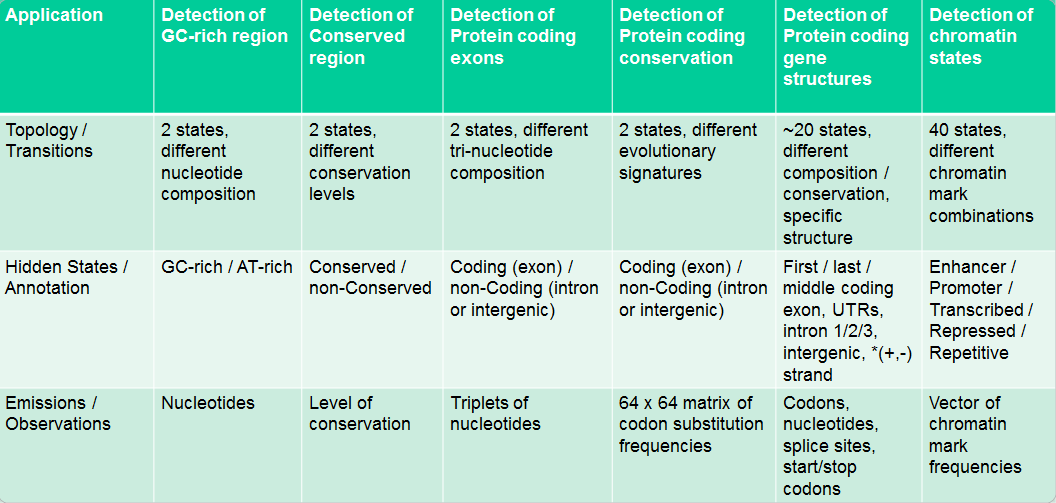
Aplicación de HMM en Biología
Los HMM se utilizan para responder muchas preguntas biológicas interesantes. Algunas aplicaciones biológicas de los HMM se resumen en la Figura 7.14.