20.3: Revisión de álgebra lineal

Nuestro objetivo de esta sección es recordarte algunos conceptos que aprendiste en tu clase de álgebra lineal. Esto no pretende ser un recorrido detallado. Si quieres aprender más sobre alguno de los siguientes conceptos, te recomiendo recoger un libro de álgebra lineal y leer de esa sección. Pero esto servirá como un buen recordatorio y señalar conceptos que son importantes para nosotros en este capítulo.

vectores propios

Dada una matriz cuadrada A,\((m \times m)\), el autovector v es la solución a la siguiente ecuación.

\[A v=\lambda v \nonumber \]

En otras palabras, si multiplicamos la matriz por ese vector, solo cambiamos nuestra posición paralela al vector (recuperamos una versión escalada del vector v).

Y\(\lambda\) (cuánto se escala el vector v) se llama el valor propio.
Entonces, ¿cuántos valores propios hay como máximo? Demos los primeros pasos para resolver esta ecuación.

\[A v=\lambda v \Rightarrow(A-\lambda I) v=0 \nonumber \]
que tiene soluciones distintas de cero cuando\(|A-\lambda I|=0\). Esa es una ecuación de orden m-ésimo en la\(\lambda\) que puede tener como máximo m soluciones distintas. Recuerda que esas soluciones pueden ser complejas, aunque A sea real.

Descomposición vectorial

Dado que los vectores propios forman el conjunto de todas las bases, representan completamente el espacio de columna. Dado eso, podemos descomponer cualquier vector arbitrario x en una combinación de vectores propios.

\[x=\sum_{i} c_{i} v_{i} \nonumber \]

Así, cuando multiplicamos un vector con una matriz A, podemos reescribirlo en términos de los vectores propios.

\ [\ begin {array} {c}
A x=A\ izquierda (c_ {1} v_ {1} +c_ {2} v_ {2} +\ ldots\ derecha)\\
A x=c_ {1} A v_ {1} +c_ {2} A_ {v} 2+\ ldots\\
A x=c_ {1}\ lambda_ {1} _ {1} +c_ {2}\ lambda_ {2} v_ {2} +c_ {3}\ lambda_ {3} v_ {3} +\ ldots
\ end {array}\ nonumber\]
Entonces la acción de A on x está determinado por los valores propios de y los vectores propios. Y podemos observar que los valores propios pequeños tienen un pequeño eect en la multiplicación.

¿Sabías?

• Para matrices simétricas, los vectores propios para valores propios distintos son ortogonales.

• Todos los valores propios de una matriz simétrica real son reales.
• Todos los valores propios de una matriz semidefinita positiva no son negativos.

Descomposición Diagonal

También conocido como Eigen Descomposición. Sea S una\(m \times m \) matriz cuadrada con m vectores propios linealmente independientes (una matriz no defectuosa).

Luego, existe una descomposición (teorema de digitalización matricial)\[ S=U \Lambda U^{-1} \nonumber \]

Donde las columnas de U son los vectores propios de S. Y\(\Lambda\) es una matriz diagonal con valores propios en su diagonal.

Descomposición del Valor Singular

A menudo, la descomposición de valores singulares (SVD) se utiliza para el caso más general de factorizar una matriz\(m \times n\) no cuadrada:

\[\mathbf{A}=\mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^{T}\]

donde U es una\(m \times m \) matriz que representa vectores propios ortogonales de AA ^_T, V es una\(n \times n \) matriz que representa vectores propios ortogonales de A ^T A y V es una\(n \times n\) matriz que representa raíces cuadradas de los valores propios de A ^T A (llamados valores singulares de A):

\[ \mathbf{\Sigma}=\operatorname{diag}\left(\sigma_{1}, \ldots, \sigma_{r}\right), \sigma_{i}=\sqrt{\lambda_{i}} \]

El SVD de cualquier matriz dada se puede calcular con un solo comando en Matlab y no cubriremos los detalles técnicos de computarlo. Tenga en cuenta que la matriz “diagonal” resultante\(\mathbf{\Sigma} \) puede no ser de rango completo, es decir, puede tener diagonales cero, y el número máximo de valores singulares distintos de cero es min (m, n).

Por ejemplo, vamos

\ [A=\ left [\ begin {array} {cc}
1 & -1\\
1 & 0\\
1 & 0
\ end {array}\ derecha]\ nonumber\]

así m=3, n=2. Su SVD es

\ [\ left [\ begin {array} {ccc}
0 &\ frac {2} {\ sqrt {6}} &\ frac {1} {\ sqrt {3}}\
\ frac {1} {\ sqrt {2}} & -\ frac {1} {\ sqrt {6}} &\ frac {1} {\ sqrt {3}}\
\ frac {1} {\ sqrt {2}} &\ frac {1} {\ sqrt {6}} & -\ frac {1} {\ sqrt {3}}
\ end {array}\ derecha]\ izquierda [\ begin {array} {cc}
1 & 0\\
0 &\ sqrt {3}\\
0 & 0
\ end {array}\ derecha]\ izquierda [\ begin {array} {cc}
\ frac {1} {\ sqrt {2}} &\ frac {1} {\ sqrt {2}}\
\ frac {1} {\ sqrt {2}} & -\ frac {1} {\ sqrt {2}}
\ end {array}\ derecha]\ nonumber\]

Típicamente, los valores singulares están dispuestos en orden decreciente.

La SVD es ampliamente utilizada en técnicas estadísticas, de análisis numérico y de procesamiento de imágenes. Una aplicación típica de SVD es la aproximación óptima de rango bajo de una matriz. Por ejemplo, si tenemos una gran matriz de datos, por ejemplo 1000 por 500, y nos gustaría aproximarla con una matriz de rango inferior sin mucha pérdida de información, formulada como el siguiente problema de optimización:

Encuentra A _k de rango k tal que\(\mathbf{A}_{k}=\min _{\mathbf{X}: r a n k(\mathbf{X})=k}\|\mathbf{A}-\mathbf{X}\|_{F} \)

donde el subíndice F denota la norma Frobenius\(\|\mathbf{A}\|_{F}=\sqrt{\sum_{i} \sum_{j}\left|a_{i j}\right|^{2}}\). Por lo general, k es mucho menor que r. La solución a este problema es la SVD de X\(\mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^{T}\), con los valores singulares de r-k más pequeños en\(\mathbf{\Sigma}\) conjunto a cero:

\[\mathbf{A}_{k}=\operatorname{Udiag}\left(\sigma_{1}, \ldots, \sigma_{k}, \ldots, 0\right) \mathbf{V}^{T} \nonumber \]

Tal aproximación se puede demostrar que tiene un error de\(\left\|\mathbf{A}-\mathbf{A}_{k}\right\|_{F}=\sigma_{k+1}\). Esto también se conoce como el teorema de Eckart-Young.

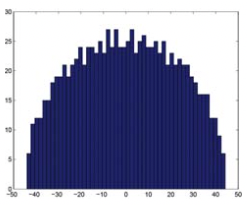
Una aplicación común de SVD al análisis de red es usar la distribución de valores singulares de la matriz de adyacencia para evaluar si nuestra red parece una matriz aleatoria. Debido a que la distribución de los valores singulares (ley de semicírculo Wigner) y la del valor propio más grande de una matriz (distribución Tracy-Widom) se han derivado teóricamente, es posible derivar la distribución de valores propios (valores singulares en SVD) de una red observada (matriz), y calcular un p- valor para cada uno de los valores propios. Entonces solo necesitamos mirar los valores propios significativos (valores singulares) y sus correspondientes vectores propios (vectores singulares) para examinar estructuras significativas en la red. La siguiente figura muestra la distribución de valores singulares de un conjunto unitario gaussiano aleatorio (GUE, ver este enlace de Wikipedia para definición y propiedades en.wikipedia.org/wiki/Random_matrix) matriz, que forman un semicírculo de acuerdo con la ley de semicírculo de Wigner (Figura 20.4).

Un ejemplo del uso de SVD para inferir patrones estructurales en una matriz o red se muestra en la Figura 20.5. El panel superior izquierdo muestra una estructura (roja) añadida a una matriz aleatoria (fondo azul en el mapa de calor), que abarca la primera fila y las tres primeras columnas. SVD detecta esto mediante la identificación de un gran valor singular (circular en rojo en la distribución de valores singulares) y cargas de fila grandes correspondientes (U1) así como tres cargas de columnas grandes (V1). A medida que se agregan más estructuras a la red (paneles superior derecha e inferior), se pueden descubrir usando SVD observando los siguientes valores singulares más grandes y las cargas de fila/columna correspondientes, etc.

Figura 20.4: Ley de semicírculo Wigner