2.3: Máxima verosimilitud
- Page ID
- 53855
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Sección 2.3a: ¿Qué es una probabilidad?
Dado que todos los enfoques descritos en el resto de este capítulo implican calcular las probabilidades, primero describiré brevemente este concepto. Una buena revisión general de verosimilitud es Edwards (1992). La verosimilitud se define como la probabilidad, dado un modelo y un conjunto de valores de parámetros, de obtener un conjunto particular de datos. Es decir, dada una descripción matemática del mundo, ¿cuál es la probabilidad de que veamos los datos reales que hemos recopilado?
Para calcular una verosimilitud, tenemos que considerar un modelo particular que pudo haber generado los datos. Ese modelo casi siempre tendrá valores de parámetros que deben especificarse. Podemos referirnos a este modelo especificado (con valores de parámetros particulares) como hipótesis, H. La probabilidad es entonces:
\[L(H|D)=Pr(D|H) \label{2.1}\]
Aquí, L y Pr representan verosimilitud y probabilidad, D para los datos y H para la hipótesis, que nuevamente incluye tanto el modelo que se está considerando como un conjunto de valores de parámetros. El símbolo | significa “dado”, por lo que la ecuación 2.1 puede leerse como “la probabilidad de la hipótesis dada los datos es igual a la probabilidad de los datos dada la hipótesis”. En otras palabras, la verosimilitud representa la probabilidad bajo un modelo dado y valores de parámetros de que obtendríamos los datos que realmente vemos.
Para cualquier modelo dado, el uso de diferentes valores de parámetros generalmente cambiará la probabilidad. Como se puede adivinar, favorecemos los valores de parámetros que nos dan la mayor probabilidad de obtener los datos que vemos. Una forma de estimar los parámetros a partir de los datos, entonces, es encontrando los valores de los parámetros que maximicen la probabilidad; es decir, los valores de los parámetros que dan la mayor probabilidad, y la mayor probabilidad de obtener los datos. Estas estimaciones se denominan entonces estimaciones de máxima verosimilitud (ML). En un marco de ML, suponemos que la hipótesis que mejor se ajuste a los datos es la que tiene la mayor probabilidad de haber generado esos datos.
Para el ejemplo anterior, necesitamos calcular la probabilidad como la probabilidad de obtener cabezas 63 de cada 100 volteretas de lagarto, dado algún modelo de volteo de lagarto. En general, podemos escribir la probabilidad de cualquier combinación de H “éxitos” (volteretas que dan cabezas) de n ensayos. También tendremos un parámetro, p H, que representará la probabilidad de “éxito”, es decir, la probabilidad de que cualquier volteo aparezca de cabeza. Podemos calcular la probabilidad de nuestros datos usando el teorema binomial:
\[ L(H|D)=Pr(D|p)= {n \choose H} p_H^H (1-p_H)^{n-H} \label{2.2} \]
En el ejemplo dado, n = 100 y H = 63, así:
\[ L(H|D)= {100 \choose 63} p_H^{63} (1-p_H)^{37} \label{2.3} \]
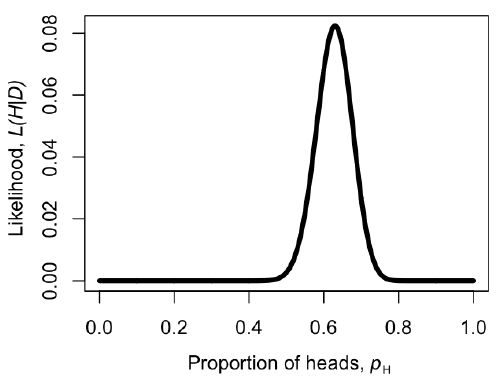
Podemos hacer una gráfica de la verosimilitud, L, en función de p H (Figura 2.2). Cuando hacemos esto, vemos que el valor de máxima verosimilitud de p H, al que podemos llamar $\ hat {p} _H$, está en $\ hat {p} _H = 0.63$. Este es el enfoque de “fuerza bruta” para encontrar la máxima verosimilitud: pruebe muchos valores diferentes de los parámetros y elija el que tenga la mayor probabilidad. Podemos hacer esto de manera mucho más eficiente usando métodos numéricos como se describe en capítulos posteriores de este libro.
También podríamos haber obtenido la estimación de máxima verosimilitud para p H a través de la diferenciación. Este problema es mucho más fácil si trabajamos con la probabilidad de lin en lugar de con la probabilidad misma (tenga en cuenta que cualquier valor de p H que maximice la probabilidad también maximizará la probabilidad de lin, porque la función log está aumentando estrictamente). Entonces:
\[ \ln{L} = \ln{n \choose H} + H \ln{p_H}+ (n-H)\ln{(1-p_H)} \label{2.4} \]
Tenga en cuenta que la transformación logarítmica natural (ln) cambia nuestra ecuación de una función de potencia a una función lineal que es fácil de resolver. Podemos diferenciar:
\[ \frac{d \ln{L}}{dp_H} = \frac{H}{p_H} - \frac{(n-H)}{(1-p_H)}\label{2.5} \]
El máximo de la verosimilitud representa un pico, que podemos encontrar estableciendo la derivada $\ frac {d\ ln {L}} {dp_h} $ a cero. Luego encontramos el valor de p H que resuelve esa ecuación, que será nuestra estimación $\ hat {p} _H$. Así que tenemos:
\[ \begin{array}{lcl} \frac{H}{\hat{p}_H} - \frac{n-H}{1-\hat{p}_H} & = & 0\\ \frac{H}{\hat{p}_H} & = & \frac{n-H}{1-\hat{p}_H}\\ H (1-\hat{p}_H) & = & \hat{p}_H (n-H)\\ H-H\hat{p}_H & = & n\hat{p}_H-H\hat{p}_H\\ H & = & n\hat{p}_H\\ \hat{p}_H &=& H / n\\ \end{array} \label{2.6}\]
Observe que, para nuestro ejemplo sencillo, H/n = 63/100 = 0.63, que es exactamente igual a la máxima verosimilitud de la figura 2.2.
Las estimaciones de máxima verosimilitud tienen muchas propiedades estadísticas deseables. Vale la pena señalar, sin embargo, que no siempre devolverán estimaciones precisas de parámetros, incluso cuando los datos se generen bajo el modelo real que estamos considerando. De hecho, los parámetros ML a veces pueden estar sesgados. Para entender lo que esto significa, necesitamos introducir formalmente dos nuevos conceptos: sesgo y precisión. Imagínese que íbamos a simular conjuntos de datos bajo algún modelo A con el parámetro a. para cada simulación, luego usamos ML para estimar el parámetro $\ hat {a} $ para los datos simulados. La precisión de nuestra estimación de ML nos dice cuán diferentes son, en promedio, cada uno de nuestros parámetros estimados $\ hat {a} _i$ entre sí. Las estimaciones precisas se estiman con menos incertidumbre. El sesgo, por otro lado, mide qué tan cerca están nuestras estimaciones $\ hat {a} _i$ del verdadero valor a. Si nuestra estimación del parámetro ML está sesgada, entonces el promedio de $\ hat {a} _i$ diferirá del valor verdadero a. No es raro que las estimaciones de ML estén sesgadas de una manera que depende del tamaño de la muestra, de manera que las estimaciones se acercan a la verdad a medida que aumenta el tamaño de la muestra, pero pueden estar bastante alejadas en una dirección particular cuando el número de puntos de datos es pequeño en comparación con el número de parámetros que se estiman.
En nuestro ejemplo de volteo de lagarto, estimamos un valor de parámetro de $\ hat {p} _H = 0.63$. Para el caso particular de estimar el parámetro de una distribución binomial, se sabe que nuestra estimación ML es imparcial. Y esta estimación es diferente de 0.5 —que era nuestra expectativa bajo la hipótesis nula. Entonces, ¿esta lagartija es justa? O, alternativamente, ¿podemos rechazar la hipótesis nula de que p H = 0.5? Para evaluar esto, necesitamos usar la selección de modelos.
Sección 2.3b: La prueba de razón de verosimilitud
La selección de modelos implica comparar un conjunto de modelos potenciales y usar algún criterio para seleccionar el que proporcione la “mejor” explicación de los datos. Diferentes enfoques definen “mejor” de diferentes maneras. Primero discutiré la más simple, pero también la más limitada, de estas técnicas, la prueba de cociente de verosimilitud. Las pruebas de relación de verosimilitud solo pueden utilizarse en una situación particular: para comparar dos modelos donde uno de los modelos es un caso especial del otro. Esto significa que el modelo A es exactamente equivalente al modelo B más complejo con parámetros restringidos a ciertos valores. Siempre podemos identificar el modelo más simple como el modelo con menos parámetros. Por ejemplo, quizás el modelo B tiene parámetros x, y y z que pueden tomar cualquier valor. El modelo A es el mismo que el modelo B pero con el parámetro z fijado en 0. Es decir, A es el caso especial de B cuando el parámetro z = 0. Esto a veces se describe como el modelo A está anidado dentro del modelo B, ya que cada versión posible del modelo A es igual a un caso determinado del modelo B, pero el modelo B también incluye más posibilidades.
Para las pruebas de razón de verosimilitud, la hipótesis nula es siempre la más simple de los dos modelos. Comparamos los datos con lo que esperaríamos si el modelo más simple (nulo) fuera correcto.
Por ejemplo, consideremos de nuevo nuestro ejemplo de voltear un lagarto. Un modelo es que el lagarto es “justo”: es decir, que la probabilidad de cabezas es igual a 1/2. Un modelo diferente podría ser que la probabilidad de cabezas sea algún otro valor p, que podría ser 1/2, 1/3, o cualquier otro valor entre 0 y 1. Aquí, el último modelo (complejo) tiene un parámetro adicional, p H, comparado con el modelo anterior (simple); el modelo simple es un caso especial del modelo complejo cuando p H = 1/2.
Para tales modelos anidados, se puede calcular el estadístico de prueba de relación de verosimilitud como
\[ \Delta = 2 \cdot \ln{\frac{L_1}{L_2}} = 2 \cdot (\ln{L_1}-\ln{L_2}) \label{2.7}\]
Aquí, Δ es el estadístico de prueba de razón de verosimilitud, L 2 la probabilidad del modelo más complejo (rico en parámetros) y L 1 la probabilidad del modelo más simple. Dado que los modelos están anidados, la probabilidad del modelo complejo siempre será mayor o igual que la probabilidad del modelo simple. Esto es consecuencia directa del hecho de que los modelos están anidados. Si encontramos una probabilidad particular para el modelo más simple, siempre podemos encontrar una probabilidad igual a la del modelo complejo estableciendo los parámetros para que el modelo complejo sea equivalente al modelo simple. Entonces, la probabilidad máxima para el modelo complejo será ese valor, o algún valor superior que podamos encontrar a través de la búsqueda del espacio de parámetros. Esto significa que el estadístico de prueba Δ nunca será negativo. De hecho, si alguna vez obtiene una estadística de prueba de razón de verosimilitud negativa, algo ha salido mal, o sus cálculos están equivocados, o no ha encontrado soluciones ML, o los modelos no están realmente anidados.
Para realizar una prueba estadística comparando los dos modelos, comparamos el estadístico de prueba Δ con su expectativa bajo la hipótesis nula. Cuando los tamaños de muestra son grandes, la distribución nula del estadístico de prueba de razón de verosimilitud sigue una distribución chi-cuadrado (χ 2) con grados de libertad iguales a la diferencia en el número de parámetros entre los dos modelos. Esto significa que si la hipótesis más simple fuera cierta, y se realizara esta prueba muchas veces en grandes conjuntos de datos independientes, el estadístico de prueba seguiría aproximadamente esta distribución de χ 2. Para rechazar el modelo más simple (nulo), entonces, se compara el estadístico de prueba con un valor crítico derivado de la distribución de χ 2 apropiada. Si el estadístico de prueba es mayor que el valor crítico, se rechaza la hipótesis nula. De lo contrario, no rechazamos la hipótesis nula. En este caso, solo necesitamos considerar una cola de la prueba de χ 2, ya que cada desviación del modelo nulo nos empujará hacia valores δ más altos y hacia la cola derecha de la distribución.
Para el ejemplo de volteo de lagarto anterior, podemos calcular la probabilidad ln bajo una hipótesis de p H = 0.5 como:
\[ \begin{array}{lcl} \ln{L_1} &=& \ln{\left(\frac{100}{63}\right)} + 63 \cdot \ln{0.5} + (100-63) \cdot \ln{(1-0.5)} \nonumber \\ \ln{L_1} &=& -5.92\nonumber\\ \end{array} \label{2.8}\]
Podemos comparar esto con la probabilidad de nuestra estimación de máxima verosimilitud:
\[ \begin{array}{lcl} \ln{L_2} &=& \ln{\left(\frac{100}{63}\right)} + 63 \cdot \ln{0.63} + (100-63) \cdot \ln{(1-0.63)} \nonumber \\ \ln{L_2} &=& -2.50\nonumber \end{array} \label{2.9}\]
Luego calculamos el estadístico de prueba de relación de verosimilitud:
\[ \begin{array}{lcl} \Delta &=& 2 \cdot (\ln{L_2}-\ln{L_1}) \nonumber \\ \Delta &=& 2 \cdot (-2.50 - -5.92) \nonumber \\ \Delta &=& 6.84\nonumber \end{array} \label{2.10}\]
Si comparamos esto con una distribución χ 2 con un d.f., encontramos que P = 0.009. Debido a que este valor P es menor que el umbral de 0.05, rechazamos la hipótesis nula y apoyamos la alternativa. Concluimos que no se trata de una lagartija justa. Como cabría esperar, este resultado es consistente con nuestra respuesta de la prueba binomial en la sección anterior. Sin embargo, los enfoques son matemáticamente diferentes, por lo que los dos valores P no son idénticos.
Aunque se describió anteriormente en términos de dos hipótesis competitivas, las pruebas de relación de verosimilitud se pueden aplicar a situaciones más complejas con más de dos modelos competidores. Por ejemplo, si todos los modelos forman una secuencia de complejidad creciente, con cada modelo un caso especial del siguiente modelo más complejo, se puede comparar cada par de hipótesis en secuencia, deteniendo la primera vez que el estadístico de prueba no es significativo. Alternativamente, en algunos casos, las hipótesis se pueden colocar en un árbol de elección bifurcado, y se puede proceder de modelos simples a complejos por un camino particular de comparaciones emparejadas de modelos anidados. Este enfoque se utiliza comúnmente para seleccionar modelos de evolución de secuencias de ADN (Posada y Crandall 1998).
Sección 2.3c: El Criterio de Información Akaike (AIC)
Es posible que hayas notado que la prueba de razón de verosimilitud descrita anteriormente tiene algunas limitaciones. Especialmente para modelos que involucran más de un parámetro, los enfoques basados en pruebas de razón de verosimilitud solo pueden hacer mucho. Por ejemplo, se puede comparar una serie de modelos, algunos de los cuales están anidados dentro de otros, utilizando una serie ordenada de pruebas de relación de verosimilitud. Sin embargo, los resultados a menudo dependerán fuertemente del orden en que se lleven a cabo las pruebas. Además, a menudo queremos comparar modelos que no están anidados, como lo requieren las pruebas de cociente de verosimilitud. Por estas razones, otro enfoque, basado en el Criterio de Información Akaike (AIC), puede ser útil.
El valor AIC para un modelo particular es una función simple de la verosimilitud L y el número de parámetros k:
\[AIC = 2k − 2\ln L \label{2.11}\]
Esta función equilibra la probabilidad del modelo y el número de parámetros estimados en el proceso de ajuste del modelo a los datos. Se puede pensar en el criterio AIC como identificar el modelo que proporciona la manera más eficiente de describir patrones en los datos con pocos parámetros. Sin embargo, esta descripción abreviada de AIC no captura la justificación matemática y filosófica real de la ecuación (2.11). De hecho, esta ecuación no es arbitraria; en cambio, su compensación exacta entre los números de parámetros y la diferencia de verosimilitud logarítmica proviene de la teoría de la información (para más información, ver Burnham y Anderson 2003, Akaike (1998)).
La ecuación AIC (2.11) anterior sólo es válida para tamaños de muestra bastante grandes en relación con el número de parámetros que se estiman (para n muestras y k parámetros, n/k > 40). La mayoría de los conjuntos de datos empíricos incluyen menos de 40 puntos de datos independientes por parámetro, por lo que se debe emplear una pequeña corrección de tamaño de muestra:
\[ AIC_C = AIC + \frac{2k(k+1)}{n-k-1} \label{2.12}\]
Esta corrección penaliza a los modelos que tienen tamaños de muestra pequeños en relación con el número de parámetros; es decir, modelos donde hay casi tantos parámetros como puntos de datos. Como señalaron Burnham y Anderson (2003), esta corrección tiene poco efecto si los tamaños de muestra son grandes, por lo que proporciona una forma robusta de corregir posibles sesgos en conjuntos de datos de cualquier tamaño. Recomiendo usar siempre la corrección de tamaño de muestra pequeña al calcular los valores de AIC.
Para seleccionar entre los modelos, se pueden comparar sus puntuaciones A I C c y elegir el modelo con el menor valor. Es más fácil hacer comparaciones en puntuaciones A I C c entre modelos calculando la diferencia, Δ A I C c. Por ejemplo, si está comparando un conjunto de modelos, puede calcular Δ A I C c para el modelo i como:
\[ΔAIC_{c_i} = AIC_{c_i} − AIC_{c_{min}} \label{2.13}\]
donde A I C c i es la puntuación A I C c para el modelo i y A I C c m i n es la puntuación mínima A I C c en todos los modelos.
Como regla general general para comparar valores de A I C, cualquier modelo con un Δ A I C c i de menos de cuatro es aproximadamente equivalente al modelo con la A más baja I C c. valor. Los modelos con Δ A I C c i entre 4 y 8 tienen poco soporte en los datos, mientras que cualquier modelo con un Δ A I C c i mayor que 10 puede ser ignorado de manera segura.
Adicionalmente, se puede calcular el soporte relativo para cada modelo usando pesos Akaike. El peso para el modelo i en comparación con un conjunto de modelos de la competencia se calcula como:
\[ w_i = \frac{e^{-\Delta AIC_{c_i}/2}}{\sum_i{e^{-\Delta AIC_{c_i}/2}}} \label{2.14} \]
Los pesos para todos los modelos bajo consideración suman 1, por lo que el w i para cada modelo puede verse como una estimación del nivel de soporte para ese modelo en los datos en comparación con los otros modelos que se están considerando.
Volviendo a nuestro ejemplo de volteo de lagartos, podemos calcular las puntuaciones A I C c para nuestros dos modelos de la siguiente manera:
\[ \begin{array}{lcl} AIC_1 &=& 2 k_1 - 2 ln{L_1} = 2 \cdot 0 - 2 \cdot -5.92 \\\ AIC_1 &=& 11.8 \\\ AIC_2 &=& 2 k_2 - 2 ln{L_2} = 2 \cdot 1 - 2 \cdot -2.50 \\\ AIC_2 &=& 7.0 \\\ \end{array} \label{2.15} \]
Nuestro ejemplo es un poco inusual en ese modelo uno no tiene parámetros estimados; esto sucede a veces pero no es típico para aplicaciones biológicas. Podemos corregir estos valores para nuestro tamaño de muestra, que en este caso es n = 100 volteretas de lagarto:
\[ \begin{array}{lcl} AIC_{c_1} &=& AIC_1 + \frac{2 k_1 (k_1 + 1)}{n - k_1 - 1} \\\ AIC_{c_1} &=& 11.8 + \frac{2 \cdot 0 (0 + 1)}{100-0-1} \\\ AIC_{c_1} &=& 11.8 \\\ AIC_{c_2} &=& AIC_2 + \frac{2 k_2 (k_2 + 1)}{n - k_2 - 1} \\\ AIC_{c_2} &=& 7.0 + \frac{2 \cdot 1 (1 + 1)}{100-1-1} \\\ AIC_{c_2} &=& 7.0 \\\ \end{array} \label{2.16} \]
Observe que, en este caso particular, la corrección no afectó nuestros valores A I C, al menos a un decimal. Esto se debe a que el tamaño de la muestra es grande en relación con el número de parámetros. Tenga en cuenta que el modelo 2 tiene la puntuación A I C c más pequeña y, por lo tanto, es el modelo que mejor soporta los datos. Observando esto, ahora podemos convertir estas puntuaciones A I C c a una escala relativa:
\[ \begin{array}{lcl} \Delta AIC_{c_1} &=& AIC_{c_1}-AIC{c_{min}} \\\ &=& 11.8-7.0 \\\ &=& 4.8 \\\ \end{array} \label{2.17} \]
\[ \begin{array}{lcl} \Delta AIC_{c_2} &=& AIC_{c_2}-AIC{c_{min}} \\\ &=& 7.0-7.0 \\\ &=& 0 \\\ \end{array} \]
Obsérvese que el Δ A I C c i para el modelo 1 es mayor a cuatro, lo que sugiere que este modelo (el lagarto “justo”) tiene poco soporte en los datos. Esto vuelve a ser consistente con todos los resultados que hemos obtenido hasta ahora usando tanto la prueba binomial como la prueba de razón de verosimilitud. Finalmente, podemos usar las puntuaciones AICc relativas para calcular los pesos de Akaike:
\[ \begin{array}{lcl} \sum_i{e^{-\Delta_i/2}} &=& e^{-\Delta_1/2} + e^{-\Delta_2/2} \\\ &=& e^{-4.8/2} + e^{-0/2} \\\ &=& 0.09 + 1 \\\ &=& 1.09 \\\ \end{array} \label{2.18}\]
\[ \begin{array}{lcl} w_1 &=& \frac{e^{-\Delta AIC_{c_1}/2}}{\sum_i{e^{-\Delta AIC_{c_i}/2}}} \\\ &=& \frac{0.09}{1.09} \\\ &=& 0.08 \end{array} \]
\[ \begin{array}{lcl} w_2 &=& \frac{e^{-\Delta AIC_{c_2}/2}}{\sum_i{e^{-\Delta AIC_{c_i}/2}}} \\\ &=& \frac{1.00}{1.09} \\\ &=& 0.92 \end{array} \]
Nuestros resultados vuelven a ser consistentes con los resultados de la prueba de razón de verosimilitud. La probabilidad relativa de un lagarto injusto es de 0.92, y podemos estar bastante seguros de que nuestro lagarto no es un flipper justo.
Los pesos AIC también son útiles para otro propósito: podemos usarlos para obtener estimaciones de parámetros promediados por modelos. Estas son estimaciones de parámetros que se combinan en diferentes modelos proporcionales al soporte para esos modelos. Como ejemplo de pensamiento, imaginemos que estamos considerando dos modelos, A y B, para un conjunto de datos en particular. Tanto el modelo A como el modelo B tienen el mismo parámetro p, y este es el parámetro que nos interesa particularmente. En otras palabras, no sabemos qué modelo es el mejor modelo para nuestros datos, pero lo que realmente necesitamos es una buena estimación de p. Podemos hacer eso usando el promedio del modelo. Si el modelo A tiene un alto peso AIC, entonces la estimación del parámetro promediado por el modelo para p estará muy cerca de nuestra estimación de p bajo el modelo A; sin embargo, si ambos modelos tienen aproximadamente el mismo soporte, entonces la estimación del parámetro estará cerca del promedio de las dos estimaciones diferentes. El promedio de modelos puede ser muy útil en casos en los que existe mucha incertidumbre en la elección del modelo para modelos que comparten parámetros de interés. A veces los modelos en sí no son de interés, sino que necesitan ser considerados como posibilidades; en este caso, el promedio del modelo nos permite estimar parámetros de una manera que no es tan fuertemente dependiente de nuestra elección de modelos.


